Abstract
We consider Morawetz estimates for weighted energy decay of solutions to the wave equation on scattering manifolds (i.e., those with large conic ends). We show that a Morawetz estimate persists for solutions that are localized at low frequencies, independent of the geometry of the compact part of the manifold. We further prove a new type of Morawetz estimate in this context, with both hypotheses and conclusion localized inside the forward light cone. This result allows us to gain a \(1/2\) power of \(t\) decay relative to what would be dictated by energy estimates, in a small part of spacetime.

Similar content being viewed by others
Notes
We remark that in the body of the paper, \(X\) will refer to the manifold with boundary given by compactifying such a space.
We may a priori assume that \(h\) is in fact a smooth tensor including \(dr\) components; that we may then change variables to remove these components is a result of Joshi and Sá Barreto [9], Section 2.
If preferred, we could of course replace the norm on the inhomogeneity by the weighted \(L^2\) spacetime norm
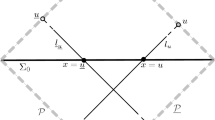
$$\begin{aligned}\int _0^T{\left||{(2+t^2)^{1/4} \log (2+t^2) (\Box +V) u}\right||}^2 \,dt.\end{aligned}$$The notation is short for “main face”, as for \(X\) Euclidean (diffeomorphically, not metrically), this can be identified with an open dense subset of the boundary of the radial compactification of Minkowski space. Note that the light cone, \(r/t=1\), hits the boundary in the interior of \(\mathrm mf \). If \(r/t=1\) in \(\mathrm mf \) were blown up inside \(\tilde{M}\), the resulting front face is where Friedlander’s radiation field [4] can be defined by rescaling a solution to the wave equation. Indeed, in the interior of this front face (in \(t>0\)) \(r-t=(r/t-1)/t^{-1}\) becomes a smooth variable along the fibers of the front face.
References
Bony, J.-F., Häfner, D.H.: The semilinear wave equation on asymptotically Euclidean manifolds. Commun. Partial Differ. Equ. 35(1), 23–67 (2010)
Bony, J.-F., Häfner, D.H.: Local energy decay for several evolution equations on asymptotically euclidean manifolds, arXiv:1008.2357
Bouclet, J.-M.: Low frequency estimates and local energy decay for asymptotically euclidean Laplacians. Commun. Partial Differ. Equ. 36(7), 1239–1286 (2011)
Friedlander, F.G.: Notes on the wave equation on asymptotically Euclidean manifolds. J. Funct. Anal. 184(1), 1–18 (2001)
Froese, R.G., Herbst, I.: A new proof of the Mourre estimate. Duke Math. J. 49, 1075–1085 (1982)
Guillarmou, C., Hassell, A., Sikora, A.: Resolvent at low energy III: the spectral measure. arXiv:1009.3084
Hassell, A., Vasy, A.: The spectral projections and the resolvent for scattering metrics. J. d’Analyse Math. 79, 241–298 (1999)
Hassell, A., Vasy, A.: The resolvent on Laplace-type operators on asymptotically conic spaces. Ann. Inst. Fourier 51, 1299–1346 (2001)
Joshi, Mark S.: Sá Barreto, Antônio Recovering asymptotics of metrics from fixed energy scattering data. Invent. Math. 137(1), 127–143 (1999)
Melrose, Richard B.: The Atiyah-Patodi-Singer index theorem, volume 4 of Research Notes in Mathematics. A K Peters Ltd., Wellesley, MA (1993)
Melrose, R.B.: Spectral and scattering theory for the Laplacian on asymptotically Euclidian spaces. In: Ikawa, M. (ed.) Spectral and scattering theory. Marcel Dekker, New York (1994)
Metcalfe, J., Tataru, D.: Global parametrices and dispersive estimates for variable coefficient wave equations. Math. Ann. (2012) (to appear)
Metcalfe, J., Tataru, D., Tohaneau, M.: Price’s law on nonstationary spacetimes, arXiv:1104.5437 (2011)
Morawetz, C.S.: The decay of solutions of the exterior initial-boundary value problem for the wave equation. Commun. Pure Appl. Math. 14, 561–568 (1961)
Morawetz, C.S., Ralston, J.V., Strauss, W.A.: Decay of solutions of the wave equation outside nontrapping obstacles. Commun. Pure Appl. Math. 30(4), 447–508 (1977)
Mourre, E.: Operateurs conjugés et propriétés de propagation. Commun. Math. Phys. 91, 279–300 (1983)
Perry, P., Sigal, I.M., Simon, B.: Spectral analysis of N-body Schrödinger operators. Ann. Math. 114, 519–567 (1981)
Ralston, J.V.: Solutions of the wave equation with localized energy. Commun. Pure Appl. Math. 22, 807–823 (1969)
Tataru, D.: Local decay of waves on asymptotically flat stationary space-times. Am. J. Math. (2012) (to appear)
Vainberg, B.R.: The short-wave asymptotic behavior of the solutions of stationary problems, and the asymptotic behavior as \(t\rightarrow \infty \) of the solutions of nonstationary problems. Uspehi Mat. Nauk 30, 2(182), 3–55 (1975) (Russian)
Vodev, G.: Local energy decay of solutions to the wave equation for nontrapping metrics. Ark. Mat. 42(2), 379–397 (2004)
Vasy, A., Wunsch, J.: Positive commutators at the bottom of the spectrum. J. Funct. Anal. 259(2), 503–523 (2010)
Author information
Authors and Affiliations
Corresponding author
Additional information
The authors gratefully acknowledge partial support from the NSF under grant numbers DMS-0801226 (A.V.) and DMS-0700318, DMS-1001463 (J.W.). A.V. is also grateful for support from a Chambers Fellowship at Stanford University. The authors are grateful to Daniel Tataru, and to an anonymous referee, for many helpful comments, and in particular for suggesting the refined \(\ell ^\infty \)–\(\ell ^1\) version of the estimates in Theorem 1.1.
Rights and permissions
About this article
Cite this article
Vasy, A., Wunsch, J. Morawetz estimates for the wave equation at low frequency. Math. Ann. 355, 1221–1254 (2013). https://doi.org/10.1007/s00208-012-0817-x
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00208-012-0817-x