Skip to main content
SpringerLink
Log in

Asymptotic Behaviour of a Pile-Up of Infinite Walls of Edge Dislocations

  • Published:
Archive for Rational Mechanics and Analysis Aims and scope Submit manuscript

Abstract

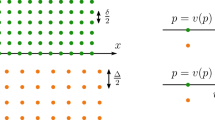
We consider a system of parallel straight edge dislocations and we analyse its asymptotic behaviour in the limit of many dislocations. The dislocations are represented by points in a plane, and they are arranged in vertical walls; each wall is free to move in the horizontal direction. The system is described by a discrete energy depending on the one-dimensional horizontal positions x i > 0 of the n walls; the energy contains contributions from repulsive pairwise interactions between all walls, a global shear stress forcing the walls to the left, and a pinned wall at x = 0 that prevents the walls from leaving through the left boundary. We study the behaviour of the energy as the number of walls, n, tends to infinity, and characterise this behaviour in terms of Γ-convergence. There are five different cases, depending on the asymptotic behaviour of the single dimensionless parameter β n , corresponding to \({\beta_n \ll 1/n, 1/n \ll \beta_n \ll 1}\), and \({\beta_n \gg 1}\), and the two critical regimes β n ~ 1/n and β n ~ 1. As a consequence we obtain characterisations of the limiting behaviour of stationary states in each of these five regimes. The results shed new light on the open problem of upscaling large numbers of dislocations. We show how various existing upscaled models arise as special cases of the theorems of this paper. The wide variety of behaviour suggests that upscaled models should incorporate more information than just dislocation densities. This additional information is encoded in the limit of the dimensionless parameter β n .

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alicandro R., Cicalese M.: A general integral representation result for continuum limits of discrete energies with superlinear growth. SIAM J. Math. Anal. 36(1), 1–37 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  2. Alicandro R., Cicalese M., Ponsiglione M.: Variational equivalence between Ginzburg–Landau, XY spin systems and screw dislocation energies. Indiana Univ. Math. J. 60, 171–208 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  3. Ambrosio, L., Fusco, N., Pallara, D.: Functions of Bounded Variation and Free Discontinuity Problems. Oxford Mathematical Monographs, 1st edn. Oxford University Press, 2000

  4. Ambrosio, L., Gigli, N., Savaré, G.: Gradient flows in metric spaces and in the space of probability measures. Lectures in mathematics ETH Birkhäuser, Zürich (2005)

  5. Asaro R.J., Rice J.R.: Strain localization in ductile single crystals. J. Mech. Phys. Solids 25, 309–338 (1977)

    Article  ADS  MATH  Google Scholar 

  6. Baskaran R., Sreekanth A., Mesarovic S., Zbib H.M.: Energies and distributions of dislocations in stacked pile-ups. Int. J. Solids Struc. 47, 1144–1153 (2010)

    Article  MATH  Google Scholar 

  7. Billingsley P.: Convergence of Probability Measures. Wiley-Interscience, New York (1999)

    Book  MATH  Google Scholar 

  8. Blake A., Zisserman A.: Visual Reconstruction. The MIT Press, Cambridge (1987)

    Google Scholar 

  9. Braides A., Cicalese M.: Surface energies in nonconvex discrete systems. Math. Models Methods Appl. Sci. 17, 985–1037 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  10. Braides A., Dal Maso G., Garroni A.: Variational formulation of softening phenomena in fracture mechanics: the one-dimensional case. Arch. Rational Mech. Anal. 146, 23–58 (1999)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  11. Braides A., Gelli M.S.: Continuum limits of discrete systems without convexity hypotheses. Math. Mech. Solids 7(1), 41–66 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  12. Braides, A., Gelli, M.S.: From discrete systems to continuous variational problems: an introduction. Topics on Concentration Phenomena and Problems with Multiple Scales, pp. 3–77, 2006

  13. Braides A., Lew A., Ortiz M.: Effective cohesive behavior of layers of interatomic planes. Arch. Rational Mech. Anal. 180, 151–182 (2006)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  14. Dal Maso G.: An Introduction to Γ-Convergence. Birkhäuser, Baasel (1993)

    Book  Google Scholar 

  15. Geus, de T.W.J., Peerlings R.H.J., Hirschberger C.B.: An analysis of the pile-up of infinite walls of edge dislocations (2013, submitted)

  16. Deng, J., El-Azab, A.: Mathematical and computational modelling of correlations in dislocation dynamics. Model. Simul. Mater. Sci. Eng. 17(2009)

  17. El-Azab A.: Statistical mechanics treatment of the evolution of dislocation distributions in single crystals. Phys. Rev. B 61(18), 11956–11966 (2000)

    Article  ADS  Google Scholar 

  18. Eshelby J.D., Frank F.C., Nabarro F.R.N.: The equilibrium of linear arrays of dislocations. Philos. Mag. 43, 351–364 (1951)

    MathSciNet  Google Scholar 

  19. Evers L.P., Brekelmans W.A.M., Geers M.G.D.: Scale dependent crystal plasticity framework with dislocation density and grain boundary effects. Int. J. Solids Struct. 41, 5209–5230 (2004)

    Article  MATH  Google Scholar 

  20. Fleck N.A., Muller G.M., Ashby M.F., Hutchinson J.W.: Strain gradient plasticity: theory and experiment. Acta Metall. Mater. 42(2), 475–487 (1994)

    Article  Google Scholar 

  21. Groma I.: Link between the microscopic and mesoscopic length-scale description of the collective behavior of dislocations. Phys. Rev. B 56(10), 5807–5813 (1997)

    Article  ADS  Google Scholar 

  22. Groma I., Balogh P.: Investigation of dislocation pattern formation in a two-dimensional self-consistent field approximation. Acta Mater. 47(13), 3647–3654 (1999)

    Article  Google Scholar 

  23. Groma I., Csikor F.F., Zaiser M.: Spatial correlation and higher-order gradient terms in a continuum description of dislocation dynamics. Acta Mater. 51, 1271–1281 (2003)

    Article  Google Scholar 

  24. Hall, C.L.: Asymptotic analysis of a pile-up of edge dislocation walls. Math. Sci. Eng. A Struct. (2013, to appear)

  25. Hall, E.O.: The deformation and ageing of mild steel: III. Discussion of results. Proc. Phys. Soc. Sect. B 64 (1951)

  26. Head A.K., Louat N.: The distribution of dislocations in linear arrays. Aust. J. Phys. 8(1), 1–7 (1955)

    MathSciNet  ADS  MATH  Google Scholar 

  27. Hill R.: Generalized constitutive relations for incremental deformation of metal crystals by multislip. J. Mech. Phys. Solids 14, 95–102 (1966)

    Article  ADS  Google Scholar 

  28. Hill, R., Havner, K.S.: Perspectives in the mechanics of elastoplastic crystals. J. Mech. Phys. Solids 30(5) (1982)

  29. Hill R., Rice J.R.: Constitutive analysis of elastic-plastic crystals at arbitrary strain. J. Mech. Phys. Solids 20, 401–413 (1972)

    Article  ADS  MATH  Google Scholar 

  30. Hull D., Bacon D.J.: Introduction to Dislocations. Butterworth-Heinemann, Oxford (2001)

    Google Scholar 

  31. Limkumnerd, S., Van der Giessen, E.: Statistical approach to dislocation dynamics: From dislocation correlations to a multiple-slip continuum theory of plasticity. Phys. Rev. B 77(18) (2008)

  32. McCann R.J.: A convexity principle for interacting gases. Adv. Math. 128, 153–179 (1997)

    Article  MathSciNet  MATH  Google Scholar 

  33. Mesarovic S., Baskaran R., Panchenko A.: Thermodynamic coarsening of dislocation mechanics and the size-dependent continuum crystal plasticity. J. Mech. Phys. Solids 58(3), 311–329 (2010)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  34. Petch N.J.: The cleavage strength of polycrystals. J. Iron Steel Institute 174(1), 25–28 (1953)

    Google Scholar 

  35. Roy A., Acharya A.: Size effects and idealized dislocation microstructure at small scales: prediction of a phenomenological model of Mesoscopic Field Dislocation Mechanics. Part II. J. Mech. Phys. Solids 54(8), 1711–1743 (2006)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  36. Roy A., Peerlings R.H.J., Geers M.G.D., Kasyanyuk Y.: Continnum modeling of dislocation interactions: why discreteness matters? Math. Sci. Eng. A Struct. 486, 653–661 (2008)

    Article  Google Scholar 

  37. Scardia, L., Peerlings, R.H.J., Peletier, M.A., Geers, M.G.D.: Mechanics of dislocation pile-ups: a unification of scaling regimes (2013, submitted)

  38. Sandier E., Serfaty S.: Gamma-convergence of gradient flows with applications to Ginzburg–Landau. Commun. Pure Appl. Math. 57(12), 1627–1672 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  39. Sandier, E., Serfaty, S.: From the Ginzburg–Landau model to vortex lattice problems. Arxiv preprint arXiv:1011.4617 (2010)

    Google Scholar 

  40. Zaiser, M., Miguel, M.C., Groma, I.: Statistical dynamics of dislocation systems: the influence of dislocation-dislocation correlations. Phys. Rev. B 64(22) (2001)

Download references

Author information

Author notes

  1. L. Scardia

    Present address: School of Mathematics and Statistics, University of Glasgow, Glasgow, UK

Authors and Affiliations

  1. Department of Mechanical Engineering, Technische Universiteit Eindhoven, Eindhoven, The Netherlands

    M. G. D. Geers & R. H. J. Peerlings

  2. Department of Mathematics and Computer Sciences, Institute for Complex Molecular Systems, Technische Universiteit Eindhoven, Eindhoven, The Netherlands

    M. A. Peletier

Authors
  1. M. G. D. Geers
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. R. H. J. Peerlings
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. M. A. Peletier
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. L. Scardia
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to L. Scardia.

Additional information

Communicated by S. Müller

Until 2012 L. Scardia was in the Department of Mechanical Engineering and the Department of Mathematics and Computer Science at the Technische Universiteit Eindhoven, The Netherlands, supported by the Materials innovation institute (M2i).

Rights and permissions

Reprints and permissions

About this article

Cite this article

Geers, M.G.D., Peerlings, R.H.J., Peletier, M.A. et al. Asymptotic Behaviour of a Pile-Up of Infinite Walls of Edge Dislocations. Arch Rational Mech Anal 209, 495–539 (2013). https://doi.org/10.1007/s00205-013-0635-7

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00205-013-0635-7

Keywords

Search

Navigation