Skip to main content
SpringerLink
Log in

Estimating a restricted normal mean

  • Published:
Metrika Aims and scope Submit manuscript

Abstract

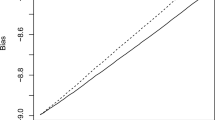
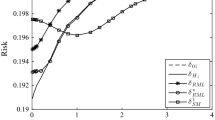
Let X 1, X 2, ..., X n be a random sample from a normal distribution with unknown mean μ and known variance σ 2. In many practical situations, μ is known a priori to be restricted to a bounded interval, say [−m, m] for some m > 0. The sample mean \(\bar{X}\) , then, becomes an inadmissible estimator for μ. It is also not minimax with respect to the squared error loss function. Minimax and other estimators for this problem have been studied by Casella and Strawderman (Ann Stat 9:870–878, 1981), Bickel (Ann Stat 9:1301–1309, 1981) and Gatsonis et al. (Stat Prob Lett 6:21–30, 1987) etc. In this paper, we obtain some new estimators for μ. The case when the variance σ 2 is unknown is also studied and various estimators for μ are proposed. Risk performance of all estimators is numerically compared for both the cases when σ 2 may be known and unknown.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Bader G, Bischoff W (2003) Old and new aspects of minimax estimation of a bounded parameter. Mathematical Statistics and Applications, Festschrift for Constance van Eeden, IMS Lecture notes-monograph series, vol 42, pp 15–30

  2. Bickel PJ (1981). Minimax estimation of the mean of a normal distribution when the parameter is restricted. Ann Stat 9: 1301–1309

    Article  MATH  MathSciNet  Google Scholar 

  3. Casella G and Strawderman WE (1981). Estimating a bounded normal mean. Ann Stat 9: 870–878

    Article  MATH  MathSciNet  Google Scholar 

  4. Gatsonis C, MacGibbon B and Strawderman WE (1987). On the estimation of a restricted normal mean. Stat Prob Lett 6: 21–30

    Article  MATH  MathSciNet  Google Scholar 

  5. Ghosh MN (1964). Uniform approximation of minimax point estimates. Ann Math Stat 35: 1031–1047

    Article  MATH  Google Scholar 

  6. Ghosh M (1974). Admissibility and minimaxity of some maximum likelihood estimators when the parameter space is restricted to integers. J R Stat Soc Ser B 37: 264–271

    Google Scholar 

  7. Ghosh M and Meeden G (1978). Admissibility of the MLE of the normal integer mean. Sankhya B 40: 1–10

    MATH  MathSciNet  Google Scholar 

  8. Gupta AK and Rohatgi VK (1980). On the estimation of restricted mean. J Stat Plan Infer 4: 369–379

    Article  MATH  MathSciNet  Google Scholar 

  9. Hammersley JM (1950). On estimating restricted parameters. J R Stat Soc Ser B 12: 192–229

    MathSciNet  Google Scholar 

  10. Heiny RL and Siddiqui MM (1970). Estimation of the parameters of a normal distribution when the mean is restricted to a interval. Aus J Stat 12: 112–117

    Article  MATH  Google Scholar 

  11. Katz MW (1961). Admissible and minimax estimates of parameters in truncated spaces. Ann Math Stat 32: 136–142

    Article  MATH  Google Scholar 

  12. Kempthorne PJ (1987). Numerical specification of discrete least favorable prior distributions. SIAM J Sci Stat Comput 8: 178–184

    MathSciNet  Google Scholar 

  13. Khan RA (1973). On some properties of Hammersley’s estimator of an integer mean. Ann Stat 1: 838–850

    Article  MATH  Google Scholar 

  14. Kumar S and Sharma D (1992). An inadmissibility result for affine equivariant estimators. Stat Dec 10: 87–97

    MATH  MathSciNet  Google Scholar 

  15. Lehmann EL and Casella G (1998). Theory of point estimation, 2nd edn. Springer, New York

    MATH  Google Scholar 

  16. Marchand É, Strawderman WE (2004) Estimation in restricted parameter spaces: a review. Festschrift for Herman Rubin, IMS lecture notes-monograph series, pp 21–44

  17. Moors JJA (1981). Inadmissibility of linearly invariant estimators in truncated parameter spaces. J Am Stat Assoc 76: 910–915

    Article  MATH  MathSciNet  Google Scholar 

  18. Moors JJA (1985) Estimation in truncated parameter spaces. Ph.D. Thesis. Tilburg University, The Netherlands

  19. Shao PYi-S and Strawderman WE (1996). Improving on the MLE of a positive normal mean. Stat Sin 6: 259–274

    MATH  MathSciNet  Google Scholar 

  20. Sinha SK (1998). Bayesian estimation. New Age International (P) Ltd, New Delhi

    Google Scholar 

  21. Stein C (1981). Estimation of the mean of a multivariate normal distribution. Ann Stat 9: 1135–1151

    Article  MATH  Google Scholar 

  22. Stroud TWF (1974). Combining unbiased estimates of a parameter known to be positive. J Am Stat Assoc 69: 502–506

    Article  MATH  MathSciNet  Google Scholar 

  23. Tripathi YM and Kumar S (2007). Estimating a positive normal mean. Stat Pap 48: 609–629

    Article  MATH  MathSciNet  Google Scholar 

  24. van Eeden C (1996). Estimation in restricted parameter spaces - some history and some recent developments. CWI Q 9: 69–76

    MATH  Google Scholar 

  25. van Eeden C (2006) Restricted parameter space estimation problems: admissibility and minimaxity properties. Lecture Notes in Statistics 188. Springer, New York

Download references

Author information

Authors and Affiliations

  1. Department of Mathematics, Indian Institute of Technology Kharagpur, Kharagpur, 721 302, India

    Somesh Kumar & Yogesh Mani Tripathi

Authors
  1. Somesh Kumar
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Yogesh Mani Tripathi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Somesh Kumar.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Kumar, S., Tripathi, Y.M. Estimating a restricted normal mean. Metrika 68, 271–288 (2008). https://doi.org/10.1007/s00184-007-0157-0

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00184-007-0157-0

Keywords

Search

Navigation