Skip to main content
SpringerLink
Log in

A mixed problem of plane elasticity theory for a multiply connected domain with partially unknown boundary: the case of a rhombus

  • Published:
Zeitschrift für angewandte Mathematik und Physik Aims and scope Submit manuscript

Abstract

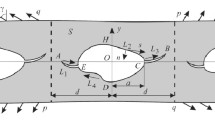
This paper addresses a problem of plane elasticity theory for a multiply connected domain, whose external boundary is a rhombus and the internal boundary is the required two holes that are symmetric with respect to its diagonals. Absolutely rigid punches with rectilinear bases are applied to each segment of the outer boundary of the given body, and they are under the action of the forces P that apply to their middle points. There is no friction between the surface of the given elastic body and the punches. The boundaries of the unknown holes are free from external loads. Tangential stresses are equal to zero along the entire boundary of the domain, and the normal displacements on the linear parts of the boundary are constant. The shapes of the holes’ contours and the stress state of the given body are determined, provided that the tangential normal stress arising at the holes’ contours takes a constant value. Such holes are called full-strength holes. Full-strength contours and stress state are found by means of complex analysis. The solution is written in quadratures. Numerical analyses are presented, and the corresponding plots are constructed.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Banichuk N.V.: Optimality conditions in the problem of seeking the hole shapes in elastic bodies. J. Appl. Math. Mech. 41(5), 920–925 (1977)

    Article  MathSciNet  Google Scholar 

  2. Banichuk N.V.: Optimization of Forms of Elastic Bodies. Nauka, Moscow (1980)

    MATH  Google Scholar 

  3. Bantsuri R.: On one mixed problem of the plane theory of elasticity with a partially unknown boundary. Proc. A. Razmadze Math. Inst. 140, 9–16 (2006)

    MathSciNet  MATH  Google Scholar 

  4. Bantsuri R.: Solution of the mixed problem of plate bending for a multi-connected domain with partially unknown boundary in the presence of cyclic symmetry. Proc. A. Razmadze Math. Inst. 145, 9–22 (2007)

    MathSciNet  MATH  Google Scholar 

  5. Bantsuri R., Mzhavanadze S.: The mixed problem of the theory of elasticity for a rectangle weakened by unknown equi-strong holes. Proc. A. Razmadze Math. Inst. 145, 23–33 (2007)

    MathSciNet  MATH  Google Scholar 

  6. Bantsuri, R.D.: Some inverse problems of plane elasticity and of bending of thin plates. In: Continuum Mechanics and Related Problems of Analysis, pp. 100–107. Metsniereba, Tbilisi (1993)

  7. Bantsuri R.D., Isakhanov R.S.: Some inverse problems in elasticity theory. Trudy Tbiliss. Mat.Inst. Razmadze Akad. Nauk Gruzin. SSR 87, 3–20 (1987)

    MathSciNet  MATH  Google Scholar 

  8. Cherepanov G.P.: Inverse problems of the plane theory of elasticity. J. Appl. Math. Mech. 38(6), 915–931 (1975)

    Article  MathSciNet  Google Scholar 

  9. Keldysh, M., Sedov, L.: The effective solution of some boundary problems for harmonic functions. Dokl. Akad. Nauk SSSR 16(1), 7–10 (1937). Russian

  10. Muskhelishvili, N.I.: Some Basic problems of mathematical theory of elasticity. Nauka, Moscow (1966). Russian

  11. Muskhelishvili N.I.: Singular Integral Equations. Dover Publications Inc, New York (1992)

    Google Scholar 

  12. Neuber, H.: The optimization of stresses concentration. In: Continuum Mechanics and Related Problems of Analysis, pp. 375–380. Nauka, Moscow (1972)

  13. Odishelidze N.: Solution of the mixed problem of the plane theory of elasticity for a multiply connected domain with partially unknown boundary in the presence of axial symmetry. Proc. A. Razmadze Math. Inst. 146, 97–112 (2008)

    MathSciNet  MATH  Google Scholar 

  14. Odishelidze N., Criado-Aldeanueva F.: A mixed problem of plane elasticity for a domain with a partially unknown boundary. Int. Appl. Mechan. 42(3), 342–349 (2006)

    Article  MathSciNet  Google Scholar 

  15. Odishelidze N., Criado-Aldeanueva F.: Some axially symmetric problems of the theory of plane elasticity with partially unknown boundaries. Acta Mech. 199, 227–240 (2008)

    Article  MATH  Google Scholar 

  16. Odishelidze N., Criado-Aldeanueva F.: A mixed problem of plate bending for a doubly connected domains with partially unknown boundary in the presence of cycle symmetry. Sci. China Phys. Mech. Astron. 53(10), 1884–1894 (2010)

    Article  Google Scholar 

  17. Odishelidze N., Criado-Aldeanueva F., Criado F., Sanchez J.: Solution of one mixed problem of plate bending for a domain with partially unknown boundary. Acta Mechan. 219(1-2), 169–179 (2011)

    Article  MATH  Google Scholar 

  18. Odishelidze N., Criado-Aldeanueva F., Criado F., Sanchez J.: On one contact problem of plane elasticity for a doubly connected domain: application to a hexagon. Zeitschrift fr Angewandte Mathematik und Physik 64(1), 193–200 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  19. Odishelidze N., Criado-Aldeanueva F., Sanchez J.: A mixed problem of plate bending for a regular octagon weakened with a required full-strength hole. Acta Mechan. 224(1), 183–192 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  20. Vigdergauz S.B.: On a case of the inverse problem of the two-dimensional theory of elasticity. J. Appl. Math. Mech. 41(5), 902–908 (1977)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Interdisciplinary Department (Mathematics, Computer Sciences), Faculty of Exact and Natural Sciences, Iv. Javakhishvili Tbilisi State University, Tbilisi, Georgia

    Nana Odishelidze

  2. Department of Applied Physics II, Polytechnic School, Malaga University, Campus El Ejido, Málaga, Spain

    Francisco Criado-Aldeanueva

  3. Department of Statistics and Operational Research, Faculty of Sciences, Malaga University, Campus Teatinos, Málaga, Spain

    J. M. Sanchez

Authors
  1. Nana Odishelidze
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Francisco Criado-Aldeanueva
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. J. M. Sanchez
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Francisco Criado-Aldeanueva.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Odishelidze, N., Criado-Aldeanueva, F. & Sanchez, J.M. A mixed problem of plane elasticity theory for a multiply connected domain with partially unknown boundary: the case of a rhombus. Z. Angew. Math. Phys. 66, 2899–2907 (2015). https://doi.org/10.1007/s00033-015-0546-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00033-015-0546-6

Mathematics Subject Classification

Keywords

Search

Navigation