Skip to main content
SpringerLink
Log in

Hyper-ideal Circle Patterns with Cone Singularities

  • Published:
Results in Mathematics Aims and scope Submit manuscript

Abstract

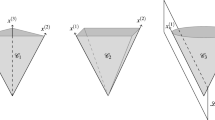
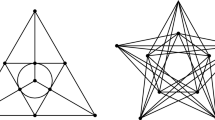
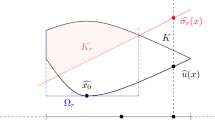
The main objective of this study is to explore how hyper-ideal circle patterns can be reconstructed from given combinatorial angle data. More precisely, we focus on the existence, uniqueness and construction of hyper-ideal circle patterns with prescribed combinatorics and intersection angles between adjacent circles. In essence, we propose a new proof of the already existing results from Jean-Marc Schlenker’s work on the topic. Our attempt is to develop a slightly different approach that is potentially more suitable for applications and thus leading to a more direct convex variational principle than Schlenker’s.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Alexandrov A.D.: Convex Polyhedra. Springer, Berlin (2002)

    Google Scholar 

  2. Andreev E.M.: On convex polyhedra in Lobacevskii space. Math. USSR Sb. 10, 413–440 (1970)

    Article  Google Scholar 

  3. Andreev E.M.: On convex polyhedra of finite volume in Lobacevskii space. Math. USSR Sb. 12, 255–259 (1970)

    Article  Google Scholar 

  4. Bao X., Bonahon F.: Hyperideal polyhedra in hyperbolic 3-space. Bull. Soc. Math. Fr. 130(3), 457–491 (2002)

    MATH  MathSciNet  Google Scholar 

  5. Benedetti R., Petronio C.: Lectures on Hyperbolic Geometry. Universitext, Springer, Berlin (1992)

    Book  MATH  Google Scholar 

  6. Bobenko A.I., Izmestiev I.: Alexandrov’s theorem, weighted Delaunay triangulations, and mixed volumes. Ann. Inst. Fourier 58(2), 447–505 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  7. Bobenko A.I., Springborn B.A.: Variational principles for circle patterns and Koebe’s theorem. Trans. Am. Math. Soc. 356(2), 659–689 (2004)

    Article  MATH  MathSciNet  Google Scholar 

  8. Buser P.: Geometry and Spectra of Compact Riemann Surfaces, Progress in Math. 106. Birkhäuser, Boston (1992)

    Google Scholar 

  9. Colin de Verdière, Y.: Un principe variationnel pour les empilements de cercles.. Invent. Math. 104(3), 655–669 (1991)

  10. Dimitrov, N.: Hyper-ideal circle patterns with cone singularities, extended electronic version. arXiv:math.MG/14066741

  11. Edelsbrunner H.: Geometry and Topology for Mesh Generation, Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, Cambridge (2001)

    Book  Google Scholar 

  12. Leibon G.: Characterizing the Delaunay decompositions of compact hyperbolic surfaces. Geom. Topol. 6, 361–391 (2002)

    Article  MATH  MathSciNet  Google Scholar 

  13. Milnor, J.W.: The Schläfli differential equality. In: Collected Papers I: Geometry, pp. 281–295. Publish or Perish, Houston (1994)

  14. Rivin I.: Euclidean structures of simplicial surfaces and hyperbolic volume. Ann. Math. 139, 553–580 (1994)

    Article  MATH  MathSciNet  Google Scholar 

  15. Rivin I.: A characterization of ideal polyhedra in hyperbolic 3-space. Ann. Math. 2 143(1), 51–70 (1996)

    Article  MATH  MathSciNet  Google Scholar 

  16. Rivin I.: Combinatorial optimization in geometry. Adv. Appl. Math. 31(1), 242–271 (2003)

    Article  MATH  MathSciNet  Google Scholar 

  17. Roeder R.K.W., Hubbard J.H., Dunbar W.D.: Andreev’s theorem on hyperbolic polyhedra. Ann. Inst. Fourier 57(3), 825–882 (2007)

    Article  MATH  MathSciNet  Google Scholar 

  18. Rousset M.: Sur la rigidité de polyèdres hyperboliques en dimension 3: cas de volume fini, cas hyperidéal cas fuchsien. Bull. Soc. Math. Fr. 132(2), 233–261 (2004)

    MATH  MathSciNet  Google Scholar 

  19. Schläfli, L.: Theorie der vielfachen Kontinuität, Gesammelte Math. Abh. 1. Birkhäuser, Basel, pp. 167–392 (1950)

  20. Schlenker J.-M.: Hyperideal circle patterns. Math. Res. Lett. 12(1), 85–112 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  21. Schlenker J.-M.: Circle patterns on singular surfaces. Discrete Comput. Geom. 40(1), 47–102 (2008)

    Article  MATH  MathSciNet  Google Scholar 

  22. Schlenker, J.-M.: Hyperideal polyhedra in hyperbolic manifolds, electronic version. arXiv:math.GT/0212355

  23. Schlenker J.-M.: A rigidity criterion for non-convex polyhedra. Discrete Comput. Geom. 33(2), 207–221 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  24. Springborn B.A.: A variational principle for weighted Delaunay triangulations and hyperideal polyhedra. J. Differ. Geom. 78(2), 333–367 (2008)

    MATH  MathSciNet  Google Scholar 

  25. Springborn B.A.: A unique representation of polyhedral types. Centering via Möbius transformations. Math. Z. 249(3), 513–517 (2005)

    Article  MATH  MathSciNet  Google Scholar 

  26. Thurston, W.P.: The geometry and topology of three-manifolds, Electronic library of MSRI (2002). http://library.msri.org/books/gt3m/

  27. Thurston, W.P.: Three-dimensional geometry and topology. In: Levy, S. (ed.) Princeton Mathematical Series, vol. 35. Princeton University Press, Princeton (1997)

  28. Ushijima A.: A volume formula for generalized hyperbolic tetrahedra. Non-Euclidean Geom. 581, 249–265 (2006)

    Article  MathSciNet  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Insitut für Mathematik MA 8-4, Technische Universität Berlin, Straße des 17. Juni 136, 10623, Berlin, Germany

    Nikolay Dimitrov

Authors
  1. Nikolay Dimitrov
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Nikolay Dimitrov.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Dimitrov, N. Hyper-ideal Circle Patterns with Cone Singularities. Results. Math. 68, 455–499 (2015). https://doi.org/10.1007/s00025-015-0453-3

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00025-015-0453-3

Mathematics Subject Classification

Keywords

Search

Navigation