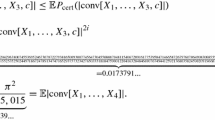Abstract
We prove that there exists an absolute constant \({\alpha > 1}\) with the following property: if K is a convex body in \({{\mathbb R}^n}\) whose center of mass is at the origin, then a random subset \({X\subset K}\) of cardinality \({{\rm card}(X)=\lceil\alpha n\rceil }\) satisfies with probability greater than \({1-e^{-c_1n}}\)
where \({c_1, c_2 > 0}\) are absolute constants. As an application we show that the vertex index of any convex body K in \({{\mathbb R}^n}\) is bounded by \({c_3n^2}\), where \({c_3 > 0}\) is an absolute constant, thus extending an estimate of Bezdek and Litvak for the symmetric case.
Similar content being viewed by others
References
S. Artstein-Avidan, A. Giannopoulos, and V. D. Milman, Asymptotic Geometric Analysis, Part I, Mathematical Surveys and Monographs 202, Amer. Math. Soc., Providence, RI, 2015.
Ball K. M., Pajor A.: Convex bodies with few faces. Proc. Amer. Math. Soc. 110, 225–231 (1990)
A. Barvinok, Thrifty approximations of convex bodies by polytopes, Int. Math. Res. Not. IMRN (2014), 4341–4356.
J. Batson, D. Spielman, and N. Srivastava, Twice-Ramanujan Sparsifiers, STOC’ 2009: Proceedings of the 41st annual ACM Symposium on Theory of Computing, ACM, New York, 2009, pp. 255–262.
Bezdek K.: The illumination conjecture and its extensions. Period. Math. Hungar. 53, 59–69 (2006)
Bezdek K., Litvak A.E.: On the vertex index of convex bodies. Adv. Math. 215, 626–641 (2007)
J. Bourgain, On the distribution of polynomials on high dimensional convex sets, in Geom. Aspects of Funct. Analysis, Lecture Notes in Mathematics 1469, Springer, Berlin, 1991, 127–137.
S. Brazitikos, Quantitative Helly-type theorem for the diameter of convex sets, Preprint (arXiv:1511.07779).
S. Brazitikos, A. Giannopoulos, P. Valettas, and B-H. Vritsiou, Geometry of isotropic convex bodies, Mathematical Surveys and Monographs 196, American Mathematical Society, Providence, RI, 2014.
Dafnis N., Giannopoulos A., Tsolomitis A.: Asymptotic shape of a random polytope in a convex body. J. Funct. Anal. 257, 2820–2839 (2009)
Giannopoulos A., Milman V. D.: Concentration property on probability spaces. Adv. Math. 156, 77–106 (2000)
Gluskin E. D., Litvak A. E.: Asymmetry of convex polytopes and vertex index of symmetric convex bodies. Discrete Comput. Geom. 40, 528–536 (2008)
E. D. Gluskin and A. E. Litvak, A remark on vertex index of the convex bodies, in Geom. Aspects of Funct. Analysis, Lecture Notes in Math. 2050, Springer, Berlin, 2012, 255–265.
Guédon O., Milman E.: Interpolating thin-shell and sharp large-deviation estimates for isotropic log-concave measures. Geom. Funct. Anal. 21, 1043–1068 (2011)
Haberl C.: \({L_p}\) intersection bodies. Adv. Math. 217, 2599–2624 (2008)
F. John, Studies and Essays Presented to R. Courant on his 60th Birthday, January 8, 1948, 187–204. Interscience Publishers, Inc., New York, N. Y., 1948.
Kannan R., Lovász L., Simonovits M.: Isoperimetric problems for convex bodies and a localization lemma. Discrete Comput. Geom. 13, 541–559 (1995)
Klartag B.: On convex perturbations with a bounded isotropic constant. Geom. Funct. Anal. 16, 1274–1290 (2006)
Klartag B., Milman E.: Centroid bodies and the logarithmic Laplace transform—a unified approach, J. Funct. Anal. 262 (2012), 10–34.
Lutwak E., Yang D., Zhang G.: \({L^p}\) affine isoperimetric inequalities. J. Differential Geom. 56, 111–132 (2000)
V. D. Milman and A. Pajor, Isotropic position and inertia ellipsoids and zonoids of the unit ball of a normed n-dimensional space, in Geom. Aspects of Funct. Analysis, Lecture Notes in Mathematics 1376, Springer, Berlin, 1989, 64–104.
Paouris G.: Concentration of mass in convex bodies. Geom. Funct. Anal. 16, 1021–1049 (2006)
Paouris G.: Small ball probability estimates for log-concave measures. Trans. Amer. Math. Soc. 364, 287–308 (2012)
Paouris G., Werner E.: Relative entropy of cone measures and \({L_p}\)-centroid bodies. Proc. Lond. Math. Soc. 104, 253–286 (2012)
R. Schneider, Convex Bodies: The Brunn-Minkowski Theory, Second expanded edition. Encyclopedia of Mathematics and Its Applications 151, Cambridge University Press, Cambridge, 2014.
N. Srivastava, On contact points of convex bodies, in Geom. Aspects of Funct. Analysis, Lecture Notes in Mathematics 2050, Springer, Berlin, 2012, 393–412.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Brazitikos, S., Chasapis, G. & Hioni, L. Random approximation and the vertex index of convex bodies. Arch. Math. 108, 209–221 (2017). https://doi.org/10.1007/s00013-016-0975-2
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00013-016-0975-2