The secant condition for instability in biochemical feedback control—II. Models with upper hessenberg jacobian matrices

Abstract

We consider ann-component biochemical system whose Jacobian matrixJ is of upper Hessenberg form, with principal subdiagonal elementsb ₁,b ₂, ...,b _n−1 and upper right-hand corner element −f. The open-loop Jacobian matrixJ ₀ is formed fromJ by settingf=0. It is shown that if the characteristic roots of −J ₀ are real and non-negative then a necessary condition for instability at a critical point (steady state) is

$$\frac{{b_1 b_2 ...b_{n - 1} f}}{{\left| { - J_0 } \right|}} \geqslant (\sec \pi /n)^n $$

This condition is analyzed in terms of reaction orders. For a metabolic sequence with some reversible steps, no loss of intermediate metabolites, and competitive inhibition of the first enzyme by the last metabolite, the above necessary condition becomes

$$\frac{{\beta _{N - 1} X_{n + 1} }}{{\xi _{N - 1} E_{0T} }} \geqslant (\sec \pi /N)^N $$

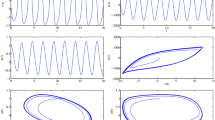
whereN is the number of components (metabolites, enzyme-substrate complexes, and enzyme-inhibitor complex),β _N-1 the order of the enzyme-inhibitor reaction (with respect to the inhibitor),ξ _N-1 the order of reaction for the removal of the last metabolite, andX _n+1 /E _0T the fraction of first enzyme blocked by inhibitor. It is shown that, under certain assumptions, a critical point is always stable in a single two-step enzymatic process (formation of enzyme-substrate complex, followed by conversion to product, then loss of product) with slow negative feedback by competitive product inhibition. A model is constructed showing that stable oscillations can occur in a feedback system with only two metabolic steps and negative feedback by competitive inhibition with no cooperativity. The instability is due to a slow feedback reaction and saturable removal of the second metabolite.