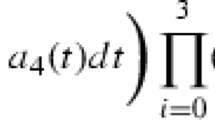Abstract
In this paper we consider the stability property of single-species patches connected by diffusion with a within-patch dynamics of Volterra type and with continuous time delays. We prove that this system can only have two kinds of equilibria: the positive and the trivial one. By the assumption that the delay kernels are convex combinations of suitable non-negative and normalized functions, the linear chain trick gives an expanded system of O.D.E. with the same stability properties as the original integro-differential system. Homotopy function techniques provide sufficient conditions for the existence of the positive equilibrium and for its global stability. We also prove the local stability of any positive equilibrium and the local instability both of positive and trivial equilibria. The biological meanings of the results obtained are compared with known results from the literature.
Similar content being viewed by others
Literature
Beretta, E. and F. Solimano. 1985. “A Generalization of Integro-differential Volterra Models in Population Dynamics: Boundedness and Global Asymptotic Stability.” To apper inSIAM J. appl. Math.
Beretta, E. and Y. Takeuchi. 1986. “Global Asymptotic Stability of Lotka-Volterra Diffusion Models with Continuous Time Delay.” To appear inSIAM J. appl. Math.
Berman, A. and R. J. Plemmons. 1979.Non-negative Matrices in the Mathematical Sciences. New York: Academic Press.
Cushing, J. M. 1977.Integro-differential Equations and Delay Models in Population Dynamics.Lect. Notes in Biomath. 20. Berlin: Springer.
D'Ancona, U. 1954.The Struggle for Existence. Leiden, Netherlands: E. J. Brill.
Freedman, H. I., B. Rai and P. Waltman. 1986. “Mathematical Models of Population Interactions with Dispersal—II. Differential Survival in a Change of Habitat.”J. math. Anal. Applic. 115, 140–154.
Garcia, C. B. and W. I. Zangwill. 1981.Pathways to Solutions, Fixed Points and Equilibria. Englewood Cliffs, NJ: Prentice-Hall.
Hastings, A. 1978. “Global Stability in Lotka-Volterra Systems with Diffusion.”J. math. Biol. 6, 163–168.
—. 1982. “Dynamics of a Single Species in a Spatially Varying Environment: The Stabilizing Role of Higher Dispersal Rates.”J. math. Biol. 16, 49–55.
Holt, R. D. 1985. “Population Dynamics in Two-patch Environments: Some Anomalous Consequences of an Optimal Habitat Distribution.”Theor. Pop. Biol. 28, 181–208.
Levin, S. A. 1974. “Dispersion and Population Interactions.”Am. Nat. 108, 207–228.
—. 1976. “Spatial Partitioning and the Structure of Ecological Communities.” InSome Mathematical Questions in Biology, Vol. VII. Providence, RI: American Mathematical Society.
— and L. A. Segel. 1976. “Hypothesis to Explain the Origin of Planktonic Patchness.”Nature, Lond. 259, 659.
MacDonald, N. 1978.Time Lags in Biological Models.Lect. Notes in Biomath. 27. Berlin: Springer.
Miller, R. K. 1966. “On Volterra's Population Equation.”SIAM J. appl. Math. 14, 446–452.
Okubo, A. 1980.Diffusion and Ecological Problems: Mathematical Models. Berlin: Springer.
Pozio, M. A. 1984. “Conditions for Global Asymptotic Stability of Equilibria in Some Models with Delay.”Atti del 40 Simposio di Dinamica di Popolazioni (Parma 22–24 Ottobre 1981), pp. 271–275.
Scudo, F. M. and J. R. Ziegler. 1978.The Golden Age of Theoretical Ecology: 1923–1940Lect. Notes in Biomath. 22. Berlin: Springer.
Skellam, J. G. 1951. “Random Dispersal in Theoretical Populations.”Biometrika 38, 196–218.
Solimano, F. and E. Beretta. 1983. “Existence of a Globally Asymptotically Stable Equilibrium in Volterra Models with Continuous Time Delay.”J. math. Biol. 18, 93–102.
Takeuchi, Y. 1986. “Global Stability in Generalized Lotka-Volterra Diffusion Models.”J. math. Anal. Applic. 116, 209–221.
—. 1987. “Diffusion Effect on Stability of Lotka-Volterra Models.”Bull. math. Biol. 48, 585–601.
Vance, R. R. 1984. “The Effect of Dispersal on Population Stability in One Species, Discrete-Space Population Growth Models.”Am. Nat. 123, 230–254.
Author information
Authors and Affiliations
Additional information
This work was performed under the auspices of G.N.F.M., C.N.R. (Italy) and within the activity of the Evolution Equations and Applications group, M.P.I. (Italy).
I thank the Department of Applied Mathematics, Shizuoka University, Japan, which enabled me to visit Urbino.
Rights and permissions
About this article
Cite this article
Beretta, E., Takeuchi, Y. Global stability of single-species diffusion volterra models with continuous time delays. Bltn Mathcal Biology 49, 431–448 (1987). https://doi.org/10.1007/BF02458861
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF02458861