Abstract
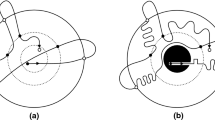
We prove theorems pertaining to periodic arrays of spherical, obstacles which show how the macroscopic limit of the mean free path depends on the scaling of the size of the obstacles. We treat separately the cases where the obstacles are totally and partially absorbing, and we also distinguish between two-dimensional arrays, where our results are optimal, and higher dimensional arrays, where they are not. The cubically symmetric arrays to which these results apply do not have finite horizon.
This is a preview of subscription content, log in via an institution to check access.
Similar content being viewed by others
References
R. Alexandre and K. Hamdache, Homogénéisation d'équations cinétiques en milieu perforé,C. R. Acad. Sci. 313:339–344 (1991).
V. I. Arnold,Geometrical Methods in the Theory of Ordinary Differential Equations (Springer-Verlag, New York, 1983).
C. Boldigrini, L. A. Bunimovich, and Ya. G. Sinai, On the Boltzmann Equation for the Lorentz gas,J. Stat. Phys. 32(3):477–501 (1983).
L. A. Bunimovich and Ya. G. Sinai, Markov partitions of dispersed billiards.,Commun. Math. Phys. 73:247–280 (1980); Statistical properties of the Lorentz gas with periodic configurations of scatterers,Commun. Math. Phys. 78:479–497 (1981).
L. A. Bunimovich, Ya. G. Sinai, and N. I. Chernov, Markov partitions for two-dimensional hyperbolic billiards,Russ. Math. Surv. 45(3):105–152 (1990); Statistical properties of two-dimensional hyperbolic billiards,Russ. Math. Surv. 46(4):47–106 (1991).
J. W. S. Cassels,An Introduction to Diophantine Approximation (Cambridge University Press, Cambridge, 1957).
M. Cessenat, Théorèmes de traceL p pour les espaces de fonctions de la neutronique,C.R. Acad. Sci. 300:89–92 (1985).
H. S. Dumas, Ergodization rates for linear flow on the torus,J. Dynam. Diff. Equations 3:593–610 (1991).
G. Gallavotti, Rigorous theory of the Boltzmann equation in the Lorentz gas, Nota Interna No. 358, Istituto di Fisica, Università di Roma (1972).
F. Golse, Transport dans les milieux composites fortement contrastés I: Le modèle du billard,Ann. Inst. Henri Poincaré 61:381–410 (1994).
R. Illner and M. Pulvirenti, Global validity of the Boltzmann equation for a two-dimensional rare gas in a vacuum,Commun. Math. Phys. 105:189–203 (1986).
O. E. Lanford III, Time evolution of large classical systems, inDynamical Systems, Theory and Applications J. Moser, ed. (Springer-Verlag, New York, 1975), pp. 1–111.
M. Pulvirenti, Global validity of the Boltzmann equation for a three-dimensional rare gas in a vacuum,Commun. Math. Phys. 113:79–85 (1987).
W. M. Schmidt,Diophantine Approximation (Springer-Verlag, Berlin, 1980).
L. Schwartz,Théorie des distributions (Hermann, Paris, 1966).
H. Spohn, The Lorentz flight process converges to a random flight process,Commun. Math. Phys. 60:277–290 (1978).
P. Bleher, Statistical properties of two-dimensional periodic Lorentz gas with infinite horizon,J. Stat. Phys. 66:315–373 (1992).
J. Bourgain, F. Golse, and B. Wennberg, In preparation.
L. A. Bunimovich, Decay of correlations in dynamical systems with chaotic behavior,Sov. Phys. JETP 62:842–852 (1985).
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
Dumas, H.S., Dumas, L. & Golse, F. On the mean free path for a periodic array of spherical obstacles. J Stat Phys 82, 1385–1407 (1996). https://doi.org/10.1007/BF02183388
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF02183388