Abstract
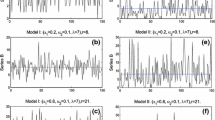
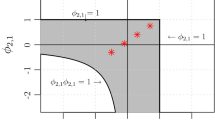
Threshold autoregressive (AR) and autoregressive moving average (ARMA) processes with continuous time parameter have been discussed in several recent papers by Brockwellet al. (1991,Statist. Sinica,1, 401–410), Tong and Yeung (1991,Statist. Sinica,1, 411–430), Brockwell and Hyndman (1992,International Journal Forecasting,8, 157–173) and Brockwell (1994,J. Statist. Plann. Inference,39, 291–304). A threshold ARMA process with boundary width 2δ>0 is easy to define in terms of the unique strong solution of a stochastic differential equation whose coefficients are piecewise linear and Lipschitz. The positive boundary-width is a convenient mathematical device to smooth out the coefficient changes at the boundary and hence to ensure the existence and uniqueness of the strong solution of the stochastic differential equation from which the process is derived. In this paper we give a direct definition of a threshold ARMA processes with δ=0 in the important case when only the autoregressive coefficients change with the level of the process. (This of course includes all threshold AR processes with constant scale parameter.) The idea is to express the distributions of the process in terms of the weak solution of a certain stochastic differential equation. It is shown that the joint distributions of this solution with δ=0 are the weak limits as δ ↓ 0 of the distributions of the solution with δ>0. The sense in which the approximating sequence of processes used by Brockwell and Hyndman (1992,International Journal Forecasting,8, 157–173) converges to this weak solution is also investigated. Some numerical examples illustrate the value of the latter approximation in comparison with the more direct representation of the process obtained from the Cameron-Martin-Girsanov formula. It is used in particular to fit continuous-time threshold models to the sunspot and Canadian lynx series.
Similar content being viewed by others
References
Billingsley, P. (1986).Probability, 2nd ed., Springer, New York.
Brockwell, P. J. (1994). On continuous time threshold ARMA processes,J. Statist. Plann. Inference,39, 291–304.
Brockwell, P. J. and Davis, R. A. (1991).Time Series: Theory and Methods, 2nd ed., Springer, New York.
Brockwell, P. J. and Hyndman, R. J. (1992). On continuous time threshold autoregression,International Journal Forecasting,8, 157–173.
Brockwell, P. J., Hyndman, R. J. and Grunwald, G. K. (1991). Continuous time threshold autoregressive models,Statist. Sinica,1, 401–410.
Gikhman, I. I. and Skorokhod, A. V. (1969).Introduction to the Theory of Random Processes, W. B. Saunders, Philadelphia.
Granger, C. W. and Andersen, A. P. (1978).An Introduction to Bilinear Time Series Models, Vanderhoek and Ruprecht, Göttingen.
Ichihara, K. and Kunita, H. (1974). A classification of the second order degenerate elliptic operators and its probabilistic characterization,Zeit. Wahrscheinlichkeitsth.,30, 235–254.
Jones, R. H. (1981). Fitting a continuous time autoregression to discrete data,Applied Time Series Analysis II (ed. D. F. Findley), 651–682, Academic Press, New York.
Jones, R. H. and Ackerson, L. M. (1990). Serial correlation in unequally spaced longitudinal data,Biometrika,77, 721–732.
Karatzas, I. and Shreve, S. E. (1991).Brownian Motion and Stochastic Calculus, Springer, New York.
Kushner, H. J. (1984).Approximation and Weak Convergence Methods for Random Processes, The MIT Press, Cambridge, Massachusetts.
Nicholls, D. F. and Quinn, B. G. (1982). Random coefficient autoregressive models: an introduction,Lecture Notes in Statist.,11, Springer, New York.
Oksendal, B. (1989).Stochastic Differential Equations, 2nd ed., Springer, Berlin.
Petruccelli, J. D. (1990). A comparison of tests for SETAR-type non-linearity in time series,International Journal of Forecasting,6, 25–36.
Stroock, D. W. and Varadhan, S. R. S. (1979).Multidimensional Diffusion Processes, Springer, Berlin.
Subba-Rao T. and Gabr, M. M. (1984). An introduction to bispectral analysis and bilinear time series models,Lecture Notes in Statist.,24, Springer, New York.
Tong, H. (1983). Threshold models in non-linear time series analysis,Lecture Notes in Statist.,21, Springer, New York.
Tong, H. (1990).Non-linear Time Series: A Dynamical System Approach, Clarendon Press, Oxford.
Tong, H. and Yeung, I. (1991). Threshold autoregressive modelling in continuous time,Statist. Sinica,1, 411–430.
Tsay, R. S. (1989). Testing and modeling threshold autoregressive processes,J. Amer. Statist. Assoc.,84, 231–240.
Author information
Authors and Affiliations
Additional information
Research partially supported by National Science Foundation Research Grants DMS 9105745 and 9243648.
About this article
Cite this article
Brockwell, P.J., Stramer, O. On the approximation of continuous time threshold ARMA processes. Ann Inst Stat Math 47, 1–20 (1995). https://doi.org/10.1007/BF00773408
Received:
Revised:
Issue Date:
DOI: https://doi.org/10.1007/BF00773408