Summary
In the absence of detailed knowledge of how the CNS controls a muscle through its motor fibers, a reasonable hypothesis is that of optimal control. This hypothesis is studied using a simplified mathematical model of a single muscle, based on A. V. Hill's equations, with series elastic element omitted, and with the motor signal represented by a single input variable.
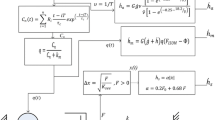
Two cost functions were used. The first was total energy expended by the muscle (work plus heat). If the load is a constant force, with no inertia, Hill's optimal velocity of shortening results. If the load includes a mass, analysis by optimal control theory shows that the motor signal to the muscle consists of three phases: (1) maximal stimulation to accelerate the mass to the optimal velocity as quickly as possible, (2) an intermediate level of stimulation to hold the velocity at its optimal value, once reached, and (3) zero stimulation, to permit the mass to slow down, as quickly as possible, to zero velocity at the specified distance shortened. If the latter distance is too small, or the mass too large, the optimal velocity is not reached, and phase (2) is absent. For lengthening, there is no optimal velocity; there are only two phases, zero stimulation followed by maximal stimulation.
The second cost function was total time. The optimal control for shortening consists of only phases (1) and (3) above, and is identical to the minimal energy control whenever phase (2) is absent from the latter.
Generalization of this model to include viscous loads and a series elastic element are discussed.
Similar content being viewed by others
References
Abbott, B. C., Bigland, B., Ritchie, J. M.: The physiological cost of negative work. J. Physiol. 117, 380–390 (1952).
Athans, M., Falb, P. L.: Optimal Control. New York: McGraw-Hill 1966.
Ayoub, M. A., Ayoub, M. M., Walkevar, A. G.: A biomechanical model for the upper extremity using optimization techniques. Human Factors 16, 585–594 (1974).
Basmajian, J. V.: Muscles Alive. Their Functions Revealed by Electromyography. Baltimore: Williams and Wilkins 1962.
Beckett, R., Chang, K.: An evaluation of the kinematics of gait by minimum energy, pp. 15–26 in: Biomechanics (Bootzin, D., Muffley, H. C., eds.). New York: Plenum 1969.
Bigland, B., Lippold, O. C. J.: The relation between force, velocity and integrated electrical activity in human muscles. J. Physiol. 123, 214–224 (1954).
Chow, C. K., Jacobson, D. H.: Studies of human locomotion via optimal programming. Math. Biosci. 10, 239–306 (1971).
Close, J. R.: Motor Functions in the Lower Extremities. Analyses by Electronic Instrumentation. Springfield: Ch. C Thomas 1964.
Cohn, D. L.: Optimal systems: I. The vascular system. Bull. Math. Biophys. 16, 59–74 (1954).
Halze, H.: Optimization of human motions, pp 138–143 in Medicine and Sport (Cerquilini, S., Venerando, A., Wartenweiler, J., eds.). Vol. 8. Biomechaanics III. Basel: Karger 1973.
Hill, A. V.: The heat of shortening and the dynamic constants of muscle. Proc. Roy. Soc. B 126, 262–274 (1938).
Hill, A. V.: The mechanical efficiency of frog's muscle. Proc. Roy. Soc. B 127, 434–451 (1939).
Hill, A. V.: The dynamic constants of human muscle. Proc. Roy. Soc. B 128, 262–274 (1940).
Hill, A. V.: Production and absorption of work by muscle. Science 131, 897–903 (1960).
Hill, A. V.: The effect of load on the heat of shortening of muscle. Proc. Roy. Soc. B 159, 297–318 (1964a).
Hill, A. V.: The efficiency of mechanical power development during muscular shortening and its relation to load. Proc. Roy. Soc. B 159, 319–324 (1964b).
Hill, A. V., Howarth, J. V.: The reversal of chemical reactions in contracting muscle during an applied stretch. Proc. Roy. Soc. B 151, 169–193 (1959).
Hopf, H. C., Handwerker, H., Hausmanns, J.: Die rasche Willkürbewegung des Menschen. Deutsche Zeitschr. f. Nervenheilkunde 191, 186–209 (1967).
Huxley, A. F., Simmons, R. M.: Proposed mechanism of force generation in striated muscle. Nature 233, 533–538 (1971).
Joyce, G. C., Rack, P. M. H., Westbury, D. R.: Some mechanical properties of the cat soleus muscle at various stimulus rates. J. Physiol. 197, 23P-25P (1968).
Katz, B.: The relation between force and speed in muscular contraction. J. Physiol. 96, 45–64 (1939).
Leitman, G.: An Introduction to Optimal Control. New York: McGraw-Hill 1966.
Matthews, P. B. C.: Mammalian Muscle Receptors and Their Central Actions. Baltimore: Williams and Wilkins 1972.
Merriam, C. W. III.: Optimization Theory and the Design of Feedback Control Systems. New York: McGraw-Hill 1964.
Nubar, Y., Contini, R.: A minimal principle in biomechanics. Bull. Math. Biophys. 23, 377–391 (1961).
Pfeiffer, A.: Ein kybernetisches Gütemaß für die Koordinierung von Bewegungen. Z. f. Psychol. 171, 395–399 (1965).
Pini, A.: Relazione forza-velocita nel muscolo umano in vivo nel lavoro motore e resistente. Boll. Soc. Ital. Biol. Sper. 41, 1548–1550 (1965).
Pontryagin, L. S., Boltyanskii, V. G., Gamkrelidze, R. V., Mishchenko, E. F.: The Mathematical Theory of Optimal Processes. New York: Interscience 1962.
Ralston, H. J.: Recent advances in neuromuscular physiology. Am J. Physical Medicine 36, 94–120 (1957).
Rashevsky, N.: Mathematical Biophysics, 3rd ed., Vol. 2, p. 292. New York: Dover 1960.
Rosen, R.: Optimality Principles in Biology. New York: Plenum 1967.
Wacholder, K.: Willkürliche Haltung und Bewegung, insbesondere im Lichte elektrophysiologischer Untersuchungen. Ergebnisse der Physiologie 26, 568–775 (1928).
Wacholder, K.: Die Arbeitsfähigkeit des Menschen in ihrer Abhängigkeit von der Funktionsweise des Muskel- und Nervensystems, pp. 587–642, in: Handbuch der normalen und pathologischen Physiologie (Bethe, A., et al., eds.), Band 15, 1. Hälfte. 1930.
Author information
Authors and Affiliations
Rights and permissions
About this article
Cite this article
FitzHugh, R. A model of optimal voluntary muscular control. J. Math. Biology 4, 203–236 (1977). https://doi.org/10.1007/BF00280973
Received:
Issue Date:
DOI: https://doi.org/10.1007/BF00280973