Abstract
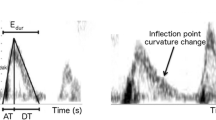
The mechanical suction-pump feature of the left ventricle aspirates atrial blood and generates a rapid rise and fall in transmitral flow (Doppler E-wave). Initially, E-wave deceleration time (DT), a routine index of clinical diastolic function, was thought to be determined only by chamber stiffness. Kinematic modeling of filling, in analogy to damped oscillatory motion [Parametrized Diastolic Filling (PDF) formalism], has been extensively validated and accurately predicts clinically observed E-wave contours while, revealing that DT is actually an algebraic function of both stiffness (PDF parameter k) and relaxation (PDF parameter c). We hypothesize that kinematic modeling based E-wave analysis accurately predicts the stiffness (DTs) and relaxation (DTr) components of DT such that DT = DTs + DTr. For validation, pressure–volume (P–V) and E-wave data from 12 control (DT < 220 ms) and 12 delayed-relaxation (DT > 220 ms) subjects, 738 beats total, were analyzed. For each E-wave, DTs and DTr was compared to simultaneous, gold-standard, high fidelity (Millar catheter) determined, chamber stiffness (K = ΔP/ΔV) and chamber relaxation (time-constant of isovolumic relaxation—τ), respectively. For the group linear regression yielded DTs = α K + β (R = 0.82) with α = −0.38 and β = 0.20, and DTr = m τ + b (R = 0.94) with m = 2.88 and b = −0.12. We conclude that PDF-based E-wave analysis provides the DTs and DTr components of DT with simultaneous chamber stiffness (K) and relaxation (τ) respectively, as primary determinants. This kinematic modeling based method of E-wave analysis is immediately translatable clinically and can assess the effects of pathology and pharmacotherapy as causal determinants of DT.






Similar content being viewed by others
Abbreviations
- AT:
-
E-wave acceleration time (ms)
- DF:
-
Diastolic function
- DR:
-
Delayed relaxation
- DT:
-
E-wave deceleration time (ms)
- DTr :
-
Relaxation component of DT (ms)
- DTs :
-
Stiffness component of DT (ms)
- E dur :
-
E-wave duration
- IVR:
-
Isovolumic relaxation
- IVRT:
-
Isovolumic relaxation time (ms)
- K :
-
Diastatic stiffness (mmHg/mL)
- LV:
-
Left ventricle/ventricular
- LVEDV:
-
Left ventricular end diastolic volume (mL)
- LVEF:
-
Left ventricular ejection fraction
- LVEDP:
-
Left ventricular end diastolic pressure (mmHg)
- NR:
-
Normal relaxation
- PDF:
-
Parametrized Diastolic Filling
- P–V :
-
Pressure–volume
- τ :
-
Time constant of isovolumic relaxation (ms)
References
Bauman, L., C. S. Chung, M. Karamanoglu, and S. J. Kovács. The peak atrioventricular pressure gradient to transmitral flow relation: kinematic model prediction with in vivo validation. J. Am. Soc. Echocardiogr. 17:839–844, 2004.
Boskovski, M., L. Shmuylovich, and S. J. Kovács. Transmitral flow velocity-contour variation after premature ventricular contractions: a novel test of the load-independent index of diastolic filling. Ultrasound Med. Biol. 34(12):1901–1908, 2008.
Chung, C. S., D. M. Ajo, and S. J. Kovács. Isovolumic pressure-to-early rapid filling decay rate relation: model-based derivation and validation via simultaneous catheterization echocardiography. J. Appl. Physiol. 100:528–534, 2006.
Chung, C. S., M. Karamanoglu, and S. J. Kovács. Duration of diastole and its phases as a function of heart rate during spine bicycle exercise. Am. J. Physiol. Heart Circ. Physiol. 287:H2003–H2008, 2004.
Chung, C. S., and S. J. Kovács. Physical determination of left ventricular isovolumic pressure decline: model prediction with in vivo validation. Am. J. Physiol. 294:H1589–H1596, 2008.
Courtois, M., S. J. Kovács, and P. A. Ludbrook. Transmitral pressure–flow velocity relation. Importance of regional pressure gradients in the left ventricle during diastole. Circulation 78:661–671, 1988.
Dent, C. L., A. W. Bowman, M. J. Scott, J. S. Allen, J. B. Lisauskas, M. Janif, S. A. Wickline, and S. J. Kovács. Echocardiographic characterization of fundamental mechanisms of abnormal diastolic filling in diabetic rats with a parameterized diastolic filling formalism. J. Am. Soc. Echocardiogr. 14(12):1166–1172, 2001.
Eucker, S. A., J. B. Lisuaskas, J. Singh, and S. J. Kovács. Phase plane analysis of left ventricular hemodynamics. J. Appl. Physiol. 90:2238–2244, 2001.
Feigenbaum, H. Echocardiography. Baltimore, MD: Williams & Wilkins, p. 677, 1993.
Flachskampf, F. A., A. E. Weyman, J. L. Guerrero, and J. D. Thomas. Calculation of atrioventricular compliance from the mitral flow profile: analytic and in vitro study. J. Am. Coll. Cardiol. 19:998–1004, 1992.
Garcia, M. J., M. S. Firstenberg, N. L. Greenberg, N. Smedira, L. Rodriguez, D. Prior, and J. D. Thomas. Estimation of left ventricular operating stiffness from Doppler early filling deceleration time in humans. Am. J. Physiol. Heart Circ. Physiol. 280:H554–H561, 2001.
Garcia, M. J., J. D. Thomas, and A. L. Klein. New Doppler echocardiographic applications for the study of diastolic function. J. Am. Coll. Cardiol. 32:865–875, 1998.
Hall, A. F., and S. J. Kovács. Automated method for characterization of diastolic transmitral Doppler velocity contours: early rapid filling. Ultrasound Med. Biol. 20:107–116, 1994.
Ishida, Y., J. Meisner, K. Tsujioka, J. Gallo, C. Yoran, R. Frater, and E. Yellin. Left ventricular filling dynamics: influence of left ventricular relaxation and left atrial pressure. Circulation 74:187–196, 1986.
Kass, D. A., J. G. F. Bronzwaer, and W. J. Paulus. What mechanism underline diastolic dysfunction in heart failure? Circ. Res. 94:1533–1542, 2004.
Kovács, S. J., B. Barzilai, and J. E. Pérez. Evaluation of diastolic function with Doppler echocardiography: the PDF formalism. Am. J. Physiol. 87:H178–H187, 1987.
Kovács, S. J., M. D. McQueen, and C. S. Peskin. Modeling cardiac fluid dynamics and diastolic function. Philos. Trans. R. Soc. A 359:1299–1314, 2001.
Kovács, S. J., J. S. Meisner, and E. L. Yellin. Modeling of diastole. Cardiol. Clin. 18:459–487, 2000.
Kovács, S. J., R. Setser, and A. F. Hall. Left ventricular chamber stiffness from model-based image processing of transmitral Doppler E-waves. Coron. Artery Dis. 8:179–187, 1997.
Lee, D. S., P. Gona, R. S. Vasan, M. G. Larson, E. J. Benjamin, T. J. Wang, J. V. Tu, and D. Levy. Relation of disease pathogenesis and risk factors to heart failure with preserved or reduced ejection fraction: insights from the Framingham heart study of the national heart, lung, and blood institute. Circulation 119:3070–3077, 2009.
Lisauskas, J. B., J. Singh, A. W. Bowman, and S. J. Kovács. Chamber properties from transmitral flow: prediction of average and passive left ventricular diastolic stiffness. J. Appl. Physiol. 91:154–162, 2001.
Lisauskas, J. B., J. Singh, M. Courtois, and S. J. Kovács. The relation of the peak Doppler E-wave to peak mitral annulus velocity ratio to diastolic function. Ultrasound Med. Biol. 27:499–507, 2001.
Little, W. C., M. Ohno, D. W. Kitzman, J. D. Thomas, and C. P. Cheng. Determination of left ventricular chamber stiffness from the time for deceleration of early left ventricular filling. Circulation 92:1933–1939, 1995.
Maeder, M. T., and D. M. Kaye. Heart failure with normal left ventricular ejection fraction. J. Am. Coll. Cardiol. 53:905–918, 2009.
Marino, P., W. C. Little, A. Rossi, E. Barbieri, M. Anselmi, G. Destro, A. Prioli, L. Lanzoni, and P. Zardini. Can left ventricular diastolic stiffness be measured noninvasively? J. Am. Soc. Echocardiogr. 15:935–943, 2002.
Miki, S., T. Murakami, T. Iwase, T. Tomita, Y. Nakamura, and C. Kawai. Doppler echocardiographic transmitral peak early velocity does not directly reflect hemodynamic changes in humans. J. Am. Coll. Cardiol. 17:1507–1516, 1991.
Mossahebi, S., and S. J. Kovács. Kinematic modeling-based left ventricular diastatic (passive) chamber stiffness determination with in-vivo validation. Ann. BME. 40(5):987–995, 2012.
Mossahebi, S., L. Shmuylovich, and S. J. Kovács. The thermodynamics of diastole: kinematic modeling based derivation of the P–V loop to transmitral flow energy relation, with in vivo validation. Am. J. Physiol. Heart Circ. Physiol. 300:H514–H521, 2011.
Murakami, T., O. Hess, J. Gage, J. Grimm, and H. Krayenbuehl. Diastolic filling dynamics in patients with aortic stenosis. Circulation 73:1162–1174, 1986.
Nagueh, S. F., C. P. Appleton, T. C. Gillebert, P. N. Marino, J. K. Oh, O. A. Smiseth, A. D. Waggoner, F. A. Flachskampf, P. A. Pellikka, and A. Evangelista. Recommendations for the evaluation of left ventricular diastolic function by echocardiography. J. Am. Soc. Echocardiogr. 22(2):107–133, 2009.
Nikolic, S. D., E. L. Yellin, K. Tamura, H. Vetter, T. Tamura, J. S. Meisner, and R. W. Frater. Passive properties of canine left ventricle: diastolic stiffness and restoring forces. Circ. Res. 62:1210–1222, 1988.
Oh, J. K., C. P. Appleton, L. K. Hatle, R. A. Nishimura, J. B. Seward, and J. Tajik. The noninvasive assessment of left ventricular diastolic function with two-dimensional and Doppler echocardiography. J. Am. Soc. Echocardiogr. 10:246–270, 1997.
Ohte, N., S. Nakano, Y. Mizutani, T. Samoto, and T. Fujinami. Relation of mitral valve motion to left ventricular end-diastolic pressure assessed by M-mode echocardiography. J Cardiogr. 16(1):115–120, 1986.
Oki, T., T. Tabata, Y. Mishiro, H. Yamada, M. Abe, Y. Onose, T. Wakatsuki, A. Iuchi, and S. Ito. Pulsed tissue Doppler imaging of left ventricular systolic and diastolic wall motion velocities to evaluate differences between long and short axes in healthy subjects. J. Am. Soc. Echocardiogr. 12:308–313, 1999.
Omens, J., and Y. C. Fung. Residual strain in rat left ventricle. Circ. Res. 66:37–45, 1990.
Owan, T. E., D. O. Hodge, R. M. Herges, S. J. Jacobsen, V. L. Roger, and M. M. Redfield. Trends in prevalence and outcome of heart failure with preserved ejection fraction. N. Engl. J. Med. 355:251–259, 2006.
Riordan, M. M., C. S. Chung, and S. J. Kovács. Diabetes and diastolic function: stiffness and relaxation from transmitral Flow. Ultrasound Med. Biol. 31:1589–1596, 2005.
Shmuylovich, L., and S. J. Kovács. E-wave deceleration time may not provide an accurate determination of left ventricular chamber stiffness if left ventricular relaxation/viscoelasticity is unknown. Am. J. Physiol. Heart Circ. Physiol. 292:H2712–H2720, 2007.
Templeton, G. H., and L. R. Nardizzi. Elastic and viscous stiffness of the canine left ventricle. J. Appl. Physiol. 36:123–127, 1974.
Thomas, J. D., C. Y. P. Choong, F. A. Flachskampf, and A. E. Weyman. Analysis of the early transmitral Doppler velocity curve: effect of primary physiologic changes and compensatory preload adjustment. J. Am. Coll. Cardiol. 16:644–655, 1990.
Thomas, J. D., F. A. Flachskampf, C. Chen, J. L. Guerrero, M. H. Picard, R. A. Levine, and A. E. Weyman. Isovolumic relaxation time varies predictably with its time constant and aortic and left atrial pressure: implications for the noninvasive evaluation of ventricular relaxation. Am. Heart J. 124:1305–1313, 1992.
Thomas, J. D., J. B. Newell, C. Y. P. Choong, and A. E. Weyman. Physical and physiological determinants of transmitral velocity: numerical analysis. Am. J. Physiol. Heart Circ. Physiol. 260(23):H1718–H1730, 1991.
Weiss, J. L., J. W. Frederiksen, and M. L. Weisfeldt. Hemodynamic determinants of the time-course of fall in canine left ventricular pressure. J. Clin. Investig. 58(3):751–760, 1976.
Zhang, W., C. S. Chung, L. Shmuylovich, and S. J. Kovács. Viewpoint: is left ventricular volume during diastasis the real equilibrium volume and, what is its relationship to diastolic suction? J. Appl. Physiol. 105:1012–1014, 2008.
Zhang, W., and S. J. Kovács. The diastatic pressure–volume relationship is not the same as the end-diastolic pressure–volume relationship. Am. J. Physiol. Heart Circ. Physiol. 294(6):H2750–H2760, 2008.
Zhang, W., L. Shmuylovich, and S. J. Kovács. The E-wave delayed relaxation pattern to LV pressure contour relation: model-based prediction with in vivo validation. Ultrasound Med. Biol. 36:497–511, 2010.
Zile, M. R., C. F. Baicu, and W. H. Gaasch. Diastolic heart failure—abnormalities in active relaxation and passive stiffness of the left ventricle. N. Engl. J. Med. 350:1953–1959, 2004.
Zile, M. R., and D. L. Brutsaert. New concepts in diastolic dysfunction and diastolic heart failure: part I. Circulation 105:1387–1393, 2002.
Acknowledgments
This work was supported in part by the Alan A. and Edith L Wolff Charitable Trust, St. Louis, and the Barnes-Jewish Hospital Foundation. Sina Mossahebi was supported in part by a teaching assistantship from the Physics Department, Washington University College of Arts and Sciences. We thank sonographer Peggy Brown for expert echocardiographic data acquisition, and the staff of Barnes Jewish Hospital Cardiovascular Procedure Center’s Cardiac Catheterization Laboratory for their assistance.
Conflict of interest
The authors have no conflicts of interest to disclose with the reported study.
Human Subjects
Prior to data acquisition, subjects provided signed, institutional review board (IRB) approved informed consent for participation in accordance with Washington University Human Research Protection Office (HRPO) criteria.
Animal Studies
This work did not include any animal studies.
Author information
Authors and Affiliations
Corresponding author
Additional information
Associate Editor Ajit P. Yoganathan oversaw the review of this article.
Appendix
Appendix
The PDF Formalism
The PDF formalism characterizes Doppler transmitral velocity profiles kinematically according to damped SHO motion.16 Thus transmitral blood flow velocity is the result of simultaneous elastic, inertial, and damping forces. The relative roles of these forces are reflected in the values of the three mathematically independent model-derived parameters: k, c, and x o. The SHO equation of motion for the E-wave is given by:
where the terms, from left to right, represent the inertial, resistive, and elastic forces, respectively and we calculate the parameters per unit mass. Without loss of generality the parameters k and c are computed on a per unit mass basis.16,18
Newton’s second law governs the process and solves the “inverse problem” of diastole by providing three unique parameters of k, c, and x o, for each E-wave contour.13 The solution of Eq. (A.1) yields E-wave velocity, given by:
where \( \omega = \sqrt {4k - c^{2} } /2, \) when 4k > c 2 underdamped kinematic regime characteristic of NR, and
where \( \beta = \sqrt {c^{2} - 4k} /2, \) when 4k < c 2 overdamped kinematic regime, characteristic of DR.
The three parameters c, k and x o encompass the (lumped) physiologic determinants of all E-wave contours. The initial oscillator displacement x o (cm) is linearly related to the velocity–time integral (VTI) of the E-wave.19 Chamber stiffness (dP/dV) is linearly related to the spring constant k (g/s2),19,21 while the chamber viscoelasticity/relaxation index c (g/s) characterizes the resistance of the process.18,19 E-waves with long concave up deceleration portions are fit by the overdamped solution and have higher c values, while E-waves that approximate nearly symmetric sine waves are fit by the underdamped solution and have lower c values.38
Parametrized Diastolic Filling parameter c, k, and x o values are determined via the Levenberg–Marquardt algorithm as a part of generating the fit to the E-wave maximum velocity envelope via a custom Lab VIEW (National Instruments, Austin, TX) interface.13 The algorithm provides parameter values and a simultaneous measure of goodness of fit.
Rights and permissions
About this article
Cite this article
Mossahebi, S., Kovács, S.J. Kinematic Modeling Based Decomposition of Transmitral Flow (Doppler E-Wave) Deceleration Time into Stiffness and Relaxation Components. Cardiovasc Eng Tech 5, 25–34 (2014). https://doi.org/10.1007/s13239-014-0176-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13239-014-0176-8