Introduction

Water mixed with earth and air is the main source from which people draw the goods for their life. Water resources are renewable and inexhaustible. Under the influence of solar energy, a part of Earth′s water is in constant traffic between the Earth′s surface and the atmosphere, which is known as the hydrologic cycle. However, the fact that the hydrological movement is not fortuned with an equable way can affect the torrential streams, sometimes even with harmful results. Heavy rainfall leads to an increased formation of runoff and flooding phenomena. In contrast, lack of rainfall minimizes runoff and causes water shortages and scarcity conditions (Paparrizos 2012).

When the streams flow from higher to lower areas, the water drags, carries and deposits various materials which distracts from the crust leading them through a declining surface resulting in aggradations in the lowlands. Corrosive action that is created from water transformation consists one of the major geo-morphological factors which creates serious problems in humans (Potouridis 2009).

It is easy to understand that the water problem and its disastrous consequences is a critical issue for the less developing countries and for the more developed. Nowadays, the assessment, prevention, preparedness, response and restoration of a hydro-meteorological event with any of the consequences are integrated risk management effort. It is understood that prior reduction of risks and losses is a less expensive solution than the subsequent rehabilitation and reconstruction (Anderson 1991).

In the Greek surface several water problems occurred in the recent years, mainly due to the uneven spatial and temporal distribution of water resources, the uneven spatial and temporal distribution of water demand, the existence of trans-boundary rivers in northern Greece and many Greek Islands that are facing semi-arid conditions. Increased consumption, reduced water flow from neighboring countries, pollution and persistence of extreme events (droughts, floods) contribute to the lack of water resources availability (Paparrizos and Chatziminiadis 2010).

Sperchios River basin is an area where the agricultural activity is the main production and economic activity. According to data from the Hellenic Statistical Authority (2009), the region of Ftiotida has a total population of 169,542 inhabitants from which, 52,426 (30.9 %) are employed fully or partly in the primary sector (agriculture and livestock). Due to this fact, most of the local population uses the water from the torrential streams for irrigation.

Irrigation plays an important role, due to the reduced amount of water availability from rainfalls and the farmers′ inability to “buy” water, because of the economic crisis. Farming and manufacturing activities based on the agricultural activity, as well as other activities of the primary and secondary sector production are a pressing need for a research that will provide adapting systems and information regarding the availability of water and drought conditions. This contributes to the development of the agricultural production for the local population related to agricultural activities or for those who have in mind to occupy with the agricultural sector.

In the current paper, an attempt towards the simulation of the hydrological cycle was performed. All the necessary parameters were created by the ArcGIS 10.2.1 program and afterwards they were given as inputs in the MIKE SHE model. The application aimed to calibrate the MIKE SHE model. Special attention was given regarding the simulation estimation of the runoff process. The ability of the model to reproduce the rainfall conditions and other natural processes prevailing in the study area was tested. The current study is a first-ever attempt to simulate the hydrological basin of Sperchios river using a fully distributed, physical-based, hydrological model.

Research area

General

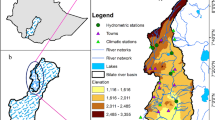
Sperchios River originates from Mount Timfristos (altitude 2.327 m) which occupies a large part of Evritania and Fthiotida regions in central Greece. Having a general direction to the east, the river enters the region of Fthiotida, crosses the homonym valley (Sperchios Valley) between Mount Oiti and the western extension of Mount Othrys before pouring into the Maliakos Gulf. Powered by a host of torrential streams that spring from the mountain Vardousia (2.286 m), Mount Othrys (1.170 m) and Mount Kallidromo (2.116 m), Sperchios Valley is a fertile region with complex vegetation and land use (Paparrizos and Chatziminiadis 2010; Paparrizos 2012; Maris et al. 2014; Paparrizos et al. 2014). Figure 1 represents the Sperchios river basin, including the elevation of the basin.

Fig. 1
figure 1

Study area

Full size image

Topographical and climatological data

The required data were divided into physiographic and climate categories. The topographical data of the area under study were obtained through the digitization of maps 1:50,000 courtesy of the Greek Geographical Army Service. Through maps digitization, the specification of the boundaries of the watershed was achieved.

Geology was analyzed based on maps from the Institute of Geological and Mineral Exploration (IGME 1983).

For vegetation and land cover, the Corine Land Cover database (CLC 2000) was used.

Daily values of meteorological data obtained from eight rainfall stations (Table 1), one meteorological station (Table 2) and three stations with discharge data (Table 3) within the Sperchios river valley were used in the study for the hydrological years 1962–1981. The reason for the selection of these data times series was the fact that the current period was the only period that we had available and common data from all the stations. Before using the data, a homogeneity test was performed (Dingman 1994) to improve the quality of the used data series.

Table 1 Stations with precipitation data
Full size table
Table 2 Station with meteorological data
Full size table
Table 3 Stations with discharge data
Full size table

Methodology

Modeling

As shown in Dingman (2002), a model is a representation of a part of the natural or man-fabricated world, which can initially be categorized as physical, analog or a natural mathematical model (Brooks 1991). In an analog model, observations of a process are used for the simulation of another similar natural process. The mathematical model consists of an explicit, arithmetic, sequential order of equations with logical steps, which converts numerical inputs into numerical outputs (Dingman 2002). Rapid advances in computer technology led to the replacement of natural and analog models by mathematical models.

MIKE SHE model

The modeling system MIKE SHE (Refsgaard and Storm 1995) is based on the model SHE (Système Hydrologique Européen) (Abbott et al. 1986a, b) and has been widely used to examine the hydrological responses in land use changes/land cover, climate and climate variability (Graham and Butts 2005; Zhang et al. 2008), the operation of irrigation (Jayatilaka et al. 1998; Singh et al. 1999), the hydrological manipulations of the flora of wetlands (Thompson et al. 2004), of forest management and forest fires and the impact assessment (Lu 2006; McMichael and Hope 2007) and the sustainable management of groundwater (Demetriou and Punthakey 1999). It contains procedures that can be applied in basic studies including the model structure and internal evaluation model (Butts et al. 2004; Christiansen et al. 2004) as long as model uncertainty analysis (Christiaens and Feyen 2001; Butts et al. 2004; McMichael and Hope 2007). Other areas of study for the MIKE SHE include analyzing the sensitivity and spatial scale effects (Xevi et al. 1997; V′azquez et al. 2002; V′azquez and Feyen 2007), the parameterization of the model calibration and verification (Refsgaard 1997; Andersen et al. 2001; Henriksen et al. 2003; Madsen 2003) and evaluation methods of potential evapotranspiration (PET) (V′azquez and Feyen 2003).

Application—calibration of the MIKE SHE model

Within the physical-based, mathematical MIKE SHE model, the parameters have physical meaning and can theoretically be measured in the field while there is always a range according to the literature in which each parameter takes values. The calibration of the model includes the choice of the parameters that play a key role in the natural process of converting rainfall into runoff each time. The used rainfall-runoff model operates in a daily time step which is sufficient for the purposes of this research which aim towards the management of water resources in the Sperchios River basin, the assessment of the surface runoff from Sperchios basin and consequently the corresponding amount of water to the Maliakos Gulf.

During the calibration of the current hydrological model of this study, emphasis was given towards the successful representation of total water balance, to make possible the successful calibration of all the available observed hydrographs. The main objective of calibration is to reproduce the observed data series of runoff by calculating realistic values for actual evapotranspiration and other water balance parameters. The calibration procedure had as its ultimate objective the correct estimation of surface runoff in Sperchios River basin. A limiting factor in the calibration effort of hydrological model was the unavailability of data for the estuary of Sperchios River basin.

In Sperchios River basin the runoff was simulated in the positions where discharge data were available; these points are in KASTRI, KOMPOTADES and KOMMA (mentioned on Table 3) as shown in Fig. 2. For purposes of calibrating the water balance of Sperchios River basin, available literature data of water balances from the study and management of water resources of Eastern continental Greece were used, provided by the Ministry of Development (2006).

Fig. 2
figure 2

Climatological and discharge stations in Sperchios River basin

Full size image

Statistical indicators—calibration of the model

The following goodness-of-fit statistics were used to determine whether or not there is a successful calibration/validation of the model. These indicators are: (1) the mean absolute error (MAE) (Eq. 1), (2) the relative mean square error (RRMSE) (Eq. 2), (3) the coefficient of efficiency (EF) or otherwise known as the coefficient of Nash–Sutcliffe (Eq. 3), and (4) the coefficient of residual bias (BIAS) (Eq. 4), (Legates and McCabe 1999; Stansoft 2007). The equations of the indicators are as follows:

$${\text{MAE}} = \;\frac{{\sum\limits_{i = 1}^{n} {\left| {O_{i} - P_{i} } \right|} }}{n}$$
(1)
$${\text{RRMSE}} = \;\sqrt {\frac{{\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }}{n}} \frac{1}{{\bar{O}}}$$
(2)
$${\text{EF}} = 1.0 - \frac{{\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )^{2} } }}{{\sum\limits_{i = 1}^{n} {(O_{i} - \bar{O})^{2} } }}$$
(3)
$${\text{BIAS}} = \;\frac{{\sum\limits_{i = 1}^{n} {(O_{i} - P_{i} )} }}{n}$$
(4)

where P i are the values of discharge derived from the model, O i are the values of the observed (historical) discharge and \(\bar{O}\) is the average of the historical discharge.

The MAE and RRMSE take values higher than 0.0 (the optimum value of 0.0), while the EF takes values in the period from −∞ to +∞, while the optimal value is 1.0. The BIAS takes values in the same space with the EF, but the best value is 0.0. Especially for the EF, which is the most important indicator, if it gets a value equal to zero, it means that the model describes the simulated procedures with the same efficiency as the average of observed values, while negative values of the coefficient suggest that the applicability of the model is of the same force as the ′white noise′ (Henriksen et al. 2003).

Water balance

The main hydrological deficit is the actual evapotranspiration, which is a function of potential evapotranspiration and water availability in the root soil layer. Two factors determine the amount of water which evaporates through evapotranspiration. The first factor is the depth of the root system and the second is the ability of soil to capture the crop rooting in soil moisture. The greatest depth is at the root system, the more water ′draws′ the vegetation from the ground, which is evaporated through transpiration. The soil parameters that determine the ability of soil to retain moisture is field capacity and the wilting point. The difference is equal to the amount of water that can be retained by the roots of plants and, therefore, be available for transpiration (DHI 2009).

The basic equation of the water balance is expressed on the basis of the following equation (Eq. 5):

$${\text{PREC}} = {\text{AET}} - {\text{DIR}} - {\text{RF + BIN}} - {\text{BOUT}} \pm \Delta S + \varepsilon$$
(5)

where PREC is the precipitation, AET the actual evapotranspiration, DIR the direct runoff, RF the basic and intermediate runoff, BIN the income from neighboring basins, BOUT the outcome from neighboring basins, ΔS is the change in basin storage at the end of each time step (monthly or yearly)—the positive value of ΔS is the surplus, occurred at the end or each time step, while the negative value is deficit and ε is the total error of the simulation, which is incorporated in the tables with ΔS quantity.

All these quantities are given in the relevant tables and charts in millimeters (mm) of equivalent runoff. To express them in water amount (hm3), they should be multiplied by the area of the basin to which they refer.

Results

MIKE SHE model was calibrated as mentioned in the methodology section and the discharge was simulated. Figures 3, 4, 5 depict the simulated and observed hydrographs in the three discharge stations. For better understanding, daily discharge times were conducted in monthly values. Table 4 presents the simulation results of the statistical indicators which occurred as outputs from the model, while Fig. 6 represents the water balance as occurred from the model, for the available hydrological years in Sperchios River basin. Table 5 presents the simulated coefficients of the annual water balance of Sperchios River basin for the hydrological period 1962–1981. Finally, in Table 6 a comparison of the water balance takes place between the simulated values that occurred from the MIKE SHE model and the observed values provided by the Ministry of Development in a recent research (2006).

Fig. 3
figure 3

Observed and simulated hydrographs at KASTRI position (m3/s)

Full size image
Fig. 4
figure 4

Observed and simulated hydrographs at KOMPOTADES position (m3/s)

Full size image
Fig. 5
figure 5

Observed and simulated hydrographs at KOMMA position (m3/s)

Full size image
Table 4 Calibration results
Full size table
Fig. 6
figure 6

Annual water balance of Sperchios River basin (mm)

Full size image
Table 5 Simulated water balance of Sperchios River basin for the hydrological years 1962–1981
Full size table
Table 6 Comparison of the results of water balance in Sperchios River basin
Full size table

Discussion and conclusions

As shown in the Tables and Figures regarding the simulation of the discharge, the results considered to be satisfactory for KOMPOTADES station, while some minor differentiations appeared during the simulation of the discharge for KASTRI and KOMMA measurement locations. The EF for the simulation period demonstrates the more acceptable values for the simulation period 1962–1981 in KOMPOTADES station were EF = 0.361. This suggests that the model is able to reproduce the runoff mechanisms for different periods which show different hydrological characteristics. Here, it needs to be stated that in periods with high values of discharge (mainly the wither period) the model appeared with several underestimations, comparing to the other periods with decreased runoff which the MIKE SHE model was able to simulate faithfully.

Specifically, from the Figs. 3, 4, 5 it is obvious that the model can successfully simulate the values up to 40–50 m3/s regarding the observed values, while an underestimation appears after these values. Of course, this can be explained by the fact that the model moderates the results and does not take into account some extreme events that can occur in the winter months and constitutes a very possible scenario, especially in the current area that appeared with flooding phenomena (Paparrizos and Chatziminiadis 2010).

Regarding the simulation of the water balance for Sperchios river basin, the results are considered generally very satisfactory and lie within the limits described in such references. Some minor differentiations appear, mainly because in the current research, due to lack of available data, ground hydrology data series as long as incomes from neighboring basins for the model to compute the outputs/inputs and the basin storage in the saturated/unsaturated zone (ΔS).

Similar studies indicated that regarding the simulation of the water balance for Sperchios River basin, the MIKE SHE model was able to simulate very satisfactorily all the hydrological procedures, although in the current research, due to lack of available data the income from neighboring basins was not taken into account. Comparing the results of the current study with the results of the Ministry of Development (2006), the simulated and the observed values showed a strong matching.

In summary, the targets that were set in the current study were to simulate the discharge for the three given points in the main bed of Sperchios River and simulate the water balance of Sperchios River basin through the calibration of the MIKE SHE model to represent all the hydrological processes accurately and reproduce satisfactory results.

Evaluating the results of this study we reached at the following conclusions:

  • To model Sperchios River basin it was necessary to collect and give as inputs a large amount of data because the mathematical model MIKE SHE includes many variables related with all hydrological processes, and especially with the geomorphology of the study area. However, this mathematical model enables the user to simplify or multiply individual hydrological processes, depending on the needs of each application. In the current study, an attempt was performed to use a limited amount of parameters (e.g., choice of modeling subsurface flow with the approach of linear reservoirs) without reducing the accurate representation of the calibration parameters.

  • In the mathematical model MIKE SHE, there are plenty of parameters and options that can be used in the admissions process as input data (e.g., data from GIS). This increases the reliability and flexibility of the model to data management, in comparison with other similar physical-based, distributed models.

  • In mathematical model MIKE SHE, there are a large number of parameters that can potentially be used during calibration. So, for the model to become fully functional and present satisfactory results, it is necessary primarily to correct calibration of the individual parameters of the water balance to reproduce the best possible results that correspond to reality.