Abstract
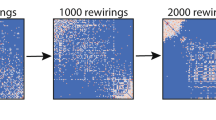
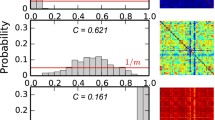
A modular small-world topology in functional and anatomical networks of the cortex is eminently suitable as an information processing architecture. This structure was shown in model studies to arise adaptively; it emerges through rewiring of network connections according to patterns of synchrony in ongoing oscillatory neural activity. However, in order to improve the applicability of such models to the cortex, spatial characteristics of cortical connectivity need to be respected, which were previously neglected. For this purpose we consider networks endowed with a metric by embedding them into a physical space. We provide an adaptive rewiring model with a spatial distance function and a corresponding spatially local rewiring bias. The spatially constrained adaptive rewiring principle is able to steer the evolving network topology to small world status, even more consistently so than without spatial constraints. Locally biased adaptive rewiring results in a spatial layout of the connectivity structure, in which topologically segregated modules correspond to spatially segregated regions, and these regions are linked by long-range connections. The principle of locally biased adaptive rewiring, thus, may explain both the topological connectivity structure and spatial distribution of connections between neuronal units in a large-scale cortical architecture.













Similar content being viewed by others
References
Achacoso TB, Yamamoto WS (eds) (1991) AY’s neuroanatomy of C. elegans for computation. CRC Press, Boca Raton
Atilgan AR, Akan P, Baysal C (2004) Small-world communication of residues and significance for protein dynamics. Biophys J 86(1):85–91
Atmanspacher H, Scheingraber H (2005) Inherent global stabilization of unstable local behaviour in coupled map lattices. Int J Bifurcation Chaos 15:1665–1676
Barabási AL, Albert R, Jeong H (1999) Mean-field theory for scale-free random networks. Phys A Stat Mech Appl 272(1–2):173–187
Blondel VD, Guillaume JL, Lambiotte R, Lefebvre E (2008) Fast unfolding of communities in large networks. J Stat Mech Theory Exp 8(10):1–12
Bollabas B (ed) (1985) Random graphs. Academic Press, London
Breakspear M, Terry JR, Friston KJ (2003) Modulartion of excitatory synaptic coupling facilitates synchronization and complex dynamics in a biophysical model of neuronal dynamics. Network 14:703–732
Bullmore ET, Bassett DS (2011) Brain graphs: graphical models of the human connectome. Annu Rev Clin Psychol 7:113–140
Chan KY, Vitevitch MS (2009) The influence of the phonological neighborhood clustering coefficient on spoken word recognition. J Exp Psychol Hum Percept Perform 35(6):1934–1949
Chan KY, Vitevitch MS (2010) Network structure influences speech production. Cognit Sci 34(4):685–697
Cherniak C (1994) Component placement optimization in the brain. J Neurosci 14(4):2418–2427
Ferrer i Cancho R, Solé RV (2001) The small world of human language. Proc R Soc Lond B 268(1482):2261–2265
Gallos LA, Makse HA, Sigman M (2012) A small world of weak ties provides optimal global integration of self-similar modules in functional brain networks. PNAS 109(8):2825–2830
Gong P, van Leeuwen C (2003) Emergence of scale-free network with chaotic units. Phys A Stat Mech Appl 321(3–4):679–688
Gong P, van Leeuwen C (2004) Evolution to a small-world network with chaotic units. Europhys Lett 67(2):328–333
He Y, Chen ZJ, Evans AC (2007) Small-world anatomical networks in the human brain revealed by cortical thickness from MRI. Oxf J 17(10):2407–2419
Hebb DO (1949) Organization of behaviour: a neuropsychological theory. Wiley, NY
Humphries MD, Gurney K (2008) Network ‘small-world-ness’: a quantitative method for determining canonical network equivalence. PLoS ONE 3(4):e0002051
Innocenti GM, Price DJ (2005) Exuberence in the development of cortical networks. Nat Rev Neurosci 6(12):955–965
Kaneko K (ed) (1993) Theory and applications of coupled map lattices. Wiley, Chichester
Kwok HF, Jurica P, Raffone A, van Leeuwen C (2007) Robust emergence of small-world structure in networks of spiking neurons. Cognit Neurodyn 1(1):39–51
Latora V, Marchiori M (2001) Efficient behavior of small-world networks. Phys Rev Lett 87(19):198701
Laughlin SB, den Ruyter van Steveninck RR, Anderson JC (1998) The metabolic cost of neural information. Nat Neurosci 1(1):36–41
Montoya JM, Solé RV (2002) Small world patterns in food webs. Theor Biol 214(3):405–412
Nakatani H, Khalilov L, Gong P, van Leeuwen C (2003) Nonlinearity in giant depolarizing potentials. Phys Lett A 319(1–2):167–172
Newman MEJ (2004) Fast algorithm for detecting community structure in networks. Phys Rev E 69(6):066133
Newman MEJ (2006) Modularity and community structure in networks. PNAS 103(23):8577–8582
Newman MEJ (ed) (2010) Networks: an introduction. Oxford University Press, Oxford
Rulkov NF (2002) Modeling of spiking-bursting neural behavior using two-dimensional map. Phys Rev E 65:041922
Rubinov M, Sporns O (2010) Complex network measures of brain connectivity: uses and interpretations. NeuroImage 52(3):1059–1069
Rubinov M, Knock SA, Stam CJ (2009a) Small-world properties of nonlinear brain activity in schizophrenia. Hum Brain Mapp 58(2):403–416
Rubinov M, Sporns O, van Leeuwen C, Breakspear M (2009b) Symbiotic relationship between brain structure and dynamics. BMC Neurosci 10:55
Sejnowski TJ, Tesauro G (1989) Building network learning algorithms from hebbian synapses. In: McGaugh JL, Weinberger NM, Lynch G (eds) Brain organization and memory: cells, systems, and circuits. Oxford University Press, New York, pp 338–355
Song S, Miller KD (2000) Competitive Hebbian learning through spike-timing-dependent synaptic plasticity. Nat Neurosci 3(9):919–926
Sporns O (2011) The human connectome: a complex network. Ann N Y Acad Sci 1224(1):109–125
Travers J, Milgram S (1969) An experimental study of the small world problem. Sociometry 32(4):425–443
van den Berg D, Gong P, Breakspear M, van Leeuwen C (2012) Fragmentation: loss of global coherence or breakdown of modularity in functional brain architecture? Frontiers Syst Neurosci 6:20
van den Berg D, v. Leeuwen C (2004) Adaptive rewiring in chaotic networks renders small-world connectivity with consistent clusters. Europhys Lett 65(4):459–464
Vendruscolo M, Dokholyan NV, Paci E, Karplus M (2001) Small-world view of the amino acids that play a key role in protein folding. Phys Rev E 65:061910
Vitevitch MS, Chan KY, Roodenrys S (2012) Complex network structure influences processing in long-term and short-term memory. J Mem Lang 67(1):30–44
Wagner A, Fell DA (2001) The small world inside large metabolic networks. Proc R Soc Lond Ser B Biol Sci 268(1478):1803–1810
Watts DJ, Strogatz SH (1998) Collective dynamics of ‘small-world’ networks. Nature 393(6684):440–442
Zhang LI, Poo MM (2001) Electrical activity and development of neural circuits. Nat Neurosci 4:1207–1214
Acknowledgments
This study was supported by an Odysseus grant from the Flemish Organization for Science, FWO to Cees van Leeuwen.
Author information
Authors and Affiliations
Corresponding author
Appendices
Appendix 1: Evenly distributed points on a sphere
There does not yet exist a solution to evenly distribute points on a sphere for any number of points.
We thus devised the following iterative algorithm to approximate an even distribution of 500 points on the sphere.
-
Step 0: Initialise points at positions drawn randomly from a uniform distribution on the unit sphere, with coordinate vectors \(\mathbf {x}_i\in \mathbb {R}^{3}\), \(i=1,\ldots ,n\), and \(\Vert \mathbf {x}_{i}\Vert =1\).
-
Step 1: Define the crowdedness around a point \(i\) as \(K_{i}=(\sum _{j\ne i} \Vert \mathbf {x}_{i}-\mathbf {x}_{j} \Vert )^{-1}\). Choose the most crowded point \(j\) such that \(K_{j}=\max _{i}{K_{i}}\).
-
Step 2: Given point \(j\), each other point \(k\) moves away from \(j\) in the direction of the vector \(\mathbf {x}_{k}-\mathbf {x}_{j}\), by an amount determined by a linearly dampening function
$$\begin{aligned} F_{jk}=\frac{\alpha }{c}\exp {( -\beta \Vert \mathbf {x}_{j}-\mathbf {x}_{k}\Vert )} \end{aligned}$$where \(\beta =5\) determines how \(F_{jk}\) decreases over distance; large \(\beta\) means repelling force acts over a small spatial distance and vice versa. A systematic trial and error search found \(\beta =5\) to be most successful. The dampening coefficient \(\alpha\) decreases linearly with \(\alpha (t)=1-\frac{t}{T}\) for \(t=0,\ldots ,T-1\). The coefficient \(c=\sqrt{\frac{n}{2}} \max _{k\ne j}{\left( \exp ^{\left( -\beta \Vert \mathbf {x}_{j}-\mathbf {x}_{k}\Vert _{1}\right) }\right) }\) normalises \(F\) so that \(F\in \left( 0,\alpha \sqrt{\frac{2}{n}}\right)\), where \(\frac{2}{\sqrt{n}}\) is the approximate distance between nearest neighbours among an evenly distributed set of points on the sphere.
-
Step 3: Project each point back onto the sphere: \(\frac{\mathbf {x}_{k}-\mathbf {x}_{j}}{\Vert \mathbf {x}_{k}\Vert }\).
-
Step 4: Repeat from Step 1 until \(\frac{n(n-1)}{2}\) iterates have been reached.
For a set of finitely many evenly distributed points on the sphere, the cumulative number of points when moving in the azimuthal angle is a discrete approximation to the surface integral with respect to the azimuthal angle. Thus, we measure the accuracy of the approximated even distribution of points on the sphere as the absolute error between the cumulative number of points (normalised to unity) and the surface integral (normalised to unity). This is calculated for each point. Figure 14 shows the average value of absolute error for all points at the same azimuthal angle as a function of azimuthal angle.
We see in Fig. 14 that the average absolute error is always less than 0.35 %. Since \(n=500\), a 0.4 % error is equal to \(\frac{2}{n}\) and hence corresponds to approximately 2 points more or less than the expected cumulative number of points at any given azimuthal angle given a uniform distribution.
Appendix 2: Network measures
Measures of clustering coefficient, average shortest path length, weighted clustering coefficient, and edge betweenness are taken from (Rubinov and Sporns 2010).
Clustering coefficient
Let \(a_{ij}\) be the entries of the adjacency matrix, i.e. \(a_{ij}=1\) if \(i\) connects to \(j\), and \(a_{ij}=0\) otherwise. The degree of a node with undirected connections is calculated as
The number of triangles pivoting on node \(i\)—pair nodes adjacent to node \(i\) that are themselves connected—is calculated as
Thus the clustering coefficient can be determined as,
Average shortest path length
A path of length \(l\) between nodes \(i\) and \(j\) is a sequence of vertices \(\eta _{i\leftrightarrow j}=(i=i_0,\ldots ,i_l=j)\) with \(a_{i_{k,k+1}}=1\). Let \(l_{ij}\) be the length of the shortest path between \(i\) and \(j\). The average shortest path length is the mean value over all pairwise nodes, calculated as
For disconnected pairs of nodes \(l_{ij}\) is undefined, however, such pairs are excluded in the MATLAB program computation to allow a result.
Modularity
Let \(\Theta =\lbrace \theta _1,\theta _2,\ldots \rbrace\) be a partition of the nodes of the network into modules, i.e. the subsets of nodes that form non-overlapping communities. Let \(\Pi _{\theta _i\theta _j}\) denote the fraction of all edges in the network that connect nodes in module \(\theta _i\) to nodes in module \(\theta _j\). Then the modularity for this set of modules is calculated as
Edge betweenness centrality
Calculated for each edge as the fraction of shortest paths in the network which pass through the edge. Let \(H_{uv}\) be the number of shortest paths that connect nodes \(u\) and \(v\), and let \(H_{uv}(i,j)\) be the number of shortest paths between nodes \(u\) and \(v\) that includes the edge between \(i\) and \(j\).
Then, the edge betweenness value for the edge between \(i\) and \(j\) is calculated as
Small-worldness
Calculated as the normalised ratio of the clustering coefficient to the average shortest path length:
for \(C\) the clustering coefficient and \(L\) average shortest path length of a network, normalised respectively by the corresponding quantities \(C_{\text {rand}}\) and \(L_{\text {rand}}\) for a corresponding random network.
Weighted clustering coefficient
A weighted triangle is determined as the cubic root of the product of the three weighted edges that make a triangle centred on a given node. The sum of all triangles pivoting on a given node \(i\) is
for edge weights \(w_{ij}\), defined by the linear relation
Zero distance corresponds to a weight of 1 and the maximum distance \(\pi\) corresponds to a zero weight. Thus, the weighted clustering coefficient is calculated as
Network wiring cost
The normalised average edge length for all edges of the network is
where \(\pi\) is the maximum edge length that connects two nodes on the shortest arc along the great circle for the network embedded on a unit sphere. A network wiring cost value of 1 indicates an average edge length of \(\pi\), of zero indicates an average edge length of zero, and of \(\frac{1}{2}\) indicates the expected value for randomly distributed edge lengths.
Rights and permissions
About this article
Cite this article
Jarman, N., Trengove, C., Steur, E. et al. Spatially constrained adaptive rewiring in cortical networks creates spatially modular small world architectures. Cogn Neurodyn 8, 479–497 (2014). https://doi.org/10.1007/s11571-014-9288-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11571-014-9288-y