Abstract
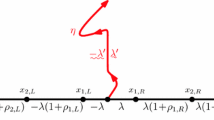
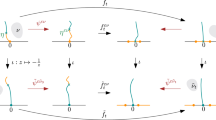
We prove that the chordal contour lines of the discrete Gaussian free field converge to forms of SLE(4). Specifically, there is a constant λ > 0 such that when h is an interpolation of the discrete Gaussian free field on a Jordan domain—with boundary values −λ on one boundary arc and λ on the complementary arc—the zero level line of h joining the endpoints of these arcs converges to SLE(4) as the domain grows larger. If instead the boundary values are −a < 0 on the first arc and b > 0 on the complementary arc, then the convergence is to SLE(4; a/λ - 1, b/λ - 1), a variant of SLE(4).
Similar content being viewed by others
References
Ahlfors, L. V., Conformal Invariants: Topics in Geometric Function Theory. McGraw-Hill Series in Higher Mathematics. McGraw-Hill, New York, 1973.
Beffara, V., The dimension of the SLE curves. Ann. Probab., 36:4 (2008), 1421–1452.
Belavin, A. A., Polyakov, A. M. & Zamolodchikov, A. B., Infinite conformal symmetry in two-dimensional quantum field theory. Nuclear Phys. B, 241 (1984), 333–380.
Bricmont, J., El Mellouki, A. & Fröhlich, J., Random surfaces in statistical mechanics: roughening, rounding, wetting,…. J. Stat. Phys., 42:5–6 (1986), 743–798.
Camia, F. & Newman, C. M., Two-dimensional critical percolation: the full scaling limit. Comm. Math. Phys., 268 (2006), 1–38.
Cardy, J., SLE for theoretical physicists. Ann. Physics, 318 (2005), 81–118.
Coniglio, A., Fractal structure of Ising and Potts clusters: exact results. Phys. Rev. Lett., 62:26 (1989), 3054–3057.
Di Francesco, P., Mathieu, P. & Sénéchal, D., Conformal Field Theory. Graduate Texts in Contemporary Physics. Springer, New York, 1997.
Doyle, P. G. & Snell, J. L., Random Walks and Electric Networks. Carus Mathematical Monographs, 22. Mathematical Association of America, Washington, DC, 1984.
Duplantier, B., Two-dimensional fractal geometry, critical phenomena and conformal invariance. Phys. Rep., 184 (1989), 229–257.
Duplantier, B. & Saleur, H., Exact critical properties of two-dimensional dense self-avoiding walks. Nuclear Phys. B, 290 (1987), 291–326.
— Winding-angle distributions of two-dimensional self-avoiding walks from conformal invariance. Phys. Rev. Lett., 60:23 (1988), 2343–2346.
Foltin, G., An alternative field theory for the Kosterlitz–Thouless transition. J. Phys. A, 34:26 (2001), 5327–5333.
Fröhlich, J. & Spencer, T., The Kosterlitz–Thouless transition in two-dimensional abelian spin systems and the Coulomb gas. Comm. Math. Phys., 81 (1981), 527–602.
Gȩdzki, K., Lectures on conformal field theory, in Quantum Fields and Strings: a Course for Mathematicians, Vol. 1, 2 (Princeton, NJ, 1996/1997), pp. 727–805. Amer. Math. Soc., Providence, RI, 1999.
Giacomin, G., Limit theorems for random interface models of Ginzburg–Landau ∇ϕ type, in Stochastic Partial Differential Equations and Applications (Trento, 2002), Lecture Notes in Pure and Appl. Math., 227, pp. 235–253. Dekker, New York, 2002.
Glimm, J. & Jaffe, A., Quantum Physics. Springer, New York, 1987.
Huber, G. & Kondev, J., Passive-scalar turbulence and the geometry of loops. Bull. Amer. Phys. Soc., DCOMP Meeting 2001, Q2.008.
Isichenko, M. B., Percolation, statistical topography, and transport in random media. Rev. Modern Phys., 64:4 (1992), 961–1043.
Kadanoff, L. P., Lattice Coulomb gas representations of two-dimensional problems. J. Phys. A, 11:7 (1978), 1399–1417.
Kager, W. & Nienhuis, B., A guide to stochastic Löwner evolution and its applications. J. Stat. Phys., 115:5–6 (2004), 1149–1229.
Karatzas, I. & Shreve, S. E., Brownian Motion and Stochastic Calculus. Graduate Texts in Mathematics, 113. Springer, New York, 1988.
Kenyon, R., Dominos and the Gaussian free field. Ann. Probab., 29:3 (2001), 1128–1137.
Kondev, J., Du, S. & Huber, G., Two-dimensional passive-scalar turbulence and the geometry of loops. Bull. Amer. Phys. Soc., March Meeting 2002, U4.003.
Kondev, J. & Henley, C. L., Geometrical exponents of contour loops on random Gaussian surfaces. Phys. Rev. Lett., 74:23 (1995), 4580–4583.
Kondev, J., Henley, C. L. & Salinas, D. G., Nonlinear measures for characterizing rough surface morphologies. Phys. Rev. E, 61 (2000), 104–125.
Kosterlitz, J. M., The d-dimensional Coulomb gas and the roughening transition. J. Phys. C, 10:19 (1977), 3753–3760.
Kosterlitz, J. M. & Thouless, D. J., Ordering, metastability and phase transitions in two-dimensional systems. J. Phys. C, 6:7 (1973), 1181–1203.
Lawler, G. F., Intersections of Random Walks. Probability and its Applications. Birkhäuser, Boston, MA, 1991.
— Strict concavity of the intersection exponent for Brownian motion in two and three dimensions. Math. Phys. Electron. J., 4 (1998), Paper 5, 67 pp.
— An introduction to the stochastic Loewner evolution, in Random Walks and Geometry, pp. 261–293. de Gruyter, Berlin, 2004.
— Conformally Invariant Processes in the Plane. Mathematical Surveys and Monographs, 114. Amer. Math. Soc., Providence, RI, 2005.
Lawler, G. F., Schramm, O. & Werner, W., Values of Brownian intersection exponents. I. Half-plane exponents. Acta Math., 187 (2001), 237–273.
— Values of Brownian intersection exponents. III. Two-sided exponents. Ann. Inst. H. Poincaré Probab. Statist., 38 (2002), 109–123.
— Conformal restriction: the chordal case. J. Amer. Math. Soc., 16 (2003), 917–955.
— Conformal invariance of planar loop-erased random walks and uniform spanning trees. Ann. Probab., 32:1B (2004), 939–995.
Mandelbrot, B., How long is the coast of Britain? Statistical self-similarity and fractional dimension. Science, 156 (1967), 636–638.
Naddaf, A. & Spencer, T., On homogenization and scaling limit of some gradient perturbations of a massless free field. Comm. Math. Phys., 183 (1997), 55–84.
Nienhuis, B., Exact critical point and critical exponents of O(n) models in two dimensions. Phys. Rev. Lett., 49:15 (1982), 1062–1065.
— Critical behavior of two-dimensional spin models and charge asymmetry in the Coulomb gas. J. Stat. Phys., 34:5–6 (1984), 731–761.
den Nijs, M., Extended scaling relations for the magnetic critical exponents of the Potts model. Phys. Rev. B, 27:3 (1983), 1674–1679.
Pommerenke, C., Boundary Behaviour of Conformal Maps. Grundlehren der Mathematischen Wissenschaften, 299. Springer, Berlin–Heidelberg, 1992.
Revuz, D. & Yor, M., Continuous Martingales and Brownian Motion. Grundlehren der Mathematischen Wissenschaften, 293. Springer, Berlin–Heidelberg, 1999.
Rohde, S. & Schramm, O., Basic properties of SLE. Ann. of Math., 161 (2005), 883–924.
Saleur, H. & Duplantier, B., Exact determination of the percolation hull exponent in two dimensions. Phys. Rev. Lett., 58:22 (1987), 2325–2328.
Schramm, O., Scaling limits of loop-erased random walks and uniform spanning trees. Israel J. Math., 118 (2000), 221–288.
Schramm, O. & Sheffield, S., Harmonic explorer and its convergence to SLE4. Ann. Probab., 33:6 (2005), 2127–2148.
Sheffield, S., Gaussian free fields for mathematicians. Probab. Theory Related Fields, 139 (2007), 521–541.
Smirnov, S., Critical percolation in the plane: conformal invariance, Cardy’s formula, scaling limits. C. R. Acad. Sci. Paris Sér. I Math., 333 (2001), 239–244.
Spencer, T., Scaling, the free field and statistical mechanics, in The Legacy of Norbert Wiener: A Centennial Symposium (Cambridge, MA, 1994), Proc. Sympos. Pure Math., 60, pp. 373–389. Amer. Math. Soc., Providence, RI, 1997.
Werner, W., Random planar curves and Schramm–Loewner evolutions, in Lectures on Probability Theory and Statistics, Lecture Notes in Math., 1840, pp. 107–195. Springer, Berlin–Heidelberg, 2004.
Author information
Authors and Affiliations
Corresponding author
Additional information
During the revision process of this article, Oded Schramm unexpectedly died. I am deeply indebted for all I learned working with him, for his profound personal warmth, for his legendary vision and skill. There was never a better colleague, never a better friend. He will be dearly missed. (Scott Sheffield)
Rights and permissions
About this article
Cite this article
Schramm, O., Sheffield, S. Contour lines of the two-dimensional discrete Gaussian free field. Acta Math 202, 21–137 (2009). https://doi.org/10.1007/s11511-009-0034-y
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11511-009-0034-y