Abstract
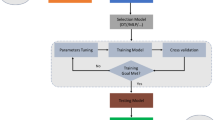
Sensitivity analysis of hydrological model is the key for model uncertainty quantification. However, how to effectively validate model and identify the dominant parameters for distributed hydrological models is a bottle-neck to achieve parameters optimization. For this reason, a new approach was proposed in this paper, in which the support vector machine was used to construct the response surface at first. Then it integrates the SVM-based response surface with the Sobol’ method, i.e. the RSMSobol’ method, to quantify the parameter sensitivities. In this work, the distributed time-variant gain model (DTVGM) was applied to the Huaihe River Basin, which was used as a case to verify its validity and feasibility. We selected three objective functions (i.e. water balance coefficient WB, Nash-Sutcliffe efficiency coefficient NS, and correlation coefficient RC) to assess the model performance as the output responses for sensitivity analysis. The results show that the parameters g1 and g2 are most important for all the objective functions, and they are almost the same to that of the classical approach. Furthermore, the RSMSobol method can not only achieve the quantification of the sensitivity, and also reduce the computational cost, with good accuracy compared to the classical approach. And this approach will be effective and reliable in the global sensitivity analysis for a complex modelling system.
Similar content being viewed by others
References
Andres T H, 1997. Sampling methods and sensitivity analysis for large parameter sets. Journal of Statistical Computation and Simulation, 57(1–4): 77–110.
Ascough II J C, Green T R, Ma L et al., 2005. Key criteria and selection of sensitivity analysis methods applied to natural resource models. In: International Congress on Modeling and Simulation Proceedings. Salt Lake City, UT, November 6–11, 2005: 2463–2469.
Bahremand A, De Smedt F, 2008. Distributed hydrological and sensitivity analysis in Torysa watershed, Slovakia. Water Resources Management, 22: 393–408.
Brockmann D, Morgenroth E, 2007. Comparing global sensitivity analysis for a biofilm model for two-step nitrification using the qualitative screening method of Morris or the quantitative variance-based Fourier Amplitude Sensitivity Test (FAST). Water Science & Technology, 56(8): 85–93.
Campolongo F, Cariboni J, Saltelli A, 2007. An effective screening design for sensitivity analysis of large models. Environmental Modelling and Software, 22: 1509–1518.
Cui Q A, He Z, Che J G, 2006. SVM-based nonparametric dual response surface methodology. Journal of Tianjin University, 39(8): 1008–1014. (in Chinese)
Engeland K, Xu C Y, Gottschalk L, 2005. Assessing uncertainties in a conceptual water balance model using Bayesian methodology. Hydrological Sciences Journal, 50(1): 45–63.
Fieberg J, Jenkins K J, 2005. Assessing uncertainty in ecological systems using global sensitivity analyses: A case example of simulated wolf reintroduction effects on elk. Ecological Modeling, 187: 259–280.
Frey H C, Patil S R, 2002. Identification and review of sensitivity analysis methods. Risk Analysis, 22(3): 553–578.
Fu Xiang, Chu Xuefeng, Tan Guangming, 2010. Sensitivity analysis for an infiltration-runoff model with parameter uncertainty. Journal of Hydrologic Engineering, 15(9): 243–251.
Ginot V, Gaba S, Beaudouin R et al., 2006. Combined use of local and ANOVA-based global sensitivity analyses for the investigation of a stochastic dynamic model: Application to the case study of an individual-based model of a fish population. Ecological Modeling, 193: 479–491.
Hamby D M, 1994. A review of techniques for parameter sensitivity analysis of environmental models. Environmental Monitoring and Assessment, 32(2): 135–154.
He Z, Cui Q A, 2006. A study on the small sample response surface methodology based on SVM. Industrial Engineering Journal, 9(5): 6–10, 27. (in Chinese)
Helton J C, Johnson J D, Sallaberry C J et al., 2006. Survey of sampling-based methods for uncertainty and sensitivity analysis. Reliability Engineering and System Safety, 91: 1175–1209.
Jakeman A J, Letcher R A, Norton J P, 2006. Ten iterative steps in development and evaluation of environmental models. Environmental Modelling & Software, 21(5): 602–614.
Lenhart T, Eckhardt K, Fohrer N et al., 2002. Comparison of two different approaches of sensitivity analysis. Physics and Chemistry of the Earth, 27: 645–654.
Liu Y, Sun F, 2010. Sensitivity analysis and automatic calibration of a rainfall-runoff model using multi-objectives. Ecological Informatics, 5: 304–310.
McKay M D, 1995. Evaluating prediction uncertainty. Los Alamos National Laboratory Technical Report NUREG/CR-6311, LA-12915-MS.
Myers R H, Montgomery D C, Vining G G et al., 2004. Response surface methodology: A retrospective and literature review. Journal of Quality Technology, 36(1): 53–77.
Pappenberger F, Beven K J, Ratto M et al., 2008. Multi-method global sensitivity of flood inundation models. Advances in Water Resources, 31: 1–14.
Plischke E, 2010. An effective algorithm for computing global sensitivity indices (EASI). Reliability Engineering and System Safety, 95: 354–360.
Ratto M, Pagano A, Young P, 2007. State dependent parameter metamodelling and sensitivity analysis. Computer Physics Communications, 177: 863–876.
Ren Q W, Chen Y B, Shu X J, 2010a. Global sensitivity analysis of Xinanjiang model parameter based on Extend FAST method. Acta Scientiarum Naturalium Universitatis Sunyatseni, 49(3): 127–134. (in Chinese)
Ren Q W, Chen Y B, Zhou H L et al., 2010b. Global sensitivity analysis of TOPMODEL parameters based on Sobol method. Yangtze River, 41(19): 91–94, 107. (in Chinese)
Saltelli A, Tarantola S, Campolongo F et al., 2004. Sensitivity Analysis in Practice: A Guide to Assessing Scientific Models. John Wiley & Sons, Ltd.
Sathyanarayanamurthy H, Chinnam R B, 2009. Metamodels for variable importance decomposition with applications to probabilistic engineering design. Computers & Industrial Engineering, 57: 996–1007.
Sobol’ I, 1993. Sensitivity analysis for non-linear mathematical models. Mathematical Modeling & Computational Experiment (English Translation), 1: 407–414.
Song X M, Kong F Z, 2010. Application of Xinanjiang model coupling with artificial neural networks. Bulletin of Soil and Water Conservation, 30(6): 135–138, 144. (in Chinese)
Song X M, Zhan C S, Kong F Z et al., 2011a. A review on uncertainty analysis of large-scale hydrological cycle modeling system. Acta Geographica Sinica, 66(3): 396–406. (in Chinese)
Song X M, Zhan C S, Kong F Z et al., 2011b. Advances in the study of uncertainty quantification of large-scale hydrological modeling system. Journal of Geographical Sciences, 21(5): 801–819.
Stephens D W, Gorissen D, Crombecq K et al., 2011. Surrogate based sensitivity analysis of process equipment. Applied Mathematical Modelling, 35: 1676–1687.
Tang Y, Reed P, van Werkhoven K et al., 2007 Advancing the identification and evaluation of distributed rainfall-runoff models using global sensitivity analysis. Water Resources Research, 43(6): W06415.
Tong C, 2010. Self-validated variance-based methods for sensitivity analysis of model outputs. Reliability Engineering and System Safety, 95(3): 301–309.
van Griensven A, Meixner T, Grunwald S et al., 2006. A global sensitivity analysis tool for the parameters of multi-variable catchment model. Journal of Hydrology, 324(1–4): 10–23.
Wang G S, Xia J, Chen J F, 2010. A multi-parameter sensitivity and uncertainty analysis method to evaluate relative importance of parameters and model performance. Geographical Research, 29(2): 263–270. (in Chinese)
Warmink J J, Janssen J A E B, Booij M J et al., 2010. Identification and classification of uncertainties in the application of environmental models. Environmental Modelling & Software, 25(12): 1518–1527.
Xia J, Wang G S, Lv A F et al., 2003. A research on distributed time variant gain modeling. Acta Geographica Sinica, 58(5): 789–796. (in Chinese)
Xia J, Wang G S, Tan G et al., 2005. Development of distributed time-variant gain model for nonlinear hydrological systems. Science in China (Series D), 48(6): 713–723.
Xia J, Ye A Z, Qiao Y F et al., 2007. An application research on distributed time-variant gain hydrological model in Wuding River of Yellow River. Journal of Basic Science and Engineering, 2007, 15(4): 457–465. (in Chinese)
Xu C, Gertner G, 2007. Extending a global sensitivity analysis technique to models with correlated parameters. Computational Statistics & Data Analysis, 51(12): 5579–5590.
Author information
Authors and Affiliations
Corresponding author
Additional information
Foundation: National Key Basic Research Program of China, No.2010CB428403; National Grand Science and Technology Special Project of Water Pollution Control and Improvement, No. 2009ZX07210-006
Author: Song Xiaomeng (1987–), Master Candidate, specialized in hydrology.
Rights and permissions
About this article
Cite this article
Song, X., Zhan, C., Xia, J. et al. An efficient global sensitivity analysis approach for distributed hydrological model. J. Geogr. Sci. 22, 209–222 (2012). https://doi.org/10.1007/s11442-012-0922-5
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11442-012-0922-5