Introduction

Recently designed flapping micro air vehicles have been developed inspired by insect flight [1–3]. These flapping MAVs generate both lift and thrust by flapping their sail-like wing structures that deform primarily due to aerodynamic loading [3], Fig. 1. Whereas flapping MAVs typically employ slack wings, the wings of most insects are very stiff compared to the sail-like wing structures of MAV wings (e.g. [4]). How insect wings function structurally under dynamic wing loading is not yet fully understood, although existing studies have generated novel insight in how the venation pattern of insects is critical for their load baring capacity and aeroelastic function. Counter-intuitively the corrugated wings of insects provide good aerodynamic performance at low Reynolds numbers [5–9], while providing good structural strength and stiffness [6]. Numerical analyses of insect wings have been performed by Smith [10], Kesel et al. [11], Herbert et al. [12], Combes and Daniel [13–15] and Wootton et al. [16] to better understand the structural function of insect wings under different loading regimes. Smith [10] performed a modal analysis of a quasi-two-dimensional finite element model (FEM) of the fore- and hindwing of a moth, to correlate the distribution of mass and stiffness. Kesel et al. [11] increased model fidelity to study structural stabilization of dragonfly wings by vein corrugation. Herbert et al. [12] numerically explored the mechanisms that lead to the umbrella effect, a mechanism of camber generation in the hindwing fans of orthopteroid and dictyopteroid insects, as described by Wootton [17]. They built cambered FEMs of the hindwing of a grasshopper (Schistocerca gregaria). Combes and Daniel [15] created a quasi- two-dimensional FEM to explore how damping affects a Manduca sexta forewing. Wootton et al. [16] performed a modal and impact analysis on a slightly cambered simplified model of a Manduca sexta wing. Their results indicate that the natural vibration frequency of a Manduca wing is equal to the flapping frequency of Manduca in flight. They also addressed several challenges previous studies encountered in accurately describing wing morphology.

Here we focus on the three-dimensional structural function of dragonfly wings (Fig. 2), because their venation pattern has remained surprisingly similar during their evolution, suggesting this conserved feature plays an important role in flight. The Protodonata, the ancestors of the dragonflies (Odonata), were among the earliest fliers in the Carboniferous.

Fig. 1
figure 1

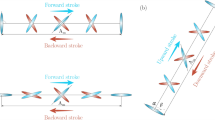
DelFly, a flapping wing micro aerial vehicle inspired by insect flight with slack sail-like wings [3]

Full size image
Fig. 2
figure 2

Photograph (a) of a dragonfly Sympetrum vulgatum forewing with inset images (b t/m g) of the wings detailed structure captured by scanning electron microscopy (positions are approximated). Leading and trailing edge protuberances are believed to produce an increase in lift [43]. (b) Protuberances on leading edge. (c) The nodus of the wing. (d) The wing tip. (e) Vein crossing near the wing root. (f) Trailing edge with protuberances. (g) Wing surface near the wing tip

Full size image

Approximately 350 million year old fossils of Meganeuridae tell us that they flew with wingspans of up to 75 cm. Their wings are similar enough to modern shapes to suggest comparable flight capabilities, although perhaps with less refinement [18, 19]. Modern dragonfly wings have similar wing architecture, but are much smaller in size. The relatively constant wing architecture across dragonfly evolution suggests that the wing architecture of dragonflies functions well over a large range of wingspans. Furthermore, dragonflies are among the more agile flyers. They hunt in flight, are highly manoeuvrable and even mate mid-air. Dragonflies often cope with accelerations of up to 4 g in a straight line and 9 g in steep turns as documented in high speed video recordings [20]. This shows that dragonfly wings most likely have evolved into effective wings that function well under diverse high-performance flight conditions. Understanding how these wings function structurally could, therefore, inspire the design of more effective wings for insect-sized micro air vehicles.

In our structural analysis of dragonfly wings we digitized a dragonfly fore- and hindwing. The geometry of the forewing was captured accurately enough to be modeled well with an array of linked beams and shells to obtain an efficient Finite Element Model. We use this FEM to reveal deformations, and natural vibration characteristics of a dragonfly forewing, to obtain better insight in the functional morphology of dragonfly wings.

Materials and Methods

We chose to study dragonfly (Sympetrum vulgatum) wings. The fore- and hindwing were digitized using the micro computed tomography (micro-CT) scanning method. The forewing geometry is subsequently converted into a FEM for the Abaqus (6.5-1, Dassault Systèmes) solver. For structural analysis of the wing we gathered wing cuticle properties and wing kinematics from literature. Thereupon we made a simplified analytical model of the aerodynamic and inertial wing loads during hovering flight. Combined, we obtain a three-dimensional structure and load model of a dragonfly wing.

Insect Collection and Treatment

We caught a dragonfly (Sympetrum vulgatum) near a pond in the mid-eastern part of The Netherlands. To preserve the dragonfly we stored it in a one to one solution of water and alcohol, directly after we gassed the dragonfly with ethyl-acetate.

Micro CT Scan of Dragonfly Wing

After exploring several digitizing methods such as stereo photography, 3D laser scanning [21] and wing sectioning techniques we selected the micro computed tomography (micro-CT) technique. A micro-CT scanner creates a 3D stack of cross-sections throughout the wing based on X-ray imaging. SkyScan at Anvers (Belgium) kindly sponsored two days of scanning time on their high-resolution SkyScan 1172 micro-CT scanner. This proved to be enough time for scanning one (n = 1) fore- (single wing span 28,8 mm) and hindwing (single wing span 26,8 mm) after several initial trials. Before scanning, we dried the wing for twelve hours at room temperature. Drying deforms the wing but is necessary to reduce noise and scatter. Both fore- and hindwing of Sympetrum vulgatum were scanned with a resolution of 7.2 μm. This means that every pixel in each of the resulting cross-sectional images has a dimension of 7.2 × 7.2 μm. Also the distance between two successive images in the stack is 7.2 μm. The scans resulted in a total of 3,997 cross-sectional images for the forewing and 3,718 images for the hindwing. The scan provides us with three dimensional information of the dragonfly wing, including vein corrugation and thickness distribution. We wrote a dedicated Matlab program (Matlab 7.0; The Mathworks) to digitally smooth the cross-sections and subsequently reconstruct the wings (Figs. 3 and 4). The gray-values in Figs. 3 and 4 represent wing thickness. Dark indicates thick areas whereas light areas are thin. Although we used a state of the art micro-CT scanner, dragonfly wings still proved to be challenging thin. Especially for the hindwing in Fig. 4; 56% of its membrane area has a thickness less than the resolution of the scan. Fortunately, roughly 96% of the area of the forewing proved thick enough for a three-dimensional scan. We therefore focus our study on the forewing and assume that the area with a thickness smaller than the scan resolution (approximately 4%) has a thickness of 3.6 μm; half the scan resolution.

Fig. 3
figure 3

(a) Digital reconstruction of the forewing of Sympetrum vulgatum. Dark areas are thick, light areas are thin (linear scale from dark to light). (b–e) Cross-sectional micro-CT image near the wing root showing the highly corrugated wing architecture build up by the wings veins and membrane. Cross sections more distant of the root (c–e) show less corrugation and the cross section near the wing tip (e) reveils the hollow pterostigma

Full size image
Fig. 4
figure 4

(a) Digital reconstruction of the hindwing of Sympetrum vulgatum. Dark areas are thick, light areas are thin (linear scale from dark to light). (b–e) Cross-sectional micro-CT image near the wing root showing the highly corrugated wing architecture build up by the wings veins and membrane. Cross sections more distant of the root (c–e) show less corrugation and the cross section near the wing tip (e) reveils the hollow pterostigma. The main difference between this figure and 3 are the much thinner veins and membrane

Full size image

The Finite Element Model

We wrote dedicated Matlab software to convert the digitized three-dimensional geometry into a suitable finite element model to analyze the mechanical function of the wing under representative loading conditions. Finite element models can be made out of volumetric elements or structural elements stretched between nodes. We chose to use structural elements because this results in effective data handling and an easy adaptable model structure. Beam elements (Abaqus: B31 elements) are used to represent wing veins, the membranes between the veins were represented by thin-shell elements having small strain (Abaqus: STRI3 elements). The elements are stretched between nodes assigned at the positions of crossing veins. Based on the micro-CT scan, nodes and elements were automatically assigned by custom 3D Matlab scripts. In total, the forewing was modeled with the use of 543 nodes, 823 beams and 998 shell elements. We could not further refine the FEM model due to the complexity involved to program this without sacrificing the geometric accuracy. To check if the number of elements in our FEM model was appropriate for numerical convergence we performed a literature survey. Combes and Daniel [13–15] found an asymptotic solution for their FEM model of a Manduca sexta wing for 865 elements and up (FEM solver MSC Marc/Mentat 2001). Considering the similarity in wing dimensions and number of elements and the quality of the solution we obtained, we are confident we performed an accurate FEM analysis.

The thickness of each element was determined based on the micro-CT image stack by a custom Matlab script. The beam element thicknesses are averages of the thicknesses around the nodes of the beams (in a 10 × 10 pixel area). The cross-sections of the beams were defined as hollow pipes with a wall thickness of ¾th of the beam radius. We measured this as an average in ten cross-sectional micro-CT images evenly distributed over the wing length. To calculate the average thickness of each membrane we took 10% of each membrane area at its centre. The thickness distribution is manually checked for anomalies. We then adapted values of 17 beam elements and 4 shell elements to the average of surrounding thickness values to correct identified anomalies. The resulting model provides us with an accurate shell and beam thickness distribution of the wing. The wing model is fixed by restricting all degrees of freedom of four nodes at the root. The micro-CT scan shows much scatter around this area because of remaining insect body parts. We therefore manually model the wing root approximating the root shown in Fig. 2. Loads are modeled as pressure loads using a quasi steady model, neglecting unsteady aerodynamic effects. The aerodynamic load acting on each shell element is modeled as a uniform pressure load calculated using an analytic pressure distribution model. Inertial loads were modeled as line pressure loads on beams and uniform pressure loads on shell elements. To perform the FEM analysis we developed custom Matlab software that generates an input file for the Abaqus solver. This text file contains information regarding the geometry, material properties, loads and type of analysis. Abaqus statically analyzed the wing deformations and stresses. Also free vibration analyses were performed to extract the wing’s natural vibration modes. The latter is done by a perturbation step in which the natural vibration frequency is calculated using the Lanczos method [22]. We performed an analysis of the natural vibration modes of a two- and three-dimensional geometrical wing model (in the 2-D model we made the z-coordinate identical for all nodes; note that doing this the vein and membrane models remained 3D). Comparing the results of non-linear and linear simulations gave similar results, because the deformations are relatively small (less than 5.5% of wing length). Therefore we decided to perform linear analysis, neglect nonlinear geometric effects, to reduce computational time.

Dragonfly Wing Material Properties

For the Finite Element Analysis we needed the material properties of our dragonfly (Sympetrum vulgatum) wing. Therefore we collected averaged data from literature. The material density of wing cuticle ρc is taken as 1,200 kg/m3 (measured in biological materials by Wainwright et al. [23], and confirmed by Vincent and Wegst [24]) and we used a Poisson’s ratio ν of 0.49 [23]. Combes and Daniel [13–15] also used a Poisson’s ratio of 0.49 and tested the effects of using a Poisson’s ratio of 0.3 and found the effect to be negligible. In our analysis we took the material stiffness of the wing (Young’s modulus, E) constant throughout the wing for both the veins and membranes, similar to Smith [10] and Kesel et al. [11]. We further took an average vein stiffness of 6 GPa [12], and for the membrane stiffness we took a value of 3.75 GPa [24]. Some studies revealed that the Young’s modulus can vary widely within a wing [25] and that some proteins, such as resilin, can alter local properties [26, 27]. However, measuring spatial material property variations accurately in concert with the 3D wing structure is still out of scope of present technology.

To calculate wing loads during hovering flight, insect properties like body mass, wing mass and wing kinematics are needed. Because we immediately preserved our sample from drying we used the average Sympetrum vulgatum body mass as 225 mg as measured for three samples by Rüppell [28]. The wing mass was calculated by multiplying the wing volume, as measured in the micro-CT image stack, by the cuticle density. The total wing mass appeared to be 3.4 mg, which is 1.5% of its body mass. This value is in the usual range of wing to body mass ratios; usually between 0.5–5% of body mass; measured by Ellington [29]. The mass of haemolymph in the hollow veins was taken into account. We took equal density for cuticle and haemolymph and assume this error to be negligible. Possible flow of heamolymph within the veins is also neglected.

Dragonfly Wing Kinematics

In one flap cycle, the wing revolves around the hinge back and forth at roughly constant angle of attack, while rotating along the spanwise axis during stroke reversal at the beginning and end of a stroke; pronation and supination. When rotating from down- to upstroke, the morphological underside of the wing rotates to face upwards and this is called supination. From up- to downstroke the morphological underside of the wing rotates to face downwards again and this is called pronation. We modeled the flapcycle as a sinusoidal motion:

$$ \varphi {\left( t \right)} = \Phi \cdot \sin {\left( {\omega _{{flap}} t} \right)} $$

Here \( \varphi (t) \) is the stroke angle of the wing, which depends on time t. The flapping frequency \( {f_{flap}} \) is taken as 32.3 Hz, which yields angular frequency \( {\omega_{flap}} = 2\pi f = \) 203 rad/s, measured by Rüppell [28]. The flapping amplitude Φ is taken to be 60°, which is a representative average value for Odonata flapping amplitudes [28, 30]. A full stroke covers twice the (mathematical) wing stroke amplitude; from peak-to-peak the wing revolves over an angle of 120°. Usually, the wing follows a figure eight-like path during the stroke cycle. This occurs in a plane with an inclination angle (β) with the horizontal [30]. For simplicity we assume that the wings flap in a horizontal stroke plane during hovering insect flight as described by Ellington [18] (Fig. 5). The angle of attack of the wing during flapping is assumed to be 30° on average for both the up- and downstroke (Fig. 5), which we estimated based on values found for several insects in literature [31, 32, 38].

Fig. 5
figure 5

Side view insect body. (a) Stroke plane is assumed to the horizontal. (b) Angle of attack is assumed to be 30°

Full size image

Dragonfly Forewing Loading

During flapping, the wing experiences both inertial and aerodynamic loads that need to be carried by the wing structure. Previous studies [13, 15, 29, 33, 34] suggested that the inertial loads are higher than the aerodynamic loads, from 2 [31] up to 10 times [34]. If such a load ratio also holds for dragonfly wings is unknown. To calculate the wing loads we made an analytical model of both the aerodynamic load needed to support the weight of the animal, and the inertial loads that result from the flapping motion of the wing that can support the weight.

Aerodynamic load model

We focused on the lift forces the wing needs to bear to oppose body weight, in this force calculation we neglected the loading of the wing due to drag force. Lift in flapping flight is generated by three distinct mechanisms: delayed stall, rotational circulation and wake capture. Delayed stall generates a leading edge vortex (LEV) during the swing phases of the stroke [35–38]. Rotational circulation and wake capture occur primarily during stroke reversal, while the LEV is prominent mid stroke. Because the total lift generated during the swing phase of the wing is typically considerably higher than the lift generated during stroke reversal [38], we focused on lift generated by delayed stall; the LEV. Another aerodynamic load component is known as ‘added mass’ or ‘virtual mass’ [39]. The added mass varies from 0.3 up to 1.2 times the wing mass [33, 40, 41]. Added mass is difficult to model accurately and smaller than lift force, therefore we neglect it in our basic force model. Finally we ignore drag force altogether, because an accurate estimate of both its magnitude and distribution over the wing is still unavailable for dragonflies.

We assumed that average lift generated by a forewing during a flapcycle is equal to ¼ of the weight W of the insect (because of its four wings) and equal during down- and upstroke:

$$ \overline L = \frac{1}{4} \cdot W $$

The aerodynamic load model was based on blade element theory [40, 42]:

$$ \overline L = \frac{{{\rho_{air}}}}{{2T}}\mathop \smallint \limits_0^T \mathop \smallint \limits_0^r \mathop \smallint \limits_0^c {\left( {\dot{\varphi }(t) \cdot x} \right)^2} \cdot {C_l}(x)dydx\,dt $$

Here, T (=1/f) is the period of one flapcycle, ρair the air density at sea level (1.225 kg/m3), x the spanwise distance from the root, r the wing length, y the position on the chord c, and t is time. We scale the lift from a unit elliptical lift distribution, with maximal lift at the base and zero lift at the wing tip, which is typical for fixed wing aircraft, but most likely a substantial simplification for insect wings. The angular velocity of the wing is:

$$ \dot{\varphi }(t) = - {\omega _{{flap}}} \cdot \Phi \cdot \cos ({\omega _{{flap}}}t) $$

To distribute the lift over the wing we first distributed the lift spanwise over wing chord sections with width dx using the chord, speed and lift coefficient distribution. Next we distributed the spanwise lift distribution C l (x) chordwise using the following model for the chordwise pressure distribution:

$$ {C_l}(x) = \mathop \smallint \limits_0^c {C_p}\left( {x,y} \right)dy $$

The chordwise pressure coefficient distribution over the wing C p(x,y) is modeled based on two second-order polynomials. The first polynomial \( \left( {{P_1}(y) = \alpha 0 + \alpha 1 \cdot y + \alpha 2 \cdot {y^2}} \right) \) is defined from the leading edge (y LE  = 0) to the aerodynamic centre (y ac ) and the second polynomial \( \left( {{P_2}(y) = b0 + b1 \cdot y + b2 \cdot {y^2}} \right) \) from y ac to the trailing edge (y TE  = C). The peak of the polynomial distribution is assumed to be at y ac (at 1/4th of the chord length from the leading edge). The pressure difference distribution can now be calculated via:

$$ \Delta P\left( {x,y} \right) = \frac{{{\rho_{air}}}}{2}{\left( {\omega (t) \cdot x} \right)^2} \cdot {C_p}\left( {x,y} \right) $$

In this way we obtain a double curved pressure distribution over the wing area, which depends on the local pressure coefficient, angular velocity, spanwise position and time. For our FEM analysis we determined the average pressure load for all individual shells. In this we assumed that the pressure distribution over the shell is uniform.

Inertial load model

Inertial loads are caused by accelerating wing mass, we considered accelerations due to stroke and neglected accelerations due to angle of attack changes. The inertial loads due to stroke are calculated according to:

$$ F\left( {x,t} \right) = \ddot{\varphi }(t) \cdot x \cdot \left( {\frac{{dm}}{{dx}}} \right)dx $$

Here the angular acceleration is modeled based on a sinusoidal stroke:

$$ \ddot{\varphi }(t) = - {\omega _{{flap}}}^{2} \cdot \Phi \cdot \sin ({\omega _{{flap}}}t) $$

For our FEM the local masses are calculated for each element: We multiplied the volumes of each beam and shell element with the cuticle density ρ c . The accelerations due to wing stroke were calculated at the centre of each element. We took the mass of haemolymph in hollow veins into account, thereby taking haemolymph density equal to cuticle density. We divided the inertial force by element area to obtain inertial ‘pressure loads’ on each element.

Load cases

We analyzed four load cases that occur during the upstroke and four that occur during during downstroke of the wing (Fig. 6). The difference between the four upstroke and downstroke load cases is the orientation of the airfoil with respect to the loading; this is significant, because an insect airfoil is asymmetric. The loadcases were defined as follows; (i) Maximum aerodynamic lift loading, which occurs at midstroke φ = 0°, in our model, this lift points upwards opposing gravity during the upstroke and downstroke. (ii) Maximum load due to inertia occurs in the horizontal plane at stroke reversal (at φ = ±60°) during supination and pronation. (iii) At φ = ±30° four combined aerodynamic and inertial load cases were studied during both acceleration and deceleration of the wing for the upstroke and downstroke case. The resulting load directions depend on the combination of the aerodynamic and inertial load, while the orientation of the airfoil depends on the flapping phase; downstroke vs. upstroke.

Fig. 6
figure 6

Eight load cases during hovering flight. Inertial loads are in the horizontal direction and reverse during stroke reversal (pronation and supination). During stroke reversal the inertial loads act perpendicularly to the wing surface. The lift and inertial loads build up the resultant load vector. The indicated angles represent stroke positions

Full size image

Results and Discussion

Micro computed tomography scanning proved to be a successful method to digitise a dragonfly forewing in three dimensions. Subsequently created thickness distributions showed decreasing thickness of veins and membranes from root to tip and from leading to trailing edge. We analysed results from the numerical analysis using custom Matlab algorithms. Maximum inertial loads appeared higher than maximum aerodynamic loads in spanwise direction. Structural deformations were small, the maximum deflections were found during stroke reversal (1.5 mm) and were located at the wing tip. The numerical analyses also revealed that wing bending during upstroke was higher when compared to downstroke. The latter is likely caused by the asymmetrical shape of the wing due to camber and positions of the valleys and hills in the wing build up by radial veins [17]. Our vibration analysis shows that the wing’s first natural frequency in vacuum is approximately 4.8 times higher than the flapping frequency of Sympetrum vulgatum.

Digitisation and Image Analysis of a Dragonfly Wing

Our results show that three-dimensional digitisation of thick insect wings, such as those from dragonflies, is possible when using modern micro-CT scanners. Micro-CT proved to be a relatively easy, fast and efficient way to capture the morphology of a dragonfly wing (Figs. 3, 4). The only downside of micro CT-scanning is that our wings were slightly deformed near the trailing edge, because the wings needed to be dried to reduce scatter due to evaporation in the warm scanner. The deformations due to drying most likely affected wing stiffness to some degree. The trailing edge veins and membrane are, however, significantly thinner than the rest of the wing, which decreases the effect of local deformation on wing stiffness, because it balances their relative large distance with respect to the centroid of the wing. We determined the thickness distribution of the wing (Fig. 7) based on the cross-sectional image stack of the wing. As expected, thick veins are located near the wing root and the leading edge. Some of the continuous veins that span from leading to trailing edge are thicker as well. The thicknesses of thick veins range from 75 to 150 μm. The veins that form the hexagonal pattern are thinner, with thickness ranging from 10 to 50 μm. The thickness distribution of membranes is similar; thick membranes near the leading edge and root, ranging between 15 and 25 μm. Thin membranes range in thickness from 3.6 μm up to 15 μm. The hollow pterostigma of the wing has a maximum thickness, measured from the bottom to top side of the pterostigma, of approximately 220 μm.

Fig. 7
figure 7

Thickness distribution of the forewing of Sympetrum vulgatum. (a) Thickness distribution of the veins. (b) Thickness distribution of the membranes

Full size image

Load Distributions

We compared the maximum aerodynamic load at midstroke with the maximum inertial load at stroke reversal. The loads are summed along the chord to obtain a spanwise distribution along the wing (Fig. 8). The distributions are similarly shaped from root to tip, with local maxima for inertial load at the nodus (±45% wing length r) and pterostigma (±85% r). The maximum aerodynamic load is found at about 65% of the wingspan (r). We found that the inertial forces along the wingspan are approximately 1.5–3 times higher than the aerodynamic forces. This matches the estimation of Ennos [31] that spanwise bending moments due to the inertia of flapping wings are about twice as large as those due to aerodynamic forces. The simultaneously plotted mass distribution shows that local spanwise mass maxima appear at the wing nodus and the pterostigma. The peaks suggest that these areas have a relatively large influence on inertial deformation responses.

Fig. 8
figure 8

Mass, and maximum aerodynamic and inertial load distribution along the single wing span. Local mass and inertial load maxima appear at the wing nodes and pterostigma

Full size image

The response of the wing structure to the spatial distribution of aerodynamic and inertial loads throughout half a flapcycle are shown in Fig. 9. The wing’s angular and translational velocity is zero during stroke reversal, aerodynamic loads are therefore not present in our model. At midstroke the wing’s acceleration is zero, thus inertial loads are zero, while aerodynamic forces peak at midstroke. The peak of the aerodynamic pressure distribution is located at ±80% of the wing length. The spatial inertia distribution shows that inertial loads caused by membrane elements gradually rise to the wing tip where they reach maximum at the pterostigma (±85% r). The mass of veins causes high inertial forces from root to the tip, especially during stroke reversal when inertial loading is maximal.

Fig. 9
figure 9

Analytically modelled spatial aerodynamic pressure and inertial load distribution over the forewing area during a stroke in hovering flight. Aerodynamic load shows a spatial peak at 80% of the wing length. Due to maximal translational motion at midstroke (φ = 0°), the aerodynamic load is maximal whereas inertial loads are zero. At stroke reversal, pro- and supination, the inertial load is maximal and the aerodynamic load is zero. Vein inertial loads dominate the total inertial load

Full size image

Wing Deformation

We analyzed the wing deformation under aerodynamic and inertial loading throughout the stroke cycle for the eight loadcases shown in Fig. 6. Figure 10 shows that the wing deformation during the translational phase of the upstroke is generally 2 times higher than the deformation during downstroke. This suggests that the asymmetric wing architecture responds more stiffly against loads occurring during downstroke than during upstroke. This observation corresponds to findings of Wootton et al. [16] who show that cambered wings exhibit asymmetric bending deformations; the wing being more rigid to forces applied from the concave side than from the convex side. At supination and pronation the wing also deflects approximately 2 times more than at the midpoint of the downstroke. The difference in deformation is primarily due to the inertial loading at stroke reversal being higher than the aerodynamic loading at midstroke. Relatively small deformations are found before stroke reversal (at φ = −30° during downstroke and φ = 30° during upstroke). This is probably due to the direction of the resultant load on the wing (Fig. 6). The resultants are in these cases directed ± 15° in the plane of the wing and therefore hardly cause deformation, because the wing’s second moment of inertia is very high in this direction. The overall deformations caused by the applied loads are generally relatively small compared to the wing length. The maximum lateral displacement found is 1.5 mm which is 5.5% of the wing length and occurs during supination. Overall bending patterns are remarkably similar. Both aerodynamic and inertial load distributions induce twist towards the wingtip and increase bending of the trailing edge. The maximum twist found during supination is approximately 7°, measured at 75% of the wing length. This twist due to wing lift reduces the effective aerodynamic angle of attack of the wing, which will reduce lift and help stabilize wing deformation under aerodynamic loading.

Fig. 10
figure 10

Spatial deformations (shown 10 times enlarged) of a flapping Sympetrum vulgatum wing during hovering flight. Magenta plots show undeformed shape. (a) Deformations during downstroke. (b) Deformations during upstroke. Deformation plots during pro- and supination are similar in (a) and (b) but plotted from another point of view. Deformations during upstroke are approximately twice as large compared to the downstroke. The largest deformation is found during stroke reversal; 1.5 mm. Before stroke reversal during down- and upstroke only small deformations are found because loads are applied almost in plane of the wing (Fig. 6)

Full size image

Wing Vibration

Results of free vibration analyses, in which we neglect damping, show the same deformation for the natural modes as Wootton et al. [16] found; bending for the first natural mode and torsion for the second natural mode (Fig. 11). In our three-dimensional model these natural vibration modes occur at frequencies 4.8 (bending) and 9.3 (torsion) times higher than the insect’s flapping frequency f flap (32.3 Hz), see Table 1. In our two dimensional model (z-dimensions flattened) the first natural frequency f n (= 25.4 Hz) is close to the flapping frequency f flap (32.3 Hz) (Table 1), this result is similar to the one obtained by Wootton et al. [16].

Fig. 11
figure 11

First and second natural vibration modes of the dragonfly forewing in vacuum (top, hind and side view). (a) The first natural vibration mode of Sympetrum vulgatum. Deformation is dominated by bending. (b) The second natural vibration mode of the wing. The deformation shows mainly torsion. Green depicts the wing’s original shape

Full size image
Table 1 Natural frequencies 3D and 2D forewing
Full size table

In our two-dimensional model the deformation responses are again bending for the first mode and torsion for the second mode. Our comparison of natural vibration modes of a realistic three dimensional wing architecture and a simplified two dimensional “flat” architecture shows that the three dimensionality is critical for determining if insects flap their wings at frequencies lower, equal or higher than the resonant frequency of the wing. Our results show that Sympetrum vulgatum is flapping its forewing at a frequency roughly 5 times lower than the first bending mode and 9 times lower than first torsion mode of its forewing.

The structural and aerodynamic damping that a real wing in air will experience will lower the natural vibration frequencies we find to some degree. We estimate the reduction using the following standard equation for damped vibrating systems:

$$ {\omega_d} = {\omega_n} \cdot \sqrt {{1 - {\zeta^2}}} $$

Here, ω d is the damped natural frequency, ω n the undamped natural frequency and ζ the damping ratio. We calculate that ζ needs to be as high as 0.98 to lower the lowest natural frequency enough to make it identical to the flapping frequency. Experiments carried out by Combes and Daniel [15] with insect wings vibrating in air and helium show that damping has a minimal effect on the vibration modes of insect wings. They find that damping is only slight and primarily due to structural damping caused by material hysteresis and damping due to the fluid in the wings veins, supporting the vacuum approximation. Based on these experiments we conclude that damping coefficients of 0.98 are highly unrealistic; realistic damping ratios will be much closer to zero. Therefore we expect that our forewing vibration analysis will be realistic for dragonflies in hovering flight.

Conclusions

We found that micro-CT scanning is a very promising method for measuring and digitizing the wings, veins and membranes of insects. Whereas current state of the art micro-CT scanners are limited to large insects wings, we foresee that any insect wing could be successfully scanned in the near future as the resolution of micro-CT scanners increases every year. The main challenge for accurately digitizing the wings 3D architecture is minimizing the deformation due to drying of the wing needed to reduce scatter and noise in the scan due to evaporation. Our scan of a dragonfly Sympetrum vulgatum forewing shows that vein and membrane thickness increases from tip to root, which allows the wing to effectively bear both inertial and aerodynamic loads. Inertial loads along the wingspan are approximately 1.5–3 times higher than the aerodynamic loads. As a result the wings deformation is dominated by inertial loading, which is maximal during stroke reversal. Comparing wing deformation during up- versus downstroke we find that the wings asymmetry due to camber causes the wing being more rigid to forces applied from the concave side than from the convex side. We find that wing bending is low during hovering as the maximum lateral displacement is 5.5% wing span. Finally we find that dragonflies flap their forewing at frequencies significantly lower than the first natural vibration mode of the forewing, 5 times lower for Sympetrum vulgatum. The strategy of dragonflies to flap their wings at a much lower frequency than the natural vibration frequency of their forewing is contrasted by the most advanced flapping wings designed for micro air vehicles ([1–3]; e.g. see Fig. 1). Of these micro air vehicles the smallest ones operate at the scale of dragonflies [2]. All these flapping wing designs operate at much higher frequencies than the natural frequencies of their wing, which are extremely low because of the slack, sail-like, wing-design. These slack wings are easy to actuate back and forth and simply deform aeroelastically [3] such that the geometric angle of attack of the wing is of the right order of magnitude to generate both lift and thrust. A much stiffer wing, like the one of dragonflies, requires a more sophisticated aeroelastic design and actuation of the wings. Stiffer and more precisely designed wings could, however, yield higher performance because less energy might be dissipated due to suboptimal wing deformation and angle of attack that result from the simple sail-like wings of many flapping MAVs. In contrast, the wing deformation and angle of attack of the much stiffer dragonfly-like wings are under more precise control through high fidelity aeroelastic tailoring.