Introduction

It is common in tree breeding that selection of populations must consider conservation of genetic diversity, while at the same time attempting to maximize response to selection. It is generally recognized that one cannot simply select the “best” trees, without also taking into account the degree of relatedness among them. To ignore relatedness would result in a rapid loss of diversity in breeding populations, reducing the long-term gains possible through recurrent selection and accumulating high levels of inbreeding (Robertson 1960, 1961). Managing relatedness among selections becomes complicated as early as the first cycle of breeding, when parents, siblings, and other close relatives have similar ranks. Historically, tree breeders have often imposed rules of thumb on how many selections can be accepted from a family or other group of relatives (e.g., Jarvis et al. 1995), as well as subdivision or “sublining” of breeding populations to avoid relatedness among sublines, even as it accumulates rapidly within (e.g., McKeand and Bridgwater 1998). Such rules may be successful in regulating the accumulation of relatedness but are unlikely to result in optimal solutions that maximize gain.

The issue of how to truly optimize the balance between gain and relatedness can be approached in several ways. An optimal solution will not completely avoid kinship but rather find the set of selections that maximizes gain while imposing an overall constraint on average relatedness. In the context of tree breeding, the problem was formulated by Lindgren and Mullin (1997) who expressed “group merit” of a selected population as a function of average genetic value, penalized by a weight on relatedness among individuals, as expressed by their “group coancestry” sensu Cockerham (1967). While they provided a way to maximize group merit for a fixed number of selections with equal representation (“Group-Merit Selection”), the constraint on relatedness is applied indirectly so that achieving a specified level when selecting breeding populations requires a trial-and-error approach, typically with many iterations, and optimizing unequal numbers of ramets deployed to seed orchards is not possible.

The special case of optimizing deployment of genotypes to a seed orchard was explored by Lindgren and Matheson (1986) and Lindgren et al. (1989) who suggested that the optimum relationship between candidate breeding value and their contribution to the population would be linear. The application of “linear deployment” is only possible when the candidates are unrelated as might be the case when selecting “backward” on progeny tested plus tree candidates. If the candidate pool includes relatives, Bondesson and Lindgren (1993) suggested that a more complex formulation would be required, perhaps using a LaGrange function. In more recent work, Lindgren's group used the Microsoft Excel add-in tool, “Solver”, to maximize gain by linear programming under a LaGrange equality constraint on relatedness (Danusevičius and Lindgren 2008; Lindgren et al. 2009).

The quadratic object function was introduced by Meuwissen (1997) as the basis for seeking an optimal balance between genetic merit and relatedness by simultaneous selection of parents and calculation of their respective mating proportions. Meuwissen's algorithm is based on LaGrangian multipliers (LM) and has been used in both theoretical and practical applications to optimize breeding programs, mainly in an animal-breeding framework (e.g., Grundy et al. 1998; Avendaño et al. 2004; Hinrichs et al. 2006; Villanueva et al. 2006; Woolliams 2007; Hinrichs and Meuwissen 2011). The LM method was recommended for application to forest trees by Kerr et al. (1998) and subsequently demonstrated in the management of breeding (Hallander and Waldmann 2009a) and in the optimal selection of Scots pine (Pinus sylvestris L.) parents for a seed orchard with unequal numbers of ramets (Hallander and Waldmann 2009b). A general assumption made by LM is that the optimal solution should occur when the restriction on relatedness is exactly achieved, i.e., the optimal solution is found at the boundary of all possible solutions. After a primary solution is obtained, some candidates will obtain negative contributions as there is no restriction on the minimum (or maximum) contribution of the selection candidates. By removing negatively contributing candidates from the selection process, either all simultaneously or one-by-one, and resolving the optimization, a final set of candidates and their respective contributions is obtained.

There are, as pointed out by Pong-Wong and Woolliams (2007), some serious drawbacks with the LM method. First, by removing candidates or fixing their contributions to zero and re-optimizing with a new subset of candidates, it is possible that the true optimum solution is bypassed in the iterative procedure. Second, there is no restriction on the maximum allowed contribution of any particular candidate. This means that ad hoc manipulations of the final solution may be required to satisfy other operational constraints on its implementation. For example, in forest tree breeding, one major constraint for the establishment of grafted seed orchards is the number of scions that can be collected from a given genotype.

In this paper, we examine the application of semidefinite programming (SDP) to optimize selection for gain with a quadratic constraint on relatedness as applied to typical situations in establishment and management of forest tree seed orchards. SDP was introduced by Pong-Wong and Woolliams (2007) as an alternative method for finding a solution to a convex optimization problem in an animal-breeding framework. They reported that in several examples, SDP found a more optimal solution than did the LM approach. To our knowledge, theirs is the only published study with a focus on breeding that has utilized SDP to obtain optimal contributions although their comparisons of the SDP and LM approaches were limited to small “toy” examples. Here, we apply SDP to two illustrative case studies: (1) a real Scots pine (P. sylvestris L.) pedigree and associated breeding value estimates to illustrate the performance and flexibility of the method, while imposing additional operational constraints of interest to orchard managers and (2) selection for an elite orchard among clonally replicated loblolly pine (P. taeda L.) in a publically available pedigree representing varying degrees of relatedness among candidates.

Theoretical development and methods

Semidefinite programming

Semidefinite programming is an optimization method to minimize a linear objective function subject to the constraint that a linear combination of symmetric matrices is positively semidefinite (Vandenberghe and Boyd 1996). The constraint is convex, which means that if two points satisfy the constraint, then any point on the segment between the two points also satisfies the constraint. It is the convex nature of constraints that allows SDPs to be solved efficiently. The objective to find a minimum for a linear function over a linear matrix inequality can be described by the general form:

$$ \mathrm{Minimize}:{\displaystyle \sum_{i=1}^Z{f}_i{x}_i\kern1em \mathrm{Subject}\kern0.5em \mathrm{to}}:\kern0.5em {\mathbf{Y}}_{\mathbf{0}}-{\displaystyle \sum_{i=1}^Z{\mathbf{Y}}_i{x}_i}\ge \mathbf{0} $$

The input data are f 1, f 2, …, f Z  ∈ R and Y 0, Y 1, …, Y Z being matrices of the same dimension, while the decision variable is x ∈ R Z. The notation Y ≥ 0 indicates that matrix Y is positive semidefinite, i.e., all the eigenvalues of Y are non-negative. SDP can be considered as an extension of linear programming to the space of matrices.

The main advantage of SDP is that optimization theory guarantees the optimum solution which is found in an efficient and smooth way (Vandenberghe and Boyd 1996). SDP can be efficiently solved using interior-point methods, which are well understood and perform well in practice (Nesterov and Todd 1997; Kojima et al. 1997; Alizadeh et al. 1998). In addition, interior-point methods have the ability to exploit the structure of the optimization problem, such as the usage of sparse equation solvers. Many computer programs based on interior-point methods are available for solving SDPs, including semidefinite programming algorithm (SDPA) (Yamashita et al. 2003, 2010, 2012).

Object function formulation

To formulate the selection of genotypes with unequal numbers of ramets to a grafted seed orchard as an SDP, we first consider selecting a cohort from a complex pedigree, containing totally Z genotypes that are to contribute their genes in optimal proportions. The object is to maximize the expected genetic merit of contributions from the selected cohort, given by c T g, where the estimated breeding values (EBV) for all pedigree members are found in vector g, of size Z×1, and the contribution of genes as a proportion is denoted c, also of size Z × 1. In our problem, the decision variable is c, where 1 ≥ c i  ≥ 0, and the sum of all contributions from the selected cohort equals unity (∑ i = 1 Z c i  = 1).

There are a number of constraints required to fully formulate the selection problem. First, we wish to impose a quadratic restriction on the relatedness or group coancestry, θ, of the selected cohort, specified as θ ≥ c T Ac/2, where the additive or numerator relationship matrix of the pedigree is denoted A, of size Z × Z. The maximum and minimum contributions that a particular individual can make are denoted m and u, respectively, and both vectors are of size Z × 1. Here, if pedigree member i is not itself a candidate for selection (e.g., not physically available for use), the corresponding maximum contribution is set to zero (i.e., m i  = 0). Similarly, while the minimum number of contributions for a genotype might normally be zero, there may be times when prior investments might motivate setting u i to a specific value greater than zero, provided that m i  ≥ u i . In monecious tree species, where individuals can have reproductive structures for both genders, there are no limits imposed by gender and the total sum of all contributions in the pedigree should equal unity. For dioecious tree species, restrictions on the contribution of the separate genders are needed: c T d = 0.5 and c T s = 0.5 for female and male contributions, respectively, where: d and s are indicator vectors of size Z × 1,  d i  = 1 and s i  = 0 if tree i is a female and vice versa if i is a male.

In order to find the optimal gene contributions, the problem can be formulated as:

$$ \mathrm{Maximize}:\kern0.5em {\mathbf{c}}^T\mathbf{g} $$
(1a)
$$ \mathrm{Subject}\kern0.5em \mathrm{to}:\kern0.5em {\mathbf{c}}^T\mathbf{Ac}/2\le \theta $$
(1b)
$$ {\mathbf{c}}^T\mathbf{1}=1 $$
(1c)
$$ \mathbf{c}\ge \mathbf{u} $$
(1d)
$$ \mathbf{c}\le \mathbf{m} $$
(1e)

where 1 is a vector of size Z × 1 containing 1s. This formulation of the optimization problem is flexible; for example (1c) could easily be replaced with c T s = 0.5 and c T d = 0.5, if required to account separately for gender.

When reformulating as an SDP problem, the quadratic constraint (1b) is expressed in linear form using its Shur complement and the equality constraint (1c) replaced by two inequality constraints so that the selection problem for a monecious species is reformulated:

$$ \mathrm{Minimize}:\kern0.5em {-\mathbf{c}}^T\mathbf{g} $$
(2a)
$$ \mathrm{Subject}\kern0.5em \mathrm{to}:\kern0.5em \left[\begin{array}{cc}\hfill {\mathbf{A}}^{-1}\hfill & \hfill \mathbf{c}\hfill \\ {}\hfill {\mathbf{c}}^T\hfill & \hfill 2\theta \hfill \end{array}\right]\ge \mathbf{0} $$
(2b)
$$ {\mathbf{c}}^T\mathbf{1}-1\ge 0 $$
(2c)
$$ -{\mathbf{c}}^T\mathbf{1}+1\ge 0 $$
(2d)
$$ \mathbf{c}-\mathbf{u}\ge 0 $$
(2e)
$$ \mathbf{m}-\mathbf{c}\ge 0 $$
(2f)

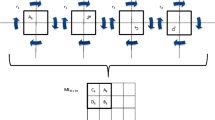
We can now formulate the results in \( \mathbf{Y}={\mathbf{Y}}_{\mathbf{0}}-{\displaystyle \sum_{i=1}^Z}{\mathbf{Y}}_i{\mathbf{c}}_i: \)

$$ \mathbf{Y}=\left[\begin{array}{ccccc}\hfill \left[\begin{array}{cc}\hfill {\mathbf{A}}^{-1}\hfill & \hfill \mathbf{c}\hfill \\ {}\hfill {\mathbf{c}}^T\hfill & \hfill 2\theta \hfill \end{array}\right]\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill {\mathbf{c}}^T\mathbf{1}-1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill -{\mathbf{c}}^T\mathbf{1}+1\hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \left[\mathbf{diag}\left(\mathbf{c}-\mathbf{u}\right)\right]\hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \left[\mathbf{diag}\left(\mathbf{m}-\mathbf{c}\right)\right]\hfill \end{array}\right]\ge \mathbf{0} $$
(3a)

with the Z + 1 set of affine matrices being:

$$ {\mathbf{Y}}_0=\left[\begin{array}{ccccc}\hfill \left[\begin{array}{cc}\hfill {-\mathbf{A}}^{-1}\hfill & \hfill {\mathbf{0}}_{\left(Z\times 1\right)}\hfill \\ {}\hfill {\mathbf{0}}_{\left(1\times Z\right)}\hfill & \hfill -2\theta \hfill \end{array}\right]\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \left[\mathbf{diag}\left(\mathbf{u}\right)\right]\hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \left[-\mathbf{diag}\left(\mathbf{m}\right)\right]\hfill \end{array}\right]\ge \mathbf{0} $$
(3b)

and

$$ {\mathbf{Y}}_i=\left[\begin{array}{ccccc}\hfill \left[\begin{array}{cc}\hfill {\mathbf{0}}_{\left(Z\times Z\right)}\hfill & \hfill {\mathbf{I}}_i\hfill \\ {}\hfill {\mathbf{I}}_i{}^T\hfill & \hfill 0\hfill \end{array}\right]\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill 1\hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill -1\hfill & \hfill \hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \left[\mathbf{diag}\left({\mathbf{I}}_i\right)\right]\hfill & \hfill \hfill \\ {}\hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \left[-\mathbf{diag}\left({\mathbf{I}}_i\right)\right]\hfill \end{array}\right]\ge \mathbf{0},i=1,2,\dots Z $$
(3c)

where the size of the first block is (Z + 1) × (Z + 1), the next two are 1 × 1, and the last two blocks are of size Z × Z.  I i is the i column of the identity matrix of size Z × Z, and diag(I i ) is a diagonal matrix with diagonal equal to I i . All other matrix elements are zero.

Solving the SDP

SDPAFootnote 1 is an open-source solver that can be applied to many types of SDPs. SDPA is very flexible, but with flexibility comes complexity and room for error, both in setting up the SDP properly and interpreting the output. We have simplified this task by embedding the SDPA solver in a user-friendly open-source tool, known as OPSELFootnote 2 (Mullin et al. 2013), which is designed specifically for such selection optimization applications in tree breeding. OPSEL receives input regarding the total number of ramets to be established in the orchard, the constraint on relatedness (as group coancestry or Status Number), whether a minimum is to be imposed on individual genotype contributions (i.e., u ≠ 0), and the name of a text file containing the EBVs of all candidate genotypes, their maximum (and minimum) frequency in the selected group, as well as the complete pedigree including ancestors. These data are used to prepare the SDP for solving by SDPA. Once SDPA has completed its work, OPSEL then reads the SDPA output and generates a file with the original data, as submitted in the pedigree file, and with additional columns specifying the optimum contribution as a proportion and as an integer number of ramets for each genotype.

Case study 1: establishing a Scots pine orchard in northern Sweden

To illustrate the application of SDP to optimize a seed orchard, we use the actual pedigree and breeding value data from the Scots pine breeding program in northern Sweden. The program has access to many plus tree founders (F0 generation) that have been progeny tested by open pollination and/or polycross and to the progeny of many pair crosses between the F0 parents that have been established in F1 family field tests. Comparable BLUP EBVs for the target orchard deployment region were available from the TREEPLAN® system (McRae et al. 2004), using all available field test data. The client's specification for the orchard is that it should contain a total of N = 2,800 ramets, having a status number N s ≥ 14 (sensu Lindgren et al. 1996 and equivalent to group coancestry θ ≤ 0.03571).

The first step was to perform a truncation of the candidate list to a total of 2,000 F1 genotypes, including not more than 15 per full-sib family, and their F0 parents. The complete pedigree list contained 2,045 genotypes. We then satisfied the orchard specification using three selection approaches:

  1. 1.

    Forwards selection of the best 14 unrelated F 1 candidates. By establishing 200 ramets for each of the best 14 unrelated F1 genotypes, we can establish a 2,800-tree orchard that satisfies the genetic diversity specification N s =14. Performing the selection is as simple as preparing a ranked list of the single best candidate from each F1 family and selecting from the top down, such that each candidate added to the selected group is unrelated to all previous selections.

  2. 2.

    Optimum selection with unequal contributions and no maximum. Here, we apply selection across all F0 and F1 candidates, while constraining on group coancestry θ ≤ 0.03571 but with no maximum contribution from any given candidate. This optimization can be solved by Meuwissen's LM algorithm or by OPSEL based on an SDP solved by SDPA.

  3. 3.

    Optimum selection with constraint on maximum contribution from F 1 genotypes. Whereas the F0 candidates are large mature trees that can contribute very large quantities of scions for grafting, the younger F1 candidates are much smaller. Practically speaking, the F1 trees are not likely capable of contributing more than 50 scions each. OPSEL can include this additional constraint in the SDP.

Case study 2: optimizing selection in a clonally replicated test of loblolly pine

Resende et al. (2012) recently made a standard set of data available onlineFootnote 3 from a clonally replicated population of loblolly pine in the southeastern USA. The population was derived by controlled crossing among 32 selected parents from the Lower Gulf Elite Population, consisting of 22 field-selected F0 plus trees and 10 selected F1 progeny. These parents were crossed in a partial diallel mating design, and the progeny propagated for field testing as rooted cuttings (Baltunis et al. 2007a, b). For this case study, we developed the SDP to optimize the selection of a grafted elite seed orchard with a total of N = 2,000 ramets, based on the published 6-year height EBVs for 861 of the candidate genotypes. The candidates together had a status number N s  = 23.3, reflecting the considerable relatedness among the clones. Contributions to the seed orchard were constrained to status number N s ≥ 10 (group coancestry θ ≤ 0.05). There were no other limitations placed on the contributions from any given genotype. The selection optimized by means of an SDP is compared with selecting the ten top-ranked, unrelated genotypes.

Results and discussion

The Scots pine case study

The case study illustrates several of the computational and operational issues faced when attempting to optimize a real orchard (Fig. 1 and Table 1). The simplest approach, (1) Forwards the selection of best unrelated F1 candidates, successfully achieves the target status number, but requires that each of the 14 selected genotypes produce 200 successful grafts. Most of the young F1 selections could not produce that many scions in a single collection, and it would take several years to completely establish the orchard by returning to the ortets in future years or collecting scion material from the earlier grafts. We also see in Fig. 1 the not unusual situation where the very best genotype is far better than average. The two parents of this genotype themselves would be good candidates for selection, but since we apply a strict restriction on inclusion of half-sib or other relatives, we are forced to go well down the candidate list to find the next eligible, unrelated genotype.

Fig. 1
figure 1

Distribution of numbers of ramets established versus estimated breeding value for genotypes selected by each method for case study 1 on Scots pine

Full size image
Table 1 Comparison of selection methods for case study 1
Full size table

In this particular example, optimization by LM or by solving the SDP gives identical results, provided that there is no constraint on the numbers of ramets contributed by any given genotype. Given that there are various degrees of coancestry between candidates, the relationship between contribution and EBV was very weak (Fig. 1), in contrast to the strong linear relationship that would be expected had the candidates been unrelated (Lindgren et al. 1989). The optimum solution in this example, where no constraints were placed on maximum contributions, utilized 56 genotypes, many of them related to each other, but still producing the required status number for the orchard. The average EBV was over 17 % greater than that from selecting 14 unrelated candidates (Table 1).

While the improvement in gain is impressive, we are still left with many F1 genotypes having to contribute very large numbers of scions that are simply not available on these smaller trees. The ability to constrain on maximum numbers of ramets is available through SDP, and the final approach applied a constraint of 50 ramets from F1 candidates, while no restriction was imposed on the numbers of ramets from F0 candidates.

The loblolly pine case study

The second case study illustrates the use of SDP to optimize selection when there is more relatedness among the candidates. Having a status number of N s =23.3, the relationships among the tested clones vary considerably, with coancestry between related clones from 0.0313 to 0.25. Selection of the top ten unrelated genotypes, each to be deployed in equal numbers, requires that we go well down the candidate list, and the orchard-wide average EBV for 6-year height is 89.0 (Table 2). Solving the SDP gives an optimum solution with 30 genotypes, each contributing from 1 to 289 ramets, distributed as shown in Fig. 2, and producing an average EBV of 114.0, over 28 % higher than deploying the top ten unrelated clones.

Table 2 Comparison of selection methods for case study 2
Full size table
Fig. 2
figure 2

Distribution of numbers of ramets versus estimated breeding value for case study 2, comparing simple selection of the top ten unrelated genotypes deployed equally with selection by SDP to optimize contributions to a 2,000-ramet loblolly pine seed orchard

Full size image

While the number of candidates is relatively small, this example illustrates the difficulty of avoiding relatedness after only 2 or 3 cycles of breeding. Solving the problem with an SDP maximizes the genetic value of the orchard, while satisfying the constraint on relatedness.

Resource requirements

A comparison of computing efficiency between the LM algorithm and OPSEL's solution by SDPA is not really possible as there exists no public access to LM software that is truly optimized. It can be noted that the time on a typical office computer to optimize selection by SDPA for the case study examples presented here is a matter of minutes. The solution for a longer candidate list of 12,000 genotypes plus ancestors used all available memory in a 16-Gb machine under Windows 7 but was completed in just over 5 h. Practically speaking, breeders would want to truncate their candidate list to avoid exceedingly long execution times.

When to optimize or re-optimize?

There are several points in the process of establishing and managing a seed orchard when a manager might wish to optimize:

  1. 1.

    Planning the initial makeup of an orchard. This is an obvious time when one would want to prepare a list of genotypes and contributions to plan the establishment of N grafted plants in an orchard.

  2. 2.

    After collection of scions, to prepare the nursery's grafting list. Typically, the scion collection operation will require a crew to visit the ortets in the field or to make collections from ramets established in clone banks or other orchards. Some donor plants will produce more than enough scion material, whereas others may fall well short of the number prescribed by the initial optimization. Some donors may be dead or too remote to allow access during the collection period. Furthermore, the grafting operation would normally prepare excess numbers of rootstock, and the grafting list should be optimized for this larger number of plants. Once the scion collection has been completed, the optimization can be rerun, using the actual numbers of scions available as the new constraint on maximum contribution and with N set to the total number of rootstock to be grafted in the nursery.

  3. 3.

    Before shipping surviving grafts to the orchard site. The nursery inventory of surviving grafts supplies the information for the maximum possible contribution of each genotype as the grafts are shipped for establishment in the orchard.

  4. 4.

    Thinning an orchard. Most orchards will require thinning at some point in their development. Updated EBVs will likely be available, while the current inventory of surviving ramets provides the constraint on the maximum numbers of ramets to be left. The desired census number after thinning provides the total number of contributions, N.

  5. 5.

    Adding material to an existing orchard. It is not uncommon for the establishment of an orchard to begin with only a portion of the total number of trees, leaving gaps for future planting. To optimize the filling in of this orchard, the existing inventory of established grafts is used as the constraint on minimum contributions, while the maximum for these genotypes must be at least as large as the minimum. N is declared as the total size of the orchard, including the preexisting material. The same approach can be used to optimize the replacement of mortality.

  6. 6.

    Optimizing an orchard when “standard” genotypes are included. There are situations when an orchard manager will want to ensure that certain genotypes are included in the orchard. These “standards” may represent genotypes whose performance or response to orchard management is well known, or there may be a known market for their seeds. Whatever is the reason for their inclusion, a constraint on the minimum contribution from these genotypes can be declared when the orchard is optimized.

SDP for optimizing seed mixtures from orchards

Of course, the optimizing of seed orchard establishment around a constraint on relatedness assumes that each ramet of the various candidate genotypes will contribute the same number of gametes to the seed produced in the orchard. This may be a reasonable assumption for many open-pollinated orchard species but will certainly not be the case when fertility varies greatly among genotypes or when seed is produced by controlled crossing. SDP can still be useful in such situations by optimizing the mixing of seedlots collected in the orchard, providing high genetic value while satisfying a constraint on status number.