Predictive control of irrigation canals – robust design and real-time implementation

Abstract

Predictive control is one of the most commonly used control methods in a variety of application areas, including hydraulic processes such as water distribution canals for irrigation. This article presents the design and application of predictive control for the water discharge entering into an irrigation canal located in Spain. First, a discrete time linear model of the process is described and its parameters are experimentally identified. The model is well validated within the usual canal operating range and is used to formulate a predictive control law with an incremental formulation. Finally, experimental and simulation results are presented in which predictive control has shown better performance than a well-tuned proportional, integral and derivative controller to automatically manage demanded water discharges.

1 Introduction

Agriculture consumes between 75 % an 80 % of the world’s freshwater resources, its availability is constantly decreasing and its use will probably be a source of important conflicts. For this reason the modern, efficient and sustainable management of the hydrologic resources is crucial. In this process, automatic control has an important role (Rodellar et al. 1989; Schuurmans and Maherani 1991). The control policies in the large distributor canals can be classified as follows: (i) according to the controlled variable, discharge or water level control; (ii) according to the control action variables, discharge or gate opening; and (iii) according to the location of the controlled variable, upstream control or downstream control (Malaterre et al. 1998). Though these processes are mainly non-linear and have large time delays, their dynamic behaviour can locally be approximated with linear equations containing time-dependent parameters.

Predictive control (PC), after Proportional Integral Derivative (PID) control, is one of the most commonly used control methods in different industrial processes. PC encompasses a group of algorithms having the following common characteristics: (i) explicit use of a model to calculate the predicted output in a future time horizon; (ii) calculation of the control action through the minimization of a certain cost function; and (iii) use of a receding horizon strategy: at each control instant, only the first step of the calculated control action is applied, the rest is not used. Then calculation is repeated while the prediction horizon is shifted one step forward (Martín Sánchez and Rodellar 2014).

The main advantage of PC over other control methods is its ability to control a wide variety of processes, from the simplest to more complex ones, including systems exhibiting big time delays, non-minimal phase systems, unstable systems, mono and multivariable systems. When the cost function is not formally restricted and the predictive model is linear, the minimization problem has analytical solution, thus resulting into simple control laws easy to implement. In the case of constraints, there is no analytical solution of the cost function and the minimization has to rely on numerical approaches such as quadratic programming (Hashemy Shahdany et al. 2015). This can be a drawback of PC, especially when it has to be implemented in practice via Programmable Logic Controllers (PLC), since they are usually designed to carry out elementary mathematical operations. In the same vein, non-linear complex models may also require numerical solutions where bad conditioned problems may arise. A practical preference, when the process and the equipment allow it, is to use simplified models with a linear structure. In such a case, models can be obtained through system identification and parameter adaptation and/or robustness issues have to be considered to ensure the control effectiveness.

In this paper, a linear predictive control scheme is presented and implemented in a field irrigation canal, which relies on an identified linear model. From the end of the 1980s, different authors used predictive control of water levels or discharges in irrigation canals. In these first works only simulation results are shown and only single input-single output processes are considered. The control law is calculated from a particular solution of the extended predictive control strategy, which minimizes the cost function only at the end of the prediction horizon. They also consider constant control action and they do not use constraints (Rodellar et al. 1989, 1993; Akouz et al. 1998; Sawadogo et al. 1998; Gómez et al. 2002). In (Malaterre and Rodellar 1997) the predictive control is applied to a multivariable system and the cost function is minimized over a prediction horizon. In (Wahlin 2004) constraints on the cost function are also considered and the predictive control is tested on a numerical benchmark canal. In (Rivas et al. 2002), an adaptive predictive control is considered. In (Soler et al. 2008) predictive control with constraints is applied in open loop to schedule optimal gate trajectories. This scheme is further extended in (Soler et al. 2013). Predictive control with multiple models is applied in (van Overloop et al. 2008) to drainage canals and in (Delgoda et al. 2013) for regulated river systems.

Implementations of predictive control in small-scale laboratory canals have been reported for instance in (Begovich et al. 2004), using multivariable model predictive control with constraints. In (Silva et al. 2007) predictive control is implemented in a testing canal using a model obtained from the linearization of the Saint Venant equations. Finally in (Sepúlveda 2007) a multivariable predictive control scheme in a three-reach laboratory canal is presented where the model is obtained with identification techniques. The same canal is used in (Horváth et al. 2015a, b) to assess redictive controllers using simplified models for control of levels in the presence of disturbances.

Finally, it is important to mention that there are only few published studies about predictive control in large irrigation canals. In (van Overloop et al. 2010) a multivariable constrained controller was first tested in an 8-reach irrigation canal. In (Sadowska et al. 2014) a hierarchical water level control scheme was applied on a large-scale irrigation canal. Most of the proposed works in the literature use theoretic models derived from linear simplifications of the Saint-Venant equations around operating points. Examples are the Muskingum model (Cunge 1969), which is often used for hydrologic routing, the Hayami hydraulic model (Hayami 1951) and the integrator plus delay model (Schuurmans 1995). The use of these models might not always provide the best choice in case of large canals where little information may be available about the geometry of the canal.

The following papers describe implementations of adaptive predictive expert controllers in field irrigation canals: (Aguilar et al. 2009, 2012; Langarita 2010). They design single input-single-output controllers for discharges and water levels based on a particular solution of the extended predictive control strategy (Martín-Sánchez and Rodellar 2014). Initial nominal models of the canal are obtained by in-field system identification and further on-line parameter adaptation is used to accommodate the controller to changes in the operating conditions.

The approach followed in this paper lies within the same scheme as in (Aguilar et al. 2009, 2012), since a nominal model is obtained by system identification from the real canal. But, instead of adding on-line parameter adaptation, this work contributes with a controller designed with fixed parameters to operate within an expected range in the operating flow conditions. The controller is implemented, using the existing facilities, to control the discharge entering into a distribution canal for irrigation in the northeast of Spain. A well-tuned discrete time PID controller is also used for comparative purposes.

2 Problem statement

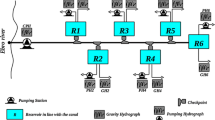
The objective is to control the discharge entering to the origin of the Zaidín Canal, which is located 32 Km downstream of the Canal de Aragón/Catalunya main course in the northeast part of Spain. Zaidín Canal is 54 Km long, it has a longitudinal mean slope of 4/1000 and has a trapezoidal cross section. The operational discharge fluctuates between 2 and 20 m ³/s, being able to deliver a maximum of 25 m ³/s. It is managed mainly for irrigation water distribution, although it also delivers water for a population of 10,000 people. Figure 1 shows the hydraulic scheme in the origin of the canal.

Fig. 1

Hydraulic scheme of the origin of the Zaidín Canal under study

The control action variable is the gate opening, which varies between 0 and 330 cm. It is implemented through a system of three gates (C) with electronic motors. The controlled variable is the discharge (Q) 120 m downstream the gates and it varies between 2 and 20 m ³/s. The hydraulic structure at the origin of the canal has two important characteristics: (i) there is a control loop (C1) for the water level (L) upstream the gates, so that the flow over the gates is constant (this part is not object of this work); and (ii) the gates are free flow gates, that is, the downstream hydraulic jump never gets submerged. Due to these two conditions, the discharge through the gates only depends on the gate openings. Therefore, it is expected that the process dynamics will not exhibit large changes within the whole possible discharge range. In this scenario, the problem is stated to design and physically implement a predictive controller without adaptive capability, this means using a model with fixed parameters, but designing the controller to be effective within the operation discharge range.

Before the installation of the control system, the canal was under manual management: an operator was in duty 24 h/day all the year long and checked the entering discharge every hour, making deviation corrections by manipulating the upstream gates. Usually, discharge errors of 2 % were allowed during long time periods, what resulted into 400 l/s, which is a significant amount. The implementation of automatic control has led to a drastic reduction in such discharge errors and alleviated the need of a permanent presence of operators, which may be in charge of different tasks.

3 Methods

The work follows two main steps:

• 1. A nominal model of the plant is obtained through system identification using real input–output data.

• 2. A predictive control law with fixed parameters is formulated to generate the gate openings and is programmed into a commercial PLC and implemented in the field

3.1 Modelling and system identification

In order to design effective control systems - especially when the model is also used for prediction – mathematical models are needed to describe the dynamic relations between the process variables. Traditionally, irrigation canals are modelled by the Saint Venant equations (Chow 1988). They are a set of hyperbolic quasi-linear partial second order differential equations based on open channel flow physical laws, which are solved using numerical procedures. These numerical solutions are very useful for simulation purposes but they are not suitable for control design due to their complexity and computational cost. For this reason, simplified dynamic models are usually adopted for control purposes, which can be divided into two categories: (i) linearization of the Saint Venant equations and use of simplified hydrologic laws; and (ii) use of black box models whose parameters are determined through system identification. In cases where not enough information about the canal geometry is available and field identification tests are feasible, the second option is a possible and practical alternative. This is the approach followed in this work.

The input–output relationship of a single input-single output non-linear process can be described as a linear parameter-varying equation around and operation point in the following discrete time form:

$$ y(k)={\displaystyle \sum_{i=1}^n{a}_i(k)y\left(k-i\right)+{\displaystyle \sum_{i=1}^m{b}_i(k)u\left(k-r-i\right)+\varDelta (k)}} $$

(1)

where k is an integer number denoting the time step, so that the physical time is t = kT, using a sampling period T. Variables u and y are measured values of the process input and output, respectively, r is the time delay expressed in sampling periods, a _i  , b _i are parameters that are usually unknown and time varying, and n and m are integers defining the model order. ∆(k) is a perturbation signal that groups the combined effect of non-measurable disturbances, measurement noise and unmodelled dynamics.

In this work, we obtain a model with the structure in (1), but with constant parameters, to represent the canal dynamics around a specific operation point, which is characterized by a steady state water discharge. The input u is the upstream gate opening and the output y is the downstream discharge. Two types of experimental identification tests are carried out for this purpose: (1) a step response test, where the discharge is measured when the upstream gate is opened or closed; and (2) a test where the gate is manipulated using a pseudo-random binary sequence (PRBS). The first step response tests allow to estimate the gains, delays main time constants at different operational points. The second test is used for the validation of the models obtained with the step response test at high frequencies (Rivera 1992).

3.2 Predictive control law

The background of the control strategy adopted in this work can be found in (Martín-Sánchez and Rodellar 2014). It is based on two main premises: (1) at each real time instant k, a prediction horizon [k, k + λ] is considered for a number of λ future time instants, where a sequence of process outputs $\widehat{y}\left(k+j\left|k\right.\right)$ is predicted by a model depending on a sequence of control inputs $\widehat{\hat{u}}\left(k+j-1\left|k\right.\right)$; and (2) the control sequence is derived through the minimization of a cost function.

In this case, the following predictive model is adopted:

$$ \begin{array}{l}\varDelta \hat{y}\left(k+j\left|k\right.\right)={\displaystyle \sum_{i=1}^n{\hat{a}}_i\varDelta \hat{y}\left(k+j-1\left|k\right.\right)+{\displaystyle \sum_{i=1}^m{\hat{b}}_i\varDelta}\widehat{\hat{u}}\left(k+j-1\left|k\right.\right)}\\ {}\\ {}j=1,2....,\lambda \\ {}\varDelta \widehat{\hat{y}}\left(k+j\left|k\right.\right)=\widehat{\hat{y}}\left(k+j\left|k\right.\right)-\widehat{\hat{y}}\left(k+j-1\left|k\right.\right)\\ {}\varDelta \widehat{\hat{u}}\left(k+j\left|k\right.\right)=\widehat{\hat{u}}\left(k+j\left|k\right.\right)-\widehat{u}\left(k+j-1\left|k\right.\right)\\ {}\varDelta \widehat{\hat{y}}\left(k+1-i\left|k\right.\right)=\hat{y}\left(k+1-i\right)-\hat{y}\left(k-1\right)\kern1.2em i=1,..,n\\ {}\varDelta \widehat{\hat{u}}\left(k+1-i\left|k\right.\right)=\hat{u}\left(k+1-i\right)-\hat{u}\left(k-1\right)\kern1.32em i=1,..,m\end{array} $$

(2)

Note that this model uses the increments of the input and output variables and that the model is redefined at each real time instant k from the actual and previous measured values u and y. Increments are convenient to avoid permanent offsets in the controlled steady state setpoints (Horváth et al. 2015b), while the redefinition allows to perform the on-line minimization using the last updated measured feedback information, which is relevant to add robustness to the control law against modelling and measurement errors and unknown disturbances. Model (2) can be written in a recursive form as follows:

$$ \begin{array}{l}\varDelta \widehat{\hat{y}}\left(k+j\left|k\right.\right)={\displaystyle \sum_{i=1}^n{\hat{e}}_i^{(j)}\varDelta y\left(k+1-i\right)+{\displaystyle \sum_{i=2}^m{\hat{g}}_i^{(j)}\varDelta \hat{u}\left(k+1-i\right)+}}\\ {}+{\displaystyle \sum_{i=0}^{j-1}{\hat{g}}_1^{\left(j-i\right)}}\varDelta \hat{u}\left(k+i\left|k\right.\right)\\ {}\\ {}{\hat{e}}_i^{(1)}={\hat{a}}_i;\kern0.5em {\hat{g}}_{n+1}^{\left(j-1\right)}=0;\\ {}{\hat{e}}_i^{(1)}={\hat{e}}_1^{\left(j-1\right)}{\widehat{a}}_i+{\hat{e}}_{i+1}^{\left(j-1\right)}\kern2.28em i=1,..,n;\kern0.6em j=2,\dots, \lambda \\ {}{\hat{g}}_i^{(1)}={\hat{b}}_i;\begin{array}{cc}\hfill \hfill & \hfill {\hat{g}}_{m+1}^{\left(j-1\right)}=0\hfill \end{array};\\ {}{\hat{g}}_i^{(j)}={\hat{e}}_1^{\left(j-1\right)}{\widehat{b}}_i+{\hat{g}}_{i+1}^{\left(j-1\right)}\kern2.04em i=1,..,n;\kern0.6em j=2,\dots, \lambda \end{array} $$

(3)

The advantage of this model is that the predicted increments $\varDelta \hat{y}\left(k+j|k\right)$ are explicitly given in terms of the measured input–output increments Δu(k + 1 − i) and Δy(k + 1 − i) and the unknown future control inputs $\varDelta \hat{u}\left(k+i|k\right)$.

The following linear quadratic cost function is used:

$$ {J}_k=\frac{1}{2}{\displaystyle \sum_{j=1}^{\lambda }{Q}_j{\left[\widehat{y}\left(k+j\left|k\right.\right)-{y}_r\left(k+j\left|k\right.\right)\right]}^2+\frac{1}{2}{\displaystyle \sum_{j=0}^{\lambda -1}{R}_j\varDelta \hat{u}{\left(k+\left.j\right|k\right)}^2}} $$

(4)

where Q _j  , R _j are weighting parameters and y _r is a reference trajectory defined in the following form:

$$ \begin{array}{l}{y}_r\left(k+j\left|k\right.=\right){\displaystyle \sum_{i=1}^p{\alpha}_i{y}_r\left(k+j-i\left|k\right.\right)}+{\displaystyle \sum_{i=1}^w{\beta}_i{y}_{sp}\left(k+j-i\right)}\\ {}{y}_r\left(k+1-i\left|k\right.\right)=y\left(k+1-i\right)\kern2.04em i=1,..,p\end{array} $$

(5)

where y _sp is the prescribed setpoint (constant during the whole prediction horizon) and α _i  , β _i are design parameters characterising the reference dynamics. The minimization of J _k results into the following control law:

$$ \begin{array}{l}\varDelta u(k)=-\left[{\displaystyle \sum_{i=1}^{\lambda }{g}_i}\right]y(k)-{\displaystyle \sum_{i=1}^n{\widehat{g}}_0^T{\widehat{E}}_i\varDelta y\left(k+1-i\right)}\\ {}{\displaystyle \sum^{m-1}{\widehat{g}}_0^T{\widehat{G}}_i\varDelta u\left(k-i\right)+\left[{\displaystyle \sum_{i=1}^{\lambda }{g}_i}\right]}{y}_{sp}(k)\\ {}u(k)=u\left(k-1\right)+\varDelta u(k)\end{array} $$

(6)

Note that this expression gives the control u(k) to be applied at instant k using the measured output y(k) and the prescribed setpoint y _sp (k). The parameters involved in (6) are obtained from the parameters given in (3). Details are omitted here but they can be found in (Martín-Sánchez and Rodellar 2014).

4 Results

4.1 Modelling and identification

Concerning the model identification of the canal under study, step response and PBRS tests were carried out at three different operation points characterized by a steady state discharge of 5, 10 and 15 m ³/s, respectively. As an example, the analysis and the obtained results are shown below for experiments in the range of 10 m ³/s. All the results are given in deviation percentage around the steady state value. Figure 2 shows the discharge step response when a gate was opened and closed 11 cm. The step experiments were performed with a sampling time of 1 s, measuring and recording both the input gate position and the output water discharge in the commercial programmable logic controller Siemens S7–300 available in the canal facility. It can be seen that the opening and closing dynamics are very similar; they have practically the same gain, the same time constants and the same time delay. The following transfer function was obtained with good precision from these tests:

$$ G(s)=\frac{0.000174s+0.000001044}{s^3+0.0309{s}^2+0.0005056S+0.000000856}{e}^{-20s} $$

(7)

Fig. 2

Step response tests for the 10 m ³/s steady state case

It has a zero z =  − 0.006, a real pole p _r  =  − 0.0019 and two complex poles p _c  =  − 0.0145 ± 0.0155i. The static gain is G = 0.000174 and the time delay is 20 s.

Figure 3 shows the validation of the model with the data of both step response tests performed in the field.

Fig. 3

Validation of the step response tests for the 10 m ³/s steady state case

By discretizing the transfer function (7) with zero order hold and 90-s sampling time, the following model is obtained without explicit time delay:

$$ \begin{array}{l}\widehat{\hat{y}}(k)={\displaystyle \sum_{i=1}^3{\hat{a}}_iy\left(k-1\right)+}{\displaystyle \sum_{i=1}^4{\widehat{b}}_iu\left(k-1\right)}\\ {}\left[\begin{array}{c}\hfill {\widehat{a}}_i\hfill \\ {}\hfill {\widehat{b}}_i\hfill \end{array}\right]=\left[\begin{array}{c}\hfill 0.9377;-0.1535;0.06198\hfill \\ {}\hfill 0.2282;0.08208;-0.1201;-0.002533\hfill \end{array}\right]\end{array} $$

(8)

where ${\widehat{a}}_{i,}{\widehat{b}}_i$ are the estimated model parameters,$\overset{\frown }{y}$ is the estimated discharge without considering the perturbation signal, y is the real measured discharge and u is the input signal that corresponds to the position of the gates.

The behaviour of this model is further validated for high frequencies using PRBS test. From the gain, time delay and dominant time constants of the continuous model (7), the input signal (gate opening C) for the PRBS test was designed as described in (Rivera 1992). The test was implemented with a sampling time of 90 s and is shown in Fig. 4. The upper plot shows the output (discharge) and the lower one shows the PRBS input (gate opening). Figure 5 shows the results of the validation test of the discrete time model (8) using the data obtained from the PRBS.

Fig. 4

PRBS identification test: discharge (upper plot) and gate opening (lower plot)

Fig. 5

Validation of model (8) with PRBS: real and model discharges (upper plot) and error (lower plot)

The model accuracy is calculated from the validation test using the following expression (Ljung 2000):

$$ val\left(\%\right)=100\left(1-\frac{\left\Vert \widehat{\overline{y}}-\overline{y}\right\Vert }{\overline{y}-\frac{1}{k}{\displaystyle \sum_{i=1}^k{y}_i}}\right)=93.95\% $$

(9)

where $\overline{y},\widehat{\overline{y}}$ are the vectors containing the real measured and estimated discharges, respectively, and k is the number of samples.

The previous approach is repeated with the step and the PRBS tests applied for the operation points of 5 and 15 m ³/s. With the same model structure as in (8), new sets of parameters ${\widehat{a}}_i,{\widehat{b}}_i$are obtained, which are stored in a parameter $\overset{\frown }{\theta }$as follows:

$$ \overset{\frown }{\theta_5}=\left[\begin{array}{c}\hfill 0.9383\hfill \\ {}\hfill -0.1637\hfill \\ {}\hfill 0.0675\hfill \\ {}\hfill 0.2326\hfill \\ {}\hfill 0.0897\hfill \\ {}\hfill -0.1257\hfill \\ {}\hfill -0.0027\hfill \end{array}\right]\kern0.96em {\overset{\frown }{\theta}}_{15}\left[\begin{array}{c}\hfill 0.9373\hfill \\ {}\hfill -0.144\hfill \\ {}\hfill 0.0569\hfill \\ {}\hfill 0.2239\hfill \\ {}\hfill 0.0748\hfill \\ {}\hfill -0.1148\hfill \\ {}\hfill -0.0023\hfill \end{array}\right]\kern1.68em \overset{\frown }{\theta }=\left[\begin{array}{c}\hfill {\overset{\frown }{a}}_i\hfill \\ {}\hfill {\overset{\frown }{b}}_i\hfill \end{array}\right] $$

(10)

4.2 Control

This section presents the implementation of the predictive control law described in Section 3.2. The first issue is the selection of a predictive model with the structure presented in (2). Based on the experiments performed in Section 4.1, this model is the one identified in (8) for an operational steady stage discharge of 10 m ³/s. It is worth to note that the parameters (10) obtained for 5 and 15 m ³/s, respectively, have slight differences with respect to those in (8). This is in favour of using this set of parameters to design a control with a fixed structure within the operating range 5–15 m ³/s. Predictive control exhibits some degree of inherent robustness against parametric variability, as proven and discussed in (Martín-Sánchez and Rodellar 1997).

The second issue is the parameter selection in the control law (3–6): weighting factors in the cost function (4) and the number of future time steps (λ) in the prediction horizon. With Q _j  = 1 , R _j  = 0.3 and λ = 3, along with the incremental predictive model (2) with the estimated model parameters (8), the resulting control law is

$$ \begin{array}{l}\varDelta u(k)=-1.1512y(k)-1.633\varDelta y(k)+0.2392\varDelta y\left(k-1\right)-\\ {}-0.1156\varDelta y\left(k-2\right)-0.06162\varDelta u\left(k-1\right)+0.226\varDelta u\left(k-2\right)+\\ {}+0.004726\varDelta u\left(k-3\right)+1.1512{y}_{sp}(k)\\ {}\\ {}u(k)=u\left(k-1\right)+\varDelta u(k)\end{array} $$

(11)

The predictive control law (11) was programmed in a commercial programmable logic controller (PLC) Siemens S7–300, together with the restriction of minimal allowed gate movement, which was 1 cm. For comparison purposes, a proportional integral derivative (PID) control was also programmed in the PLC. The PID was designed using the AMIGO methodology (Approximated M-constrained Integral Gain Optimization) (Aström and Hägglund 2006) to obtain a satisfactory behaviour in the same operation range in which the predictive model was identified. The PID control law is the following:

$$ u(k)=u\left(k-1\right)+1.653\ e(k)-1.181\ e\left(k-1\right)+0.2778\ e\left(k-2\right) $$

(12)

where e(k) = y(k) − y _sp (k) is the error between the measured output and the setpoint.

Two tests are presented to compare both controllers in a typical operation involving a demanded setpoint change. Test 1 consists in demanding a step setpoint increase of 1 m ³/s starting from a steady state of 3 m ³/s. Test 2 seeks for a step setpoint increase of 1 m ³/s starting from a steady state of 15 m ³/s. Both experiments have in common that they are performed in scenarios close to the extremes of the discharge operating range. Figures 6 and 7 show the results of Tests 1 and 2, respectively, displaying the time histories of the controlled water discharge (Q) and the control gate opening (C).

Fig. 6

Test 1. Controlled setpoint change in a low range discharge scenario

Fig. 7

Test 2. Controlled setpoint change in a high range discharge scenario

Discharge and setpoint (upper plots) and gate opening (lower plot.

Discharge and setpoint (upper plots) and gate opening (lower plot.

Finally, Figs. 8 and 9 show the comparison between the field and the simulated results in the case of Test 1 for the predictive controller and for the PID, respectively.

Fig. 8

Test 1. Real and simulation predictive control tests

Fig. 9

Test 1. Real and simulation PID control tests

5 Discussion of the results

The intention of the modelling effort in this work is to provide a linear discrete time model with fixed parameters able to describe the input–output behaviour of the canal reach within the usual operating range. The purpose of this model is to supply real time prediction over a (short) finite time horizon as the background to derive the control law through a simple optimization problem. As a first insight, it is worth to remark the small discrepancy between the continuous model (7) and the real data observed in Fig. 3. It is around 20 l/s, which means 0.1 % of the maximum discharge within the operational range. A second remark is related to the PRBS test performed with the final discrete time model obtained in (8). In this test, the input signal was designed to have power for frequencies high enough to cover the cut-off frequency of the continuous time model. In this way, it is guaranteed that the discrete model is validated in all the closed loop bandwidth (Rivera and Gaikwad 1995). The high percentage of validation for the discrete time model (8) shown in (9) suggests that there are not significant dynamics of the process hidden in the perturbation signal Δ(k), and hence the errors shown in Fig. 5 can be reasonably attributed to the parameter variability of the process around the operation point as well as to the measurement noise.

Regarding the control performance, Figs. 6 and 7 show, qualitatively, that the predictive controller obtains better results than PDI control at the two different operation points, exhibiting less overshoot in the controlled discharge and less control effort with smaller gate excursions. To assess the capabilities of the two control techniques in more detail, three usual performance indices are calculated and given in Table 1: (i) Maximum deviation from the setpoint; (ii) settling time (t ₅₀), i.e. the time it takes for the water discharge to arrive and stay within a band of 50 l/s; and (iii) IAE: integral of the absolute error magnitude. Predictive control is more efficient in the three indicators.

Table 1 Performance indices for the field control tests

The comparisons between real and simulated results in the control Test 1 (see Figs. 8 and 9) for both controllers show a good matching. This can be also interpreted as the models identified in this work are close to the process dynamics even under closed loop control.

6 Conclusions

In this work a robust predictive discharge controller for a real irrigation canal was designed, tested and compared with a well-tuned discrete PID controller. From the presented results the following conclusions can be drawn:

• (1) The approach presented in Section 3 is appropriate to obtain a model of the plant for predictive control purposes. Indeed, the model is well validated with pseudo random binary test and the similarity between simulated and real results under the predictive control law also indicates that the identified models are close to the real process.

• (2) In practice, it is not possible to use constrains in the control objective function when the controller is to be programmed in a commercial PLC. However, when the only constraint is on the minimum change allowable in the control signal, this restriction can be directly implemented in the PLC. This allows designing a linear control law.

• (3) The field control tests have shown that the predictive control law is more efficient than a well-tuned PID control.