Abstract
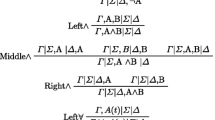
In this paper we investigate a semantics for first-order logic originally proposed by R. van Rooij to account for the idea that vague predicates are tolerant, that is, for the principle that if x is P, then y should be P whenever y is similar enough to x. The semantics, which makes use of indifference relations to model similarity, rests on the interaction of three notions of truth: the classical notion, and two dual notions simultaneously defined in terms of it, which we call tolerant truth and strict truth. We characterize the space of consequence relations definable in terms of those and discuss the kind of solution this gives to the sorites paradox. We discuss some applications of the framework to the pragmatics and psycholinguistics of vague predicates, in particular regarding judgments about borderline cases.
Article PDF
Similar content being viewed by others
Avoid common mistakes on your manuscript.
References
Alxatib, S., & Pelletier, J. (2010). The psychology of vagueness: Borderline cases and contradictions. Mind and Language. (forthcoming).
Asher, N., & Lascarides, A. (1993). Temporal interpretation, discourse relations, and commonsense entailment. Linguistics and Philosophy, 16, 437–493.
Beall, J., & van Fraassen, B. C. (2003). Possibilities and paradox: An introduction to modal and many-valued logic. Oxford: Oxford University Press.
Cobreros, P. (2008). Supervaluationism and logical consequence: A third way. Studia Logica, 90(3), 219–312.
Cobreros, P. (2010). Varzi on supervaluationism and logical consequence. Mind. (forthcoming).
Dalrymple, M., Kanazawa, M., Kim, Y., Mchombo, S., & Peters, S. (1998). Reciprocal expressions and the concept of reciprocity. Linguistics and Philosophy, 21, 159–210.
Douven, I., Decock, L., Dietz, R., & Egré, P. (2010). Vagueness: A conceptual spaces approach. (manuscript, under review).
Dummett, M. (1975). Wang’s paradox. Synthese, 30, 301–324.
Egré, P., & Bonnay, D. (2010). Vagueness, uncertainty, and degrees of clarity. Synthese, 174, 47–78.
Fine, K. (1975). Vagueness, truth, and logic. Synthese, 30, 265–300.
Goodman, N. (1951). The structure of appearance. Cambridge: Harvard University Press.
Grosz, B., Joshi, A., & Weinstein, S. (1995). Centering: A framework for modeling the local coherence of discourse. Computational Linguistics, 21, 203–226.
Hyde, D. (1997). From heaps and gaps to heaps of gluts. Mind, 106, 641–660.
Kamp, H. (1976). Two theories about adjectives. In E. L. Keenan (Ed.), Formal semantics for natural language. Cambridge: Cambridge University Press.
Kamp, H. (1981). The paradox of the heap. In U. Mönnich (Ed.), Aspects of philosophical logic. D. Reidel.
Keefe, R. (2000). Theories of vagueness. Cambridge: Cambridge University Press.
Luce, R. D. (1956). Semiorders and a theory of utility discrimination. Econometrica, 24, 178–191.
Mendelson, B. (1975). Introduction to topology (3rd ed.). Dover reedition 1990. New York: Dover.
Pawlak, Z. (2005). A treatise on rough sets. In J. F. Peters, & A. Skowron (Eds.), Transactions on rough sets IV (pp. 1–17). Berlin: Springer.
Pinkal, M. (1995). Logic and Lexicon. Dordrecht: Kluwer Academic Publishers.
Priest, G. (1979). Logic of paradox. Journal of Philosophical Logic, 8, 219–241.
Priest, G. (2008). An Introduction to non-classical logic: From if to is (2nd ed.). Cambridge: Cambridge University Press.
Ripley, D. (2009). Contradictions at the borders. In R. Nouwen, R. van Rooij, H.-C. Schmitz, & U. Sauerland (Eds.), Vagueness in communication. Berlin: LICS, Springer. (forthcoming).
Ripley, D. (2010). Sorting out the sorites. In F. Berto, E. Mares, & K. Tanaka (Eds.), Paraconsistent Logic (tentative title). (forthcoming).
Serchuk, P., Hargreaves, I., & Zach, R. (2010). Vagueness, logic and use: Four experimental studies on vagueness. Mind and Language. (forthcoming).
Smith, N. J. J. (2008). Vagueness and degrees of truth. Oxford: Oxford University Press.
Smullyan, R. M. (1995). First-order Logic. New York: Dover.
van Rooij, R. (2010a). Implicit vs. explicit comparatives. In P. Egré, & N. Klinedinst (Eds.), Vagueness and language use. Palgrave Macmillan.
van Rooij, R. (2010b). Vagueness, tolerance, and non-transitive entailment. (manuscript).
Varzi, A. (2007). Supervaluationism and its logics. Mind, 116, 633–676.
Weber, Z. (2010). A paraconsistent model of vagueness. Mind. (forthcoming).
Williamson, T. (1994). Vagueness. London: Routledge.
Winter, Y. (2001). Plural predication and the strongest meaning hypothesis. Journal of Semantics, 18, 333–365.
Zardini, E. (2008). A model of tolerance. Studia Logica, 90, 337–368.
Author information
Authors and Affiliations
Corresponding authors
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License ( https://creativecommons.org/licenses/by-nc/2.0 ), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Cobreros, P., Egré, P., Ripley, D. et al. Tolerant, Classical, Strict. J Philos Logic 41, 347–385 (2012). https://doi.org/10.1007/s10992-010-9165-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10992-010-9165-z