Capital Accumulation and Embodied Technological Progress

Abstract

This paper combines technology adoption with capital accumulation taking into account technological progress. We model this as a multi-stage optimal control problem and solve it using the corresponding maximum principle. The model with linear revenue can be solved analytically, while the model with market power is solved numerically. We obtain that investment jumps upwards right at the moment that a new technology is adopted. We find that, if the firm has market power, the firm cuts down on investment before a new technology is adopted. Furthermore, we find that larger firms adopt a new technology later.

1 Introduction

This paper aims at studying the timing of technology adoption. To do so we employ a relatively new multi-stage modeling approach [1–4] that is perfectly suitable to take into account the disruptive changes caused by innovations. This also enables us to say something about the length of the time interval that the firm invests in a particular technology, and how the technology adoption decision interacts with the firm’s capital accumulation behavior.

Our approach is mostly related to [4, 5] and more recent contributions, like [6, 7]. In these contributions, learning raises productivity of a given technology over time, and revenue is linear in the capital stock. The latter assumption prevents taking into account a decreasing returns to scale production function and market power. Especially the latter feature is crucial in today’s economy, where many industries have an oligopolistic structure. Therefore, there is a necessity to move to a model where the revenue function is strictly concave. This is certainly a technical challenge, and we study such a model in this paper.

We start out studying the simple benchmark case of a firm whose revenue is proportional to its capital stock. This implies that the firm is a price taker in the output market, and that the production function exhibits constant returns to scale. Furthermore, we assume away discounting and consider a finite planning period. The main advantage of such a simple setting is that insightful analytical results can be obtained. Because of technological progress, an adoption of a new technology means that the firm exchanges a less efficient technology for a more efficient one. For this reason, it is optimal for the investment rate to jump upwards.

We then move to the clearly innovative case, where the revenue function is concave. This is due to market power, which implies that increasing its output reduces the output price. We reintroduce discounting and take the planning period to be infinite. Like in the previous model, also here investment jumps upwards at the moment of the technology switch. As in [8], here we also find a negative anticipation effect, i.e. the firm invests less before it adopts a new technology, so that it can invest more in the new technology later on without reducing the output price too much. This accelerates replacing the old capital stock by the new one. It is important to realize that such an anticipation effect is absent in models where revenue is linear in the capital stock (like, e.g., [4] and [5]). A new finding is that a bigger firm adopts a new technology at a later point of time. The larger the capital stock, the smaller the marginal revenue, which implies that it is less profitable to switch to a more efficient technology soon. This reduces the opportunity cost of waiting with adopting the new technology, so the firm will adopt late. Again, such an effect is absent in linear revenue models like [4, 5]. The implication is that in the long term a bigger firm will produce more efficiently, which makes it optimal to grow to a higher long-run equilibrium capital stock.

The paper is organized as follows. Section 2 presents the model, while Sect. 3 analyzes the linear revenue case. Section 4 considers the firm with market power, while Sect. 5 concludes.

2 The Model

This paper makes use of a relatively new multi-stage modeling approach, see, e.g., [4] to analyze optimal decisions of technology adoption, and capital investment. In presenting the model, we impose that the firm can adopt a new technology only once. Later on we allow for multiple adoptions over time.

Denote the adoption time of the new technology by T, which is a decision variable. Following [4, 5], we introduce K(t) to be the capital stock measured in productivity units being valid at time 0. Before any switch in technology has occurred, an investment of one unit leads to an increase of K(t) with one unit. After a technology adoption at time T, an investment of one unit at time t≥T increases K(t) by q(T) units. Due to (embodied) technological progress, q(t) is increasing in t, i.e.

$$q ( 0 ) =1,\quad\quad q^{\prime} ( t ) >0\quad\text {for } t\geq0.$$

The level of q at time t denotes the productivity of the frontier technology in the economy at this time. To account for technological progress, in [8] productivity of new machines increases linearly over time, where a reference was made to Moore’s law. Analogously, we impose

$$q ( t ) =1+bt, $$

(1)

in which b is a positive constant. Alternatively, in [4] it is assumed that $q ( t ) =\operatorname {e}^{\gamma t}$, where γ is a positive constant, while in [5] there are just two technologies with different values of q available from the start.

In the absence of any adoption costs and learning effects, once the firm decides to adopt a new technology, it will always choose the technology with the highest productivity. Consequently, a technology adoption at time T implies that for t≥T the productivity of new machines of this firm equals q(T). As a result, the firm’s capital accumulation equations are

where I(t) is investment and δ is the depreciation rate. A higher level of q implies a decrease in the relative price of capital (Ref. [9] has shown that the relative price of capital has declined fairly steadily and rapidly in the post-war US and other economies) and raises the user cost of capital by the so-called obsolescence costs, cf. [10].

One motivating example for this way of modeling is the LCD industry, where our vintages correspond to generations of the production facility. With each generation the size of the mother board increases. If the mother board is larger the firm can produce in a more efficient way, so that introducing a new generation corresponds to a process innovation. For instance the fourth generation (68 by 88 cm) was first operated by LG. Philips LCD in 2000. Sharp planned to introduce the 8th generation (220 by 240 cm) in 2005. Between 2000 and 2005, several other generations became available for adoption. However, due to large sunk costs associated with building a new generation plant, and learning effects, firms typically refrain from adopting all of them immediately. Instead, for some time they stick to using their existing technologies in order to fully exploit the advantages of the learning curve.

Another area where there is a strong incentive not to use too many technologies at the same time is the airline industry. There commercial pilots typically only have the permission to fly one or two airplane models. If the airline would always buy the newest available model of Boeing, Airbus and so on, it would not have sufficient flexibility in assigning pilots to planes. Knowing this characteristic of their consumers, the big producers of airplanes offer different vintages at the same time. Furthermore, there is also a well developed secondary market, where older vintages can be bought.

In our model, older technologies are never scrapped. This is mainly done for simplicity since we believe that in a model with scrapping, similar results would occur but the model would be much more complicated and messy and would not add much to our understanding. In particular, note that due to exponential decay the old capital goods essentially die out very quickly in our model, so that the capital stocks in a model with scrapping would not be that much different than in our model.

The investment cost C(I) consists of acquisition cost (where the unit price is normalized to one) plus adjustment cost, which are assumed to be quadratic, i.e.

$$C ( I ) =I+\frac{c}{2}I^{2} $$

(2)

for some constant c>0. The firm maximizes the discounted cash flow stream over time. The cash inflow is revenue being a function of capital stock denoted by R(K), while the cash outflow is just the investment cost C(I).

To summarize, the optimization problem with one technology adoption¹ is

(3)

(4)

(5)

(6)

This implies that there is a Stage 1 problem that determines investment before the technology adoption:

(7)

and a Stage 2 problem determining investment after the technology adoption:

(8)

3 Linear Revenue Function

We start out analyzing a simple model with the aim to obtain analytical results. In this specification, revenue is proportional to the capital stock. This implies that the firm is a price taker in the output market and that the production function exhibits constant returns to scale. The revenue function is

$$R ( K ) =aK, $$

(9)

in which a is a positive constant. To guarantee that it is optimal to invest from the start, we impose that marginal revenue exceeds the initial user cost of capital, i.e.

$$a>\delta. $$

(10)

Furthermore, we assume away discounting and take the planning period to be finite. Because of the latter assumption we have to introduce a salvage value. The value of the firm at the horizon date τ equals $\frac{aK ( \tau ) }{\delta}$, which stands for the total revenue the firm can obtain by employing the capital stock K(τ) from the horizon date until infinity.

In this section we consider the case, where the firm can adopt a new technology only once. For illustration purposes, we analyze the same model, but then with two technology adoptions; see the Appendix.

3.1 A Model with One Technology Adoption

In case the firm can adopt a new technology only once, the resulting model is:

$$\max_{I,T}U ( T ) =\int_{0}^{\tau} \biggl(aK-I-\frac {c}{2}I^{2} \biggr) \, \operatorname {d}\!t+\frac{aK ( \tau ) }{\delta},$$

subject to ( 4 )–( 6 ). The analysis of the model consists of three parts. First, we consider the time interval after the new technology is adopted. Then we analyze the time interval before the technology adoption and finally the time at which the firm starts investing in the new technology is studied.

3.1.1 Stage 2: The Situation After the New Technology is Adopted

At the time interval [T,τ] the standard capital accumulation problem

arises and we can apply Pontryagin’s maximum principle; see [11]. The Hamiltonian is

$$H_{2}=aK- \biggl( I+\frac{c}{2}I^{2} \biggr) +\lambda_{2} \bigl( q ( T ) I-\delta K \bigr) ,$$

where λ _i is the co-state variable in Stage i, i=1,2. The necessary optimality conditions are:

(11)

(12)

(13)

From ( 12 ), ( 13 ) and (11) it is clear that both the co-state variable λ ₂ and the investment rate I are constant over time, i.e.

(14)

Combining this with ( 5 ), it automatically follows that

3.1.2 Stage 1: The Situation Before the New Technology is Adopted

At the time interval [0,T] we have the capital accumulation problem ( 7 ) with specification (9), leading to the Hamiltonian

$$H_{1}=aK- \biggl( I+\frac{c}{2}I^{2} \biggr) +\lambda_{1} ( I-\delta K ) ,$$

so that the necessary optimality conditions are:

(15)

(16)

From [2, 4] we know that the co-state variable is continuous at the technology adoption time T. This gives the transversality condition

$$\lambda_{1} ( T ) =\frac{a}{\delta},$$

and like in Stage 2, we derive from ( 16 ) and ( 15 ) that co-state and investment rate are constant and given by

(17)

From (14) and (17) we obtain that investment jumps up with the amount of

$$\bar{I}_{2}-\bar{I}_{1}= \bigl( q ( T ) -1 \bigr)\frac {a}{c\delta}=\frac{abT}{c\delta}>0. $$

(18)

We conclude that the adoption of a new technology implies that the firm increases investment. This is because after time T investment is more efficient, since a given amount implies a larger increase of the capital stock.

3.1.3 Determination of the Technology Adoption Time

It is straightforward to understand that adopting a new technology at time zero or at time τ gives the same objective value as not adopting a new technology at all, which is clearly not optimal. This implies that the adoption time T must be such that 0<T<τ. The following proposition provides an explicit expression for a unique value of such a T satisfying the necessary optimality conditions.

Proposition 3.1

The firm optimally adopts the new technology at time

$$T=\frac{1}{3ab} \bigl( ab\tau-2 ( a-\delta ) +\sqrt {4 ( a-\delta )^{2}+2ab\tau ( a-\delta ) +a^{2}b^{2}\tau^{2}}\bigr) . $$

(19)

The implication is that the firm invests in the less efficient technology during a longer time interval than it invests in the more efficient one, i.e.

$$0<\tau-T<\frac{\tau}{2}<T. $$

(20)

Proof

See the Appendix. □

The result ( 20 ) is surprising, since, after all, an earlier switch would enable the firm to use a more efficient technology earlier. However, by waiting longer, the firm can adopt a more productive technology. Apparently, at τ/2, the latter effect dominates the former one.

It is interesting to note that this adoption time depends on all parameters of the model except for the initial capital stock level, which is due to linearity of the revenue function. We now perform some comparative statics for the adoption time with respect to the other parameters. First, we study the dependence of T on marginal revenue a:

$$\frac{\partial T}{\partial a}=\frac{\delta}{3a^{2}b} \biggl( \frac {4 (a-\delta ) +ab\tau}{\sqrt{a^{2}b^{2}\tau^{2}+2a^{2}b\tau +4a^{2}-2ab\tau\delta-8a\delta+4\delta^{2}}}-2 \biggr) <0.$$

Hence, the more efficiently the firm produces, the earlier it adopts the new technology. The reason is that the productivity increase of a technology adoption is higher the higher a is. So when the firm waits with adopting a new technology while a is large, the opportunity cost of waiting is high.

Next, we address the effect of technological progress b:

$$\frac{\partial T}{\partial b}=\frac{ ( a-\delta )}{3ab^{2}} \biggl( 2-\frac{4 ( a-\delta ) +ab\tau}{\sqrt{a^{2}b^{2}\tau^{2}+2a^{2}b\tau+4a^{2}-2ab\tau\delta-8a\delta+4\delta^{2}}} \biggr) >0$$

So, if technological progress goes faster, it pays to wait longer with adopting a new technology. A similar result is numerically obtained in [12].

Finally, we consider the effect of the depreciation rate δ:

$$\frac{\partial T}{\partial\delta}=\frac{1}{3ab} \biggl( 2-\frac {4 (a-\delta ) +ab\tau}{\sqrt{a^{2}b^{2}\tau^{2}+2a^{2}b\tau +4a^{2}-2ab\tau\delta-8a\delta+4\delta^{2}}} \biggr) >0.$$

Hence, the firm adopts the new technology later when the depreciation rate is higher. The reason is that the net value of the investment is smaller when the depreciation rate is bigger. To make the adoption of a new technology sufficiently profitable, the firm has to adopt a better technology. To do so it employs technological progress by delaying the technology adoption time. In the Appendix, we extend this analysis by allowing for two technology adoptions and show that a similar result like Proposition 3.1 still holds.

4 Market Power

In this section we study the effect of market power, which implies that the output price is decreasing in quantity. The result is that the revenue function is concave. For our analysis we employ the following specification:

$$R(K)=aK-\frac{m}{2}K^{2}.$$

We also take into account that the firm discounts future revenue and costs. We restrict ourselves to analyzing the case of one technology adoption.

In this section, we first study the firm’s investment behavior after it has adopted the new technology. We proceed by analyzing the firm’s investments before it adopts the new technology. Finally, all the obtained information is employed to determine an implicit expression for the technology adoption time. We also provide an analytical proof for a negative anticipation effect in investment, thereby extending [8] where this effect was only numerically shown. We end this section with a numerical analysis.

4.1 The Situation After Technology Adoption (Stage 2)

The Hamiltonian for the problem after the firm has adopted the new technology, thus for t∈[T,∞[, is

$$H_{2}=aK-\frac{m}{2}K^{2}- \biggl( I+\frac{c}{2}I^{2} \biggr) +\lambda_{2} \bigl( q ( T ) I-\delta K \bigr) . $$

(21)

The necessary optimality conditions are:

(22)

(23)

Straightforward calculations lead to the following linear dynamic system:

(24)

(25)

The steady state is given by

(26)

Hence, an equilibrium with positive capital stock and investment rate exists, provided that $q ( T ) >\frac{r+\delta}{a}$. To check the stability of the interior equilibrium we compute the Jacobian of the canonical system ( 24 ), ( 25 ):

$$J=\bigg \vert \begin{array}{c@{\quad}c}-\delta& q ( T ) \\\frac{q ( T ) }{c}m & r+\delta \end{array} \bigg \vert =-\delta ( r+\delta ) -\frac{q^{2} (T ) }{c}m<0. $$

(27)

This implies that the steady state is (saddle point) stable. We end this part by stating the following lemma.

Lemma 4.1

The saddle point path in the (K,I)-plane is given by

$$I_{\mathrm{SPP2}} ( t ) =\frac{1}{\kappa}K ( t ) + \biggl( \frac{\delta}{q(T)}-\frac{1}{\kappa} \biggr) \bar{K}_{2}, $$

(28)

in which κ depends on

$$\xi_{1}=\frac{1}{2}r-\frac{1}{2}\sqrt{\frac{4m}{c} \bigl( q ( T ) \bigr)^{2}+ ( r+2\delta )^{2}}, $$

(29)

being the negative eigenvalue of the Jacobian matrix, where κ<0 is the first element of the corresponding eigenvector

$$\left ( \begin{array}{c}\kappa\\1\end{array} \right ) =\left ( \begin{array}{c}-\frac{c}{mq ( T ) } ( \delta+r-\xi_{1} ) \\1\end{array} \right ) . $$

(30)

The corresponding expressions for capital stock, investment, and co-state are

(31)

(32)

(33)

Proof

See the Appendix. □

4.2 The Situation Before Technology Adoption (Stage 1)

Similarly to the analysis of Stage 2, we find that the dynamic system is given by

Although the Stage 1 interval is of finite length, we still need to specify the steady state because it is needed to determine the optimal time path (see ( 40 ) presented below). The steady state is

(34)

Hence, an equilibrium with positive levels of the capital stock and the investment rate exists, provided that a>r+δ. To check stability, we compute the Jacobian:

$$J=\bigg \vert \begin{array}{c@{\quad}c}-\delta& 1 \\\frac{m}{c} & r+\delta \end{array} \bigg \vert =-\delta ( r+\delta ) -\frac{m}{c}<0. $$

(35)

This implies that the steady state is (saddle point) stable. The eigenvalues of the Jacobian are

(36)

(37)

and the eigenvector corresponding to the negative eigenvalue χ ₁ is

$$\left ( \begin{array}{c}\kappa_{1} \\1\end{array} \right ) =\left ( \begin{array}{c}-\frac{c}{m} ( \delta+r-\chi_{1} ) \\1\end{array} \right ) , $$

(38)

while the eigenvector with respect to the positive eigenvalue χ ₂ is

$$\left ( \begin{array}{c}\kappa_{2} \\1\end{array} \right ) =\left ( \begin{array}{c}-\frac{c}{m} ( \delta+r-\chi_{2} ) \\1\end{array} \right ) . $$

(39)

The solution is

$$\left ( \begin{array}{c}K ( t ) \\I ( t )\end{array} \right ) =\beta \left ( \begin{array}{c}\kappa_{1} \\1\end{array} \right ) \operatorname {e}^{\chi_{1}t}+\gamma \left ( \begin{array}{c}\kappa_{2} \\1\end{array} \right ) \operatorname {e}^{\chi_{2}t}+\left ( \begin{array}{c}\bar{K}_{1} \\\bar{I}_{1}\end{array} \right ) , $$

(40)

with $\bar{K}_{1}$ and $\bar{I}_{1}$ defined in ( 34 ), while β and γ will be determined in Proposition 4.2 below. The co-state variable satisfies

$$\lambda_{1} ( t ) =1+c \bigl( \beta \operatorname {e}^{\chi_{1}t}+\gamma \operatorname {e}^{\chi _{2}t}+\bar{I}_{1} \bigr) . $$

(41)

4.3 Adoption Time

We now determine the optimal adoption time T, the investment behavior, and the capital stock

$$K ( T ) =K_{T} $$

(42)

at time T. The following proposition establishes that investment jumps upwards at the adoption time. Like in the model with the linear revenue function, this is because the new technology is more productive.

Proposition 4.1

At the adoption time T, investment jumps up with the amount of

$$I \bigl( T^{+} \bigr) -I \bigl( T^{-} \bigr) = \bigl( q (T ) -1 \bigr) \biggl( I \bigl( T^{-} \bigr) +\frac{1}{c}\biggr) >0. $$

(43)

Proof

From ( 22 ), ( A.18 ) and continuity of the co-state at time T (see, e.g. [4]) it follows that

$$1+cI \bigl( T^{+} \bigr) =\lambda ( T ) q ( T ) ,\quad 1+cI \bigl(T^{-} \bigr) =\lambda ( T ) ,$$

from which ( 43 ) trivially results. □

The following proposition provides an implicit condition for the adoption time T.²

Proposition 4.2

The optimal switching time T is implicitly determined by

$$\lambda(T) \bigl( q(T)-1 \bigr) \bigl( \lambda(T) \bigl( q(T)+1 \bigr) -2 \bigr)-2bc\varOmega(K_{T},T)=0, $$

(44)

where λ(T) equals

$$\lambda ( T ) =1+c \bigl( \beta \operatorname {e}^{\chi_{1}T}+\gamma \operatorname {e}^{\chi _{2}T}+\bar{I}_{1} \bigr) , $$

(45)

in which

(46)

(47)

Furthermore,

(48)

with $\bar{K}_{1}$ and $\bar{I}_{1}$ from (34), $\bar{K}_{2}$ and $\bar{I}_{2}$ from (26), χ ₁ from (36), χ ₂ from (37), κ ₁ from (38), κ ₂ from (39), ξ ₁ from (29), and κ from (30).

Proof

See the Appendix. □

The level of the capital stock at the switching time can now be derived from (40), where β and γ satisfy the expressions presented in Proposition 4.2.

The following proposition compares the optimal trajectory with the one corresponding to the model without technology switch, i.e. where

$$\dot{K}=I-\delta K\quad\text{for } t\in ( 0,\infty ) .$$

The proposition shows that before a new technology is adopted, the firm reduces investment in the current technology.

Proposition 4.3

Adoption of a new technology at time T results in a negative anticipation effect in the sense that less investments in the current technology occur before time T compared to the saddle point path corresponding to the problem without technology switch.

Proof

See the Appendix. □

This result tells us that in fixing its investment the firm anticipates a future technology switch. Given the future rise in productivity, it becomes attractive to wait for the new technology. Cutting down on current investments reduces the capital stock, which in turn raises marginal revenue. This gives the firm the incentive to invest more in the new technology right after the technology switch. In this way, the firm accelerates substituting the new for the old technology. The analytical proof of the anticipation effect provided by Proposition 4.3 adds to [8], where this effect was derived within a vintage capital framework. We elaborate on this result in the next section.

4.4 Example

Here we provide a numerical analysis departing from the parameter values

$$a=1,\quad m=0.00008,\quad b=\frac{1}{3}\log2,\quad c=0.01,\quad r=0.1,\quad \delta=0.2.$$

The value for b is based on Moore’s law (the efficiency of a technology doubles every n years, where we put n=3), while production is a logarithmic function of the technological efficiency in the sense that production increases with one unit in case technology power becomes ten times as large.³

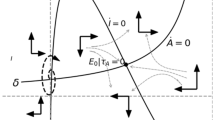
The first three panels of Fig. 1 depict the optimal trajectories in the (K,I)-plane for increasing values of K ₀. All solutions have in common the upward jump in investment at the adoption time as derived in Proposition 4.1.

Fig. 1

The optimal solution in the phase plane for different initial capital stocks: (a) K ₀=1, (b) K ₀=630, and (c) K ₀=2500. Panel (d) illustrates the dependence of the adoption time T, the capital stock at adoption time K _T , and the long-run optimal capital $\bar{K}_{2}$ on the initial capital K ₀. The other parameters are: $a=1,\ m=0.00008,\ b=\frac{1}{3}\log2,\ c=0.01,\ r=0.1,\$and δ=0.2. In addition, a movie that shows the solutions corresponding to a continuously varying initial capital stock is provided on the web page http://prolog.univie.ac.at/research/technology/movie1.avi

The first three panels also depict the optimal trajectory in case there is no possibility of a technology switch (gray curve). Then the firm converges to the steady state $\bar{E}_{1}$. We conclude that, compared to the “non-technology switch solution,” especially right before the adoption time, the firm cuts down on investment. This is a negative anticipation effect (see also [8]), which can be explained as follows. Less investment results in a downward effect on the capital stock, which, due to diminishing returns induced by the concavity of the revenue function, in turn raises marginal revenue. This makes that after the adoption of the new technology, investment becomes more profitable. Therefore, right after the adoption time investment jumps to a higher level, so that the new technology is optimally exploited. In other words, cutting down on current investment makes room for more future investments once the more efficient technology is adopted, and this accelerates replacing old technology capital stock by new technology capital stock. In the linear model of Sect. 3, marginal revenue was not affected by the capital stock level. For this reason the negative anticipation effect did not occur there. In Stage 2 capital stock gradually increases such that the trajectory asymptotically converges to the steady state $\bar{E}_{2}$.

What we also see in the first three panels of Fig. 1 is that the capital stock at the adoption time is increasing in the initial value of the capital stock, which is confirmed in panel (d). From panel (d) we can also conclude that the adoption time itself is increasing in K ₀ too. This implies that a larger firm adopts the new technology at a later point of time, which means that this new technology is more efficient due to technological progress. The smaller firm switches earlier because a small firm has a high marginal revenue, which implies that it is more profitable to adopt a more efficient technology soon. This raises the opportunity cost of waiting with adopting the new technology, and this implies that the small firm will adopt sooner. The implication is that the long-run optimal capital stock (steady state of Stage 2, $\bar{K}_{2}$) is also increasing in the initial value of the capital stock K ₀. This indeed results from the fact that the higher the initial capital stock the later the firm adopts a new technology, implying that then the new technology is more efficient. This higher efficiency leads to a higher value of $\bar{K}_{2}$.

5 Conclusions

This paper studies optimal firm growth in an innovative environment. The frontier technology in the economy improves over time due to technological progress. A firm can get access to improved capital goods by technology adoption. After such a technology adoption the relative price of capital decreases, implying that investment as well as the long-run capital goods level jumps up.

The paper starts out studying a simple dynamic model of the firm in which revenue is linear, discounting is absent and the horizon date is finite. This enables us to get analytical expressions for the optimal timing of technology adoption.

Then the paper proceeds with studying a dynamic model of the firm with an infinite time horizon, where cash flows are discounted, and the revenue function is concave. However, the firm is allowed to adopt a new technology only once. Here we could analytically prove that technology adoption induces a negative anticipation effect, i.e. before the firm adopts a new technology it cuts down on investments in the capital goods associated with the “old” technology. Since revenues are concave, these reduced investments result in higher marginal revenue just after the new technology is adopted, implying that it is optimal to raise investments in the “new” capital goods. Furthermore, numerically we showed that a large firm switches later. This has the drawback that it uses a less efficient technology for a longer time, but the advantage is that the later switch implies that the adopted new technology is more productive. This in turn implies that it will be optimal to converge to a larger long-run capital stock level. Hence, a firm that is large initially, will also be large in the long run.

As a topic of future research we have the following in mind. As it is now, in our framework the firm can costlessly adopt a new technology. However, as argued by e.g. [13], in reality firms often face major problems in integrating new technologies, which leads to switch-over disruptions. Incorporating this would enable us to endogenize the number of technology adoptions. In this way we could extend [13] by adding capital accumulation to the technology adoption analysis.

Appendix A

1.1 A.1 Proof of Proposition 3.1

Based on [2, 4] we know that at the technology adoption time T we have the following condition:

(A.1)

Inserting the expressions for H ₁(T) and H ₂(T) gives

from which we obtain after some rearranging:

$$p ( T ) =3abT^{2}+ \bigl( 4 ( a-\delta ) -2ab\tau \bigr) T-2\tau ( a-\delta ) =0.$$

Because of ( 10 ) this second-order polynomial in T has the unique positive root ( 19 ). The result ( 20 ) directly follows from the three inequalities

and the fact that the quadratic polynomial p(T) is strictly convex.

1.2 A.2 Model with Linear Revenue and Two Technology Adoptions

Now we extend for the linear model the number of technology adoption possibilities of the firm from one to two. Denoting the two adoption times by T ₁ and T ₂, the model straightforwardly becomes

Similarly to the analysis of the case with one technology adoption, it is easily obtained that

(A.2)

where, as before, λ is the co-state variable. So again, investment is constant as long as the firm invests in the same technology, while it jumps upwards after every new technology adoption.

The following proposition determines the second adoption time T ₂ as a function of the first adoption time T ₁.

Proposition A.1

Given the first adoption time T ₁, the firm optimally adopts a new technology for the second time at time T ₂ that is implicitly determined by

$$3abT_{2}^{2}+ \bigl( 4 ( a-\delta ) -2ab\tau \bigr)T_{2}- \bigl( 2 ( a-\delta ) +abT_{1} \bigr)T_{1}-2 ( a-\delta ) \tau =0, $$

(A.3)

or, in explicit form:

(A.4)

Proof

Based on [2–4] we know that at the technology adoption time T ₂ we have the following condition:

(A.5)

where H ₂ and H ₃ are the Hamiltonians at the intervals [T ₁,T ₂] and [T ₂,τ]. Their values just before and just after the second adoption time T ₂ are

The difference is

$$H_{3} ( T_{2} ) -H_{2} ( T_{2} ) =\frac {ab}{c\delta}( T_{1}-T_{2} ) -\frac{ab}{2c\delta^{2}} ( T_{1}-T_{2} ) \bigl[ 2a+ab (T_{1}+T_{2} ) \bigr] .$$

Plugging this into ( A.5 ) gives

$$\frac{ab}{c\delta} ( T_{1}-T_{2} ) -\frac{ab}{2c\delta^{2}} (T_{1}-T_{2} ) \bigl[ 2a+ab ( T_{1}+T_{2}) \bigr] =ab\frac{q ( T_{2} ) a-\delta}{c\delta^{2}} ( \tau -T_{2} ) ,$$

(A.6)

which ultimately leads to

$$3abT_{2}^{2}+ \bigl( 4 ( a-\delta ) -2ab\tau \bigr)T_{2}- \bigl( 2 ( a-\delta ) +abT_{1} \bigr)T_{1}-2\tau ( a-\delta ) =0.$$

Because of ( 10 ) this gives the unique positive root ( A.4 ). □

This adoption time depends on all parameters of the model and on the previous adoption time T ₁ except for the initial capital stock of this stage. We see that T ₂ goes up with T ₁. A larger T ₁ implies that the firm has adopted a more efficient technology at T ₁ so that it is not so much in a hurry to adopt a new technology for a second time. An analogous result is numerically obtained in [12].

Concerning the first time that the firm adopts a new technology, we can establish the following proposition.

Proposition A.2

Given the second adoption time T ₂, the firm adopts a technology optimally for the first time at T ₁, which is implicitly determined by

$$3abT_{1}^{2}+ \bigl( 4 ( a-\delta ) -2abT_{2}\bigr) T_{1}-2 ( a-\delta ) T_{2}=0, $$

(A.7)

or explicitly we can write

$$T_{1}=\frac{1}{3ab} \Bigl( abT_{2}-2 ( a-\delta ) +\sqrt {4 ( a-\delta )^{2}+2ab ( a-\delta ) T_{2}+a^{2}b^{2}T_{2}^{2}}\Bigr) . $$

(A.8)

Proof

At T ₁ it holds that

(A.9)

where H ₁ and H ₂ are the Hamiltonians in the intervals [0,T ₁] and [T ₁,T ₂]. Their values just before and just after the first adoption time T ₁ are

The difference is

$$H_{2} ( T_{1} ) -H_{1} ( T_{1} ) =\frac {ab}{2c\delta^{2}}\bigl( abT_{1}^{2}+2T_{1}( a-\delta ) \bigr) .$$

Plugging this into ( A.9 ) gives

$$\frac{ab}{2c\delta^{2}} \bigl( abT_{1}^{2}+2T_{1} (a-\delta ) \bigr) =ab\frac{ ( 1+bT_{1} ) a-\delta}{c\delta^{2}} ( T_{2}-T_{1} ) ,$$

(A.10)

which ultimately leads to

$$3abT_{1}^{2}+ \bigl( 4 ( a-\delta ) -2abT_{2}\bigr) T_{1}-2 ( a-\delta ) T_{2}=0.$$

Because of ( 10 ) this quadratic polynomial has the unique positive root ( A.8 ). □

It can be seen from ( A.4 ) and ( A.8 ) that the adoption times T ₁ and T ₂ depend on each other. To determine T ₁ and T ₂ explicitly, we first note that from (A.7) it follows that

$$T_{2}=\frac{3abT_{1}^{2}+4 ( a-\delta )T_{1}}{2abT_{1}+2 (a-\delta ) }. $$

(A.11)

Substitution of (A.11) into (A.3) eventually gives

(A.12)

In principle the relevant root of this fourth-order polynomial can be found analytically but the expression would fill too much space. Nevertheless, some general results can be obtained that are presented in the following proposition.

Proposition A.3

The optimal adoption times T ₁ and T ₂ are unique. Furthermore, the time interval at which the first technology is used is the largest,   followed by the second technology and then by the third technology, since it holds that

$$\tau-T_{2}<T_{2}-T_{1}<T_{1}, $$

(A.13)

and thus

$$T_{1}>\frac{\tau}{3}\quad\text{\textit{and}}\quad T_{2}>\frac{2\tau}{3}. $$

(A.14)

Proof

First, existence of an interior adoption time can be established. We start out by showing that the polynomial ( A.12 ) has at least one root in the relevant interval, so that T ₁∈]0,τ[. This is because at T ₁=0, the polynomial has a negative value:

$$P ( 0 ) =-8 ( a-\delta )^{3}\tau<0, $$

(A.15)

and, on the other hand, for T ₁=τ we have

$$P ( \tau ) =11a^{3}b^{3}\tau^{4}+44a^{2}b^{2}\tau^{3} ( a-\delta ) +52ab\tau^{2} ( a-\delta )^{2}+16\tau ( a-\delta )^{3}>0. $$

(A.16)

Since P(T ₁) is continuous, indeed the polynomial ( A.12 ) has at least one root in the relevant interval.

From (A.11), it follows that

$$T_{2}=2T_{1}-\frac{abT_{1}^{2}}{2abT_{1}+2 ( a-\delta ) },$$

which implies that

$$T_{2}-T_{1}<T_{1}.$$

This establishes the second part of ( A.13 ).

Now we consider the length of the time interval that the firm produces with its most efficient technology, i.e. the technology it adopts at T ₂. From (A.3) it is obtained that

$$3abT_{2}^{2}+4 ( a-\delta ) T_{2}- \bigl( 2 ( a-\delta ) +abT_{1} \bigr) T_{1}= \bigl( 2abT_{2}+2( a-\delta ) \bigr) \tau,$$

so that

$$\tau-T_{2}=\frac{ab ( T_{2}+T_{1} ) +2 ( a-\delta ) }{2abT_{2}+2 ( a-\delta ) } ( T_{2}-T_{1} )<T_{2}-T_{1},$$

which establishes the first part of ( A.13 ).

What remains to be shown is the uniqueness of the adoption times T ₁ and T ₂. Since uniqueness of T ₂ follows from eventual uniqueness of T ₁ via ( A.11 ), it suffices to show uniqueness of T ₁. We already know that P(τ)>0 from ( A.16 ). Since from ( A.14 ) it follows that $T_{1}>\frac{\tau}{3}$, it is now sufficient to show that $P ( \frac{\tau}{3} ) <0$ and P′′(T ₁)>0 for $T_{1}>\frac{\tau}{3}$. Hence, we first evaluate

$$P \biggl( \frac{\tau}{3} \biggr) =-\frac{1}{81}ab\tau^{2}\bigl( ab\tau \bigl( 84 ( a-\delta ) +13ab\tau \bigr) +108 ( a-\delta )^{2} \bigr) <0.$$

Then, we compute

Now P′′(T ₁)>0 is equivalent to

Since straightforward calculations give

$$\frac{\tau}{3}>\frac{1}{23ab} \bigl( -20 ( a-\delta ) +3ab\tau+\sqrt{3}\sqrt{26 ( a-\delta )^{2}+3ab\tau \bigl( 2 ( a-\delta ) +ab\tau \bigr) } \bigr).$$

the desired result, i.e. P′′(T ₁)>0 for $T_{1}>\frac{\tau}{3}$, directly follows from ( A.14 )). □

Again we see that like in the case where the firm can adopt a new technology only once, the optimal adoption times are such that the more productive the technology, the shorter the time interval the firm invests in the corresponding capacity.⁴

Next, we analyze the effect of the different parameters on the lengths of the time intervals at which the different technologies are used. From ( A.11 ) it follows that the difference in length between the two intervals of use of the first and second technology is

$$L=T_{1}- ( T_{2}-T_{1} ) =\frac {abT_{1}^{2}}{2abT_{1}+2 (a-\delta ) }.$$

It follows that

This gives the following result.

Proposition A.4

More difference in the lengths of the time intervals at which the firm produces with the first technology and the second technology arises when b and δ are larger, and a is smaller.

The ratio of the durations of the last two production intervals is given by

$$Le=\frac{\tau-T_{2}}{T_{2}-T_{1}}=\frac{ab ( T_{2}+T_{1} )+2 ( a-\delta ) }{2abT_{2}+2 ( a-\delta ) }.$$

It follows that

which leads to the following proposition.

Proposition A.5

The relative difference in the lengths of the time intervals, where production takes place with the second and the third technology, goes up with b and δ, while it goes down with a.

Combining this with the proposition where the first and the second production interval were compared leads to the conclusion that intervals become more of equal length when b and δ are smaller, while a is larger.

It is reasonable that the adoption times will be delayed when the planning period becomes longer. The next proposition shows that this is indeed true.

Proposition A.6

The firm adopts the second and third technology later when τ increases.

Proof

From ( A.7 ) and ( A.3 ) we obtain the total differentials:

The latter equation shows that T ₁ and T ₂ move in the same direction. This equation also gives dT ₂, which can be plugged into the first one. After some manipulations we get that

The term in front of dτ is clearly negative. To prove the first part of the proposition, we have to show that the term in front of dT ₁ is positive. For this it is sufficient that

$$4 \biggl( T_{1}+T_{2}-\frac{\tau}{2} \biggr) ( a-\delta ) -ab \bigl( T_{1}^{2}+3T_{2}^{2}+3\tau T_{1}-\tau T_{2}-9T_{1}T_{2} \bigr) >0.$$

This is implied by ( 15 ). □

1.3 A.3 Proof of Lemma 4.1

We compute the saddle-point path solution. The eigenvalues of the Jacobian are given by

$$\xi_{1,2}=\frac{1}{2}r\mp\frac{1}{2}\sqrt{\frac{4m}{c} \bigl( q ( T ) \bigr)^{2}+ ( r+2\delta )^{2}},$$

and the eigenvector corresponding to the negative eigenvalue ξ ₁ is

$$\left ( \begin{array}{c}\kappa\\1\end{array} \right ) =\left ( \begin{array}{c}-\frac{c}{mq ( T ) } ( \delta+r-\xi_{1} ) \\1\end{array} \right ) .$$

It is immediately clear that κ<0. The solution corresponding to the saddle point path is

$$\left ( \begin{array}{c}K ( t ) \\I ( t )\end{array} \right ) =\alpha \left ( \begin{array}{c}\kappa\\1\end{array} \right ) \operatorname {e}^{\xi_{1} ( t-T ) }+\left ( \begin{array}{c}\bar{K}_{2} \\\bar{I}_{2}\end{array} \right ) .$$

From the given initial value K(T) we can compute α. Equation $K ( T ) =\alpha\kappa+\bar{K}_{2}$ gives $\frac {K (T ) -\bar{K}_{2}}{\kappa}=\alpha$, i.e. we obtain ( 31 ) and ( 32 ). Then (33) can be derived by combining (32) and (22).

1.4 A.4 Proof of Proposition 4.2

The Hamiltonian for the problem before the firm has adopted the new technology, thus when t∈[0,T], is

$$H_{1}=aK-\frac{m}{2}K^{2}- \biggl( I+\frac{c}{2}I^{2} \biggr) +\lambda_{1} ( I-\delta K ) , $$

(A.17)

and the necessary optimality conditions are:

(A.18)

Based on [2, 3] a general formula connecting the two stages was developed by [4]. For our model this condition becomes

$$H_{1} ( T ) =H_{2} ( T ) -q^{\prime} ( T ) \int _{T}^{\infty} \operatorname {e}^{-r ( t-T ) }\lambda_{2} ( t )I ( t )\, \operatorname {d}\!t. $$

(A.19)

Using ( A.17 ) and ( 21 ) we obtain that

with Ω from ( 48 ).

Exploiting ( A.18 ) and ( 22 ) for I(T ⁻) and I(T ⁺), respectively, eventually gives ( 44 ). Equality ( 45 ) directly follows from ( 41 ).

Using ( 33 ) and ( 32 ) the integral in ( A.19 ) can be analytically computed yielding the closed-form solution ( 48 ).

In order to determine β and γ, we need two conditions. The first one is immediately obtained from the initial condition

$$K_{0}=K ( 0 ) =\beta\kappa_{1}+\gamma\kappa_{2}+\bar{K}_{1}.$$

(A.20)

The second one comes from the terminal condition for I(T ⁻) by combining ( 40 ) for I(T ⁻), ( 28 ) for I(T ⁺), and the jump condition ( 43 ). This ultimately leads to ( 46 ) and ( 47 ).

1.5 A.5 Proof of Proposition 4.3

The outline of the proof is as follows. Considering that the switching time is T and the switching state is K _T we show that the value of the objective function at the first stage can be improved if the initial state of the canonical system lies at or above the corresponding stable manifold of the equilibrium $E_{1}=(\bar{K}_{1},\,\bar{I}_{1})$. Therefore, we explicitly calculate the integral

$$C(\beta,\gamma):=\int_0^T\operatorname {e}^{-rt}\biggl(aK(t)-\frac {m}{2}K^2(t)-I(t)-\frac{c}{2}I^2(t)\biggr)\operatorname {d}\!t$$

along a path

This yields, after some tedious but elementary calculations:

We abbreviate this equation by collecting terms of the coefficients of β,γ, their squares, and their products:

(A.21)

Next, we prove that the coefficients of β and γ are negative. Let us start with $\varOmega_{1}(a):=a\kappa_{1}-1-\bar {K}_{1}(m\kappa_{1}+c\delta)$. First, we observe that

$$\varOmega_1(r+\delta)=(r+\delta)\kappa_1-1<0,$$

where we used that κ ₁<0. Next, we note that

Hence, Ω ₁(a) is strictly decreasing and therefore negative for all a≥r+δ. Since χ ₁<0, this results in

$$\frac{\operatorname {e}^{(\chi_1-r)T}-1}{\chi_1-r}>0.$$

We can now conclude that indeed the coefficient of β is negative.

Now we consider the coefficient of γ. First, we prove that $\varOmega_{2}(a):=a\kappa_{2}-1-\bar{K}_{1}(m\kappa_{2}+c\delta)<0$ for all a≥r+δ. To prove this proposition we consider the special case a=r+δ. From the definition of κ ₂ we derive the following inequality:

This results in

$$\varOmega_2(r+\delta)=(r+\delta)\kappa_2-1<0.$$

Next, we derive

From the above, we conclude that Ω ₂(a)<0 for all a≥r+δ. After observing that

$$\frac{\operatorname {e}^{(\chi_2-r)T}-1}{\chi_2-r}>0,$$

we indeed find that also the coefficient of γ is negative.

The coefficient of γβ is zero, which immediately follows from the definitions of κ ₁ and κ ₂.

To analyze the coefficients of the squares β ² and γ ², we consider the factors

$$\frac{\operatorname {e}^{(\chi_i-r)T}-1}{\chi_i-r}>0,\quad i=1,2$$

and note that $m\kappa_{i}^{2}+c>0,\,i=1,2$. Hence, the coefficients are positive.

Next, we prove that the objective value for a trajectory $(\tilde{K}(\cdot),\tilde{I}(\cdot))$, satisfying the canonical system on the interval [0, T] with K(T)=K _T and starting above the stable path, has a lower objective value than the stable path itself. Let $(\tilde{\beta},\tilde{\gamma})$ with $\tilde{\gamma}>0$ correspond to the path $(\tilde{K}(\cdot),\tilde{I}(\cdot))$ and (β _s ,0) denote the corresponding values for the path at the stable manifold. Note that γ _s =0 by definition of the stable path. Then we show that

$$C(\tilde{\beta},\tilde{\gamma})-C(\beta_s,0)<0.$$

To do so, we use the boundary conditions at T satisfying

yielding

$$\tilde{\beta}-\beta_s=-\tilde{\gamma}\frac{\kappa_2\operatorname {e}^{\chi _2T}}{\kappa_1\operatorname {e}^{\chi_1T}}>0,$$

since $\tilde{\gamma}>0$. Using the representation (A.21) we find

$$C(\tilde{\beta},\tilde{\gamma})-C(\beta_s,0)= (\tilde{\beta}-\beta_s )\varLambda_1-\frac{ (\tilde{\beta}-\beta_s)^2}{2}\varLambda_4+\tilde{\gamma}\varLambda_2-\frac{\tilde{\gamma}^2}{2}\varLambda_5<0,$$

which proves that the saddle path solution is superior to the solution $(\tilde{K}(\cdot),\tilde{I}(\cdot))$.

Finally, we show that the optimal solution lies beneath the saddle path solution. To do so, we prove that in a neighborhood of the saddle path the value of the objective is further increasing for a negative γ. To see this, let us consider a solution (K _h (⋅),I _h (⋅)) with corresponding values (β _h ,γ _h ) and γ _h =−hΔ<0, where h,Δ>0. Similarly to the previous case we then find

yielding

$$C(\beta_h,\gamma_h)=\beta_h\varLambda_1-\frac{\beta_h^2}{2}\varLambda_4-\gamma_h\varLambda_2-\frac{\gamma_h^2}{2}\varLambda_5+\varLambda_3.$$

Analyzing the limit

yields

We conclude that the optimal solution in Stage 1 starts beneath the stable manifold of E ₁, where the corresponding path exhibits the negative anticipation effect.