Feedback Regulation and Its Efficiency in Biochemical Networks

Abstract

Intracellular biochemical networks fluctuate dynamically due to various internal and external sources of fluctuation. Dissecting the fluctuation into biologically relevant components is important for understanding how a cell controls and harnesses noise and how information is transferred over apparently noisy intracellular networks. While substantial theoretical and experimental advancement on the decomposition of fluctuation was achieved for feedforward networks without any loop, we still lack a theoretical basis that can consistently extend such advancement to feedback networks. The main obstacle that hampers is the circulative propagation of fluctuation by feedback loops. In order to define the relevant quantity for the impact of feedback loops for fluctuation, disentanglement of the causally interlocked influences between the components is required. In addition, we also lack an approach that enables us to infer non-perturbatively the influence of the feedback to fluctuation in the same way as the dual reporter system does in the feedforward networks. In this work, we address these problems by extending the work on the fluctuation decomposition and the dual reporter system. For a single-loop feedback network with two components, we define feedback loop gain as the feedback efficiency that is consistent with the fluctuation decomposition for feedforward networks. Then, we clarify the relation of the feedback efficiency with the fluctuation propagation in an open-looped FF network. Finally, by extending the dual reporter system, we propose a conjugate feedback and feedforward system for estimating the feedback efficiency non-perturbatively only from the statistics of the system.

1 Introduction

1.1 Dissecting Fluctuation in Biochemical Networks

Biochemical molecules in a cell fluctuate dynamically because of the stochastic nature of intracellular reactions, fluctuation of the environment, and the spontaneous dynamics of intracellular networks [18, 33, 41]. Some part of the fluctuation is noise that impairs or disturbs robust operation of the intracellular networks. The other part, however, conveys information on complex dynamics of various factors inside and outside of the cell [20, 32]. Dissecting fluctuation into distinct components with different biological roles and meanings is crucial for understanding the mechanisms how a cell controls and harnesses the noise and how information is transferred over apparently noisy intracellular networks [5, 9].

The intracellular fluctuation is generated from the intracellular reactions or comes from the environment, and then propagates within the intracellular networks. The fluctuation of individual molecular species within the networks is therefore a consequence of the propagated fluctuation from the different sources. Decomposition of the fluctuation into the contributions from the sources is an indispensable step for understanding their biological roles and relevance. When fluctuation propagates from one component to another unidirectionally without circulation, the fluctuation of the downstream can be decomposed into two contributions. One is the intrinsic part that originates within the pathway between the components. The other is the extrinsic part that propagates from the upstream component. Such decomposition can easily be extended for the network with cascading or branching structures in which no feedback exists. This fact drove the intensive anatomical analysis of the intracellular fluctuation.

1.2 Decomposition of Sources of Fluctuation

In order to dissect fluctuation into different components, two major strategies have been developed. One is to use the dependency of each component on different kinetic parameters of the network. By employing theoretical predictions on such dependency, we can estimate the relative contributions of different components from single-cell experiments with perturbations. Possible decompositions of the fluctuation were investigated theoretically for various networks such as single gene expression [3, 27, 28], signal transduction pathways [42, 48], and cascading reactions [46]. Some of them were experimentally tested [3, 27, 29].

The other strategy is the dual reporter system in which we simultaneously measure a target molecule with its replica obtained by synthetically duplicating the target. From the statistics of the target and the replica, i.e, mean, variance, and covariance, we can discriminate the intrinsic and extrinsic contributions to the fluctuation because the former is independent between the target and the replica whereas the latter is common to them. The idea of this strategy was proposed and developed in [28, 44], and verified experimentally for different organisms [11, 24, 34]. Its applicability and generality were further extended [4, 6, 16, 17, 36]. Now these strategies play the fundamental role for designing single-cell experiments and for deriving information on the anatomy of fluctuation from experimental observations [8, 15, 30, 35, 38, 45].

1.3 Feedback Regulation and Its Efficiency

Even with the theoretical and the experimental advancement in decomposing fluctuation, most of works focused on the feedforward (FF) networks in which no feedback and circulation exists. As commonly known in the control theory [7, 40], feedback (FB) loops substantially affect fluctuation of a network by either suppressing or amplifying it. Actually, the suppression of fluctuation in a single gene expression with a FB loop was experimentally tested in [2] earlier than the decomposition of fluctuation. While the qualitative and the quantitative impacts of the FB loops were investigated both theoretically and experimentally since then [1, 22, 25, 26, 36, 43, 47], we still lack a theoretical basis that can consistently integrate such knowledge with that on the fluctuation decomposition developed for FF networks.

The main problem that hampers the integration is the circulation of fluctuation in FB networks. Because fluctuation generated at a molecular component propagates the network back to itself, we need to disentangle the causally interlocked influence between the components in order to define the relevant quantity for the impact of the FB loops. From the experimental point of view, in addition, quantification of the impact of FB loops by perturbative experiments is not perfectly reliable because artificial blocking of the FB loops inevitably accompanies the change not only in fluctuation but also in the average level of the molecular components involved in the loops. It is quite demanding and almost impossible for most cases to inhibit the loops by keeping the average level unchanged. We still lack an approach that enables us to infer the influence of the FB non-perturbatively as the dual reporter system does for FF networks.

1.4 Outline of this Work

In this work, we address these problems by extending the work on the fluctuation decomposition [28, 42] and the dual reporter system [11, 44]. By using a single-loop FB network with two components and its linear noise approximation (LNA) [10, 19, 47], we firstly provide a definition of the FB loop gain as FB efficiency that is consistent with the fluctuation decomposition in [28, 42]. This extension relies on an interpretation of the fluctuation decomposition as source-by-source decomposition that is different from the variance decomposition proposed in the previous work [4, 6, 16, 17]. Then, we clarify the relation of the FB efficiency with the fluctuation propagation in a corresponding open-looped FF network. Finally, by extending the dual reporter system, we propose a conjugate FB and FF system for estimating the feedback efficiency only from the statistics of the system non-perturbatively. We also give a fluctuation relation among the statistics that may be used to check the validity of the LNA for a given network.

The rest of this paper is organized as follows. In Sect. 2, we review the decomposition of fluctuation for a simple FF system derived in [28, 42] by using the LNA. In Sect. 3, we extend the result shown in Sect. 2 to a FB network by deriving a source-by source decomposition of the fluctuation with feedback. Using this source decomposition, we define the FB loop gains that quantify the impacts of the FB to the fluctuation. In Sect. 4, we give a quantitative relation of the loop gains in the FB network with the fluctuation propagation in a corresponding open-looped FF network. In Sect. 5, we propose a conjugate FF and FB network as a natural extension of the dual reporter system. We clarify that the loop gains can be estimated only from the statistics, i.e., mean, variances, and covariances, of the conjugate network. We also show that a fluctuation relation holds among the statistics, which generalizes the relation used in the dual reporter system. In Sect. 6, we discuss a link of the conjugate network with the casual conditioning and the directed information, and finally give future directions of our work.

2 Fluctuation Decomposition and Propagation in a Small Biochemical Network

In this section, we summarize the result for the decomposition of fluctuation obtained in [28, 42] by using the LNA, and also its relation with the dual reporter system employed in [11, 24, 34] to quantify the intrinsic and extrinsic contributions from the experimental measurements.

2.1 Stochastic Chemical Reaction and Its Linear Noise Approximation

Let us consider a chemical reaction network consisting of N different molecular species and M different reactions. We assume that the stochastic dynamics of the network is modeled by the following chemical master equation:

$$\begin{aligned} \frac{\mathrm {d}\mathbb {P}(t,\varvec{n})}{\mathrm {d}t}=\sum _{k=1}^{M}\left[ a_{k}(\varvec{n}-\varvec{s}_{k})\mathbb {P}(t,\varvec{n}-\varvec{s}_{k})- a_{k}(\varvec{n})\mathbb {P}(t,\varvec{n})\right] , \end{aligned}$$

(1)

where $\varvec{n}=(n_{1}, \ldots , n_{N})^{\mathbb {T}}\in \mathbb {N}_{\ge 0}^{N}$ is the numbers of the molecular species, $\mathbb {P}(t,\varvec{n})$ is the probability that the number of molecular species is $\varvec{n}$ at t, and $a_{k}(\varvec{n}) \in \mathbb {R}_{\ge 0}^{M}$ and $\varvec{s}_{k}\in \mathbb {N}^{N}$ are the propensity function and the stoichiometric vector of the kth reaction, respectively [12, 14, 19]. The propensity function, $a_{k}$, characterizes the probability of occurrence of the kth reaction when the number of the molecular species is $\varvec{n}$, and the stoichiometric vector defines the change in the number of the molecular species when the kth reaction occurs.

In general, it is almost impossible to directly solve Eq. (1) both analytically and numerically because it is a high-dimensional or infinite-dimensional differential equation. To obtain insights for the dynamics of the reaction network, several approximations have been introduced [12, 19]. Among others, the first-order approximation is the deterministic reaction equation that is described for the given propensity functions and the stoichiometric vector as

$$\begin{aligned} \frac{\mathrm {d}\Omega \varvec{u}(t)}{\mathrm {d}t} = S \varvec{a}(\Omega \varvec{u(t)}), \end{aligned}$$

(2)

where $\Omega$ is the system size, $\varvec{u}\in \mathbb {R}_{\ge 0}^{n}$ is the concentration of $\varvec{n}$ as $\varvec{u}=\varvec{n}/\Omega$, $\varvec{a}(\varvec{n}):\,=(a_{1}(\varvec{n)}), \ldots , a_{M}(\varvec{n}))^{\mathbb {T}}$, and $S:\,=(\varvec{s}_{1}, \ldots , \varvec{s}_{M})$ is the stoichiometric matrix. Equation (2) was successfully applied for chemical reaction networks with large system size where the fluctuation of the concentration of the molecular species can be neglected. When the system size is not sufficiently large, however, Eq. (2) is not appropriate for analyzing dynamics and fluctuation of the network. The LNA is a kind of the second-order approximation of the Eq. (1) that characterizes the fluctuation around a fixed point, $\bar{\varvec{n}}$, of Eq. (2) that satisfies $S \varvec{a}(\varvec{\bar{n}})=0$. The stationary fluctuation of the network around $\bar{\varvec{n}}$ is then obtained by solving the following Lyapunov equation [10, 19, 47]

$$\begin{aligned} (K(\bar{\varvec{n}})\varvec{\Sigma })+(K(\bar{\varvec{n}})\varvec{\Sigma })^{\mathbb {T}}+D(\bar{\varvec{n}})=0, \end{aligned}$$

(3)

where

$$\begin{aligned} K_{*,j}(\varvec{n}):\,=\frac{\partial S\varvec{a}(\varvec{n})}{\partial n_{j}},\qquad D_{i,j}(\varvec{n}):\,=\sum _{k} s_{i,k}s_{j,k}a_{k}(\varvec{n}), \end{aligned}$$

(4)

and $\varvec{\Sigma }$ is the covariance matrix of $\varvec{n}$. When the propensity function $\varvec{a}(\varvec{n})$ is affine with respect to $\varvec{n}$, the dynamics of $\Omega \varvec{u}(t)$ determined by Eq. (2) is identical to that of the first cumulant of n, i.e., the average of n, as

$$\begin{aligned} \frac{\mathrm {d}\left<\varvec{n}\right>}{\mathrm {d}t} = S \varvec{a}(\left<\varvec{n}\right>), \end{aligned}$$

(5)

where $\left<\varvec{n}\right> :\,=\sum _{\varvec{n}}\varvec{n}\mathbb {P}(t,\varvec{n})$. In addition, the second cumulant, i.e., the covariance matrix, follows the Lyapunov equation as

$$\begin{aligned} \frac{\mathrm {d} \varvec{\Sigma }}{\mathrm {d}t}=(K(\left<\varvec{n}\right> )\varvec{\Sigma })+(K(\left<\varvec{n}\right> )\varvec{\Sigma })^{\mathbb {T}}+D(\left<\varvec{n}\right> ). \end{aligned}$$

(6)

Therefore, if the propensity function $\varvec{a}(\varvec{n})$ is affine, the stationary fluctuation of $\varvec{n}$ is exactly described by Eq. (3). For a non-affine $\varvec{a}(\varvec{n})$, Eqs. (5) and (6) can also be regarded as an approximation of the full cumulant equations by the cumulant closure [12] under which we ignore the influence of the second and the higher order cumulants to Eq. (5), and that of the third and the higher order ones to Eq. (6).¹ Even though the propensity function $\varvec{a}(\varvec{n})$ is not affine, Eq. (3) (or Eq. (6)) can produce a good approximation of the fluctuation, provided that the fixed point, $\bar{\varvec{n}}$, is a good approximation of the average, $\left<\varvec{n} \right>$, and that the local dynamics around the fixed point is approximated enough by its linearization. In addition, compared with other approximations, the LNA enables us to obtain an analytic representation of the fluctuation because Eq. (3) is a linear algebraic equation with respect to $\varvec{\Sigma }$. Owing to this property, the LNA and its variations played the crucial role to reveal the analytic representation of the fluctuation decomposition in biochemical reaction networks [21, 28, 47]. As in these previous works, we employ the LNA to obtain an analytic representation for the feedback efficiency.

2.2 Decomposition of Fluctuation

Starting from the LNA, Paulsson derived an analytic result on how noise is determined in a FF network with two components (Fig. 1a) [28]. Here, we briefly summarize the result derived in [28]. Let $n_{1}=x$ and $n_{2}=y$ for notational simplicity, and consider the FF reaction network (Fig. 1a) with the following propensity function and stoichiometric matrix,

$$\begin{aligned} \varvec{a}(x,y)=(a_{x}^{+}(x),a_{x}^{-}(x),a_{y}^{+}(x,y),a_{y}^{-}(x,y))^{T},\qquad S=\begin{pmatrix} +1 &{} -1 &{} 0 &{} 0 \\ 0 &{} 0 &{} +1 &{} -1 \end{pmatrix}. \end{aligned}$$

(7)

Because $a_{x}^{\pm }$ depends only on x, x regulates y unidirectionally. Then, for a fixed point $(\bar{x},\bar{y})$ of Eq. (2), that satisfies

$$\begin{aligned} a_{x}^{+}(\bar{x}) =a_{x}^{-}(\bar{x}), \quad a_{y}^{+}(\bar{x},\bar{y})=a_{y}^{-}(\bar{x},\bar{y}), \end{aligned}$$

(8)

K and D in Eq. (3) becomes

$$\begin{aligned} K&=\begin{pmatrix} -d_{x} &{} 0\\ k_{yx}&{} -d_{y} \end{pmatrix}= \begin{pmatrix} -H_{xx}/\tau _{x} &{} 0\\ -\frac{\bar{y}}{\bar{x}}H_{yx}/\tau _{y}&{} -H_{yy}/\tau _{y} \end{pmatrix}, \quad D=\begin{pmatrix} 2 \bar{a}_{x} &{} 0 \\ 0 &{} 2 \bar{a}_{y} \end{pmatrix}, \end{aligned}$$

(9)

where $\bar{a}_{x} :\,=a_{x}^{+}(\bar{x}) =a_{x}^{-}(\bar{x})$, $\bar{a}_{y}=a_{y}^{+}(\bar{x},\bar{y})=a_{y}^{-}(\bar{x},\bar{y})$, and $H_{i,j}:\,=\left. \frac{\partial \ln a_{i}^{-}/a_{i}^{+}}{\partial \ln j}\right| _{(\bar{x},\bar{y})}$ for $i,j \in \{x,y\}$. $\tau _{x}:\,=\bar{x}/\bar{a}_{x}$ and $\tau _{y}:\,=\bar{y}/\bar{a}_{y}$ are the effective life-time of x and y, respectively. $d_{x}$ and $d_{y}$ are the minus of the diagonal terms of K and represent the effective degradation rates of x and y. $k_{yx}$ is the off-diagonal term of K that represents the interaction from x to y. $H_{ij}$ is the susceptibility of the ith component to the perturbation of the jth one. Except this section, we mainly use ds and ks as the representation of the parameters rather than Hs and $\tau$s introduced in [28].² By solving Eq. (3) analytically, the following fluctuation-dissipation relation was derived in [28]:

$$\begin{aligned} \frac{\sigma _{x}^{2}}{\bar{x}^{2}}=\underbrace{\frac{1}{\bar{x} H_{xx}}}_{(I)},\quad \frac{\sigma _{y}^{2}}{\bar{y}^{2}}=\underbrace{\frac{1}{\bar{y} H_{yy}}}_{(II)} + \underbrace{\overbrace{\left( \frac{H_{yx}/\tau _{y}}{H_{yy}/\tau _{y}}\right) ^{2}}^{(iii)}\overbrace{\frac{H_{yy}/\tau _{y}}{H_{yy}/\tau _{y}+H_{xx}/\tau _{x}}}^{(ii)}\overbrace{\frac{\sigma _{x}^{2}}{\bar{x}^{2}}}^{(i)}}_{(III)}. \end{aligned}$$

(10)

This representation measures the intensity of the fluctuation by the coefficient of variation (CV),³ and describes how the fluctuation generates and propagates within the network. (I) is the intrinsic fluctuation of x that originates from the stochastic birth and death of x. $1/\bar{x}$ reflects the Poissonian nature of the stochastic birth and death, and $1/H_{xx}$ is the effect of auto-regulatory FB. Similarly, (II) is the intrinsic fluctuation of y that originates from the stochastic birth and death of y. (III), on the other hand, accounts for the extrinsic contributions to the fluctuation of y due to the fluctuation of x. The term (III) is further decomposed into (i), (ii), and (iii). (i) is the fluctuation of x, and therefore, identical to (I). (ii) and (iii) determine the efficiency of the propagation of the fluctuation from x to y, which are the time-averaging and sensitivity of the pathway from x to y, respectively. This representation captures the important difference of the intrinsic and the extrinsic fluctation such that the intrinsic one, the term (II), can be always reduced by increasing the average of $\bar{y}$ whereas the extrinsic one, the term (III), cannot.⁴

Fig. 1

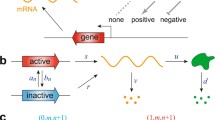
a The structure of the two-component FF network. Interpretations of this network as single-gene expression [11, 23, 27, 28], two-gene regulation [47], and signal transduction [48] are shown. b The structure of the dual reporter system [4, 11, 17, 28, 44]. c A schematic diagram of the FF network for two-gene regulation. d A schematic diagram of the dual reporter network for the two-gene regulation

While Eq. (10) provides an useful interpretation on how the fluctuation propagates in the FF network, it is not appropriate for the extension to the FB network because the contribution of x to the fluctuation of y is described by the CV of x as the term (i). Because the fluctuation of x and y depend mutually if we have a FB between x and y, we need to characterize the fluctuation of y without directly using the fluctuation of x. To this end, we adopt the variances and covariances as the measure of the fluctuation and use the following decomposition of the fluctuation for the FF network:

$$\begin{aligned} \sigma _{x}^{2}=\underbrace{\overbrace{G_{x,x}}^{(ii)}\overbrace{\bar{x}}^{(i)}}_{(I)},\qquad \sigma _{y}^{2}=\underbrace{\overbrace{G_{yy}}^{(ii)}\overbrace{\bar{y}}^{(i)}}_{(II)} + \underbrace{\overbrace{G_{yx}}^{(iii)}\overbrace{G_{x,x}}^{(ii)}\overbrace{\bar{x}}^{(i)}}_{(III)}, \end{aligned}$$

(11)

where we define $G_{xx}$, $G_{yy}$, and $G_{yx}$ as

$$\begin{aligned} G_{xx} :\,=\frac{1}{H_{xx}},\quad G_{yy} :\,=\frac{1}{H_{yy}}, \quad G_{yx} :\,=\frac{k_{yx}^{2}}{(d_{x}+d_{y})d_{y}}. \end{aligned}$$

(12)

The terms (I), (II), and (III) in Eq. (11) correspond to those in Eq. (10). The interpretation of the terms within (I), (II), and (III) is, however, different. In Eq. (11), the terms (i) are interpreted as the fluctuation purely generated by the birth and death reactions of x and y by neglecting any contribution of the auto-FBs. Because the simple birth and death of a molecular species without any regulation follow the Poissonian statistics, the intensity of the fluctuation is equal to the means of the species. Thus, $\bar{x}\approx \left<x\right>$ and $\bar{y}\approx \left<y\right>$ in the terms (i) represent the generation of the fluctuation by the birth and death of x and y, respectively. The fluctuation generated is then amplified or suppressed by the auto-regulatory FBs. $G_{xx}$ and $G_{yy}$ in the terms (ii) account for this influence, and are denoted as auto-FB gains in this work. Finally, $G_{yx}$ in the term (iii) quantifies the efficiency of the propagation of the fluctuation from x to y. We denote $G_{yx}$ as path gain from x to y. If we use the notation in Eq. (10), $G_{yx}$ is described as

$$\begin{aligned} G_{yx}= \left( \frac{\bar{y}H_{yx}/\tau _{y}}{\bar{x}H_{yy}/\tau _{y}}\right) ^{2}\frac{H_{yy}/\tau _{y}}{H_{yy}/\tau _{y}+H_{xx}/\tau _{x}}. \end{aligned}$$

(13)

The decomposition of the fluctuation of y into (II) and (III) is consistent between Eqs. (10) and (11) while the further decompositions within (II) and (III) are different.

We can systematically obtain the decomposition into (II) and (III) as in Eq. (11) by solving the Lyapunov equation, Eq. (3), with $\bar{a}_{x}$ and $\bar{a}_{y}$ being replaced with 0, respectively. Because $\bar{a}_{x}$ and $\bar{a}_{y}$ represent the noise sources associated with each variable, we call our decomposition as source-by-source decomposition or more simply as source decomposition [47].⁵ At the same time, it was also revealed in [4, 6, 16, 17] that the decomposition into (II) and (III) is identical to the variance decomposition formula in statistics as

$$\begin{aligned} \sigma _{y}^{2}&= \mathbb {V}_{y}[y(t)]= \underbrace{\mathbb {E}_{\mathcal {X}}[\mathbb {V}_{y}[y(t)|\mathcal {X}(t)]]}_{(II)} +\underbrace{\mathbb {V}_{\mathcal {X}}[\mathbb {E}_{y}[y(t)|\mathcal {X}(t)]]}_{(III)} , \end{aligned}$$

(14)

where $\mathcal {X}(t):\,=\{x(\tau );\tau \in [0,t]\}$ is the history of x(t), and $\mathbb {E}$ and $\mathbb {V}$ are the expectation and the variance, respectively.⁶ While the source decomposition and the variance decomposition are different in general, they coincide in this special case of the simple FF network. Because the variance decomposition formula holds generally even for a non-stationary situation without using the linearization by the Lyapunov equation, the variance decomposition, Eq. (14), has wider applicability than the source decomposition, Eqs. (10) and (11), as a decomposition formula.⁷ Nonetheless, the source decomposition has advantages as a decomposition formula when we extend the decompositions to FB networks as discussed in the next section.

2.3 Dual Reporter System

The decomposition, Eqs. (10) or (11), guides us how to evaluate the intrinsic and the extrinsic fluctuation in y experimentally. When we can externally control the mean of y without affecting the term (III), we can estimate the relative contributions of (II) and (III) as the intrinsic and the extrinsic fluctuation by plotting $\sigma _{y}^{2}$ as a function of the mean of y. When x and y correspond to mRNA and protein in the single gene expression, the translation rate works as such a control parameter [23]. This approach was intensively employed to estimate the efficiency of the fluctuation propagation in various intracellular networks [3, 27, 29].

Another way to quantify the intrinsic and the extrinsic fluctuation is the dual reporter system adopted in [11, 24, 34] whose network structure is shown in Fig. 1b.⁸ In the dual reporter system, a replica of y is attached to the downstream of x as in Fig. 1b where $y'$ denotes the molecular species of the replica. The replica $y'$ must have the same kinetics as y, and must be measured simultaneously with y. If y is a protein whose expression is regulated by another protein x as in Fig. 1c, then $y'$ can be synthetically constructed by duplicating the gene of y and attaching fluorescent probes with different colors to y and $y'$ as in Fig. 1d [11]. Under the LNA, the covariance between y and $y'$ can be described as

$$\begin{aligned} \sigma _{y,y'}=G_{yx}G_{xx}\bar{x}. \end{aligned}$$

(15)

Thus, by using only the statistics of the dual reporter system, the intrinsic and the extrinsic components in y can be estimated as

$$\begin{aligned} \sigma _{y}^{2}=\underbrace{G_{yy}\bar{y}}_{(II)} + \underbrace{\sigma _{y, y'}}_{(III)}, \end{aligned}$$

(16)

where it is unnecessary to control any kinetic parameters externally. In the variance decomposition (Eq. (14)), the term (III) is $\mathbb {V}[\mathbb {E}[y(t)|\mathcal {X}(t)]]$. As shown in [4], this correspondence between $\mathbb {V}[\mathbb {E}[y(t)|\mathcal {X}(t)]]$ and $\sigma _{y,y'}$ for the dual reporter system is more generally derived as

$$\begin{aligned} \sigma _{y, y'}&= \mathbb {E}[y(t)y'(t)]-\mathbb {E}[y(t)]\mathbb {E}[y'(t)], \nonumber \\&=\mathbb {E}[\mathbb {E}[y(t)y'(t)|\mathcal {X}(t)]]-\mathbb {E}[\mathbb {E}[y(t)|\mathcal {X}(t)]]\mathbb {E}[\mathbb {E}[y'(t)|\mathcal {X}(t)]], \nonumber \\&=\mathbb {E}[\mathbb {E}[y(t)|\mathcal {X}(t)]\mathbb {E}[y'(t)|\mathcal {X}(t)]]-\mathbb {E}[\mathbb {E}[y(t)|\mathcal {X}(t)]]\mathbb {E}[\mathbb {E}[y'(t)|\mathcal {X}(t)]],\\&=\mathbb {V}[\mathbb {E}[y(t)|\mathcal {X}(t)]],\nonumber \end{aligned}$$

(17)

where we used $\mathbb {E}[y(t)]=\mathbb {E}[y'(t)]$ and $\mathbb {E}[y(t)y'(t)|\mathcal {X}(t)]=\mathbb {E}[y(t)|\mathcal {X}(t)]\mathbb {E}[y'(t)|\mathcal {X}(t)]$ if y(t) and $y'(t)$ are conditionally independent given the history, $\mathcal {X}(t)$. As discussed in [4], the term (II) is also directly estimated by calculating $\mathbb {E}[d_{\bot }^{2}]:\,=\frac{1}{2}\mathbb {E}[(y(t)-y'(t))^{2}]$ because

$$\begin{aligned} \mathbb {E}[d_{\bot }^{2}]&:\,=\frac{1}{2}\mathbb {E}[(y(t)-y'(t))^{2}]=\frac{\sigma _{y}^{2}+\sigma _{y'}^{2}}{2}- \sigma _{y(t),y'(t)} =\sigma _{y}^{2}-\sigma _{y(t),y'(t)} \nonumber \\&= G_{yy}\bar{y}, \end{aligned}$$

(18)

where we used $\sigma _{y}^{2}=\sigma _{y'}^{2}$. The dual reporter system and general variance decomposition were investigated more intensively in [4, 6, 16].

3 Feedback Loop Gain in a Small Biochemical Network

While we had substantial progress in the decomposition of the fluctuation and its experimental measurement for the FF networks in the last decade, its extension to FB networks is yet to be achieved. In this section, we extend the source decomposition of the fluctuation for the simple FF network (Eq. (11)) to the corresponding FB network depicted in Fig. 2a . As in Eq. (9), K and D in the Lyapunov equation (Eq. (3)) for the FB network can be described as

$$\begin{aligned} K=\begin{pmatrix} -d_{x} &{} k_{xy} \\ k_{yx} &{} -d_{y} \end{pmatrix} =\begin{pmatrix} -H_{xx}/\tau _{x} &{} -\frac{\bar{x}}{\bar{y}}H_{xy}/\tau _{x}\\ -\frac{\bar{y}}{\bar{x}}H_{yx}/\tau _{y}&{} -H_{yy}/\tau _{y} \end{pmatrix} ,\qquad D=\begin{pmatrix} 2 \bar{a}_{x} &{} 0 \\ 0 &{} 2 \bar{a}_{y} \end{pmatrix}. \end{aligned}$$

(19)

By defining the path gain from y back to x as

$$\begin{aligned} G_{xy}:\,=\frac{k_{xy}^{2}}{d_{x}(d_{x}+d_{y})}, \end{aligned}$$

(20)

we can derive the source decomposition of the fluctuation of x and y as

$$\begin{aligned} \sigma _{x}^{2}&=\frac{1-L_{y}}{1-L_{x}-L_{y}}\overbrace{G_{xx}\bar{x}}^{(I)} \,+\, \frac{1}{1-L_{x}-L_{y}}\overbrace{G_{xy}G_{yy}\bar{y}}^{(IV)}, \nonumber \\ \sigma _{y}^{2}&=\frac{1-L_{x}}{1-L_{x}-L_{y}}\underbrace{G_{yy}\bar{y}}_{(II)} \,+\, \frac{1}{1-L_{x}-L_{y}}\underbrace{G_{yx}G_{xx}\bar{x}}_{(III)}, \end{aligned}$$

(21)

where we define

$$\begin{aligned} L_{x}:\,=\frac{k_{xy}k_{yx}}{d_{x}(d_{x}+d_{y})},\qquad L_{y}:\,=\frac{k_{xy}k_{yx}}{(d_{x}+d_{y})d_{y}}. \end{aligned}$$

(22)

If the FB from y to x does not exist, i.e., $k_{xy}=0$, then $L_{x}=L_{y}=G_{xy}=0$ and Eq. (21) is reduced to Eq. (11). Thus, $L_{x}$ and $L_{y}$ account for the effect of the FB. $L_{x}$ and $L_{y}$ are denoted as FB loop gains in this work. Eq. (21) clearly demonstrates that the representation in Eq. (10) does not work with the FB because $\sigma _{y}^{2}$ cannot be described with $\sigma _{x}^{2}$ any longer. In contrast, we can interpret the terms in Eq. (21) consistently with those in Eq. (11) because all the terms, (I), (II) and (III), are unchanged in Eq. (21). The new term, (IV), in the expression for $\sigma _{x}^{2}$ appears to account for the propagation of the fluctuation generated by the birth and death events of y back to x.⁹

Equations (21) and (22) indicate how the FB affects the fluctuation of x and y. First, the fluctuation is suppressed when $L_{x}$ and $L_{y}$ are negative whereas it is amplified when they are positive. When $d_{x}$ and $d_{y}$ are positive,¹⁰ the sign of $L_{x}$ and $L_{y}$ are determined only by the sign of $k_{xy}k_{yx}$. Thus, the FB loop is negative when x regulates y positively and y does x negatively or vise versa. This is consistent with the normal definition of the sign of a FB loop. Second, the efficiency of the FB depends on the source of the fluctuation. For example, when $L_{x}\ll L_{y}$, e.g., the time-scale of x is much faster than y as $d_{x} \gg d_{y}$, then Eq. (21) can be approximated as

$$\begin{aligned} \sigma _{x}^{2}&=\overbrace{G_{xx}\bar{x}}^{(I)}\, +\, \frac{1}{1-L_{y}}\overbrace{G_{xy}G_{yy}\bar{y}}^{(IV)},\quad \sigma _{y}^{2}=\frac{1}{1-L_{y}}\left[ \underbrace{G_{yy}\bar{y}}_{(II)} \,+\, \underbrace{G_{yx}G_{xx}\bar{x}}_{(III)}\right] . \end{aligned}$$

Thus, the FB does not work on the term (I) that is the part of fluctuation of x whose origin is the birth and death events of x itself. This result reflects the fact that the slow FB from x to itself via y cannot affect the fast component of the fluctuation of x.¹¹ Finally, when $L_{x}$ and $L_{y}$ satisfy $1-L_{x}-L_{y}=1-k_{xy}k_{yx}/d_{x}d_{y}=0$, the fluctuation of both x and y diverges due to the FB. Since this condition means that the determinant of K becomes 0 and K is the Jacobian matrix of Eq. (2), the fluctuation of x and y diverges due to the destabilization of the fixed point, $\bar{\varvec{n}}$, by the FB. The Lyapunov equation is no longer valid around an unstable fixed point, and thereby, the source decomposition cannot be applied to such a situation.¹²

Fig. 2

a The structure of the two-component FB network. b A schematic diagram of the FB network for two-gene regulation

In contrast to the FF network, the source decomposition for the FB network differs from the variance decomposition because $\mathbb {E}[\mathbb {V}[y(t)|\mathcal {X}(t)]]$ in Eq. (14) is obtained for the stationary state as

$$\begin{aligned} \mathbb {E}[\mathbb {V}[y(t)|\mathcal {X}(t)]]=2 \frac{d_{x}d_{y}}{k_{xy}^{2}}\left[ -1 + \sqrt{1 + \frac{k_{xy}^{2}}{d_{x}d_{y}}\frac{G_{yy}\bar{y}}{G_{xx}\bar{x}}} \right] G_{xx}\bar{x} \le G_{yy}\bar{y}. \end{aligned}$$

(23)

The derivation is shown in Appendix 3, and $\mathbb {E}[\mathbb {V}[y(t)|\mathcal {X}(t)]]$ is reduced to $\mathbb {E}[\mathbb {V}[y(t)|\mathcal {X}(t)]]=G_{yy}\bar{y}$ as in the term (II) of Eq. (11) when there is no feedback from y to x as $k_{xy}=0$.¹³ While the variance decomposition is defined quite generally, it may not reflect the way how the fluctuation of the target is determined in the system. This fact is demonstrated clearly by noting that $\mathbb {E}[\mathbb {V}[y(t)|\mathcal {X}(t)]]$ is independent of $k_{yx}$. Even without feedback from x to y as $k_{yx}=0$, the variance of y(t) can be decomposed into two terms via the history of $\mathcal {X}(t)$ because we can infer the behavior of y(t) from the history of $\mathcal {X}(t)$ by reversing the causal relation from x(t) to y(t) by Bayes’ theorem. Because the causal relation is reversed by Bayes’ theorem, the interpretation of each decomposed component by the variance decomposition does not reflect the regulatory relation between x(t) and y(t). This property of the variance decomposition by history should be noted for its application to FB networks. In contrast, even for the FB network, the source decomposition can provide a consistent decomposition that reflects the way how the fluctuation is determined by regulatory relations within the system. We should emphasize, however, that the source decomposition requires the stationarity and the linearization of the system by the Lyapunov equation that are not necessary for the variance decomposition.¹⁴

4 Relation Between Fluctuation Propagation and Feedback Gain

As shown in Sect. 3, $L_{x}$ and $L_{y}$ are quantitatively related to the efficiency of the FB. Because $L_{x}L_{y}=G_{xy}G_{yx}$ holds, the loop gains are also linked to the propagation of the fluctuation from x to y and from y back to x. However, the meaning of the individual gains, $L_{x}$ and $L_{y}$, is still ambiguous.

Fig. 3

a The structure of the the opened FF network obtained by replicating y in the FB network. b A schematic diagram of the network in a for gene regulation. c The structure of the the opened FF network obtained by replicating x in the FB network. d A schematic diagram of the network in c for gene regulation

To clarify the relation between the loop gains and the propagation of fluctuation, we consider a three-component FF network shown in Fig. 3a, b that are obtained by opening the FB network in Fig. 2a. In the network shown in Fig. 3a, x is regulated not by y but by its replica, $y'$. We assume that $y'$ is not driven by x and that y does not drive x. Thereby, $y' \rightarrow x \rightarrow y$ forms a FF network. K and D in Eq. (3) for this network become

$$\begin{aligned} K=\begin{pmatrix} -d_{y'} &{} 0 &{} 0 \\ k_{xy'} &{} -d_{x} &{} 0 \\ 0 &{} k_{yx} &{} - d_{y} \end{pmatrix},\qquad D=\mathrm {diag}\begin{pmatrix} 2 \bar{a}_{y'}&2 \bar{a}_{x}&2 \bar{a}_{y} \end{pmatrix}. \end{aligned}$$

(24)

Because $y'$ is the replica of y, we assume that all the kinetic parameters of $y'$ are equal to those of y as $k_{xy'}=k_{xy}$, $d_{y'}=d_{y}$, and $\bar{a}_{y'}=\bar{a}_{y}$.

By solving Eq. (3), we can obtain the following decomposition of the fluctuation of y as

$$\begin{aligned} \sigma _{x}^{2}&=\overbrace{G_{xx}\bar{x}}^{(I)} \,+\, \overbrace{G_{xy'}G_{y'y'}\bar{y}'}^{(IV)},\nonumber \\ \sigma _{y}^{2}&=\underbrace{G_{yy}\bar{y}}_{(II)} \,+\, \underbrace{G_{yx}G_{xx}\bar{x}}_{(III)} + \underbrace{\left[ G_{yy'}+G_{yxy'}\right] G_{y'y'}\bar{y}'}_{(V)}, \end{aligned}$$

(25)

where

$$\begin{aligned} G_{xy'}=G_{xy},\quad G_{yxy'}&:\,=G_{yx}G_{xy'}=G_{yx}G_{xy}=L_{x}L_{y},\quad G_{yy'}:\,=L_{y}^{2}/2. \end{aligned}$$

(26)

This decomposition of $\sigma _{y}^{2}$ can also be related to the generalized variance decomposition [4] as

$$\begin{aligned} \sigma _{y}^{2}&=\underbrace{\mathbb {E}[\mathbb {V}[y(t)|\{\mathcal {X}(t),\mathcal {Y}'(t)\}]]}_{(II)} + \underbrace{\mathbb {E}[\mathbb {V}[\mathbb {E}[y(t)|\{\mathcal {X}(t),\mathcal {Y}'(t)\}]|\mathcal {Y}'(t)]]}_{(III)} + \underbrace{\mathbb {V}[\mathbb {E}[y(t)|\mathcal {Y}'(t)]]}_{(V)}. \end{aligned}$$

(27)

The derivation is shown in Appendix 5. The term (IV) for x is similar to the propagation of the fluctuation from y to x in the FB network, but it represents the propagation of the fluctuation from the replica $y'$ in this opened FF network. The new term (V) accounts for the propagation of the fluctuation from $y'$ down to y. The gain of this propagation has two terms, $G_{yxy'}$ and $G_{yy'}$. The first term, $G_{yxy'}$, is the total gain of the propagation from $y'$ to x and from x to $y'$ because $G_{yxy'}=G_{yx}G_{xy'}$ holds. In order to see the meaning of the term $G_{yy'}$, we need to rearrange Eq. (25) as

$$\begin{aligned} \sigma _{y}^{2}&=G_{yy}\bar{y} + G_{yx}\sigma _{x}^{2} + G_{yy'}G_{y'y'}\bar{y}'. \end{aligned}$$

(28)

This representation clarifies that $G_{yy'}$ describes the propagation of the fluctuation from $y'$ to y that cannot be reflected to the fluctuation of the intermediate component, x. In addition, by solving Eq. (3), we can see that the gain $G_{yy'}$ is directly related to the covariance between y and $y'$ as

$$\begin{aligned} \sigma _{y',y}=\sqrt{G_{yy'}}\bar{y'}=\frac{L_{y}}{2}\bar{y'}. \end{aligned}$$

(29)

This implies that we have at least two types of propagation of the fluctuation. One described by $G_{yxy'}$ is that the fluctuation of the upstream, i.e., $y'$, is absorbed by the intermediate component, i.e., x, and then the absorbed fluctuation propagates to the downstream, i.e., y. This component does not convey the information of the upstream because that does not affect the covariance between the upstream and the downstream. The other type described by $G_{yy'}$ is that the fluctuation of the upstream propagates to the downstream without affecting the intermediate component. This fluctuation conveys the information on the upstream to the downstream because it is directly linked to their covariance. The fact that $L_{y}$ is related to the latter indicates that the FB efficiency is directly linked to the information transfer in the opened loop from $y'$ to y. By considering another opened loop network where the replica of x is introduced as in Fig. 3c, we can obtain the following result:

$$\begin{aligned} \sigma _{y}^{2}&=\overbrace{G_{yy}\bar{y}}^{(II)} + \overbrace{G_{yx'}G_{x'x'}\bar{x}'}^{(III)}, \nonumber \\ \sigma _{x}^{2}&=\underbrace{G_{xx}\bar{x}}_{(I)} + \underbrace{G_{xy}G_{yy}\bar{y}}_{(IV)} + \underbrace{\left[ G_{xx'}+G_{xyx'}\right] G_{x'x'}\bar{x}'}_{(VI)}, \end{aligned}$$

(30)

where $G_{xx'}:\,=L_{x}^{2}/2$, and we also have

$$\begin{aligned} \sigma _{x',x}&=\sqrt{G_{xx'}}\bar{x'}=\frac{L_{x}}{2}\bar{x'}. \end{aligned}$$

(31)

By combining Eqs. (29) and (31), we can estimate the loop gains, $L_{x}$ and $L_{y}$, by only measuring the averages and covariances of the opened networks as follows:

$$\begin{aligned} \frac{L_{x}}{2}=\frac{\sigma _{x',x}}{\bar{x}'},\quad \frac{L_{y}}{2}=\frac{\sigma _{y',y}}{\bar{y}'}. \end{aligned}$$

(32)

While this strategy sounds eligible theoretically, it accompanies an experimental difficulty in constructing the opened networks. In the opened network, the replica, e.g., $y'$, must be designed so that it is free from the regulation of x by keeping all the other properties and kinetic parameters the same as those of y. For example, if x and y are regulatory proteins and if they regulate each other as transcription factors as in Fig. 2b, the replica, $y'$, must not be regulated by x but its expression rate must be equal to the average expression rate of y under the regulation of x as in Fig. 3b. This requires fine-tuning of the expression rate of $y'$ by modifying the DNA sequences relevant for the rate. In order to conduct this tuning, we have to measure several kinetic parameters of the original FB networks that undermines the advantage of the opened network such that measurements of the kinetic parameters are unnecessary to estimate $L_{x}$ and $L_{y}$ via Eq. (32).

5 Estimation of Feedback Loop Gain by a Conjugate FB and FF Network

As a more promising strategy for the measurement of the loop gains, we propose a conjugate FB and FF network that is an extension of the dual reporter system for the estimation of the intrinsic and the extrinsic components. In the conjugate network, we couple the original FB network with a replica that is opened as in Fig. 4a. x and y are the same as the original FB network. The replica, $y'$, is regulated by x as y is but does not regulate x back. Thus, x and the replica $y'$ form an FF network. If x and y are regulatory proteins as in Fig. 2b, the replica $y'$ can be engineered by duplicating the gene y with its promoter site, and by modifying the coding region of the replica so that $y'$ looses the affinity for binding to the regulatory region of x as in Fig. 4b. This modification is much easier than that required for designing the opened network in Fig. 3.

Fig. 4

a The structure of the conjugate FB and FF network obtained by replicating y in the FB network. b A schematic diagram of the network in a for gene regulation. c The structure of the conjugate FB and FF network obtained by replicating x in the FB network. d A schematic diagram of the network in c for gene regulation

Next, we show how to use this conjugate network to measure the loop gains. For this network, K and D in Eq. (3) become

$$\begin{aligned} K&=\begin{pmatrix} -d_{x} &{} k_{xy} &{} 0 \\ k_{yx} &{} -d_{y} &{} 0\\ k_{y'x} &{} 0 &{} -d_{y'} \end{pmatrix},\qquad D=\begin{pmatrix} 2 \bar{a}_{x} &{} 0 &{}0\\ 0 &{} 2 \bar{a}_{y} &{}0 \\ 0 &{}0&{} 2 \bar{a}_{y'} \end{pmatrix}. \end{aligned}$$

(33)

Because the replica $y'$ affects neither x nor y, the fluctuation of x and that of y are the same as those of the FB network in Eq. (21). The variance of the replica $y'$ can be decomposed as

$$\begin{aligned} \sigma _{y'}^{2}=\,&\overbrace{G_{y'y'}\bar{y}'}^{(II)} + \frac{(1-L_{y})+(1+L_{y'})}{(1-L_{x}-L_{y})(1-L_{y'})}\overbrace{G_{y'x}G_{xx}\bar{x}}^{(III)} \nonumber \\&+ \frac{1}{(1-L_{x}-L_{y})(1-L_{y'})}\underbrace{(G_{y'y}+G_{y'xy})G_{yy}\bar{y}}_{(V)}, \end{aligned}$$

(34)

where

$$\begin{aligned} L_{y'}=\frac{L_{y}}{2}, \quad G_{y'y'}=G_{yy},\quad G_{y'x}=G_{yx},\quad G_{y'y}=G_{yy'},\quad G_{y'xy}=G_{yx}G_{xy}. \end{aligned}$$

(35)

Rearranging this equation leads to

$$\begin{aligned} \sigma _{y'}^{2}&=\sigma _{y}^{2}-\frac{L_{y}}{1-L_{y}/2}G_{yy}\bar{y}. \end{aligned}$$

(36)

In addition, we have the following expression for the covariance between y and $y'$ as

$$\begin{aligned} \sigma _{y,y'}&=\frac{1}{(1-L_{x}-L_{y})}G_{yx}G_{xx}\bar{x}+\frac{(1+L_{x})L_{y'}}{(1-L_{x}-L_{y})(1-L_{y'})}G_{yy}\bar{y},\nonumber \\&=\sigma _{y}^{2}-\frac{1}{1-L_{y}/2}G_{yy}\bar{y}. \end{aligned}$$

(37)

A similar result can be obtained by replicating x as in Fig. 4c, d.

By using these relations, we have

$$\begin{aligned} L_{x}&=\overbrace{\frac{\sigma _{x'}^{2}-\sigma _{x}^{2}}{\sigma _{x,x'}-\sigma _{x}^{2}}}^{(a)}=\overbrace{\frac{1}{1/2+G_{xx}/(F_{x}-F_{x'})}}^{(b)}=\overbrace{2\left( 1-\frac{G_{xx}}{F_{x}-F_{x,x'}}\right) }^{(c)}, \nonumber \\ L_{y}&=\underbrace{\frac{\sigma _{y'}^{2}-\sigma _{y}^{2}}{\sigma _{y,y'}-\sigma _{y}^{2}}}_{(a)}=\underbrace{\frac{1}{1/2+G_{yy}/(F_{y}-F_{y'})}}_{(b)}=\underbrace{2\left( 1-\frac{G_{yy}}{F_{y}-F_{y,y'}}\right) }_{(c)}, \end{aligned}$$

(38)

where $F_{x}:\,=\sigma _{x}^{2}/\left<x\right>$, $F_{y}:\,=\sigma _{y}^{2}/\left<y\right>$, $F_{x,x'}:\,=\sigma _{x,x'}/\left<x\right>$, and $F_{y,y'}:\,=\sigma _{y,y'}/\left<y\right>$ are the Fano factors of x and y and normalized covariances. This result indicates that we have multiple ways, (a), (b), and (c), to estimate $L_{x}$ and $L_{y}$ from the statistics of the conjugate network. In addition, we also have a fluctuation relation that holds between the statistics as

$$\begin{aligned} F_{x}+F_{x'}-2 F_{x,x'}=2G_{xx},\qquad F_{y}+F_{y'}-2 F_{y,y'}=2G_{yy}, \end{aligned}$$

(39)

which is the generalization of Eq. (16) for the dual reporter system. Because $\bar{x}\left( F_{y}+F_{y'}-2\right. \left. F_{y,y'}\right) =\sigma _{y}^{2}+\sigma _{y'}^{2}-2 \sigma _{y,y'}=\mathbb {E}[(y(t)-y'(t))^{2}]$, we also obtain

$$\begin{aligned} \mathbb {E}[d_{\bot }^{2}] :\,=\frac{1}{2}\mathbb {E}[(y(t)-y'(t))^{2}]=G_{yy}\bar{y}. \end{aligned}$$

(40)

Note that this result is the same as Eq. (18) for the dual reporter system even though a FB exists in the conjugate FB and FF system.

Fig. 5

a A schematic diagram of the conjugate FB and FF network used for the numerical simulation. b The distributions of p(x, y) , $p(x,y')$, and $p(x',y)$ sampled from the simulation for different parameter values of $K_{x}$. The other parameters are $f_{0}=g_{0}=400$, $K_{y}=100$, and $d_{x}=d_{y}=1$. The blue, red, and green dots are the distributions of p(x, y) , $p(x,y')$, and $p(x',y)$, respectively. Solid and dashed lines are the nullclines of Eq. (2) defined as $\mathrm {d}x/\mathrm {d}t=0$ and $\mathrm {d}y/\mathrm {d}t=0$ . c The distributions of $p(y,y')$ sampled from the simulation for different parameter values of $K_{x}$. The other parameters are the same as in b. The black dashing line is $y'=y$. d $(L_{x}, L_{y})$ estimated with the relations, a, b, and c, in Eq. (38) from the numerical simulation. The parameter values used were the same as in b. For each estimation, the means and the covariances required in Eq. (38) were calculated from $9 \times 10^{4}$ samplings. For each parameter value, we calculated the estimates ten times to see their variation. Black markers show the analytically obtained values of $(L_{x}, L_{y})$ for each parameter value. e A plot of the estimates of $F_{x}+F_{x'}-2 F_{x,x'}$ and $F_{y}+F_{y'}-2 F_{y,y'}$ derived in Eq. (39). The parameter values used were the same as those in d (Color figure online)

5.1 Verification of the Relations by Numerical Simulation

We verify Eqs. (38) and (39) by using numerical simulation. For the simulation, we use a conjugate network of gene regulation in which the replicas of both x and y are involved to measure $L_{x}$ and $L_{y}$, simultaneously as in Fig. 5a. For the variable $\varvec{n}=(x,y,x',y')^{\mathbb {T}}$, the stoichiometric matrix and the propensity function are

$$\begin{aligned} S= \begin{pmatrix} 1 &{} -1 &{} 0 &{} 0 &{} 0 &{} 0 &{}0 &{}0\\ 0 &{} 0 &{} 1 &{} -1 &{} 0 &{} 0 &{}0 &{}0\\ 0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -1 &{}0 &{}0 \\ 0&{}0 &{}0 &{} 0 &{} 0 &{} 0 &{} 1 &{} -1 \end{pmatrix},\quad a(\varvec{x})= \begin{pmatrix} f(y) \\ -d_{x} x \\ g(x) \\ -d_{y} y \\ f(y) \\ -d_{x} x' \\ g(x) \\ -d_{y} y' \end{pmatrix}. \end{aligned}$$

(41)

The simulation is conducted by the Gillespie’s next reaction algorithm [13]. First, we test a linear negative feedback regulation defined by $f(y):\,=\max \left[ f_{0}[1-\frac{y}{K_{y}}], 0\right]$, and $g(x):\,=\max \left[ g_{0}\frac{x}{K_{x}}, 0\right]$ under which the LNA holds exactly as long as its trajectory has sufficiently small probability to reach the boundaries of $x=0$ and $y=0$. In Fig. 5b, the distributions of p(x, y), $p(x,y')$, and $p(x',y)$ are plotted for different parameter values of $K_{x}$. The FB is strong for small $K_{x}$ whereas it is weak for large $K_{x}$. $(L_{x}, L_{y})$ estimated by Eq. (38) for the parameter values are plotted in Fig. 5d. The three estimators, (a), (b), and (c) in Eq. (38), are used for comparison. For this simulation, all the estimators work well, but they have slightly larger variability in $L_{x}$ compared with that in $L_{y}$ for large values of $|L_{x}|$ and $|L_{y}|$. In addition, when $|L_{x}|$ and $|L_{y}|$ are very small, i.e. much less than 1, the estimators show relatively larger variability and bias, suggesting that the estimation of very weak FB efficiency requires more sampling. For the same parameter values, we also test Eq. (39) in Fig. 5e. Both $F_{x}+F_{x'}-2 F_{x,x'}$ and $F_{y}+F_{y'}-2 F_{y,y'}$ localize near 2 irrespective of the parameter values. As Figs. 5d, e demonstrate, the estimators obtained from the simulations agree with the analytical values of $(L_{x}, L_{y})$, and the fluctuation relation also holds very robustly.

Fig. 6

a The distributions of p(x, y) , $p(x,y')$, and $p(x',y)$ sampled from the simulation for different parameter values of $n_{x}$ and $n_{y}$ where $n_{x}=n_{y}=|n|$. The other parameters are $f_{0}=g_{0}=300$, $K_{x}=K_{y}=150$, and $d_{x}=d_{y}=1$. The blue, red, and green dots are the distributions of p(x, y) , $p(x,y')$, and $p(x',y)$, respectively. Solid and dashed curves are the nullclines of Eq. (2) defined as $\mathrm {d}x/\mathrm {d}t=0$ and $\mathrm {d}y/\mathrm {d}t=0$. b $(L_{x}, L_{y})$ estimated with the relations, a, b, and c, in Eq. (38) from the numerical simulation. The same parameter values were used as in a. For each estimation, the means and the covariances required in Eq. (38) were calculated from $9 \times 10^{4}$ samplings. For each parameter value, we calculated the estimates ten times to see their variation. Black markers show the analytically obtained values of $(L_{x}, L_{y})$ for each parameter value. c A plot of the estimates of $F_{x}+F_{x'}-2 F_{x,x'}$ and $F_{y}+F_{y'}-2 F_{y,y'}$ shown in Eq. (39). The parameter values used were the same as those in b (Color figure online)

In order to test how nonlinearity affects the estimation, we also investigated a non-linear negative feedback regulation defined by $f(y):\,=f_{0} \frac{1}{1+(y/K_{y})^{n_{y}}}$, and $g(x):\,=g_{0} \frac{(x/K_{x})^{n_{x}}}{1+(x/K_{x})^{n_{x}}}$. We change the Hill coefficients, $n_{x}$ and $n_{y}$, by keeping the fixed point unchanged as in Fig. 6a. Compared with the linear case, the variability of the estimators is almost similar even though the feedback regulation is nonlinear (Fig. 6b). In addition, the estimators show a good agreement with the analytical value except for very large value of $|L_{x}|$ and $|L_{y}|$. This suggests that Eq. (38) works as good estimators when the trajectories of the system are localized sufficiently near the fixed point as in Fig. 6a. For the very large value of $|L_{x}|$ and $|L_{y}|$ where $|n|=2^{7/2}$, all the estimators are slightly biased towards smaller values, and the estimator (b) in Eq. (38) has larger variance than the others. In addition, similarly to the linear case, the estimators require larger sampling when $|L_{x}|$ and $|L_{y}|$ are much less than 1. Even with the nonlinear regulation, the fluctuation relation holds robustly as shown in Fig. 6c, which is consistent with the good agreement of the estimators of $L_{x}$ and $L_{y}$ with their analytical values as in Fig. 6b.

All these results indicate that the estimators obtained in Eq. (38) can be used to estimate the FB efficiency as long as the efficiency is moderate and the trajectories of the system are localized near the fixed point.

6 Discussion

In this work, we extended the fluctuation decomposition obtained for FF networks to FB networks. In this extension, the FB loop gains are naturally derived as the measure to quantify the efficiency of the FB. By considering the opened FF network obtained by opening the loop of the FB network, the relation between the loop gains and the fluctuation propagation in the FF network was clarified. In addition, we proposed the conjugate FB and FF network as a methodology to quantify the loop gains by showing that the loop gains are estimated only from the statistics of the conjugate network. By using numerical simulation, we demonstrated that the loop gains can actually be estimated by the conjugate network while we need more investigation on the bias and variance of the estimators. Furthermore, the fluctuation relation that holds in the conjugate network was also verified. We think that our work gives a theoretical basis for the conjugate network as a scheme for experimental estimation of the FB loop gains.

The conjugate network is much easier to apply for estimating FB efficiency than perturbative approach. The procedures to measure the FB efficiency is summarized as follows. For a FB network with two components, x and y,

• 1. duplicate them to obtain their replicas, $x'$ and $y'$, by genetic engineering as in Fig. 5a;

• 2. modify the replicas, $x'$ and $y'$, so that they cannot regulate back y and x, respectively;

• 3. measure the expression levels of x and $x'$ or y and $y'$ simultaneously by single-cell measurements;¹⁵

• 4. calculate the variances and covariances of x, $x'$, y, and $y'$ from the data;

• 5. estimate the loop gains by using their estimators, (a), (b), and (c) in Eq. (38);

• 6. calculate the fluctuation relation, Eq. (39), in order to check the validity of the source decomposition.

This procedure may be applied to a network with more than two components whose slow dynamics is well characterized by two components among them. It is an open problem to extend the conjugate FB and FF network for more than two components.

As for such extension of the efficiency of FB and its quantification by the conjugate network, the generality of the source decomposition and the FB loop gain should be clarified. In the case of the FF network, the fluctuation decomposition proposed initially by using the LNA was successfully generalized as the variance decomposition formula with respect to the conditioning of the history of the upstream fluctuation [4, 17]. In the case of the FB network, similarly, the source decomposition and the FB loop gains were obtained and defined via the LNA that requires stationarity and linearization of the network. However, its generalization for non-stationary and nonlinear situation is not straightforward because of the circulative flow of the fluctuation. As we demonstrated, the variance decomposition also cannot provide appropriate information on the FB efficiency. The problem is that the normal conditioning by history in the variance decomposition does not account for the causal relation between the components. The previous work on the relation between the fluctuation decomposition and the information transfer for the FF network [4] suggests that the information-theoretic investigation may provides a clue to generalize the FB loop gains. As a candidate for such information measure, we illustrate a connection of the conjugate FB and FF network with the directed information and Kramer’s causal conditioning. Let us consider the joint probability of the histories of x(t) and y(t), $\mathbb {P}[\mathcal {X}(t),\mathcal {Y}(t)]$. From the definition of the conditional probability, we can decompose this joint probability as

$$\begin{aligned} \mathbb {P}[\mathcal {X}(t),\mathcal {Y}(t)]=\mathbb {P}[\mathcal {X}(t)|\mathcal {Y}(t)]\mathbb {P}[\mathcal {Y}(t)]=\mathbb {P}[\mathcal {Y}(t)|\mathcal {X}(t)]\mathbb {P}[\mathcal {X}(t)]. \end{aligned}$$

(42)

However, when x(t) and y(t) are causally interacting, we can decompose the joint probability differently as

$$\begin{aligned} \mathbb {P}[\mathcal {X}(t),\mathcal {Y}(t)]&=\left[ \prod _{i=1}^{t}\mathbb {P}[x_{i}|\mathcal {X}_{i-1},\mathcal {Y}_{i-1}]\right] \left[ \prod _{i=1}^{t}\mathbb {P}[y_{i}|\mathcal {X}_{i},\mathcal {Y}_{i-1}]\right] \end{aligned}$$

(43)

$$\begin{aligned}&= \mathbb {P}_{y||x}[\mathcal {Y}(t)||\mathcal {X}(t)]\times \mathbb {P}_{x||y}[\mathcal {X}(t)||\mathcal {Y}(t-1)], \end{aligned}$$

(44)

where $\mathbb {P}_{y||x}[\mathcal {Y}(t)||\mathcal {X}(t)]$ and $\mathbb {P}_{x||y}[\mathcal {X}(t)||\mathcal {Y}(t-1)]$ are the Kramer’s causal conditional probabilities [31]. If no FB exists from y back to x, then this decomposition is reduced to

$$\begin{aligned} \mathbb {P}[\mathcal {X}(t),\mathcal {Y}(t)]&= \mathbb {P}_{y||x}[\mathcal {Y}(t)||\mathcal {X}(t)]\times \mathbb {P}[\mathcal {X}(t)]. \end{aligned}$$

(45)

The directed information from y to x is defined as

$$\begin{aligned} \mathbb {I}[\mathcal {Y}(t)\rightarrow \mathcal {X}(t)] :\,=\left<\ln \frac{\mathbb {P}[\mathcal {X}(t), \mathcal {Y}(t)]}{\mathbb {P}_{y||x}[\mathcal {Y}(t)||\mathcal {X}(t)]\mathbb {P}[\mathcal {X}(t)]}\right>_{\mathbb {P}[\mathcal {X}(t), \mathcal {Y}(t)]}, \end{aligned}$$

(46)

where the joint probability of $\mathcal {X}(t)$ and $\mathcal {Y}$(t) is compared with the distribution, $\mathbb {P}_{y||x}[\mathcal {Y}(t)||\mathcal {X}(t)]\times \mathbb {P}[\mathcal {X}(t)]$ [31]. Thus, $\mathbb {I}[\mathcal {Y}(t)\rightarrow \mathcal {X}(t)]$ is zero when no FB exists from y to x, and measures the directional flow of information from y back to x. In the conjugate network, the replica $y'$ is driven only by x. Thus, the joint probability between $\mathcal {X}(t)$ and $\mathcal {Y}'(t)$ becomes

$$\begin{aligned} \mathbb {P}[\mathcal {X}(t),\mathcal {Y}'(t)]=\mathbb {P}_{y||x}[\mathcal {Y}'(t)||\mathcal {X}(t)]\mathbb {P}[\mathcal {X}(t)]. \end{aligned}$$

(47)

Thereby, in principle¹⁶ the directed information can be calculated by obtaining the joint distributions, $\mathbb {P}[\mathcal {X}(t),\mathcal {Y}(t)]$ and $\mathbb {P}[\mathcal {X}(t),\mathcal {Y}'(t)]$, of the conjugate network. This relation of the conjugate network with the directed information strongly suggests that the directed information and the causal decomposition are related to the loop gains. Resolving this problem will lead to more fundamental understanding of the FB in biochemical networks because the directed information is found fundamental in various problems such as the information transmission with FB [49], gambling with causal side information [31], population dynamics with environmental sensing [37], and the information thermodynamics with FB [39]. This problem will be addressed in our future work.

Appendices

Appendix 1: Variance and Source Decompositions as the Spacial Cases of the Orthogonal Decomposition

Th variance decomposition is known as a version of orthogonal decomposition of random variables. For two random variables, $U_{1}$ and $U_{2}$, if $U_{1}$ and $U_{2}$ are orthogonal as $\mathbb {COV}[U_{1}U_{2}]=0$, then $\mathbb {V}[U_{1}+U_{2}]=\mathbb {V}[U_{1}]+\mathbb {V}[U_{2}]$ holds. For any two random variables, $Z_{1}$ and $Z_{2}$, we can decompose $Z_{1}$ as $Z_{1}-\mathbb {E}[Z_{1}]=(\mathbb {E}[Z_{1}|Z_{2}]-\mathbb {E}[Z_{1}]) + (Z_{1}-\mathbb {E}[Z_{1}|Z_{2}])$. Because $\mathbb {E}[(\mathbb {E}[Z_{1}|Z_{2}]-\mathbb {E}[Z_{1}])]=0$, $\mathbb {E}[(Z_{1}-\mathbb {E}[Z_{1}|Z_{2}])]=0$, and $\mathbb {E}[(\mathbb {E}[Z_{1}|Z_{2}]-\mathbb {E}[Z_{1}])(Z_{1}-\mathbb {E}[Z_{1}|Z_{2}])]=0$, we have $\mathbb {V}[Z_{1}-\mathbb {E}[Z_{1}]]=\mathbb {V}[\mathbb {E}[Z_{1}|Z_{2}]-\mathbb {E}[Z_{1}]] + \mathbb {V}[Z_{1}-\mathbb {E}[Z_{1}|Z_{2}])]$. By choosing $Z_{1}=y(t)$ and $Z_{2}=\mathcal {X}(t)$, we obtain the variance decomposition as Eq. (14).

The source decomposition can also be regarded as a kind of orthogonal decomposition. Let us assume for simplicity that $D(\bar{\mathbf {n}})$ is diagonal such that each reaction induces fluctuation onto only one molecular specie.¹⁷ The variances $\Sigma$ obtained as the stationary solution of the Lyapunov equation Eq. (3) can be identified with the variances of the stationary solution of the following linear stochastic differential equations:

$$\begin{aligned} \mathrm {d}\xi _{i}(t)&= \sum _{j}K_{ij}(\bar{\mathbf {n}}) \xi _{j}\mathrm {d}t+\sqrt{D(\bar{\mathbf {n}})_{ii}}\mathrm {d}W_{i}(t),\qquad i\in \{1,\dots , N \} \end{aligned}$$

(48)

where $W_{i}(t)$ and $W_{j}(t)$ are independent white Gaussian processes for $i\ne j$. Because of the linearity of the equation, $\xi _{i}(t)$ can be decomposed as $\xi _{i}(t)=\xi _{i,1}(t)+\cdots + \xi _{i,N}(t)$ where $\xi _{i,h}(t)$ are defined as

$$\begin{aligned} \mathrm {d}\xi _{i,h}(t)&= \sum _{j}K_{ij}(\bar{\mathbf {n}}) \xi _{j,h}\mathrm {d}t+\delta _{i,h}\sqrt{D(\bar{\mathbf {n}})_{ii}}\mathrm {d}W_{i}(t),\qquad i\in \{1,\dots , N \} , \end{aligned}$$

(49)

where $\delta _{i,h}$ is the Kronecker delta. Because $\xi _{*,h}(t) :\,=\{\xi _{1,h}(t), \dots , \xi _{N,h}(t) \}^{\mathbb {T}}$ is driven only by $W_{h}(t)$, $\xi _{i,h}(t)$ accounts for the fluctuation of the ith component due to the fluctuation originating from the stochastic birth and death reactions of the hth component. Because $K(\bar{\mathbf {n}})$ is not diagonal for most applications, the effect of noise $W_{h}(t)$ injected only to the hth component of $\xi _{*,h}(t)$ propagates to the other components. Thus, $\xi _{i,h}$ is stochastic in general for all i. Because $W_{h}(t)$ and $W_{h'}(t)$ are independent for $h \ne h'$, $\xi _{i,h}(t)$ and $\xi _{i,h'}(t)$ are also mutually independent and orthogonal as $\mathbb {COV}[\xi _{i,h}(t), \xi _{i,h'}(t)]=0$. Thus, the variance of $\xi _{i}$ can be decomposed as $\mathbb {V}[\xi _{i}(t)]=\sum _{h}\mathbb {V}[\xi _{i,h}(t)]$. In addition, by definition, $\xi _{i,h}(t)$ can be described as $\xi _{i,h}(t)=\mathbb {E}[\xi _{i}(t)|\mathcal {W}_{h}(t)]$ where $\mathcal {W}_{h}(t)$ is the histories of $W_{h}(t)$. Thus, we have a representation of the source decomposition as

$$\begin{aligned} \mathbb {V}[\xi _{i}(t)]=\sum _{h}\mathbb {V}[\mathbb {E}[\xi _{i}(t)|\mathcal {W}_{h}(t)], \end{aligned}$$

(50)

where the variance of $\xi _{i}$ is decomposed into the contributions from different noise sources.¹⁸ As clearly shown, the source decomposition strongly relies on the linearity of the Lyapunov equation. Its extension to nonlinear situation is still an open problem.

Appendix 2: Source Decomposition of a FB Network with Three Components

We consider a FB network with three components, x, y, and z that forms a loop $x \rightarrow y \rightarrow z \rightarrow x$. For this FB network, K and D in the Lyapunov equation (Eq. (3)) can be described as

$$\begin{aligned} K&=\begin{pmatrix} -d_{x} &{} 0 &{} k_{xz} \\ k_{yx} &{} -d_{y} &{} 0\\ 0 &{} k_{zy} &{} -d_{z} \\ \end{pmatrix} =\begin{pmatrix} -H_{xx}/\tau _{x} &{} 0 &{} -\frac{\bar{x}}{\bar{z}}H_{xz}/\tau _{z}\\ -\frac{\bar{y}}{\bar{x}}H_{yx}/\tau _{y}&{} -H_{yy}/\tau _{y} &{} 0\\ 0&{} -\frac{\bar{z}}{\bar{y}}H_{zy}/\tau _{z}&{} -H_{zz}/\tau _{z} \\ \end{pmatrix},\end{aligned}$$

(51)

$$\begin{aligned} D&=\begin{pmatrix} 2 \bar{a}_{x} &{} 0 &{} 0 \\ 0 &{} 2 \bar{a}_{y} &{} 0 \\ 0 &{} 0 &{} 2 \bar{a}_{z} \end{pmatrix}. \end{aligned}$$

(52)

We can obtain the following source decomposition for the variance of z:

$$\begin{aligned} \sigma _{z}^{2}&=\frac{1-L_{x}-L_{y}-L_{xyz}}{1-L_{x}-L_{y}-L_{z}-L_{xyz}-L_{mix}}G_{zz}\bar{z},\end{aligned}$$

(53)

$$\begin{aligned}&\quad + \frac{1-L_{x}}{1-L_{x}-L_{y}-L_{z}-L_{xyz}-L_{mix}} G_{zy}G_{yy}\bar{y}\end{aligned}$$

(54)

$$\begin{aligned}&\quad + \frac{1}{1-L_{x}-L_{y}-L_{z}-L_{xyz}-L_{mix}}[G_{z-x}+G_{zyx}]G_{xx}\bar{x} \end{aligned}$$

(55)

where we define the path gains as

$$\begin{aligned} G_{xx}&:\,=1/H_{xx},&G_{yy}&:\,=1/H_{yy},&G_{zz}&:\,=1/H_{zz}\\ G_{yx}&:\,=\frac{k_{yx}^{2}}{d_{y}(d_{x}+d_{y})},&G_{zy}&:\,=\frac{k_{zy}^{2}}{d_{z}(d_{y}+d_{z})},&G_{xz}&:\,=\frac{k_{xz}^{2}}{d_{x}(d_{x}+d_{z})}, \\ G_{zyx}&:\,=G_{zy}G_{yx},&G_{z-x}&:\,=G_{zy}G_{yx}\frac{d_{y}}{(d_{x}+d_{z})}, \end{aligned}$$

and the loop gains as

$$\begin{aligned} L_{x}&:\,=\frac{k_{xz}k_{zy}k_{yx}}{d_{x}(d_{x}+d_{y})(d_{x}+d_{z})}&L_{y}&:\,=\frac{k_{xz}k_{zy}k_{yx}}{(d_{x}+d_{y})d_{y}(d_{y}+d_{z})} \\ L_{z}&:\,=\frac{k_{xz}k_{zy}k_{yx}}{(d_{x}+d_{z})(d_{y}+d_{z})d_{z}},&L_{xyz}&= \frac{k_{xz}k_{zy}k_{yx}}{(d_{x}+d_{y})(d_{y}+d_{z})(d_{z}+d_{x})},\\ L_{mix}&:\,=G_{xz}G_{zy}G_{yx}=\frac{L_{x}L_{y}L_{z}}{L_{xyz}} \end{aligned}$$

Because $L_{mix}$ can be obtained from the other loop gains, we effectively have four loop gains in this network.

Appendix 3: Variance Decomposition of the FB Network with Two Components

We derive the variance decomposition for the FB network with two components via the linearization by Lyapunov equation. Let us represent the solution of the Lyapunov equation with the corresponding linear stochastic differential equation as Eq. (48). $\xi _{x}(t)$ and $\xi _{y}(t)$ are the fluctuation of x and y around their averages. For notational simplicity below, we identify $\xi _{x}(t)$ and $\xi _{y}(t)$ with x(t) and y(t) because their difference are constants. We discretize Eq. (48) for x(t) and y(t) by conditional propabilities as

$$\begin{aligned} \mathbb {P}(y_{t+\Delta t}|x_{t},y_{t})&\approx \mathbb {P}_{G}(y_{t+\Delta t}; (1-d_{y}\Delta t)y_{t}+ k_{yx}x_{t}\Delta t, D_{y}\Delta t), \nonumber \\ \mathbb {P}(x_{t+\Delta t}|x_{t},y_{t+\Delta t})&\approx \mathbb {P}_{G}(x_{t+\Delta t}; (1-d_{x}\Delta t)x_{t}+ k_{xy}y_{t}\Delta t, D_{x}\Delta t), \end{aligned}$$

(56)

where $\mathbb {P}_{G}(x; \mu , \sigma ^{2})$ is the Gaussian distribution for x whose mean and variance are $\mu$ and $\sigma ^{2}$. Let $\mathcal {X}_{t}$ be the discretized history of x(t) as $\mathcal {X}_{t}:\,=\{\ldots , x_{0}, \ldots , x_{t-\Delta t}, x_{t}\}$. The conditional probability $\mathbb {P}(y_{t}|\mathcal {X}_{t})$ satisfies the following sequential Bayes theorem:

$$\begin{aligned} \displaystyle \mathbb {P}(y_{t+\Delta t}|\mathcal {X}_{t+\Delta t})=\frac{\mathbb {P}(x_{t+\Delta t}|x_{t},y_{t+\Delta t}) \displaystyle \sum _{y_{t}}\mathbb {P}(y_{t+\Delta t}|x_{t},y_{t})\mathbb {P}(y_{t}|\mathcal {X}_{t})}{\displaystyle \sum _{y_{t+\Delta t}}\mathbb {P}(x_{t+\Delta t}|x_{t},y_{t+\Delta t}) \displaystyle \sum _{y_{t}}\mathbb {P}(y_{t+\Delta t}|x_{t},y_{t})\mathbb {P}(y_{t}|\mathcal {X}_{t})}, \end{aligned}$$

(57)

Because the stationary solution of the linear stochastic differential equation is Gaussian, $\mathbb {P}(y_{t}|\mathcal {X}_{t})$ can be parametrized as $\mathbb {P}(y_{t}|\mathcal {X}_{t}) = \mathbb {P}_{G}(y_{t}; \mu _{y}(t), \Sigma _{y}(t))$. By inserting this and Eq. (56) into Eq. (57) and by taking the limit of $\Delta t\rightarrow 0$, we obtain stochastic differential equations as

$$\begin{aligned} \mathrm {d}\mu _{y}(t)&= (k_{yx} x(t) - d_{y} \mu _{y}(t))\mathrm {d}t+ \frac{k_{xy}}{D_{x}} \Sigma _{y}(t)\left[ \mathrm {d}x(t) -(k_{xy} \mu _{y}(t)-d_{x} x(t))\mathrm {d}t\right] ,\end{aligned}$$

(58)

$$\begin{aligned} \mathrm {d}\Sigma _{y}(t)&=\left[ -2 d_{y}\Sigma _{y}(t)-\frac{k_{xy}^{2} \Sigma _{y}^{2}(t)}{D_{x}}+ D_{y}\right] \mathrm {d}t. \end{aligned}$$

(59)

This is a version of Kalman-Bucy filter with feedback. Because $\Sigma _{y}(t)$ depends only on parameters, its positive stationary solution becomes

$$\begin{aligned} \bar{\Sigma }_{y}=2 \frac{d_{x}d_{y}}{k_{xy}^{2}}\left[ -1 + \sqrt{1 + \frac{k_{xy}^{2}}{d_{x}d_{y}}\frac{G_{yy}\bar{y}}{G_{xx}\bar{x}}} \right] G_{xx}\bar{x}\le G_{yy}\bar{y}. \end{aligned}$$

(60)

where we use $D_{x}=2 \bar{a}_{x}=2 d_{x}G_{xx}\bar{x}$ and $D_{y}=2 \bar{a}_{y}=2 d_{y}G_{yy}\bar{y}$, and the inequality is obtained from Eq. (59). Because $\Sigma _{y}(t) = \mathbb {V}[y_{t}|\mathcal {X}_{t}]$, we obtain

$$\begin{aligned} \mathbb {E}[\mathbb {V}[y_{t}|\mathcal {X}_{t}]]=2 \frac{d_{x}d_{y}}{k_{xy}^{2}}\left[ -1 + \sqrt{1 + \frac{k_{xy}^{2}}{d_{x}d_{y}}\frac{G_{yy}\bar{y}}{G_{xx}\bar{x}}} \right] G_{xx}\bar{x}. \end{aligned}$$

(61)

for the stationary state. It should be noted that Eq. (61) is independent of $k_{yx}$ that characterizes the feedback strength from x to y. Similarly, we also obtain

$$\begin{aligned} \mathbb {E}[\mathbb {V}[x_{t}|\mathcal {Y}_{t}]]=2 \frac{d_{x}d_{y}}{k_{yx}^{2}}\left[ -1 + \sqrt{1 + \frac{k_{yx}^{2}}{d_{x}d_{y}}\frac{G_{xx}\bar{x}}{G_{yy}\bar{y}}} \right] G_{yy}\bar{y}. \end{aligned}$$

(62)

Appendix 4: Variance Decomposition of the FF Network with Two Components

We verify that our analytic derivation of the variance decomposition for the FB network include the decomposition of the FF network as a special case. For $k_{xy}=0$, i.e., there is no feedback from y to x, we can reduce Eqs (58) and (59) as

$$\begin{aligned} \mathrm {d}\mu _{y}(t)&= (k_{yx} x(t) - d_{y} \mu _{y}(t))\mathrm {d}t\end{aligned}$$

(63)

$$\begin{aligned} \mathrm {d}\Sigma _{y}(t)&=\left[ -2 d_{y}\Sigma _{y}(t)+ D_{y}\right] \mathrm {d}t. \end{aligned}$$

(64)

Thus, we have

$$\begin{aligned} \mathbb {E}[y_{t}|\mathcal {X}_{t}]&=\mu _{y}(t)=e^{-d_{y} t}\left[ y(0) + k_{yx} \int _{0}^{t} x(t')\mathrm {d}t'\right] ,\end{aligned}$$

(65)

$$\begin{aligned} \mathbb {V}[y_{t}|\mathcal {X}_{t}]&=\Sigma _{y}(t)=G_{yy}\bar{y}\left[ 1 - e^{-2 d_{y}t}\right] . \end{aligned}$$

(66)

From this, we can recover the variance decomposition for the stationary state as

$$\begin{aligned} \mathbb {V}[\mathbb {E}[y_{t}|\mathcal {X}_{t}]]&= \frac{k_{yx}^{2}}{(d_{x}+d_{y})d_{y}}G_{xx}\bar{x},\end{aligned}$$

(67)

$$\begin{aligned} \mathbb {E}[\mathbb {V}[y_{t}|\mathcal {X}_{t}]]&=G_{yy}\bar{y} \end{aligned}$$

(68)

Appendix 5: Generalized Variance Decomposition of a FF Network with Three Components

For the FF network depicted in Fig. 3a, the generalized variance decomposition of $\sigma _{y}^{2}$ [4] can also be described as

$$\begin{aligned} \sigma _{y}^{2}&=\underbrace{\mathbb {E}[\mathbb {V}[y(t)|\{\mathcal {X}(t),\mathcal {Y}'(t)\}]]}_{(II)} + \underbrace{\mathbb {E}[\mathbb {V}[\mathbb {E}[y(t)|\{\mathcal {X}(t),\mathcal {Y}'(t)\}]|\mathcal {Y}'(t)]]}_{(III)} + \underbrace{\mathbb {V}[\mathbb {E}[y(t)|\mathcal {Y}'(t)]]}_{(V)}. \end{aligned}$$

(69)

We show here that the terms (II), (III) and (V) are the same as those in the source decomposition shown in Eq. (25). We derive the correspondence under the assumption of the stationarity and linearization of the network dynamics because the source decomposition requires these assumptions.

Because of the cascading relation, $y' \rightarrow x \rightarrow y$, $\mathbb {E}[\mathbb {V}[y(t)|\{\mathcal {X}(t),\mathcal {Y}'(t)\}]]$ is simplified as $\mathbb {E}[\mathbb {V}[y(t)|\{\mathcal {X}(t),\mathcal {Y}'(t)\}]]=\mathbb {E}[\mathbb {V}[y(t)|\{\mathcal {X}(t)\}]]$. From Eq. (66) obtained for the two components FF network, we can see that $\mathbb {V}[y(t)|\{\mathcal {X}(t)\}] = G_{yy}\bar{y}$ for the stationary condition irrespective of the dynamics of x(t). Thus, we have $\mathbb {E}[\mathbb {V}[y(t)|\{\mathcal {X}(t)\}]]=G_{yy}\bar{y}$, which is the same as the term (II) in Eq. (25).

Because $y'$ is the upstream of the cascade, its fluctuation is determined only by $W_{y'}(t)$ in the linearized stochastic differential equation, Eq. (48), as

$$\begin{aligned} \mathrm {d}\xi _{y'}(t)&= K_{y'y'}(\bar{\mathbf {n}}) \xi _{y'}\mathrm {d}t+\sqrt{D(\bar{\mathbf {n}})_{y'}}\mathrm {d}W_{y'}(t), \end{aligned}$$

(70)

where we identified the indices $i=\{1,2,3\}$ in Eq. (48) with $i=\{y',x,y\}$ for readability. If we are given a realization of $W_{y'}(t)$, then the history of $\xi _{y'}(t)$, $\Xi _{y'}(t):\,=\{\xi _{y'}(t')|t' \in [0,t]\}$, is obtained deterministically as the function of $W_{y'}(t)$ by solving this equation. Thus, we have $\mathbb {V}[\mathbb {E}[y(t)|\mathcal {Y}'(t)]]=\mathbb {V}[\mathbb {E}[y(t)|\Xi _{y'}(t)]]=\mathbb {V}[\mathbb {E}[\xi _{y}(t)|\mathcal {W}_{y'}(t)]]$. Because this is the term of source decomposition shown in Eq. (50), $\mathbb {V}[\mathbb {E}[y(t)|\mathcal {Y}'(t)]]$ corresponds to the term (V) in Eq. (25). Note that the explicit representation of the terms in Eq. (69) was also obtained in [4].