Abstract
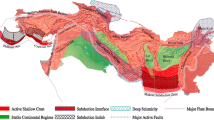
The Seismic Hazard Harmonization in Europe (SHARE) project, which began in June 2009, aims at establishing new standards for probabilistic seismic hazard assessment in the Euro-Mediterranean region. In this context, a logic tree for ground-motion prediction in Europe has been constructed. Ground-motion prediction equations (GMPEs) and weights have been determined so that the logic tree captures epistemic uncertainty in ground-motion prediction for six different tectonic regimes in Europe. Here we present the strategy that we adopted to build such a logic tree. This strategy has the particularity of combining two complementary and independent approaches: expert judgment and data testing. A set of six experts was asked to weight pre-selected GMPEs while the ability of these GMPEs to predict available data was evaluated with the method of Scherbaum et al. (Bull Seismol Soc Am 99:3234–3247, 2009). Results of both approaches were taken into account to commonly select the smallest set of GMPEs to capture the uncertainty in ground-motion prediction in Europe. For stable continental regions, two models, both from eastern North America, have been selected for shields, and three GMPEs from active shallow crustal regions have been added for continental crust. For subduction zones, four models, all non-European, have been chosen. Finally, for active shallow crustal regions, we selected four models, each of them from a different host region but only two of them were kept for long periods. In most cases, a common agreement has been also reached for the weights. In case of divergence, a sensitivity analysis of the weights on the seismic hazard has been conducted, showing that once the GMPEs have been selected, the associated set of weights has a smaller influence on the hazard.




Similar content being viewed by others
References
Abrahamson NA, Shedlock KM (1997) Overview. Seismol Res Lett 68:9–23
Abrahamson NA, Silva WJ (2008) Summary of the Abrahamson & Silva NGA ground motion relations. Earthq Spectra 24:67–97
Akkar S, Bommer JJ (2010) Empirical equations for the prediction of PGA, PGV, and spectral accelerations in Europe, the Mediterranean Region, and the Middle East. Seismol Res Lett 81:195–206
Akkar S, Çağnan Z, Yenier E, Erdoğan Ö, Sandikkaya MA, Gülkan P (2010) The recently compiled Turkish strong-motion database: preliminary investigation for seismological parameters. J Seismol 14:457–479
Allen TI, Wald DJ (2009) Evaluation of ground-motion modeling techniques for use in global shakemap—a critique of instrumental ground-motion prediction equations, peak ground motion to macroseismic intensity conversions, and macroseismic intensity predictions in different tectonic settings. US Geological Survey Open-File Report 2009-1047, p 114
Ambraseys N, Smit P, Douglas J, Margaris B, Sigbjornsson R, Olafsson S, Suhadolc P, Costa G (2004) Internet-site for European strong-motion data. Boll Geofis Teor Appl 45:113–129
Ambraseys NN, Simpson KA, Bommer JJ (1996) Prediction of horizontal response spectra in Europe. Earthquake Eng Struct Dyn 25:371–400
Ambraseys NN, Douglas J, Sarma SK, Smit PM (2005) Equation for the estimation of strong ground motions from shallow crustal earthquakes using data from Europe and the Middle East: horizontal peak ground acceleration and spectral acceleration. Bull Earthquake Eng 3:1–53
Atkinson GM (2008) Ground-motion prediction equations for eastern north America from a referenced empirical approach: implications for epistemic uncertainty. Bull Seismol Soc Am 98:1304–1318
Atkinson GM, Boore DM (2003) Empirical ground-motion relations for subduction zone earthquakes and their application to Cascadia and other regions. Bull Seismol Soc Am 93:1703–1729
Atkinson GM, Boore DM (2006) Earthquake ground-motion prediction equations for eastern north America. Bull Seismol Soc Am 96:2181–2205
Atkinson GM, Macias M (2009) Predicted ground motions for great interface earthquakes in the Cascadia subduction zone. Bull Seismol Soc Am 99:1552–1578
Atkinson GM, Morrison M (2009) Observations on regional variability in ground-motion amplitudes for small-to-moderate earthquakes in north America. Bull Seismol Soc Am 99:2393–2409
Beauval C, Bard P-Y, Hainzl S, Guéguen P (2008) Can strong motion observations be used to constrain probabilistic seismic hazard estimates? Bull Seismol Soc Am 98:509–520
Beauval C, Theodulidis N, Delavaud E, Cotton F (2012) GMPEs for PSHA calculations: the case of the Greek subduction zone (and other zones around the world). In: Proceedings of the 15th world conference on earthquake engineering, 24–28 September, Lisbon, Portugal
Berge-Thierry C, Cotton F, Scotti O, Griot-Pommera DA, Fukushima Y (2003) New empirical response spectral attenuation laws for moderate European earthquakes. J Earthquake Eng 7:193–222
Beyer K, Bommer JJ (2006) Relationships between median values and between aleatory variabilities for different definitions of the horizontal component of motion. Bull Seismol Soc Am 96:1512–1522
Bindi D, Luzi L, Massa M, Pacor F (2010) Horizontal and vertical ground motion prediction equations derived from the Italian accelerometric archive (ITACA). Bull Earthquake Eng 8:1209–1230
Bommer JJ, Douglas J, Scherbaum F, Cotton F, Bungum H, Fäh D (2010) On the selection of ground-motion prediction equations for seismic hazard analysis. Seismol Res Lett 81:783–793
Bommer JJ, Douglas J, Strasser FO (2003) Style-of-faulting in ground-motion prediction equations. Bull Earthquake Eng 1:171–203
Bommer JJ, Scherbaum F (2008) The use and misuse of logic-trees in probabilistic seismic hazard analysis. Earthq Spectra 96:1967–1977
Bommer JJ, Stafford PJ, Alarcon JE, Akkar S (2007) The influence of magnitude range on empirical ground-motion prediction. Bull Seismol Soc Am 97:2152–2170
Boore DM, Atkinson GM (2008) Ground motion prediction equations for the average horizontal component of PGA, PGV, and 5%-Damped PSA at spectral periods between 0.01 s and 10.0 s. Earthq Spectra 24:99–138
Budnitz RJ, Apostolakis G, Boore DM, Cluff LS, Coppersmith KJ, Cornell CA, Morris PA (1997) Recommendations for probabilistic seismic hazard analysis: guidance on uncertainty and use of experts, vol 1. NUREG/CR-6372, p 280
Burnham KP, Anderson DR (2002) Model selection and multimodel inference: a practical information-theoretic approach, 2nd edn. Springer, New York
Campbell KW (2003) Prediction of strong ground motion using the hybrid empirical method and its use in the development of ground-motion (attenuation) relations in eastern north America. Bull Seismol Soc Am 93:1012–1033
Campbell KW, Bozorgnia Y (2008) NGA ground motion model for the geometric mean horizontal component of PGA, PGV, PGD and 5%-damped linear elastic response spectra for periods ranging from 0.01 to 10 s. Earthq Spectra 24:139–171
Cauzzi C, Faccioli E (2008) Broadband (0.05 to 20 s) prediction of displacement response spectra based on worldwide digital records. J Seismol 12:453–475
Chiou BS-J, Darragh R, Gregor N, Silva W (2008) NGA project strong-motion database. Earthq Spectra 24:23–44
Chiou BS-J, Youngs RR (2008) An NGA model for the average horizontal component of peak ground motion and response spectra. Earthq Spectra 24:173–215
Chiou BS-J, Youngs RR, Abrahamson NA, Addo K (2010) Ground-motion attenuation model for small-to-moderate shallow crustal earthquakes in California and its implications on regionalization of ground-motion prediction models. Earthq Spectra 26:907–926
Cooke RG (1991) Experts in uncertainty: opinion and subjective probability in science. Oxford University Press, USA
Cornell CA (1968) Engineering seismic risk analysis. Bull Seismol Soc Am 58:1583–1606
Cotton F, Pousse G, Bonilla F, Scherbaum F (2008) On the discrepancy of recent European ground-motion observations and predictions from empirical models: analysis of KiK-net accelerometric data and point-sources stochastic simulations. Bull Seismol Soc Am 98:2244–2261
Cotton F, Scherbaum F, Bommer JJ, Bungum H (2006) Criteria for selecting and adjusting ground-motion models for specific target regions: application to central Europe and rock sites. J Seism 10:137–156
Danciu L, Tselentis G-A (2008) Engineering ground-motion parameters attenuation relationships for Greece. Bull Seismol Soc Am 97:162–183
Delavaud E, Scherbaum F, Kühn N, Allen T (2012) Testing the global applicability of ground motion prediction equations for active shallow crustal regions. Bull Seismol Soc Am (in press). doi:10.1785/0120110113
Douglas J (2008) Further errata of and additions to “ground motion estimation equations 1964-2003”. Final Report BRGM/RP-56187-FR, p 118
Douglas J (2011) Ground-motion prediction equations 1964–2010. Final Report BRGM/RP-59356-FR, p 446
Douglas J, Bungum H, Scherbaum F (2006) Ground-motion prediction equations for Southern Spain and Southern Norway obtained using the composite hybrid model perspective. J Earthquake Eng 10:33–72
Drouet S, Cotton F, Beauval C (2010) Deliverable 4.2: regionally adjusted ground motion prediction equations (GMPE) for Europe. Technical report, LGIT/CNRS/Universit Joseph Fourier, Grenoble, France. Report for the European project FP7-ENVIRONMENT-226967 “Seismic Hazard Harmonisation in Europe”, p 81
Drouet S, Scherbaum F, Cotton F, Souriau A (2007) Selection and ranking of ground motion models for seismic hazard analysis in the Pyrenees. J Seism 11:87–100
Faccioli E, Bianchini A, Villani M (2010) New ground motion prediction equations for t > 1 s and their influence on seismic hazard assessment. In: Proceedings of the University of Tokyo Symposium on Long-Period Ground Motion and Urban Disaster Mitigation, March 17–18, Tokyo, Japan
Faccioli E, Villani M (2009) Seismic hazard mapping for Italy in terms of broadband displacement response spectra. Earthquake Spectra 25:515–539
Garcia D, Singh SK, Herráiz M, Ordaz M, Pacheco JF (2005) Inslab earthquakes of central Mexico: peak ground-motion parameters and response spectra. Bull Seismol Soc Am 95:2272–2282
Goossens LHJ, Harper FT, Kraan BCP, Métivier H (2000) Expert judgment for a probabilistic accident consequence uncertainty analysis. Radiat Prot Dosim 90:295–301
Grünthal G, Arvidsson R, Bosse C (2010) Earthquake model for the European-Mediterranean region for the purpose of GEM1. GEM Scientific Technical Report STR10/04
Hiemer S, Wang Q, Jackson D, Kagan Y, Wiemer S, Zechar J Woessner J (2011) Stochastic earthquake source model: satisfying accepted laws. In: Abstract of STATSEI 7—7th international workshop on statistical seismology, Santorini, Greece
Idriss IM (2008) An NGA empirical model for estimating the horizontal spectral values generated by shallow crustal earthquakes. Earthquake Spectra 24:217–242
Jiménez MJ, Giardini D, Grünthal G, SESAME-Working-Group (2001) Unified seismic hazard modelling throughout the Mediterranean region. Boll Geof Teor Appl 42:3–18
Kaklamanos J, Baise LG, Boore DM (2011) Estimating unknown input parameters when implementing the NGA ground-motion prediction equations in engineering practice. Earthquake Spectra 27:1219–1235
Kalkan E, Gülkan P (2004) Empirical attenuation equations for vertical ground motion in Turkey. Earthquake Spectra 20:853–882
Kanno T, Narita A, Morikawa N, Fujirawa H, Fukushima Y (2006) A new attenuation relation for strong ground motion in Japan based on recorded data. Bull Seismol Soc Am 96:879–897
Lin P-S, Lee C-T (2008) Ground-motion attenuation relationships for subduction zone earthquakes in northeastern Taiwan. Bull Seismol Soc Am 98:220–240
Luzi L, Hailemikael S, Bindi D, Pacor F, Mele F, Sabetta F (2008) ITACA (Italian Accelerometric Archive): a web portal for the dissemination of Italian strong-motion data. Seism Res Lett 79:716–722
Massa M, Morasca P, Moratto L, Marzorati S, Costa G, Spallarossa D (2008) Empirical ground-motion prediction equations for northern Italy using weak- and strong-motion amplitudes, frequency content, and duration parameters. Bull Seismol Soc Am 98:1319–1342
McVerry GH, Zhao JX, Abrahamson NA, Somerville PG (2006) New Zealand acceleration response spectrum attenuation relations for crustal and subduction zone earthquakes. Bull NZ Soc Earthqu Eng 39:1–58
Montaldo V, Faccioli E, Zonno G, Akinci A, Malagnini L (2005) Treatment of ground-motion predictive relationships for the reference seismic hazard map of Italy. J Seism 9:295–316
Musson RMW (1999) Probabilistic seismic hazard maps for the north Balkan region. Annali Geofis 42:1109–1124
Özbey C, Sari A, Manuel L, Erdik M, Fahjan Y (2004) An empirical attenuation relationship for northwestern Turkey ground motion using a random effects approach. Soil Dyn Earthquake Eng 20:853–882
Pagani M, Monelli D, Crowley H, Danciu L, Field EH, Wiemer S, Giardini D (2010) GEM1 hazard: description of input models, calculation engine and main results. GEM Technical Report 2010-3. GEM Foundation, Pavia, Italy
Panko, KL, Pechmann JC (2004) The SEA99 ground-motion predictive relations for extensional tectonic regimes: revisions and a new peak ground velocity relation. Bull Seismol Soc Am 94:341–348
Papaioannou C, Papazachos C (2000) Time-independent and time-dependent seismic hazard in Greece based on seismogenic sources. Bull Seismol Soc Am 90:22–33
Sabetta F, Lucantoni A, Bungum H, Bommer JJ (2005) Sensitivity of PSHA results to ground motion prediction relations and logic-tree weights. Soil Dyn Earthquake Eng 55:317–329
Sandikkaya MA, Yilmaz MT, Bakir BS, Yilmaz Ö (2010) Site classification of Turkish national strong-motion stations. J Seism 14:543–563
Scasserra G, Stewart JP, Bazzurro P, Lanzo G, Mollaioli F (2009) A comparison of NGA ground-motion prediction equations to Italian data. Bull Seismol Soc Am 99:2961–2978
Scherbaum F, Bommer JJ, Bungum H, Cotton F, Abrahamson NA (2005) Composite ground-motion models and logic-trees: methodology. Bull Seismol Soc Am 95:1575–1593
Scherbaum F, Delavaud E, Riggelsen C (2009) Model selection in seismic hazard analysis: an information-theoretic perspective. Bull Seismol Soc Am 99:3234–3247
Scherbaum F, Kühn N (2011) Logic tree branch weights and probabilities: summing up to one is not enough. Earthquake Spectra 27:1237–1251
Sokolov V, Bonjer K-P, Wenzel F, Grecu B, Radulian M (2008) Ground-motion prediction equations for the intermediate depth vrancea (Romania) earthquakes. Bull Earthquake Eng 6:367–388
Tavakoli B, Pezeshk S (2005) Empirical-stochastic ground-motion prediction for eastern North America. Bull Seismol Soc Am 95:2283–2296
Toro GR, Abrahamson NA, Schneider JF (1997) Model of strong ground motions from earthquakes in central and eastern North America: best estimates and uncertainties. Seism Res Lett 68:41–57
Van Houtte C, Drouet C, Cotton F (2011) Analysis of the origins of κ (kappa) to compute hard rock to rock adjustment factors for GMPEs. Bull Seismol Soc Am 101:2926–2941
Youngs RR, Chiou BS-J, Silva WJ, Humphrey JR (1997) Strong ground motion attenuation relationships for subduction zone earthquakes. Seism Res Lett 68:58–73
Zhao JX, Zhang J, Asano A, Ohno Y, Oouchi T, Takahashi T, Ogawa H, Irikura K, Thio HK, Somerville P, Fukushima Y, Fukushima Y (2006) Attenuation relations of strong ground motion in Japan using site classification based on predominant period. Bull Seismol Soc Am 96:898–913
Acknowledgements
The main part of this work has been funded by the EC-Research Framework programme FP7, Seismic Hazard Harmonization in Europe, contract number 226967. The authors would like to warmly thank Julian Bommer, Hilmar Bungum, and Fabian Bonilla for their expert role and their key contribution to the ground-motion prediction equation evaluation and weighting. We thank an anonymous reviewer and Jochen Woessner for their comments on the first draft of this article. This paper also benefited from the feedbacks and interaction with Donat Fäh, Ben Edwards, Marco Pagani, Kyriazis Pitilakis, Pierre-Yves Bard, and Carola Di Alessandro. This work strongly benefited from the constant support of Jochen Woessner and Domenico Giardini, manager and coordinator of the SHARE FP7 project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Delavaud, E., Cotton, F., Akkar, S. et al. Toward a ground-motion logic tree for probabilistic seismic hazard assessment in Europe. J Seismol 16, 451–473 (2012). https://doi.org/10.1007/s10950-012-9281-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10950-012-9281-z