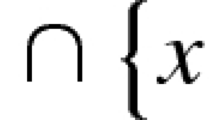Abstract
Let \(\mathcal{C}\) be a uniform clutter and let A be the incidence matrix of \(\mathcal{C}\) . We denote the column vectors of A by v 1,…,v q . Under certain conditions we prove that \(\mathcal{C}\) is vertex critical. If \(\mathcal{C}\) satisfies the max-flow min-cut property, we prove that A diagonalizes over ℤ to an identity matrix and that v 1,…,v q form a Hilbert basis. We also prove that if \(\mathcal{C}\) has a perfect matching such that \(\mathcal{C}\) has the packing property and its vertex covering number is equal to 2, then A diagonalizes over ℤ to an identity matrix. If A is a balanced matrix we prove that any regular triangulation of the cone generated by v 1,…,v q is unimodular. Some examples are presented to show that our results only hold for uniform clutters. These results are closely related to certain algebraic properties, such as the normality or torsion-freeness, of blowup algebras of edge ideals and to finitely generated abelian groups. They are also related to the theory of Gröbner bases of toric ideals and to Ehrhart rings.
Similar content being viewed by others
References
Blum S (2001) Base-sortable matroids and Koszulness of semigroup rings. Eur J Comb 22(7):937–951
Bruns W, Herzog J (1997) Cohen-Macaulay rings, revised edn. Cambridge University Press, Cambridge
Bruns W, Ichim B (2008) Normaliz 2.0, Computing normalizations of affine semigroups. Available from http://www.math.uos.de/normaliz
Conforti M, Cornuéjols G (1993) Clutters that pack and the max-flow min-cut property: a conjecture. In: Pulleyblank, WR, Shepherd, FB (eds) The fourth bellairs workshop on combinatorial optimization
Cornuéjols G (2001) Combinatorial optimization: Packing and covering. CBMS-NSF regional conference series in applied mathematics, vol 74. SIAM, Philadelphia
Escobar C, Martínez-Bernal J, Villarreal RH (2003) Relative volumes and minors in monomial subrings. Linear Algebra Appl 374:275–290
Escobar C, Villarreal RH, Yoshino Y (2006) Torsion freeness and normality of blowup rings of monomial ideals. In: Commutative algebra. Lect notes pure appl math, vol 244. Chapman & Hall/CRC, Boca Raton, pp 69–84
Gitler I, Valencia C (2005) Bounds for invariants of edge-rings. Commun Algebra 33:1603–1616
Gitler I, Valencia C, Villarreal RH (2007) A note on Rees algebras and the MFMC property. Beitr Algebra Geom 48(1):141–150
Gitler I, Reyes E, Villarreal RH (2009) Blowup algebras of square–free monomial ideals and some links to combinatorial optimization problems. Rocky Mt J Math 39(1):71–102
Grayson D, Stillman M (1996) Macaulay2. Available via anonymous ftp from math.uiuc.edu
Harary F (1972) Graph theory. Addison-Wesley, Reading
Huneke C, Simis A, Vasconcelos WV (1989) Reduced normal cones are domains. Contemp Math 88:95–101
Jacobson N (1996) Basic algebra I, 2nd edn. Freeman, New York
Lehman A (1990) On the width-length inequality and degenerate projective planes. In: Cook W, Seymour P (eds) Polyhedral combinatorics. DIMACS series in discrete mathematics and theoretical computer science, vol 1. Am Math Soc, Providence, pp 101–105
Matsumura H (1980) Commutative algebra. Benjamin-Cummings, Reading
Schrijver A (2003) Combinatorial optimization. Algorithms and combinatorics, vol 24. Springer, Berlin
Stanley R (1996) Combinatorics and commutative algebra, 2nd edn. Birkhäuser, Boston
Sturmfels B (1996) Gröbner bases and convex polytopes. University lecture series, vol 8. Am Math Soc, Providence
Vasconcelos WV (2005) Integral closure. Springer monographs in mathematics. Springer, New York
Villarreal RH (2001) Monomial algebras. Monographs and textbooks in pure and applied mathematics, vol 238. Dekker, New York
Villarreal RH (2003) Monomial algebras and polyhedral geometry. In: Hazewinkel M (ed) Handbook of algebra, vol 3. Elsevier, Amsterdam, pp 257–314
Villarreal RH (2008a) Rees algebras and polyhedral cones of ideals of vertex covers of perfect graphs. J Algebr Comb 27(3):293–305
Villarreal RH (2008b) Rees cones and monomial rings of matroids. Linear Algebra Appl 428:2933–2940
Webster R (1994) Convexity. Oxford University Press, Oxford
Author information
Authors and Affiliations
Corresponding author
Additional information
The second author was partially supported by CONACyT grant 49251-F and SNI.
Rights and permissions
About this article
Cite this article
Dupont, L.A., Villarreal, R.H. Algebraic and combinatorial properties of ideals and algebras of uniform clutters of TDI systems. J Comb Optim 21, 269–292 (2011). https://doi.org/10.1007/s10878-009-9244-7
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10878-009-9244-7