Erlang loss models for the static deployment of ambulances

Abstract

How should one allocate a fleet of ambulances to fixed bases with the goal of keeping response times to calls as small as possible? We present two new models for this problem, both of which are based on the Erlang loss formula. The first model is stylized, and shows that allocating ambulances in proportion to the offered load is not necessarily optimal and can often be substantially improved upon. The second model can be used to screen potential allocations to try to identify top candidates for further investigation. Computational experiments on the first model provide insights on how we should modify ambulance allocations in response to different levels of offered load. Computational experiments on the second model compare this model with the so-called A-hypercube model and show that the our model has comparable, and in many cases, better performance in terms of the accuracy of the estimates of performance measures. Thus, our models can be used as pre-screening tools to identify promising ambulance allocations and these promising ambulance allocations can subsequently be evaluated carefully through simulation.

Appendices

Appendix A: Detailed derivation of approximation procedure

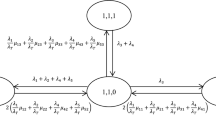
In this appendix we provide the derivation of a system of nonlinear equations that will yield, upon its solution, the probabilities s _jk that a call produced at zone j will be served by an ambulance stationed at base j(k).

Define, for all k = 1, ..., B + 1, $\mathcal A_{jk}(t)$ to be the event that the first k − 1 bases in demand node j’s ranking of bases are busy at time t. In other words, $\mathcal A_{jk}(t)$ is the event that none of the bases preferred to the k-th base in demand node j’s list has an available ambulance at time t. The event $\mathcal A_{j1}(t)$ has probability 1 by definition. If a call is generated at demand node j at time t, then on the event $\mathcal A_{jk}(t)$, the call is offered to base j(k). We write $\mathcal A_{jk}$ for $\mathcal A_{jk}(0)$ and let $a_{jk} = P(\mathcal A_{jk})$ be the stationary probability of the event $\mathcal A_{jk}(t)$. We can interpret a _jk as the probability that a call originating at demand node j will be offered to base j(k). (We are implicitly using a Poisson-arrivals-see-time-averages argument here to ensure that the Poisson arrivals at demand node j see the time-average behavior of the system. We also use the fact that the time-average behavior corresponds with the stationary behavior. For background on both of these topics, we refer the reader to Wolff [29].) Similarly, we let $\mathcal S_{jk}(t)$ denote the event that the first available ambulance in the priority list of bases j(1), ..., j(B) at time t is at j(k), and write $\mathcal S_{jk}$ for S _jk (0). Thus, as defined in Section 4 $s_{jk} = P(\mathcal S_{jk})$ is the probability that a call originating at node j will be answered by an ambulance from base j(k). We extend the definition of s _{j k} to include k = B + 1, so that s _{j, B + 1} is the probability that no ambulance is available anywhere.

We therefore turn to developing an approximation for the probabilities s _jk for all j = 1, ..., J, k = 1, ..., B. An approximation for s _j,B + 1 will follow from the fact that $\sum_{k=1}^{B+1} s_{j,k} = 1$, this being the probability that a call is either answered by one of the bases or lost.

We begin by noting that $\mathcal A_{j, k+1} \subseteq \mathcal A_{jk}$ and $\mathcal S_{jk} = \mathcal A_{jk} \backslash \mathcal A_{j,k+1}$ for all k = 1, ..., B. In other words, the first k bases on demand node j’s list can be busy only when the first k − 1 bases are busy, and a call is answered by the k-th base in demand node j’s list if and only if the first k − 1 bases are busy, but the k-th base is not. Hence, for k = 1,..., B, s _jk  = a _jk  − a _{j, k + 1}, $\mathcal A_{jk} = \cup_{i=k}^{B+1} \mathcal S_{ji}$, and $a_{jk} = \sum_{i=k}^{B+1} s_{ji}$ for all k = 1, ..., B. We let A and S respectively be the matrix of values {a _jk : j = 1, ...J,  k = 1, ..., B + 1} and { s _jk : j = 1, ...J,  k = 1, ..., B + 1}. Since we can recover either of these matrices from the other one, we focus on computing A through a fixed point equation.

Recall that a _j1 = 1 for all j = 1,...,J. To approximate a _j2, we first let λ _b be the “offered” load to base b, so that

$$\lambda_b = \sum\limits_{j=1}^J d_j \, a_{j, j^{-1}(b)},$$

(9)

where j ^− 1(b) stands for base b’s index in node j’s ranking. We then approximate a _j2, the probability that no ambulances are available at base j(1), by

$$a_{j2} \approx \mathcal E(n_{j(1)}, \lambda_{j(1)} / \mu_{j(1)}).$$

(10)

(The number of ambulances n _k and the service rate μ _k at base k are constants that do not change in our scheme.) It now remains to show how to compute approximations for a _jm for m > 2. The nested nature of the events $\mathcal A_{jm}$ for all m = 1,...,B ensures that we have

$$a_{jm} = P(\mathcal A_{j2}) \, P(\mathcal A_{j3} | \mathcal A_{j2}) \cdots P(\mathcal A_{jm} | \mathcal A_{j, m-1})$$

(11)

for m > 2. We approximate each factor of the form $P(\mathcal A_{j, k+1} | \mathcal A_{jk})$ by

$$P(\mathcal A_{j, k+1} | \mathcal A_{jk}) = \mathcal E(n_{j(k)}, \lambda(j,k) / \mu_{j(k)})$$

(12)

for all k = 2, ..., B, where λ(j, k) represents the conditional demand rate offered to base j(k), given $\mathcal A_{jk}$. By conditioning on $\mathcal A_{jk}$, the demand offered to base j(k) may not be Poisson, but we ignore this issue in our approximation. In analogy with (9), the conditional demand can be written as

$$\lambda(j, k) = \sum\limits_{i=1}^J d_i \, P(\mathcal A_{i, i^{-1}(j(k))} | \mathcal A_{jk}),$$

(13)

where i ^− 1(j(k)) is defined as the n for which i(n) = j(k), i.e., the index of base j(k) in demand node i’s list of bases. The probability in (13) is the conditional probability that a call originating at demand node i will be offered to base j(k), conditional on the first k − 1 bases in demand node j’s priority list being busy.

If all of the bases that appear before base j(k) in demand node i’s list also appear in demand node j’s list before base j(k), then we know that they are all busy, since we are conditioning on $\mathcal A_{jk}$. In that case, the conditional probability that the call originating at demand node i will be offered to base j(k) is 1. If not, then we essentially need to compute the probability that a subset of the bases are busy, given that another subset of the bases are busy. In principle, it is possible to include such probabilities as separate variables and to write linking equations for them. However, this would cause a dramatic increase in the number of variables. To produce a tractable set of equations, we instead adopt the following approximation.

For given demand nodes i, j and a given base j(k), we let n : = i ^− 1(j(k)), i.e., the index of base j(k) in node i’s list. In this case, since $\mathcal A_{in} = \cup_{m=n}^{B+1} \mathcal S_{im}$, we have

$$\begin{array}{rll}P(\mathcal A_{in}|\mathcal A_{jk}) &=& \frac{P(\mathcal A_{i n} \cap \mathcal A_{jk})}{P(\mathcal A_{jk})}\\ &=& \frac 1 {P(\mathcal A_{jk})} \, P \left( \cup_{m=n}^{B+1} \mathcal S_{im} \cap \mathcal A_{jk} \right).\end{array}$$

On the event $\mathcal A_{jk}$, bases j(1), ..., j(k − 1) are busy. Therefore, if base i(m) is contained in this list, then base i(m) cannot answer the call originating at demand node i. In such a case, we have $\mathcal S_{im} \cap \mathcal A_{jk} = \emptyset$. Consequently, we define the set $M = \big\{m: n \le m \le B+1,~ i(m) \notin \{j(1), \ldots, j(k-1)\} \big\}$ of bases that are not necessarily busy on the event $\mathcal A_{jk}$. In this case, we have

$$P(\mathcal A_{in}|\mathcal A_{jk}) = \frac 1 {P(\mathcal A_{jk})} \, P \left(\cup_{m \in M} \mathcal S_{im} \cap \mathcal A_{jk} \right),$$

(14)

where the numerator essentially states that a call originating at i must be answered by a base that is not busy, and therefore, not in the list of busy ambulances j(1), ..., j(k − 1). Finally, letting c ∧ d =  min {c, d}, we make the crude approximation that

$$\begin{array}{rll}P \left(\cup_{m \in M} \mathcal S_{im} \cap \mathcal A_{jk} \right) &\approx& \left( \textstyle \sum_{m \in M} P(\mathcal S_{im})\right) \wedge P(\mathcal A_{jk}) \\ &=& \left(\textstyle \sum_{m \in M} s_{im}\right) \wedge a_{jk}, \end{array}$$

which amounts to neglecting the “higher order” correction to $P(\mathcal S_{im})$ that comes from intersecting with $\mathcal A_{jk}$. Taking the minimum with a _jk ensures that (14) yields a result in [0, 1].

Combining (9)-(14) with the (linear) equations relating s _jk to a _jk , we obtain a system of equations for the entries of the matrix S that has the form S = f(S) for an appropriately specified function f. Thus, S is a fixed point of the system, and once we determine S, we can compute performance measures as described earlier.

Appendix B: Initializing the iterative procedure for solving the overflow model fixed-point equations

Here we comment on different ways to initialize the matrix S ⁰ at the start of the iterative procedure described in Section 4.

The solution matrix should satisfy $\sum_{k=1}^{B+1} s_{jk} = 1$ for every j = 1, ..., J, i.e., it is stochastic. So it is natural to choose an S ⁰ having this property as well. We tried 2 possibilities.

• 1. For each j = 1,...,J let $s^0_{j1}=1$ and $s^0_{jk}=0$ for k = 2,..., B + 1, i.e., allocate all of the demand coming from j to its preferred base.

• 2. For each j = 1, ..., J let $s^0_{jk}= \bar{\rho}^{\sum_{l=1}^{k-1} n_{j(l)}}(1- \bar{\rho}^{n_{j(k)}})$, for k = 1,...,B, and $s^0_{j,B+1} = 1 - \sum_{k=1}^N s^0_{jk}$ where $\bar{\rho}:=\lambda/N\mu$ is the average system utilization. Under the independent server approximation, the value of $s^0_{jk}$ corresponds to the probability that all bases preferred to j(k) in node j’s ranking are busy but base j(k) is not.

Appendix C: Detailed definition of function R(·)

Let R(S) : = (R(S)₁, R(S)₂, ..., R(S) _N ) where R(S) _v , for v = 1, ..., N represents the utilization of ambulance v. Denote by b = b(v) the base at which ambulance v is stationed, and by λ _b  = λ _b (S), the total demand offered to this base, as defined by Eq. 9; recall from Appendix A that $a_{jk}= \sum_{i=k}^{B+1} s_{ji}$. Then, according to the Erlang loss model, the utilization of each of the n _b ambulances stationed at base b equals the average expected utilization

$$R(S)_v = \frac 1{n_b}\sum\limits_{k=1}^{n_b} k \, P_{\mathcal E} (n_b, \lambda_b/\mu, k),$$

where

$$P_{\mathcal E}(n, \rho,k) = \frac {\rho^k/k!}{\sum_{j=0}^n \rho^j/j!}$$

is the Erlang probability that k out of the n ambulances are busy.