Bounding reasonable doubt: implications for plea bargaining

Abstract

A bound for reasonable doubt is offered based on the cost of type I and type II errors. The bound increases with the punishment, hence its use as a conviction threshold may leave too many offenders of severe crimes at large. Plea bargaining addresses this limitation but introduces strategic interaction between concerned parties. Considering strategic interaction between defendants and judge/jury, it is shown that to any plea offer there corresponds a unique equilibrium. Moreover, all equilibria share the same conviction threshold, given by the reasonable doubt bound. The latter property ensures that the plea bargaining procedure is consistent with the ‘equality before the law’ principle. The former property (that to any plea offer there corresponds a unique equilibrium) bears implications for the design of plea bargain schemes.

Appendices

Appendix 1: Defendant–judge/jury interaction

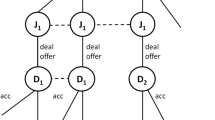
The interaction is analyzed as a signaling game between a type-t defendant, denoted D(t), and a judge/jury, denoted J, as follows (see Fig. 2). First, D(t) chooses $a_D\in \{TR,PB\}$, where TR means ‘go to trial’ and PB means ‘accept the plea offer’. If $a_D=PB$, D(t) receives the penalty Q(t) and the game ends. If $a_D=TR$, the defendant goes to trial. At the end of the trial a signal $\varepsilon$ is drawn from the distribution of ${\tilde{\varepsilon }}(t)$ and J (the judge or jury) chooses $a_J\in \{CO,AC\}$ after observing $\varepsilon$ and weighing in her belief regarding D(t)’s strategy, where CO means ‘convict’ and AC stands for ‘acquit’. The corresponding mix actions are $\alpha _D(\theta (t))=Pr\{a_D=TR|\theta (t)\}$ and $\alpha _J(\varepsilon ,a_D)=Pr\{a_J=CO|\varepsilon ,a_D\}$. At the time D(t) chooses $a_D$, he knows $\theta (t)\in \{G,I\}$ with certainty and ${\tilde{\varepsilon }}(t)$ up to the distribution $F^{\theta (t)}(\cdot ,t)$; at the time J chooses $a_J$, she observes $\varepsilon$ and knows $\theta (t)$ up to a guilt probability updated based on the observed signal $\varepsilon$ and her belief regarding $a_D$.

The expected payoff of D(t), at the time he chooses $a_D$, under the mixed actions $(\alpha _D,\alpha _J)$ is¹²

$$u_D(\alpha _D,{\bar{\alpha }}_J(\theta (t)),\theta (t))=\alpha _DE\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)\}(-\psi (P))+(1-\alpha _D)(-\psi (P)q(t)),$$

where ${\bar{\alpha }}_J(\theta (t))\equiv E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)\}$ is the pre-trial conviction probability of D(t) given $\theta (t)$, as perceived by D(t) before the trial, and, noting (5.2), $\psi (Q(t))=\psi (P)q(t)$.

J’s payoff at the time she chooses $a_J$ is

$$\begin{aligned} u_J(\alpha _D,\alpha _J(\varepsilon ),\theta (t))={\left\{ \begin{array}{ll}\alpha _D\alpha _J(\varepsilon )[-c_1(P)]+(1-\alpha _D)[-c_1(Q(t))]&{}{\text{if}}\;\theta (t)=I\\ (1-\alpha _D)[-c_2(P-Q(t))]&{}{\text{if}}\;\theta (t)=G\end{array}\right. } \end{aligned}$$

For example, in $u_J(\alpha _D,\alpha _J(\varepsilon ),G)$, with probability $\alpha _D\alpha _J(\varepsilon )$ the guilty defendant chooses to go to trial and is convicted, inflicting no social cost (the social cost of truthful conviction is normalized to zero) and with probability $1-\alpha _D$ the guilty defendant accepts the plea offer and receives the penalty $Q(t)<P$, inflicting the social cost $c_2(P-Q(t))$ associated with type II error (see Footnote 7).

D(t)’s strategy $\sigma _D(\cdot |\theta (t))$ sets a probability on $a_D=TR$ given $\theta (t)$; J’s strategy $\sigma _J(\cdot |a_D,\varepsilon )$ sets a probability on $a_J=CO$ given D(t)’s action $a_D$ and the observed trial signal $\varepsilon$. D(t)’s payoff under the strategy profile $(\sigma _D,\sigma _J)$ is

$$\begin{aligned} u_D(\sigma _D,\sigma _J,\theta )= & {} \sum _{a_D}\sum _{a_J}\sigma _D(a_D|\theta )\sigma _J(a_J|a_D,\varepsilon )u_D(a_D,a_J,\theta ) \\=\, & {} \alpha _DE\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)\}(-\psi (P))+(1-\alpha _D)(-\psi (P)q(t)). \end{aligned}$$

J’s payoff under the strategy $\sigma _J(\cdot |\varepsilon ,a_D)$ is

$$\Pi (\varepsilon ,t)\sum _{a_J}\sigma _J(a_J|a_D)u_J(a_D,a_J,G)+(1-\Pi (\varepsilon ,t))\sum _{a_J}\sigma _J(a_J|a_D)u_J(a_D,a_J,I),$$

where $\Pi (\varepsilon ,t)$, defined in (5.5), is the naïve guilt probability of D(t) at the conclusion of the trial, based on the observed signal $\varepsilon$ before J weighs in her belief regarding $a_D$.

A perfect Bayesian equilibrium (PBE) consists of $\sigma _D^*(\theta (t)),\,\theta (t)\in \{G,I\}$, ${\sigma _J^*(\varepsilon )}$ and posterior guilt probability $\Pi ^*(\varepsilon )$ such that:

$$\sigma _D^*(\theta (t))\in \arg \max _{\alpha _D}u_D(\alpha _D,E\{\alpha _J({\tilde{\varepsilon }})|\theta (t)\},\theta (t)),$$

(7.1)

$$\begin{aligned}& \sigma _J^*(\varepsilon )\in \arg \max _{\alpha _J(\varepsilon )}\Pi ^*(\varepsilon) \left[ \alpha _J(\varepsilon ) u_J(TR,CO,G)+(1-\alpha _J(\varepsilon ))u_J(TR,AC,G)\right] \\&\quad + (1-\Pi ^*(\varepsilon ))\left[ \alpha _J(\varepsilon )u_J(TR,CO,I)+(1-\alpha _J(\varepsilon ))u_J(TR,AC,I)\right] \end{aligned}$$

(7.2)

and

$$\Pi ^*(\varepsilon ) = \sigma _D^*(G)\Pi (\varepsilon ,t)/\left[ \sigma _D^*(G)\Pi (\varepsilon ,t)+\sigma _D^*(I)(1-\Pi (\varepsilon ,t))\right].$$

(7.3)

If the denominator on the right side of (7.3) vanishes, $\Pi ^*(\varepsilon )$ can be arbitrarily set between zero and 1. The updated guilt probability $\Pi ^*(\varepsilon )$ incorporates the observed trial signal $\varepsilon$ and J’s belief regarding the probability that D(t) chooses to go to trial.

Noting $u_D(\cdot )$, (7.1) gives

$$\begin{aligned} \sigma _D^*(G)= {\left\{ \begin{array}{ll}1&{}{\text{if}}\;E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}<q(t)\\ \in [0,1]&{}{\text{if}}\;E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}=q(t)\\ 0&{}{\text{if}}\;E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}>q(t)\end{array}\right. } \end{aligned}$$

(7.4a)

and

$$\begin{aligned} \sigma _D^*(I)= {\left\{ \begin{array}{ll}1&{}{\text{if}}\;E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=I\}<q(t)\\ \in [0,1]&{}{\text{if}}\;E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=I\}=q(t)\\ 0&{}{\text{if}}\;E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=I\}>q(t)\end{array}\right. }. \end{aligned}$$

(7.4b)

Noting $u_J(\cdot )$, (7.2) gives

$$\begin{aligned} \sigma _J^*(\varepsilon )={\left\{ \begin{array}{ll}1&{}{\text{if}}\;\Pi ^*(\varepsilon ) c_2(P)>(1-\Pi ^*(\varepsilon ))c_1(P)\\ 0&{}{\text{otherwise}}\end{array}\right. }. \end{aligned}$$

(7.5)

From (7.5) it is seen that J’s equilibrium strategy is to convict if

$$\Pi ^*(\varepsilon )/(1-\Pi ^*(\varepsilon ))>c_1(P)/c_2(P)$$

or, alternatively, if

$$\Pi ^*(\varepsilon )>[1+1/\varphi (P)]^{-1}\equiv b^*(P),$$

(7.6)

where $b^*(P)$ is the reasonable doubt bound defined in (4.3).

Let $r=(r^G,r^I)$, where $r^G$ and $r^I$ represent, respectively, J’s belief regarding the probability that D(t) chooses to go to trial if he is guilty or innocent. In a PBE, $r^*=(\sigma _D^*(G),\sigma _D^*(I))$, hence, noting (7.3),

$${\hat{\Pi }}(\varepsilon ,r^*,t)=\Pi ^*(\varepsilon )={\frac{r^{G*}\Pi (\varepsilon ,t)}{r^{G*}\Pi (\varepsilon ,t)+r^{I*}(1-\Pi (\varepsilon ,t))}},$$

(7.7)

verifying (5.7).

Appendix 2: Proof of Proposition 1

(i) We begin by showing:

Lemma 8.1

If $q(t)\in (0,\Pi ^G(t)]$, then

$$E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}=q(t)$$

(8.1)

must hold in a PBE.

Proof

Suppose $\alpha _J(\varepsilon )$ and $\alpha _D(\theta (t))$ constitute a PBE. From (7.5)–(7.6),

$$\begin{aligned} \alpha _J(\varepsilon )={\left\{ \begin{array}{ll}1&{}{\text{if}}\;\Pi ^*(\varepsilon )>b^*(P)\\ 0&{}{\text{otherwise}}\end{array}\right. } \end{aligned}$$

so

$$\begin{aligned} \alpha _J({\tilde{\varepsilon }}(t))={\left\{ \begin{array}{ll}1&{}{\text{if}}\;\Pi ^*({\tilde{\varepsilon }}(t))>b^*(P)\\ 0&{}{\text{otherwise}}\end{array}\right. }. \end{aligned}$$

(8.2)

Suppose $E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}<q(t)$. Since $\Pi (\varepsilon ,t)$ increases in $\varepsilon$ [cf. (5.6)], $\Pi ^*(\varepsilon )$ increases in $\varepsilon$ as well and $\alpha _J(\cdot )$ is nondecreasing. Condition (5.4) then implies that $E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=I\}<q(t)$ and (7.4) gives $\sigma _D(G)=\sigma _D(I)=1$, which in turn implies, noting (7.3) and (7.7), that $\Pi ^*(\varepsilon )=\Pi (\varepsilon ,t)$. Thus, (8.2) implies in this case

$$\begin{aligned} \alpha _J({\tilde{\varepsilon }}(t))={\left\{ \begin{array}{ll}1&{}{\text{if}}\;\Pi ({\tilde{\varepsilon }}(t),t)>b^*(P)\\ 0&{}{\text{otherwise}}\end{array}\right. } \end{aligned}$$

and, noting (5.10),

$$E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}=Pr\{\Pi ({\tilde{\varepsilon }}(t),t)>b^*(P)|\theta (t)=G\}\equiv \Pi ^G(t)\ge q(t),$$

a contradiction (since $q(t)\in (0,\Pi ^G(t)]$).

Suppose $E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}>q(t)$ and consider first $E\{\alpha _J({\tilde{\varepsilon }})|\theta (t)=I\}<q(t)$. Then, from (7.4), $\sigma _D^*(G)=0$, $\sigma _D^*(I)=1$ and (7.3) implies that $\Pi ^*(\varepsilon )=0$ identically at all $\varepsilon$. The conviction rule (7.6) then implies zero conviction probability, hence $\alpha _J({\tilde{\varepsilon }}(t))=0$ for all ${\tilde{\varepsilon }}(t)$ values and $E\{\alpha _J({\tilde{\varepsilon }}(t)|\theta (t)=G\}=0$—a contradiction.

The case $E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}>q(t)$ and $E\{\alpha _J({\tilde{\varepsilon }})|\theta (t)=I\}>q(t)$, under which guilty and innocent qualifiers accept the plea offer, can be ruled out noting that in this case $\sigma _D^*(G)=\sigma _D^*(I)=0$ and any $\Pi ^*(\varepsilon )\in [0,1]$ constitutes a PBE. Setting $\Pi ^*(\varepsilon )=0$ implies $\alpha _J({\tilde{\varepsilon }})=0$ and $E\{\alpha _J({\tilde{\varepsilon }}(t)|\theta =I\}=0< q(t)$—a contradiction. $\square$

It follows from Lemma 8.1 and (5.4), recalling that $\alpha _J(\cdot )$ is nondecreasing, that if $q(t)\in (0,\Pi ^G(t)]$, then

$$E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=I\}<E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}=q(t)$$

(8.3)

must hold in a PBE. Thus, noting (7.4), (8.3) gives

Lemma 8.2

If $q(t)\in (0,\Pi ^G(t)]$, then $r^{G*}\in (0,1]$ and ${r^{I*}=1}$.

In view of (7.7), in a PBE Eq. (8.2) can be rendered as

$$\begin{aligned} \alpha _J({\tilde{\varepsilon }}(t))={\left\{ \begin{array}{ll}1&{}{\text{if}}\;{\hat{\Pi }}({\tilde{\varepsilon }}(t),r^*,t)>b^*(P)\\ 0&{}{\text{otherwise}}\end{array}\right. } \end{aligned}$$

(8.4)

and condition (8.1) can be expressed as

$$Pr\left\{ {\hat{\Pi }}({\tilde{\varepsilon }}(t),r^*,t)>b^*(P)|\theta (t)=G\right\} =q(t),$$

(8.5)

verifying Property 4.

Noting (5.6) and (7.7), when $r^{G*}>0$, ${\hat{\Pi }}(\varepsilon ,r^*,t)$ increases from zero to one as $\varepsilon$ increases from its lower support −t to its upper suport $1-t$. Moreover, ${\hat{\Pi }}(\varepsilon ,r^*,t)$ increases from zero to $\Pi (\varepsilon ,t)$ as $r^{G*}$ increases from zero to one. For a given $q(t)\in (0,\Pi ^G(t)]$, these properties ensure the existence of ${\hat{\varepsilon }}<1-t$ and ${{\hat{r}}}^G\in (0,1]$ satisfying

$$Pr\{{\tilde{\varepsilon }}(t)>{\hat{\varepsilon }}|\theta (t)=G\}=q(t)$$

(8.6)

and

$${\hat{\Pi }}({\hat{\varepsilon }},({{\hat{r}}}^G,1),t)=b^*(P).$$

(8.7)

To see this, use the property that ${\hat{\Pi }}({\tilde{\varepsilon }}(t),({{\hat{r}}}^G,1),t)$ increases in $\tilde{\varepsilon }(t)$ to express (8.6) as

$$Pr\{{\hat{\Pi }}({\tilde{\varepsilon }}(t),({{\hat{r}}}^G,1),t)>{\hat{\Pi }}({\hat{\varepsilon }},({{\hat{r}}}^G,1),t)|\theta (t)=G\}=q(t),$$

which upon invoking (8.7) can be expressed as

$$Pr\{{\hat{\Pi }}({\tilde{\varepsilon }}(t),({{\hat{r}}}^G,1),t)>b^*(P)|\theta (t)=G\}=q(t).$$

(8.8)

Now, when $q(t)=\Pi ^G(t)$, Eqs. (5.10) and (8.8) ensure ${\hat{\Pi }}({\tilde{\varepsilon }}(t),(\hat{r}^G,1),t)=\Pi ({\tilde{\varepsilon }}(t),t)$, implying ${{\hat{r}}}^G=1$. Thus, (5.6) and $b^*(P)<1$ ensure the existence of ${\hat{\varepsilon }}<1-t$ that satisfies (8.6) when $q(t)=\Pi ^G(t)$. As q(t) decreases from $\Pi ^G(t)$ toward zero, Eq. (8.6) implies that ${\hat{\varepsilon }}$ must increase toward $1-t$ (the upper support of ${\tilde{\varepsilon }}(t)$). Equation (8.7) then implies, recalling that ${\hat{\Pi }}(\varepsilon ,(r^G,1),t)$ increases in both $\varepsilon$ and $r^G$, that ${{\hat{r}}}^G$ must decrease toward zero. We thus establish that

Lemma 8.3

$r^{G*}$ decreases from 1 toward 0 as q(t) decreases from $\Pi ^G(t)$ toward zero.

It follows from Lemmas 8.2 and 8.3 that to any $q(t)\in (0,\Pi ^G(t)]$ there corresponds a unique $r^*=(r^{G*},1)$ where $r^{G*}$ decreases from 1 toward zero as q(t) decreases from $\Pi ^G(t)$ toward zero. This completes the proof of part (i).

(ii) Suppose $q(t)>\Pi ^G(t)$. Then, repeating the arguments of Lemma 8.1 implies that in a PBE

$$E\{\alpha _J({\tilde{\varepsilon }}(t))|\theta (t)=G\}<q(t)$$

must hold. Equations (7.4), noting (5.4), then imply $\sigma _D^*(G)=\sigma _D^*(I)=1$. The intuition is obvious: if qualifying type-t defendants (guilty and innocent) prefer the trial over the plea bargain when $q(t)=\Pi ^G(t)$, they will certainly prefer to go to trial in less favorable plea offers $q(t)>\Pi ^G(t)$.