Waves of intermediate length through an array of vertical cylinders

Chiang C. Mei; I. -Chi Chan; Philip L. -F. Liu

doi:10.1007/s10652-013-9308-1

Environmental Fluid Mechanics

February 2014, Volume 14, Issue 1, pp 235–261 | Cite as

Waves of intermediate length through an array of vertical cylinders

Authors
Authors and affiliations

Chiang C. MeiEmail author
I. -Chi Chan
Philip L. -F. Liu

Original Article

First Online: 27 September 2013

Received: 31 May 2013

Accepted: 21 August 2013

589 Downloads
13 Citations

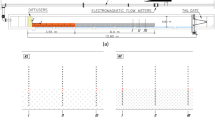
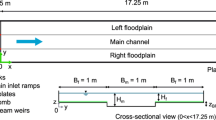
Abstract

We report a semi-analytical theory of wave propagation through a vegetated water. Our aim is to construct a mathematical model for waves propagating through a lattice-like array of vertical cylinders, where the macro-scale variation of waves is derived from the dynamics in the micro-scale cells. Assuming infinitesimal waves, periodic lattice configuration, and strong contrast between the lattice spacing and the typical wavelength, the perturbation theory of homogenization (multiple scales) is used to derive the effective equations governing the macro-scale wave dynamics. The constitutive coefficients are computed from the solution of micro-scale boundary-value problem for a finite number of unit cells. Eddy viscosity in a unit cell is determined by balancing the time-averaged rate of dissipation and the rate of work done by wave force on the forest at a finite number of macro stations. While the spirit is similar to RANS scheme, less computational effort is needed. Using one fitting parameter, the theory is used to simulate three existing experiments with encouraging results. Limitations of the present theory are also pointed out.

Keywords

Water Waves Vegetated Waters Coastal dynamics Tsunami Protection Theory of multiple scales Theory of homogenization Eddy Viscosity model

This is a preview of subscription content, to check access.

Notes

Acknowledgments

This work is supported by research grants from the National Science Foundation to Cornell University. CCM was also funded by a Mary Upson visiting professorship from Cornell University.

Appendix: A constant eddy viscosity model for wave scattering by a finite forest belt

For checking the numerical solution for variable $M$ and $N$ (see §7.1), we give the analytical solution for constant eddy viscosity.

The formal solutions in incidence zone and transmission zone are given by (7.2) and (7.3), respectively. For constant eddy viscosity in the forest region, $M$ and $N$ are complex constants. By separation of variables as for the open waters we obtain

$$\begin{aligned} \phi ^{\text {F}}(X,Z)=\sum _{q=0}^\infty \left[ C_q\cos (\gamma \hat{k}_q x)+D_q\sin (\gamma \hat{k}_q x)\right] \frac{\cosh \hat{k}_q(Z+h)}{\cosh \hat{k}_qh}, \end{aligned}$$

(A.1)

where $\gamma =\sqrt{(n+N)/(n+M)}$ and $\hat{k}_q$ are complex roots of the transcendental equation

$$\begin{aligned} 1={\left( 1+\frac{N}{n}\right) } \hat{k}_q\tanh \hat{k}_q h. \end{aligned}$$

(A.2)

Note that boundary conditions (6.14) and (6.15) have been used. $C_q$ and $D_q$ are coefficients to be determined.

Coefficients $B_p$, $C_q$, $D_q$, and $E_p$ are to be determined by matching the pressure and the horizontal velocity component at the interfaces between two adjacent regions. At $X=0$, the interfacial conditions are

$$\begin{aligned} \phi ^{\text {I}}=\phi ^{\text {F}},\quad -h<Z<0, \end{aligned}$$

(A.3)

$$\begin{aligned} \frac{\partial \phi ^{\text {I}}}{\partial X}=(n+M)\frac{\partial \phi ^{\text {F}}}{\partial X},\quad -h<Z<0. \end{aligned}$$

(A.4)

At $X=L_B$,

$$\begin{aligned}&\displaystyle \phi ^{\text {F}}=\phi ^{\text {T}},\quad -h<Z<0, \end{aligned}$$

(A.5)

$$\begin{aligned} (n+M)\frac{\partial \phi ^{\text {F}}}{\partial X}=\frac{\partial \phi ^{\text {T}}}{\partial X},\quad -h<Z<0. \end{aligned}$$

(A.6)

The following condition of orthogonality applies to both $k_p$ and $\hat{k}_q$:

$$\begin{aligned} \int _{-h}^0 \cosh {\kappa }_m (Z+h) \cosh {\kappa }_n (Z+h) dZ = \left\{ \begin{array}{ll} 0, &{} \quad m\ne n\\ \frac{2{\kappa }_m h+\sinh {2\kappa }_m h}{4{\kappa }_m}, &{} \quad m=n \end{array} \right. , \end{aligned}$$

(A.7)

where $\kappa =k$ or $\hat{k}$. By truncating the series and using (A.7) in (A.3) and (A.6), we obtain

$$\begin{aligned}&\displaystyle -\text {i} \frac{\Gamma _{0q}}{\cosh {k}_0 h} + \sum _{p=0}^{P_r}B_p \frac{\Gamma _{pq}}{\cosh {k}_p h} =C_q \frac{\Pi \left( \hat{k}_q\right) }{\cosh \hat{k}_qh},\quad q=0,1,2,\ldots ,Q, \end{aligned}$$

(A.8)

$$\begin{aligned} \frac{{k}_0 \Pi \left( {k}_0\right) }{\cosh {k}_0 h}\delta _{0p}-\text {i} B_p \frac{{k}_p \Pi \left( {k}_p\right) }{\cosh {k}_p h} =\gamma (n+M) \sum _{q=0}^Q D_q \frac{\hat{k}_q \Gamma _{pq}}{\cosh \hat{k}_qh},\quad p=0,1,2,\ldots ,P_r, \nonumber \\ \end{aligned}$$

(A.9)

at $X=0$, and

$$\begin{aligned} \left[ C_q\cos (\gamma \hat{k}_q L_B)+D_q\sin (\gamma \hat{k}_q L_B)\right] \frac{\Pi \left( \hat{k}_q\right) }{\cosh \hat{k}_qh} \nonumber \\ =\sum _{p=0}^{P_t} E_p e^{\text {i} {k}_p L_B} \frac{\Gamma _{pq}}{\cosh {k}_p h},\quad q=0,1,2,\ldots ,Q, \end{aligned}$$

(A.10)

$$\begin{aligned} \gamma (n+&M) \sum _{q=0}^Q \left[ -C_q\sin (\gamma \hat{k}_q L_B)+D_q\cos (\gamma \hat{k}_q L_B)\right] \frac{\hat{k}_q \Gamma _{pq}}{\cosh \hat{k}_qh} \nonumber \\&=\text {i} E_p e^{\text {i} {k}_p L_B} \frac{{k}_p \Pi \left( {k}_p\right) }{\cosh {k}_p h},\quad p=0,1,2,\ldots ,P_t, \end{aligned}$$

(A.11)

at $X=L_B$, where

$$\begin{aligned} \Gamma _{pq}&=\int _{-h}^0\cosh k_p(Z+h) \cosh \hat{k}_q(Z+h) dZ \nonumber \\&=\frac{k_p\sinh k_p h \cosh \hat{k}_q h-\hat{k}_q\cosh k_p h \sinh \hat{k}_q h}{k_p^2-\hat{k}_q^2}, \end{aligned}$$

(A.12)

$$\begin{aligned} \Pi (\kappa )=\frac{2{\kappa } h+\sinh {2\kappa } h}{4{\kappa }}, \quad \kappa =k_p, {\hat{k}}_q. \end{aligned}$$

(A.13)

In addition, $P_r$, $Q$, and, $P_t$ are the finite terms after truncation in zones (I), (F), and (T), respectively. The expansion coefficients $\left( B_p,C_q,D_q,E_p\right) $ can now be obtained by solving numerically the above algebraic equations. Afterwards, $|R|=|B_0|$ and $|T|=|E_0|$ are the reflection and transmission coefficients respectively.

References

1.
Asano T, Deguchi H, Kobayashi N (1992) Interactions between water waves and vegetation. Proc 23th Int Conf Coast Eng ASCE 3:2710–2723Google Scholar
2.
Augustin LN (2007) Laboratory experiments and numerical modeling of wave attenuation through artificial vegetation. MS Thesis, Texas A &M UniversityGoogle Scholar
3.
Augustin LN, Irish JL, Lynett P (2009) Laboratory and numerical studies of wave damping by emergent and near-emergent wetland vegetation. Coast Eng 56:332–340CrossRefGoogle Scholar
4.
Cheng N-S, Nguyen HT (2011) Hydraulic radius for evaluating resistance induced by simulated emergent vegetation in open-channel flows. J Hydraul Eng 137:995–1004CrossRefGoogle Scholar
5.
Dalrymple RA, Kirby JT, Hwang PA (1984) Wave refraction due to areas of energy dissipation. J Waterw Port Coast Ocean Eng 110:67–79CrossRefGoogle Scholar
6.
Dubi A, Tørum A (1994) Wave damping by kelp vegetation. Proc 24th Int Conf Coast Eng ASCE 1:142–156Google Scholar
7.
Fonsecaa MS, Cahalanb JA (1992) A preliminary evaluation of wave attenuation by four species of seagrass. Estuar Coast Shelf Sci 35:565–576CrossRefGoogle Scholar
8.
Harada K, Imamura F (2005) Effects of coastal forest on tsunami hazard mitigation—a preliminary investigation. In: Satake K (ed) Tsunamis: case studies and recent development. Advances in natural and technological hazards research, vol 23. Springer, Dordrecht, pp 279–292Google Scholar
9.
Hiraishi T, Harada K (2003) Greenbelt tsunami prevention in south-Pacific region. Rep Port Airpt Res Inst 43:1–23Google Scholar
10.
Huang Z, Yao Y, Sim SY, Yao Y (2011) Interaction of solitary waves with emergent rigid vegetation. Ocean Eng 38:1080–1088CrossRefGoogle Scholar
11.
Huang ZH, Zhang WB (2011) Wave attenuation through an array of rigid circular cylinders: a laboratory study. Asian Pac Coasts 2011:1826–1833Google Scholar
12.
Kobayashi N, Raichlen AW, Asano T (1993) Wave attenuation by vegetation. J Waterw Port Coast Ocean Eng 199:30–48CrossRefGoogle Scholar
13.
Li CW, Yan K (2007) Numerical investigation of wave–current–vegetation interaction. J Hydraul Eng 133:794–803CrossRefGoogle Scholar
14.
Liu D, Diplas P, Fairbanks JD, Hodges CC (2008) An experimental study of flow through rigid vegetation. J Geophys Res 113:F04015. doi: 10.1029/2008JF001042 CrossRefGoogle Scholar
15.
Lowe RJ, Koseff JR, Monismith (2005) Oscillatory flow through submerged canopies: 1. Velocity structure. J Geophys Res 110:C10016. doi: 10.1029/2004JC002788
16.
Massel SR, Furukawa K, Brinkman RM (1999) Surface wave propagation in mangrove forests. Fluid Dyn Res 24:219–249CrossRefGoogle Scholar
17.
Mazda Y, Kobashi D, Okada S (2005) Tidal-scale hydrodynamics within mangrove swamps. Wetl Ecol Manag 13:647–655CrossRefGoogle Scholar
18.
Mazda Y, Wolanski E, King B, Sase A, Ohtsuka D, Magi M (1997) Drag force due to vegetation in mangrove swamps. Mangrove Salt Marsh 1:193–199CrossRefGoogle Scholar
19.
Mei CC, Stiassnie M, Yue DKP (2005) Theory and applications of ocean surface waves. Part I: Linear aspects. Eq. (9.2.16). World Scientific, Singapore, p 458Google Scholar
20.
Mei CC, Black JL (1969) Scattering of surface waves by rectangular obstacles in waters of finite depth. J Fluid Mech 38:499–511CrossRefGoogle Scholar
21.
Mei CC, Chan I-C, Liu PL-F, Huang Z, Zhang W (2011) Long waves through emergent coastal vegetation. J Fluid Mech 461:461–491CrossRefGoogle Scholar
22.
Mendez FJ, Losada IJ (1999) Hydrodynamics induced by wind waves in a vegetation field. J Geophys Res 104:18383–18396. doi: 10.1029/1999JC900119 CrossRefGoogle Scholar
23.
Mendez FJ, Losada IJ (2004) An empirical model to estimate the propagation of random breaking and nonbreaking waves over vegetation fields. Coast Eng 51:103–118CrossRefGoogle Scholar
24.
Mo W (2010) Numerical investigation of solitary wave interaction with group of cylinders. Ph.D. Thesis, Cornell UniversityGoogle Scholar
25.
Morison JR, O’brien MP, Johnson JW, Schaaf SA (1950) The force exerted by surface waves on piles. Petrol Trans 189:149–154Google Scholar
26.
Nepf HM (1999) Drag, turbulence, and diffusion in flow through emergent vegetation. Water Resour Res 35:479–489CrossRefGoogle Scholar
27.
Raupach MR, Shaw RH (1982) Averaging procedures for flow within vegetation canopies. Bound Layer Meteorol 22:79–90CrossRefGoogle Scholar
28.
Sarpkaya T, Isaacson M (1981) Mechanics of wave forces on offshore structures. Van Nostrand Reinhold, New YorkGoogle Scholar
29.
Schutten J, Dainty J, Davy AJ (2004) Wave-induced hydraulic forces on submerged aquatic plants in shallow lakes. Ann Bot 93:333–341CrossRefGoogle Scholar
30.
Smagorinsky J (1963) General circulation experiments with the primitive equations. I. The basic experiment. Mon Weather Rev 91:99–164CrossRefGoogle Scholar
31.
Spalart PR, Allmaras SR (1994) A one-equation turbulence model for aerodynamic flows. La Recherche Aérospatiale 1:5–21Google Scholar
32.
Stoesser T, Kim SJ, Diplas P (2010) Turbulent flow through idealized emergent vegetation. J Hydraul Eng 136:1003–1017CrossRefGoogle Scholar
33.
Stratigaki V, Manca E, Prinos P, Losada IJ, Lara JL, Sclavo M, Amos CL, Cáceres I, Sánchez-Arcilla A (2011) Large-scale experiments on wave propagation over Posidonia oceanica. J Hydraul Res 49:31–43CrossRefGoogle Scholar
34.
Strusińska-Correia A, Husrin S, Oumeraci H (2013) Tsunami damping by mangrove forest: a laboratory study using parameterized trees. Nat Hazards Earth Syst Sci 13:483–503CrossRefGoogle Scholar
35.
Sumer BM, Fredsøe J (2006) Hydrodynamics around cylindrical structures. World Scientific, SingaporeGoogle Scholar
36.
Tanino Y, Nepf HM (2008) Lateral dispersion in random cylinder arrays at high Reynolds number. J Fluid Mech 600:339–371CrossRefGoogle Scholar
37.
Trowbridge J, Madsen OS (1984) Turbulent boundary layers: 1. Model formulation and first-order solution; 2. Second-order theory and mass transport. J Geophys Res 89(7989–7997):7999–8007CrossRefGoogle Scholar
38.
Tschirky P, Hall K, Turcke D (2000) Wave attenuation by emergent wetland vegetation. Proc 27th Int Conf Coast Eng ASCE 3:865–877Google Scholar
39.
Vo-Luong P, Massel S (2008) Energy dissipation in non-uniform mangrove forests of arbitrary depth. J Marine Syst 74:603–622CrossRefGoogle Scholar
40.
Wallace S, Cox R (2000) Effects of seagrass on nearshore current and wave dynamics. Proc 27th Int Conf Coast Eng ASCE 4:878–890Google Scholar
41.
Wu W et al (2011) Investigation of surge and wave reduction by vegetation. SERRI Report 80037–01. U.S. Department of Homeland SecurityGoogle Scholar
42.
Wu W, Zhang M, Ozeren Y, Wren D (2013) Analysis of vegetation effect on waves using a vertical 2D RANS model. J Coast Res 29:383–397CrossRefGoogle Scholar
43.
Zhong Z, Dai Y, Mei CC, Tong P (2002) A micromechanical theory of flow in pulmonary alveolar sheet. Comput Model Eng Sci 3:77–86Google Scholar

Copyright information

Authors and Affiliations

Chiang C. Mei
- 1
Email author
I. -Chi Chan
- 2
Philip L. -F. Liu
- 2
- 3

1.Department of Civil and Environmental EngineeringMassachusetts Institute of Technology CambridgeUSA
2.School of Civil and Environmental EngineeringCornell UniversityIthacaUSA
3.Institute of Hydrological and Oceanic SciencesNational Central UniversityJungliTaiwan

Waves of intermediate length through an array of vertical cylinders

Abstract

Keywords

Notes

Acknowledgments

References

Copyright information

Authors and Affiliations

Personalised recommendations

Cite article