Abstract
Based on insights into the nature of vocational mathematical knowledge, we designed a computer tool with which students in laboratory schools at senior secondary vocational school level could develop a better proficiency in the proportional reasoning involved in dilution. We did so because we had identified computations of concentrations of chemical substances after dilution as a problematic area in the vocational education of laboratory technicians. Pre- and post-test results indeed show that 47 students aged 16–23 significantly improved their proportional reasoning in this domain with brief instruction time (50–90 min). Effect sizes were mostly large. The approach of using a visual tool that foregrounds mathematical aspects of laboratory work thus illustrates how vocational mathematical knowledge can be developed effectively and efficiently.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Several characteristics of vocational mathematics—mathematics as used at work—have been formulated in the literature. A first characteristic is the situated nature of mathematical abstractions at work (Noss & Hoyles, 1996). Second, as observed by several scholars (e.g., Hoyles, Noss, Kent, & Bakker, 2010; Straesser, 2000) vocational mathematics is often mediated by technology. The work involving mathematics is further often scripted and spread out over socially distributed cognitive systems (Akkerman & Bakker, 2011; Hutchins, 1995). As a consequence of these characteristics, mathematics at work is often black-boxed (Williams & Wake, 2007) or invisible (Bakker, Hoyles, Kent, & Noss, 2006). However, this paper gives an example of vocational mathematics that is not black-boxed or invisible but explicitly carried out by employees: computing concentrations of chemical substances in a laboratory. The characteristic that we address here is the Janus-headed (two-faced) nature of vocational mathematics—in this case, both mathematical and chemical. From a mathematical perspective, the prototypical example of computations around dilution of samples is an application of proportional reasoning, a type of mathematical reasoning considered difficult for many students (Ben-Chaim, Fey, Fitzgerald, Benedetto, & Miller, 1998; Tourniaire & Pulos, 1985). From a chemical perspective, however, the focus is on determining the concentration of a substance in a liquid. In this process, a few simple arithmetical operations, such as division and multiplication, are carried out, but these are not considered mathematical by laboratory technicians (hereafter lab technicians). In a previous stage of our research, teachers and workplace supervisors stressed that many students and employees find the proportional reasoning involved in these chemical computations difficult.
The goal of the present article is to gain more insight into how such vocational mathematical knowledge at the service of workplace tasks can be developed—an area of research that has received little attention. As an exemplary case of the aforementioned characteristics of vocational mathematics, we addressed the major mathematical challenge identified in laboratory education—that of computations around dilution—by designing a dilution tool with accompanying learning tasks. One core work task is to produce solutions, carry out standardised analyses and tests, and report measure outcomes, occurrences and abnormalities (COLO, 2009). This often requires dilution accompanied by computations to determine the concentration of chemical substances in a sample. Given the limited amount of time available for disciplinary knowledge in Dutch competence-based vocational education, learning not only has to be effective but also efficient. The purpose of the research reported here was therefore to develop a learning environment in which students could effectively and efficiently learn the proportional reasoning required. We operationalised efficiency in terms of requiring short instruction times and requiring a relatively inexpensive computer tool, and we operationalised effectiveness as improvement in students’ test scores.
1 Theoretical background
From the above, it follows that an intervention aimed at developing such proportional reasoning should help to relate the arithmetical operations to the work-related actions of dilution. One advantage of computer tools is that they can assist in highlighting just those operations that designers intend students to engage with, while pushing to the background other, for example, chemical or practical reasons for dilution (e.g., the spectrophotometer being able to reliably measure only low concentrations). A second advantage of computer simulations is that time-consuming tasks can be speeded up so that students can concentrate on just those aspects of the key tasks they find difficult (cf. the approach taken in Bakker, Kent, Noss, & Hoyles (2009) and in Hoyles et al. (2010)). Furthermore, computer tools allow for making mistakes which, in a real laboratory, are to be prevented as much as possible.
In line with the literature on competence-based education (Van den Berg & De Bruijn, 2009) we assume that a clear link to tasks carried out by the profession stimulates learning because students can then better integrate the different types of knowledge involved (see also Coben, 2003). Van Merriënboer and Kirschner (2007) noted that students often complain about disconnected course modules and the lack of relevance of what they are supposed to learn for their future professions. They argue that avoiding compartmentalization and facilitating transfer requires taking a holistic view in instructional design. This entails that “instruction should ideally begin with a simplified but ‘whole’ model of reality, which is then conveyed to the learners according to sound pedagogical principles” (p. 9). Following this holistic view, a computer tool should focus on disciplinary knowledge such as mathematics in connection to core work tasks and give students the opportunity to integrate different types of knowledge (cf. Nab, Pilot, Brinkkemper, & Ten Berge, 2007).
However, even a holistic approach requires sequencing (Bakker & Derry, 2011). Because real-task environments may confront learners with a level of detail and work stress that interferes with learning, Van Merriënboer and Kirschner (2007) suggest several design features such as just-in-time procedural information and feedback. From their experience with promoting techno-mathematical literacies at work, Hoyles et al. (2010) concluded that learning tasks were more successful if the complexity of the underlying mathematics could be layered; that is, addressed in several stages of difficulty (for example, when reconstructing a pension scheme, the learning tasks started with regular premiums per month, postponing the influence of management charges and indexing to subsequent tasks). In the design of a computer tool for proportional reasoning in laboratories, we have drawn on these lessons. In this paper, we hypothesise that students can effectively and efficiently learn to compute concentrations with software that foregrounds proportional reasoning of a core work task, provides just-in-time help and layers the complexity of the vocational mathematics involved.
2 Methods
2.1 Computer tool and learning tasks
In collaboration with two teachers from two different laboratory schools (senior secondary vocational education), we designed a computer tool that simulated several authentic actions and computations involved in measuring concentrations of substances. This involves subtasks such as choosing an appropriate dilution factor, interpreting the scale strips and output of the spectrophotometer, using the extinction formula, and calculating the concentration backwards to determine the concentration in the original sample. The tool further offers help buttons for the main steps in the computations, and feedback on the correctness of students’ answers. Aiming for a layered progression from simple to more complex tasks and ideas, we ended up with five types of tasks that prepare students for the key working task mentioned in the qualification files (COLO, 2009).
-
1.
Measure the concentration of substance with a colour strip without dilution, like that used to measure the pH value of ditch water (Fig. 1).
-
2.
Dilute a sample (Fig. 2a, b). Here, by five times, before measuring concentration with a colour strip. In this case, the concentration found has to be multiplied by five to find the concentration in the sample.
-
3.
Dilute a sample so that extinction can be measured with a spectrophotometer. The extinction of the laser beam of a particular wave length is a measure of the concentration of a particular chemical substance (e.g., Potassium). Concentration can then be read from a graph (Fig. 3). Within a limited range, the relationship between concentration and extinction is linear; the constant k depends on the substance measured.
-
4.
Dilute a sample so that extinction can be measured with a spectrophotometer. Concentration can be calculated with the formula presented in the tool (Fig. 4).
-
5.
Repeated dilution (Fig. 5) is needed in order to measure extinction with the spectrophotometer.
A demonstration version in English, http://www.fi.uu.nl/toepassingen/00464/demo_en.html, provides one example of each type of task. The connecting thread through the increasingly complex tasks is the colour grading: Higher concentrations are represented by darker colours, and colour grading of the measurement strips in the first tasks moves down the extinction axis of the spectrophotometer graph as the concentration is reduced (see Fig. 3).
2.2 Participants and procedure
All participants were first-year students (aged 16–23), from three different schools, all studying to become lab technicians. Ten students with mixed academic abilities from school 1 worked in pairs to test the tool and accompanying tasks, and were interviewed afterwards. The insights gained in these trials were used as input for improving the tool and the tasks.
Students in schools 2 and 3 completed pre- and post-tests. Two classes from school 2 (inner city school) participated in a teaching experiment taught by their regular teacher who has a physics background. The two sessions with the computer tool in this school lasted 45 min each. We asked students to work through the series of tasks in pairs because there are indications that learning collaboratively has advantages for motivation and performance (e.g., Mercer & Littleton, 2007; Walter & Hart, 2009). Some students preferred to work individually (e.g., a few students with some form of autism—which, according to the teachers, is fairly common in laboratory education). At our request, the teacher started the second session with a 15-min discussion of two typical tasks involving dilution factors (items 1 and 2 of the pre-test).
One class from school 3 (rural area) worked through the learning tasks in 50 min without classroom discussion. Researchers were present in schools 1 and 2 but did not visit school 3. (For further information on the participants, see Table 1.)
2.3 Pre- and post-test
We used a pre- and post-test to determine learning effects. These tests consisted of four items and lasted up to 25 min (pre-test) and 20 min (post-test). In school 2, there were 6 weeks between the last lesson and the post-test; in school 3, there was only 1-week delay. Items 2 and 3 (Table 2) are similar to actions students had to perform with the computer tool. Item 1 was a different type of question: students start with a known quantity of a substance which they dissolve, as opposed to items 2 and 3, where students do not know the quantity and have to calculate backwards. Item 4 focuses on different actions: choosing a useful volumetric flask and pipette, and justifying the choice. The items in the pre- and post-test were pairwise similar, using only different substances and quantities. Four laboratory teachers independently judged the tests to be equally difficult.
2.4 Data collection
Students present in school 2 completed a pre- and/or post-test but not always both (presence during lessons was not obligatory). All students in school 2 who worked with the tool completed a form indicating for each task which steps they took to reach the final answer. In school 3, when no researchers were present, 24 students (16 females, eight males) worked with the computer tool and all completed both the pre-test and the post-test. In this school, no forms were completed.
2.5 Data analysis
First we compared the test results. We intended to use a t test to compare means of paired samples. However, this would require the test scores to be distributed normally—which they were not: The Kolmogorov–Smirnov test, valid for small samples (Field, 2005), indicated that this hypothesis was violated for all individual test items and overall test scores (significant at p = 0.00 for all items and overall score) at both schools 2 and 3. The distributions were fairly symmetrical but flatter than normal. We therefore used the non-parametric Wilcoxon signed ranks test for comparing pre- and post-test results per item and for the overall performance. To measure the magnitude of the observed effects, effect sizes were computed with SPSS. Effect size (here indicated with r) is the standardised mean difference (difference between means divided by the standard deviation). It is considered good practice to report this descriptive statistic in addition to significance because it allows the interpretation of the substantive rather than just statistical significance of a difference (Wilkinson & Task Force on Statistical Inference, 1999).
3 Results
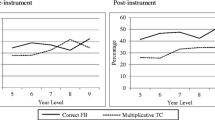
With a Wilcoxon signed ranks test, we checked whether the students scored significantly better on the post-test (one-tailed). Only the performances of students who completed both the pre- and the post-test were used. In school 2, this provided a sample of 23, with nine male and 14 female students. Statistics of both pre- and post-tests are provided in Table 3. Working on the tool for about 45 min on two occasions had a significant effect on test outcome (z = 3.18, p < 0.001, r = 0.47). The effect size (r = 0.47) shows an almost large effect (Cohen, 1992).
Because working with the tool had a significant effect on learning, it was interesting to explore on which items students improved their scores. The results of the Wilcoxon signed ranks tests per item can be found in Table 4. Students improved significantly on item 2 (z = 2.19, p < 0.05, r = 0.32), item 3 (z = 3.15, p < 0.01, r = 0.46), and item 4 (z = 2.80, p < 0.01, r = 0.41). Item 2 shows a medium effect size and both items 3 and 4 show medium to large effect sizes (Cohen, 1992). There was no statistically significant improvement on item 1, although students performed, on average, slightly better on the post-test with a medium effect size (see Table 4). The fact that the improvement on item 1 was not statistically significant can be the result of the small number of students involved or of the difference between item 1 on the test and the type of questions in the learning tasks in the tool. Item 1 of the pre-test was discussed in the second lesson, but in the learning tasks in the tool, students did not calculate concentrations in a dilution using the concentration in the chemical sample.
At school 3, we found similar results as in school 2, even though this third group used the tool for only 50 min and we, as researchers, were not around. The Wilcoxon test pointed to a significant difference between total scores on pre- and post-tests for 24 students (z(23) = 3.26, p < 0.05, r = 0.62). According to Field (2005), 0.50 is needed for large effect size, so r = 0.62 indicates a large effect size (Table 5). When breaking down the results per item, the results are similar to those in school 2: Again, improvement on item 1 was not statistically significant yet indicated a medium effect size. Differences in items 2 and 3 both showed large effect sizes (z(23) = 2.422, p < 0.05, r = 0.48 and z(23) = 2.625, p < 0.01, r = 0.53).
If we combine the data from schools 2 and 3 (N = 47), scores on all separate items and the total score differ significantly with α = 0.01 for all except item 1, which differs significantly at α = 0.05. The overall effect size of the combined data is 0.63, which is large.
4 Conclusion and discussion
Our hypothesis was that students can effectively and efficiently improve their proportional reasoning about concentrations with the software we designed. In this software, the computations were situated in the core work task of determining concentrations, just-in-time help and feedback was provided, and we layered the complexity involved, starting with simple colour strips and moving from using a graph to using a mathematical formula. As mentioned above, we operationalised efficiency in terms of requiring short instruction times and requiring a relatively inexpensive computer tool, and effectiveness as improvement in students’ test scores. The hypothesis is supported by the significant differences between overall scores on pre- and post-tests, and mostly the large effect sizes in both schools 2 and 3 which can be interpreted as a clear learning gain in brief periods of time. The computer tool, as tested here, was the result of about 300 h of programming, which we consider relatively inexpensive given the thousands of students who can use the tool freely online in the coming years.
The results on the different items differed. Given the similarity between items 2 and 3 with the tasks practised using the computer tool, it is not surprising that students showed larger improvement on those items. The content of item 4 is implicitly practised in the computer tasks, so more experience with such tasks might have stimulated the students to reflect more on the issues involved in choosing appropriate proportions of flasks and pipettes. The generally larger effect sizes in school 3 might be explained by the fact that it is in a rural area with fewer problems typical of inner-city schools, but we think that the most likely explanation is the briefer period between the learning session and the post-test (1 week instead of 6 weeks).
One might wonder how general the results are, given that we could not work with random samples of students. The results among schools 2 and 3, although in very different areas of the country (inner city and rural, respectively), were very similar, even at item levels. Moreover, our research did not focus on samples representative of populations, but on processes and propensities—the type of research that is much more common in education and psychology (Frick, 1998).
At the three different schools, teachers with different disciplinary backgrounds emphasised that the tool could be used well both in the mathematics and chemistry lessons, and even in other educational programmes such as pharmacy. One chemistry teacher said: “We normally wear blinkers. We only look for the chemistry, because teaching chemistry is our job. We do not look for the computations.” This suggests that the tool could function well at the boundary of these two disciplines, and appears to address the Janus-headed (two-faced) or hybrid nature of the knowledge developed here.
The proportional reasoning involved in determining concentrations after dilution is a typical case of reasoning with situated abstractions. At one point, our computer programmer exclaimed: “Why am I spending 300 hours of programming on one multiplication?” In his eyes, the mathematical core of the work task was just the multiplication of the concentration found and the dilution factor. However, when computing the original concentrations he, we, and many teachers we asked to work with the tool, often had to think hard about how to solve the concentration problems. The reason is that the context and language make it complex: What happens with the concentration if we take 50 ml out of a sample and add demineralised water to it until the 250-ml flask is full? Having limited knowledge of chemistry, we sometimes felt insecure about chemical reactions or processes that we might be unaware of. Discussions with chemistry teachers often ended up in despair because of the inherent confusion in language use. Is this a dilution factor of 5? 1/5? 1 + 4? 1 to 4? More generally, the computation is situated in a web of reasons (Bakker & Derry, 2011), many of which are chemical or practical, and only some of which are mathematical: We need to dilute because, otherwise, the spectrophotometer cannot measure reliably, but we should not arrive at too low a concentration, either. In practice, chemistry teachers tell their students not to measure too near the limits of the measurement range, so some estimation as to how much to dilute in the given context is also necessary.
In this article, we hope to have shown how vocational mathematical knowledge can be effectively and efficiently developed at school through the use of dedicated computer tools. Further research is needed to support this development in the actual workplace (e.g., pre- and post-tests were not possible in the research carried out by Hoyles et al. (2010)). Given that it would be expensive to develop such tools for all challenging mathematical aspects of occupations, one of the key questions for future research is therefore how situated and specific such tools need to be for particular learners and situations. In line with the work by Ainley, Pratt, and Hansen (2006) on purpose and utility, and of Dierdorp, Bakker, Eijkelhof, and van Maanen (2011) on adapting professional tasks to educational tasks, it would be interesting to test whether vocational contexts might help designers to connect student engagement and focus in task design in general education.
References
Ainley, J., Pratt, D., & Hansen, A. (2006). Connecting engagement and focus in pedagogic task design. British Educational Research Journal, 32, 21–36.
Akkerman, S. F., & Bakker, A. (2011). Crossing boundaries between school and work during apprenticeships. Vocations and Learning. doi:10.1007/s12186-011-9073-6.
Bakker, A., & Derry, J. (2011). Lessons from inferentialism for statistics education. Mathematical Thinking and Learning, 13, 5–26.
Bakker, A., Hoyles, C., Kent, P., & Noss, R. (2006). Improving work processes by making the invisible visible. Journal of Education and Work, 19, 343–361.
Bakker, A., Kent, P., Noss, R., & Hoyles, C. (2009). Alternative representations of statistical measures in computer tools to promote communication between employees in automotive manufacturing. Technology Innovations in Statistics Education, 3(2), 1–31. Retrieved from http://www.escholarship.org/uc/item/53b9122r.
Ben-Chaim, D., Fey, J. T., Fitzgerald, W. M., Benedetto, C., & Miller, J. (1998). Proportional reasoning among 7th grade students with different curricular experiences. Educational Studies in Mathematics, 36, 247–273.
Coben, D. (2003). Adult numeracy: Review of research and related literature. London: NRDC: National Research and Development Centre for adult literacy and numeracy.
Cohen, J. (1992). A power primer. Psychological Bulletin, 112, 155–159.
COLO. (2009). Landelijke kwalificaties MBO voor Analist [National qualifications MBO for lab technician]. Zoetermeer, The Netherlands: COLO.
Dierdorp, A., Bakker, A., Eijkelhof, H. M. C., & van Maanen, J. A. (2011). Authentic practices as contexts for learning to draw inferences beyond correlated data. Mathematical Thinking and Learning, 13, 132–151.
Field, A. (2005). Discovering statistics using SPSS (2nd ed.). London: Sage.
Frick, R. W. (1998). Interpreting statistical testing: Process and propensity, not population and random sampling. Behavior Research Methods, Instruments, and Computers, 30, 527–535.
Hoyles, C., Noss, R., Kent, P., & Bakker, A. (2010). Improving mathematics at work: The need for techno-mathematical literacies. London: Routledge.
Hutchins, E. (1995). Cognition in the wild. Cambridge: MIT Press.
Mercer, N., & Littleton, K. (2007). Dialogue and the development of children’s thinking: A sociocultural approach. London: Routledge.
Nab, J., Pilot, A., Brinkkemper, S., & Ten Berge, H. (2007). Authentic competence-based learning in university education in entrepreneurship. Utrecht: Utrecht University.
Noss, R., & Hoyles, C. (1996). Windows on mathematical meanings: Learning cultures and computers. Dordrecht: Kluwer Academic Press.
Straesser, R. (2000). Mathematical means and models from vocational contexts. A German perspective. In A. Bessot & J. Ridgway (Eds.), Education for mathematics in the workplace (pp. 65–80). Dordrecht: Kluwer.
Tourniaire, F., & Pulos, S. (1985). Proportional reasoning: A review of the literature. Educational Studies in Mathematics, 16, 181–204.
Van den Berg, N., & De Bruijn, E. (2009). Het glas vult zich. Kennis over de vormgeving en effecten van competentiegericht beroepsonderwijs; verslag van een review. [The glass is filling up. Knowledge about the design and effects of competence-based vocational education; A review study]. Amsterdam/’s-Hertogenbosch: ECBO.
Van Merriënboer, J. J. G., & Kirschner, P. A. (2007). Ten steps to complex learning: A systematic approach to four-component instructional design. New York: Erlbaum.
Walter, J. G., & Hart, J. (2009). Understanding the complexities of student motivations in mathematics learning. Journal of Mathematical Behavior, 28, 162–170.
Wilkinson, L., & Task Force on Statistical Inference. (1999). Statistical methods in psychology journals: Guidelines and explanations. American Psychologist, 54, 594–604.
Williams, J. S., & Wake, G. D. (2007). Black boxes in workplace mathematics. Educational Studies in Mathematics, 64, 317–343.
Acknowledgments
We thank teachers Ruud van Iterson (Drenthe College) and Paul Rutten (ROC Midden Nederland) for their valuable contribution to the design of the computer tool and learning tasks, and their students for participating in the research. We also thank Rob van de Vijver and his students (ROC Zeeland). We further gratefully acknowledge Bert Nijdam for his advice on the statistical analyses and Gail FitzSimons for carefully editing earlier versions of this manuscript.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
The research reported here was funded by NWO-PROO (411-06-205).
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Bakker, A., Groenveld, D., Wijers, M. et al. Proportional reasoning in the laboratory: an intervention study in vocational education. Educ Stud Math 86, 211–221 (2014). https://doi.org/10.1007/s10649-012-9393-y
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10649-012-9393-y