Abstract
The reported “hiatus” in the warming of the global climate system during this century has been the subject of intense scientific and public debate, with implications ranging from scientific understanding of the global climate sensitivity to the rate in which greenhouse gas emissions would need to be curbed in order to meet the United Nations global warming target. A number of scientific hypotheses have been put forward to explain the hiatus, including both physical climate processes and data artifacts. However, despite the intense focus on the hiatus in both the scientific and public arenas, rigorous statistical assessment of the uniqueness of the recent temperature time-series within the context of the long-term record has been limited. We apply a rigorous, comprehensive statistical analysis of global temperature data that goes beyond simple linear models to account for temporal dependence and selection effects. We use this framework to test whether the recent period has demonstrated i) a hiatus in the trend in global temperatures, ii) a temperature trend that is statistically distinct from trends prior to the hiatus period, iii) a “stalling” of the global mean temperature, and iv) a change in the distribution of the year-to-year temperature increases. We find compelling evidence that recent claims of a “hiatus” in global warming lack sound scientific basis. Our analysis reveals that there is no hiatus in the increase in the global mean temperature, no statistically significant difference in trends, no stalling of the global mean temperature, and no change in year-to-year temperature increases.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction, Motivation and Approach
The international debate on the “hiatus” in the warming of the global climate system over the last 15 years has intensified (e.g., Meehl et al. (2011), IPCC (2013), Otto et al. (2013), Fyfe et al. (2013), Kosaka and Xie (2013), Santer et al. (2014), Trenberth and Fasullo (2013), Smith (2013), Guemas et al. (2013), Chen and Tung (2014), Boykoff (2014), Hawkins et al. (2014), England et al. (2014), Karl et al. (2015), Cowtan et al. (2015)). The implications of the purported hiatus (also referred to as a “pause” or “slowdown”) are far reaching. First, contradictory scientific conclusions have emerged regarding the relationship between climate change and anthropogenic global warming, especially during a period of heightened carbon emissions (Kosaka and Xie 2013). Second, the discrepancy between climate model projections and observations appear to point to an overestimation of climate sensitivity to anthropogenic forcings (Otto et al. 2013; Fyfe et al. 2013).
The perceived hiatus has led to a myriad of resources being expended on trying to better understand the geophysical mechanisms that lead to a possible hiatus (including, among others, volcanic activity (Santer et al. 2014), Pacific Ocean variability (Kosaka and Xie 2013; Trenberth and Fasullo 2013), and increased ocean heat uptake (Smith 2013; Guemas et al. 2013; Chen and Tung 2014)), as well as spurious artifacts of the global climate observing system (Durack et al. 2014; Cowtan and Way 2014; Karl et al. 2015; Cowtan et al. 2015). The purported hiatus has therefore inspired valuable scientific insight into the processes that regulate decadal-scale variations of the climate system. However, the perception of a hiatus has important repercussions for public decision making, as the implications that global warming has paused or slowed down (Boykoff 2014; Hawkins et al. 2014), and that climate models have overestimated the rate of warming (e.g., Fyfe et al. (2013)), both influence the perceived level of mitigation action that is needed to obtain particular policy targets (Otto et al. 2013).
Fundamental to any work on the hiatus is to ascertain whether there is sufficient empirical evidence in support of its existence. Surprisingly, to our knowledge, a rigorous statistical analysis has not been undertaken, at least not one which incorporates temporal dependencies without making strong assumptions about the underlying process. Without empirical evidence in support of the hiatus claims, any further conclusions stemming from the assumption should be called into question.
As a part of our investigation to better understand the hiatus, we develop a comprehensive scientific framework that is intended to systematically test hypotheses that have been implied in statements claiming a hiatus in global warming. We first identify a typology of the scientific assertions that have been put forward, including i) that there has been a hiatus in the trend in global warming, ii) that there is a difference in trends before and during the hiatus, iii) that there has been a hiatus in the change in mean global temperature, and iv) that there is a difference in warming before and during the hiatus (when accounting for possibly non-linear increases without explicit reference to a linear trend). (See Supplementary Section 3.4 for more detail on the typology.) We next connect these scientific claims with four classes of distinct testable statistical hypotheses, with each hypothesis focusing on different aspects of the underlying (unknown) temperature process. We then identify and develop appropriate statistical tools in order to test each of these hypotheses in a principled manner, and under progressively less restrictive - and therefore more generally applicable-modeling assumptions, thereby allowing for a deeper understanding of the nuances of the global temperature time series. In particular, we attempt to properly account for temporal dependence, we use less restrictive resampling methods to assess statistical significance, and we employ a flexible nonparametric modeling approach. By applying these progressively more general techniques in a cascading approach, we are able to test the extent to which invalid statistical assumptions can lead to erroneous scientific conclusions.
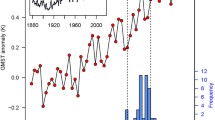
Our analysis is first undertaken using the NASA-GISS global mean land-ocean temperature index. It is subsequently also repeated on the NOAA and HadCRUT4 datasets for comparison purposes (see Supplemental Tables 1 and 2). The analysis is also undertaken on the recently released ERSSTv4 (Karl et al. (2015)) datasets (see Supplemental Tables 11 and 12). Plots of the NASA-GISS raw and smoothed global mean land-ocean temperature index from 1880 to 2013, with the base period 1951–1980, are given in in Fig. 1 (top). As there is a clear underlying trend, a moving average is superimposed on the time series. A statistical analysis of the serial correlation in the residuals after fitting a regression line is also given in Fig. 1 (top). The autocorrelation in the temperature time series is non-negligible. The presence of autocorrelation motivates the need to use less naive statistical methods to understand the evolution of temperature over time (see also Supplemental Section 2.2).
Top panel global mean land-ocean temperature index from 1880 to 2013, with base period 1951–1980 and moving average superimposed. The table provides Durbin-Watson and Ljung-Box p-values for the residuals from three OLS fits between 1950–2013. The Ljung-Box test here considers residual autocorrelation in the first 20 lags. The 1950–2013 Full OLS model fits a single regression line to all observations from 1950 to 2013. The 1950–2013 Separated model fits a separate regression line to the 1950–1997 and 1998–2013 periods. Bottom panel plot of the global mean land-ocean temperature index, from 1998 to 2013, with the ordinary least squares regression line superimposed
2 Methods
Datasets
The datasets of global surface temperature anomalies used in our analysis come from three sources: the NASA Goddard Institute for Space Studies (GISS) Surface Temperature Analysis (GISTEMP) Data, the NOAA National Climatic Data Center (NCDC) data, and the HadCRUT4 data, produced from the Met Office Hadley Centre in collaboration with the University of East Anglia Climatic Research Unit (CRU). Each source combines monthly land and sea surface temperature measurements into spatial grids that are then averaged into a single global temperature series. Temperature anomalies are computed from a baseline period, which differs by dataset. The differences in the three datasets largely come from the adjustment/infilling methods for sparse temporal/spatial coverage (Hansen et al. 2010; Morice et al. 2012). (See the Supplemental Section for more details). Note that given the global mean temperature data that is available, the main goal of our analysis is to understand the possible mischaracterizing of hiatus claims as compared to understanding the source of observational errors of the temperature process.
Temporal dependence and uncertainty quantification
The global temperature record exhibits temporal correlation. Standard statistical methods tend to ignore this important feature, which in turn can lead to incorrect statistical modeling assumptions and incorrect statistical significance, which can in turn lead to erroneous scientific conclusions. For the purposes of uncertainty quantification when testing each of the four statistical hypotheses, we either model the temporal dependence in the global temperature time series explicitly through a parametric autoregressive model, or account for it through the nonparametric circular block bootstrap, stationary block bootstrap, or subsampling. (See the Supplemental Section for more details.)
Statistical hypothesis testing
The various scientific assertions regarding the global warming hiatus are collected into four groups and then formulated as four testable statistical hypotheses. These four hypotheses are specified rigorously, in a principled statistical framework, and are given in Supplemental Sections 3.1, 3.2, 3.3 and 3.4. The Wald test is used to test slope parameters in the linear regression model in Hypotheses I and II leading to Normal or t-distribution based p-values. Moreover, p-values based on the bootstrap and subsampling are also calculated as alternatives to the Wald test whenever appropriate. When comparing two distributions, the Kolmogorov-Smirnov test is used, together with the bootstrap or subsampling, to account for temporal dependence. (See the Supplemental Section for more details.)
Observational uncertainties
It is important to recognize that the temperature data that is used in our analysis are estimates of an unobserved process and is thus subject to observational errors and the implied uncertainties. Observational uncertainties could arise due to various factors, including instrumental error, changes in the observing network configuration and observing technology, and also due to uncertainties in adjustments made to the data. The HadCRUT4 dataset allows an analysis that incorporates observational uncertainties. The single time-series used for the analysis of the HadCRUT4 data is actually derived from multiple time series which are constructed in order to reflect observational uncertainties. This analysis is provided in Supplemental Section 4.
3 Results
3.1 Hypothesis I: hiatus in temperature trend during 1998–2013
A basic assertion regarding the hiatus is that the steady increase in global surface temperature around a linear positive trend has stopped, or “paused” (Guemas et al. 2013). This sentiment is reflected in statements that “Despite a sustained production of anthropogenic greenhouse gases, the Earth’s mean near-surface temperature paused its rise during the 2000–2010 period” (Guemas et al. 2013), and that “climate skeptics have seized on the temperature trends as evidence that global warming has ground to a halt” (Tollefson 2014). These scientific claims can be turned into a precise statistical null hypothesis: the slope in the regression line of global temperature on time is zero during the hiatus period.
We use three methods with increasing levels of generality to test the above hypothesis. Specific details of the methodology are provided in Supplementary Section 3.1. First, beginning with the 1998–2013 period we fit a standard regression to the response variable global temperature on time during 1998–2013, with errors assumed to be independently and identically distributed (see Fig. 1 for the fit). A two-sided hypothesis test yields a p-value of 0.102 (a one-sided test yields a p-value of 0.051). Thus, the claim of a zero warming trend during the hiatus period cannot be rejected at the 5 % significance level. The second method fits a linear regression with autocorrelated errors that follow a parametric autoregressive model with lag 1. This model aims to directly address the year-to-year temporal dependency present in the global temperature record. Estimating the autoregression and regression parameters using the method of Cochrane and Orcutt (1949), a p-value of 0.075 is obtained for the regression slope coefficient by the bootstrap method (with one-sided p-value less than 5 %). Taking temporal dependence into account, there is now more evidence against the null hypothesis of a climate hiatus. The third method is completely nonparametric, and instead of using the parametric AR(1) approach to model the temporal dependency, a block bootstrap is used which allows for quite general forms of temporal dependence, and yields a two-sided p-value of 0.019. There is now compelling evidence to reject the claim of no warming trend during the 1998–2013 period at the 5 % significance level (and even at the 1 % level for a one-sided test). Moreover, the p-values corresponding to starting years 1999 and 2000 are 0.005 and 0.017 respectively, yielding even lower p-values - and stronger evidence against a hiatus - than when using a starting year of 1998. The sensitivity analysis highlights the fact that choosing the year 1998 had a priori favored the hiatus claim. Moreover, assuming the hiatus as the null makes it harder to conclude otherwise. Regardless, the assertion of a climate hiatus is nevertheless rejected at the 5 % level. We therefore conclude that there is “overwhelming evidence” against the claim that there has been no trend in global surface temperature over the past ≈ 15 years.
Note also that, in applying progressively more general statistical techniques, the scientific conclusions have progressively strengthened from “not significant,” to “significant at the 10 % level,” and then to “significant at the 5 % level.” It is therefore clear that naive statistical approaches can possibly lead to erroneous scientific conclusions. Methods that rely upon a strong modeling assumption of no temporal dependence, or that of a specific form, are less reliable than methods that capture dependence without assuming structural knowledge of the type of dependence.
3.2 Hypothesis II: difference in temperature trends
Otto et al. (2013) state that: “the rate of mean global warming has been lower over the past decade than previously.” This statement encompasses a second interpretation of the purported hiatus: that the hiatus represents a “slowdown” of global warming (Chen and Tung 2014), in which the rate of warming is less during the hiatus compared with the warming prior to the hiatus (Chen and Tung 2014; Otto et al. 2013; Smith 2013). This claim can be formulated as a testable statistical hypothesis, where the null hypothesis is that the regression slope before the hiatus period minus the regression slope during the hiatus period is zero or negative, versus the alternative hypothesis that this difference is positive.
We employ three different methods with increasing levels of statistical sophistication to test this hypothesis. Specific details of the methodology are provided in Supplementary Section 3.2. First, a standard regression of global temperature on time is fitted to both the 1998–2013 hiatus period and the period 1950–1997, with errors assumed to be independently and identically distributed (see Fig. 2 top left panel). The first method yields a p-value of 0.210. Thus, there is no evidence of a difference in warming trends even at the 10 % significance level. The second method accounts for the temporal dependency in the global temperature record by using a block bootstrap approach, yielding a p-value of 0.323. The evidence for a difference in trends is further weakened when temporal dependency is accounted for. The third approach uses the method of subsampling (Politis et al. 1999; Rajaratnam et al. 2014) to determine how the current 16-year trend during 1998–2013 compares against all the previous 16-year trends observed between 1950 and 1997. A p-value of 0.3939 is obtained and evidence for the hiatus is further weakened. From the plots in Fig. 2 (bottom panel), observe that during the 1950–1997 period, there are several 16-year periods with both higher and lower linear trends. Therefore the observed trend during 1998–2013 does not appear to be anomalous in a historical context.
Top panel (left) plot of the global mean land-ocean temperature index, from 1950 to 2013, with the base period of 1951–1980. The regression fits for the two time periods (1950–1997 and 1998–2013) are superimposed. Top panel (right) summary table of results for Hypothesis II Bottom panel (left) time series plot of 16-year observed trends. Bottom panel (right) histogram of 16-year observed trends
See Fig. 2 (top right panel) for a summary of results of hypothesis II. Varying the cut-off year from 1998 to either 1999 or 2000 yields p-values of 0.214 and 0.348, respectively, for the bootstrap method. Even after properly accounting for temporal dependence, and undertaking a sensitivity analysis, there is no compelling evidence to suggest that the slopes are significantly different. We therefore conclude that the rate of warming over the past ≈ 15 years is not appreciably different from the rate of warming prior to the recent period.
3.3 Hypothesis III: hiatus in the mean global temperature
Some claims have simply asserted that the annual mean global temperature has remained constant since 1998 (versus slowing of the trend in global warming). For example, Kosaka and Xie (2013) state that “Despite the continued increase in atmospheric greenhouse gas concentrations, the annual-mean global temperature has not risen in the twenty-first century”, while Tollefson (2014) states that “Average global temperatures hit a record high in 1998 – and then the warming stalled.” This claim can also be precisely formulated as a testable statistical hypothesis. The statistical model can be written as x t = μ t + ε t , where t denotes time (in years), x t is the 1998–2013 global mean temperature anomalies series, μ t is the mean parameter and ε t is the random noise component(with \(\mathbb {E}(\varepsilon _{t}) = 0, \mathbb {V}\text {ar}(\varepsilon _{t}) = \sigma ^{2}\)). The corresponding null hypothesis and alternative are given as \( H_{0}: \mathbb {E}(x_{1998}) = \mathbb {E}(x_{1998 + t}) \hspace {0.1in} \text {for} \;\; t=1,2,\cdots ,15\hspace {0.1in} \text {versus} \hspace {0.1in} H_{A}: \mathbb {E}(x_{1998}) \neq \mathbb {E}(x_{1998 + t})\).
Specific details of the methodology are provided in Supplementary Section 3.3. Hypothesis III is tested in four different ways. There are two options for determining the value of \(\mathbb {E}[x_{1998}]=\mu _{1998}\) : to directly use the observed 1998 temperature record x 1998 as a substitute for μ 1998, or to alternatively estimate μ 1998 from the regression line from the period 1950–1997. Figure 3 (top panel) illustrates this concept. As the two approaches for specifying μ 1998 yield fixed values, the inherent variability therein can be explicitly accounted for by using the bootstrap. Doing so propagates the variability in a rigorous manner. The table in Fig. 3 (bottom panel) summarizes the results of testing hypothesis III.
For Method A, when x 1998 is used as a substitute for μ 1998, the statistical test concludes that the mean has decreased during the hiatus, and thus strongly favors the hiatus claim. However, since this one single observed value is not a consistent estimate of μ 1998, the conclusion is not reliable. In Method B when μ 1998 is estimated from the 1950–1997 regression line, the null hypothesis is rejected in the opposite direction, suggesting that the mean temperature has actually increased during the hiatus period. Thus, the selection effect from choosing 1998 as the reference cut-off year has a tremendous impact on the statistical conclusion. Method C, which specifically incorporates the variability inherent in estimating μ 1998 as x 1998 leads to a different conclusion than in Method A. In particular, as soon as the variability in estimating μ 1998 to be x 1998 is incorporated, one can no longer reject the null hypothesis that the mean has remained constant - even when the high value x 1998 is used. Method D uses a value for μ 1998 which is estimated from the 1950–1997 regression and also incorporates the variability of this estimate. Here the assertion that the mean is either zero, or has decreased, is rejected.
Given the results of this nuanced analysis, we conclude that claims that the global mean temperature has not changed in recent decades are not supported by evidence. In addition, our nuanced analysis gives much needed rigor to the claim that using 1998 as a reference year amounts to “cherry picking” (Leber 2014; Stover 2014), see also Supplemental Section for detailed discussions). The results are further validated when the analysis is repeated with 1999 and 2000 as the starts of the hiatus period (see Supplemental Section 3.3). Note furthermore that since 2014 was the warmest year on record Karl et al. (2015), ignoring 2014 in our analysis can be viewed as being even more conservative, similar to using 1998 as the starting point.
3.4 Hypothesis IV: difference in year-to-year temperature changes
It is also instructive to extend the analysis above without relying on a linear model to understand trends or means. One such approach is to assess whether the distribution of year-to-year temperature changes is markedly different between the hiatus period and the prior periods. Such analysis is inherently less reliant on a statistical model of temperature on time, and hence makes fewer assumptions. The scientific assertion here is that year-to-year changes in global mean temperature during 1998–2013 are different from those during 1950–1997. Under the null hypothesis, these year-to-year changes are assumed to come from a common underlying distribution, though we do not assume that the observations of differences are independent. This framework also allows for testing of specific features of the distribution, including changes in the mean, median and variance. The empirical distribution of annual changes in the global temperature can be constructed by taking first differences: the global mean temperature during a given year is subtracted from the global mean temperature in the previous year. The first differences during 1998–2013 give rise to a 15-year times series of temperature changes. Differences in distribution (using the Kolmogorov-Smirnov (K-S) statistic), in means, medians and variances are tested using the block bootstrap and subsampling, thus taking temporal dependency fully into account. Specific details of the methodology are provided in Supplementary Section 3.4.
The results of this analysis are given in Fig. 4. Using either bootstrap or subsampling there is no evidence at the 5 % significance level to suggest that the distribution of changes during the hiatus period is different from the previous period 1950–1997. The same applies to the mean and variance of the distributions. The difference in medians is not statistically significant at the 5 % level using the block bootstrap approach, but is significant when using subsampling. However this difference in medians completely disappears when the starting year of the hiatus is changed to either 1999 or 2000, hence the result is not robust (see Table S8 in Supplemental Section 3.4). Given these results, we conclude that the distribution of annual changes in global temperature has not been different in the past 15 years than earlier in the global temperature record.
3.5 Re-analyzing recently-updated global temperature observations
We have also implemented our methodology on the recently released ERSSTv4 dataset to compare our results to the results obtained in a recent paper by Karl et al. (2015). Unlike the study by Karl et al. (2015), we do not indirectly impose Gaussianity on the temperature data (in the most general approach that we propose for each hypothesis). We also do not impose an autoregressive structure for modeling the temporal dependence. Instead we account for the temporal dependency more flexibly and non-parametrically using the circular block bootstrap and related methods. The increased sophistication allows one to have more confidence in the results’ general validity as our approach makes fewer assumptions. The end result is also compelling. First, the results in Karl et al. (2015) show a positive slope during the hiatus period (Hypothesis I) only at the 10 % significance level. Our analysis shows however that removing the arbitrary and parametric autoregressive structure on the residuals and using the block bootstrap yields significance at the 0.1 % level. The p-value stemming from our approach is less than 0.0005. The implication of the much stronger conclusion is that the warming trend observed during 1998–2014Footnote 1 arising from a model of no warming is less than 1 in 2000 (as compared to less than 1 in 20 from Karl et al. (2015)). Thus the conclusion is made stronger by a factor of 100 using the methodology we have developed.
Now consider hypothesis II which compares the warming trend during the hiatus period to that in the previous period (1950–1997). Karl et al. (2015) assert that the analysis on the corrected NOAA global temperature shows that the 90 % confidence interval for the trend in the hiatus period encompasses that of the previous period. Note that this confidence interval is based on the period 1998–2012 and is thus calculated on only 15 years of data. Since the theoretical justification of such confidence intervals is valid for large sample sizes, it is not clear how reliable the conclusion really is. On the other hand, our subsampling methodology for comparing the trends in the two periods is applicable even when the sample size in the hiatus period is small. In particular, the validity of the subsampling approach here does not rely on asymptotic arguments (i.e., increasing sample sizes) during the hiatus period. Details of the analysis are given in Tables S11 and S12 in Supplementary Section 6.
Recall that the analysis by Karl et al. (2015) requires the use of the corrected NOAA dataset to reject the claim of a hiatus. We note that our analysis rejects the hiatus claim even when using the older NOAA temperature dataset (that is, even without correcting for the data biases). The use of methodology with far fewer restrictive assumptions appears to be more robust to errors in the data. This may not be unexpected since biases in the data tend to violate basic parametric assumptions, whereas the less restrictive techniques, such as the ones we develop, can handle a variety of data generating mechanisms simply by their very non-parametric nature.
Note that, by and large, the conclusions reached by Karl et al. (2015) and our conclusions agree. However, it is important to mention that an approach based on stringent or unrealistic assumptions which agrees with our conclusions for this dataset may fail to do so on another dataset.
3.6 Summary
We summarize the overall results from all four hypothesis tests I, II, III and IV in Tables 5 and 6 in Supplementary Section 4. These two tables also analyze the sensitivity of the results to two important factors: first when the cut-off year is changed from 1998 to either 1999 or 2000; and second when the NOAA or HadCRUT4 datasets are used instead of the NASA-GISS dataset. As there are four hypotheses being tested, using a battery of rigorous test procedures, the number of hypothesis being tested are numerous. Hence the issue of multiple hypothesis testing surfaces. In particular, a certain number of these hypotheses are expected to be falsely rejected by chance alone, casting further doubt on any of the hiatus claims.
Our rigorous statistical framework yields strong evidence against the presence of a global warming hiatus. Accounting for temporal dependence and selection effects rejects - with overwhelming evidence - the hypothesis that there has been no trend in global surface temperature over the past ≈15 years. This analysis also highlights the potential for improper statistical assumptions to yield improper scientific conclusions. Our statistical framework also clearly rejects the hypothesis that the trend in global surface temperature has been smaller over the recent ≈ 15 year period than over the prior period. Further, our framework also rejects the hypothesis that there has been no change in global mean surface temperature over the recent ≈15 years, and the hypothesis that the distribution of annual changes in global surface temperature has been different in the past ≈15 years than earlier in the record. Taken together, these results clearly reject the presence of a hiatus, pause, or slowdown in global warming. In rejecting all four hiatus hypotheses, our results instead demonstrate that the evolution of global surface temperature over the past 1–2 decades is not abnormal or unexpected within the context of the long-term record of variability and change.
Without empirical evidence in support of the hiatus claims, the assumption that there has been a hiatus/pause/slow-down in global warming should be called into question. That being said, recent work investigating the geophysical causes of the recent temperature time series have provided valuable insights into the processes that create decadal-scale variability in global temperature within a long-term trend of global warming. Moreover, it is also useful that errors in data aggregation have been corrected in the recent work of Karl et al. (2015).
Notes
Though we consider the hiatus period as 1998–2013 elsewhere in the analysis, we consider the hiatus period as 1998–2014 here in order to compare directly with Karl et al. (2015)
References
Boykoff MT (2014) Media discourse on the climate slowdown. Nat Clim Chang 4:156–158. doi:10.1038/nclimate2156
Chen X, Tung KK (2014) Varying planetary heat sink led to global-warming slowdown and acceleration. Science 345(6199):897–903. doi:10.1126/science.1254937
Cochrane D, Orcutt G (1949) Application of least squares regression to relationships containing auto-correlated error terms. J Am Stat Assoc 44(245):32–61
Cowtan K, Way RG (2014) Coverage bias in the HadCRUT4 temperature series and its impact on recent temperature trends. Q J R Meteorol Soc. doi:10.1002/qj.2297
Cowtan K, Hausfather Z, Hawkins E, Jacobs P, Mann ME, Miller SK, Steinman BA, Stolpe MB, Way RG (2015) Robust comparison of climate models with observations using blended land air and ocean sea surface temperatures. Geophys Res Lett (in print) 42. doi10.1002/2015GL064888
Durack PJ, Gleckler PJ, Landerer FW, Taylor KE (2014) Quantifying underestimates of long-term upper-ocean warming. Nat Clim Chang 4:999–1005. doi:10.1038/nclimate2389
England MH, McGregor S, Spence P, Meehl GA, Timmermann A, Cai W, Gupta AS, McPhaden MJ, Purich A, Santoso A (2014) Recent intensification of wind-driven circulation in the pacific and the ongoing warming hiatus. Nat Clim Chang 4:222–227. doi:10.1038/nclimate2106
Fyfe JC, Gillett NP, Zwiers FW (2013) Overestimated global warming over the past 20 years. Nat Clim Chang 3:767–769
Guemas V, Doblas-Reyes FJ, Andreu-Burillo I, Asif M (2013) Retrospective prediction of the global warming slowdown in the past decade. Nat Clim Chang. doi:10.1038/nclimate1863
Hansen J, Ruedy R, Sato M, Lo K (2010) Global surface temperature change. Rev Geophys 48(RG4004). doi:10.1029/2010RG000345
Hawkins E, Edwards T, McNeall D (2014) Pause for thought. Nat Clim Chang 4:154–156. doi:10.1038/nclimate2150
IPCC (2013) Climate Change 2013: the physical science basis. In: Stocker TF, Qin D, Plattner G-K, Tignor M, Allen SK, Boschung J, Nauels A, Xia Y, Bex V, Midgley PM (eds) Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge
Karl TR, Arguez A, Huang B, Lawrimore JH, McMahon JR, Menne MJ, Peterson TC, Vose RS, Zhang HM (2015) Possible artifacts of data biases in the recent global surface warming hiatus. Science 348(6242):1469–1472. doi:10.1126/science.aaa5632
Kosaka Y, Xie SP (2013) Recent global-warming hiatus tied to equatorial pacific surface cooling. Nature. doi:10.1038/nature12534
Leber R (2014) We’re stuck with the global warming “hiatus” myth for years to come. New Republic. http://www.newrepublic.com/article/119212/study-atlantic-ocean-role-global-warming-hiatus
Meehl GA, Arblaster JM, Fasullo JT, Hu A, Trenberth KE (2011) Model-based evidence of deep-ocean heat uptake during surface-temperature hiatus periods. Nat Clim Chang 1:360–364. doi:10.1038/nclimate1229
Morice CP, Kennedy JJ, Rayner NA, Jones PD (2012) Quantifying uncertainties in global and regional temperature change using an ensemble of observational estimates: The HadCRUT4 data set. J Geophys Res 117:D08,101. doi:10.1029/2011JD017187
Otto A, Otto FEL, Boucher O, Church J, Hegerl G, Forster PM, Gillett NP, Gregory J, Johnson GC, Knutti R, Lewis N, Lohmann U, Marotzke J, Myhre G, Shindell D, Stevens B, Allen MR (2013) Energy budget constraints on climate response. Nat Geosci 6:415–416. doi:10.1038/ngeo1836
Politis DN, Romano JP, Wolf M (1999) Subsampling. Springer, New York
Rajaratnam B, Romano J, Tsiang M (2014) Fixed b subsampling with application to testing for a change. Technical Report, Department of Statistics, Stanford University
Santer BD, Bonfils C, Painter JF, Zelinka MD, Mears C, Solomon S, Schmidt GA, Fyfe JC, Cole JNS, Nazarenko L, Taylor KE, Wentz FJ (2014) Volcanic contribution to decadal changes in tropospheric temperature. Nat Geosci. doi:10.1038/ngeo2098
Smith D (2013) Oceanography: has global warming stalled? Nat Clim Chang 3:618–619
Stover D (2014) The global warming “hiatus”. Bulletin of the Atomic Scientists. http://thebulletin.org/global-warming-%E2%80%9Chiatus%E2%80%9D7639
Tollefson J (2014) The case of the missing heat. Nature 505:276–278
Trenberth KE, Fasullo JT (2013) An apparent hiatus in global warming? Earth’s Future 1:19–32. doi:10.1002/2013EF000165
Acknowledgments
The authors thank Ben Santer, Page Chamberlain, Francis Zwiers, and an anonymous referee for useful comments and discussions
Conflict of interests
The authors declare that they have no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Additional information
Author Contributions
B.R. and N.D. conceived the initial scope of the study; B.R. and J.R. conceived details of the overall investigation; B.R. designed the scientific framework. B.R. and J.R. translated the scientific hypothesis into statistical hypothesis and designed the statistical framework; M.T. analyzed the data and implemented the analytical tools; B.R. and J.R. developed and supervised the statistical analyses; B.R. synthesized the paper. All authors discussed the results and commented on the draft. B.R. was partially funded by the US National Science Foundation under grants DMS-CMG 1025465, AGS-1003823, DMS-1106642, DMS-CAREER-1352656 and the US Air Force Office of Scientific Research grant award FA9550-13-1-0043. J.R. was partially funded by the US National Science Foundation under grants DMS-1307973 and DMS-1007732. N.S.D. was partially funded by NSF-CAREER-0955283.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Rajaratnam, B., Romano, J., Tsiang, M. et al. Debunking the climate hiatus. Climatic Change 133, 129–140 (2015). https://doi.org/10.1007/s10584-015-1495-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-015-1495-y