Abstract
We investigate major results of the NARCCAP multiple regional climate model (RCM) experiments driven by multiple global climate models (GCMs) regarding climate change for seasonal temperature and precipitation over North America. We focus on two major questions: How do the RCM simulated climate changes differ from those of the parent GCMs and thus affect our perception of climate change over North America, and how important are the relative contributions of RCMs and GCMs to the uncertainty (variance explained) for different seasons and variables? The RCMs tend to produce stronger climate changes for precipitation: larger increases in the northern part of the domain in winter and greater decreases across a swath of the central part in summer, compared to the four GCMs driving the regional models as well as to the full set of CMIP3 GCM results. We pose some possible process-level mechanisms for the difference in intensity of change, particularly for summer. Detailed process-level studies will be necessary to establish mechanisms and credibility of these results. The GCMs explain more variance for winter temperature and the RCMs for summer temperature. The same is true for precipitation patterns. Thus, we recommend that future RCM-GCM experiments over this region include a balanced number of GCMs and RCMs.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
For several decades, the climate science and impacts science communities have sought robust estimates of changes in regional climate due to anthropogenic emissions. One common approach has been to increase the relatively coarse resolution of atmosphere–ocean global climate models (GCMs) by using various downscaling techniques. One of the most promising techniques has been embedding dynamical regional climate models (RCMs) within GCMs to obtain more regional detail and hopefully more robust detail over a particular domain of interest.
Several major international programs have explored the uncertainties in simulations of future climate on regional scales using this technique. Most noteworthy are the two completed programs for Europe, PRUDENCE (Christensen et al. 2007a) and ENSEMBLES (Christensen et al. 2010). The North American Regional Climate Change Assessment Program (NARCCAP, Mearns et al. 2009), initiated in 2006, is another such program.
The major goals of NARCCAP serve multiple communities and include establishing the credibility of climate simulations, determining the relative importance of regional and global models in quantifying the uncertainty in the responses to future forcing, developing regional climate scenarios for use by the impacts and adaptation communities, providing results for analysis by the climate research community, and providing boundary conditions for developing higher resolution climate simulations.
Two important questions posed in NARCCAP are: What do we learn about climate change over North America from the RCM experiments that is different from what we know from the parent GCMs or the suite of CMIP3 simulations, and what is the relative importance of RCMs versus GCMs in their contributions to the uncertainty of climate change produced from the full suite of simulations? We address these two questions, focusing on change in means of temperature and precipitation for two seasons (winter and summer).
2 NARCCAP experiments
The program includes two main phases: in Phase I, six RCMs use boundary conditions from the NCEP/DOE Reanalysis II for a 25-year period (1980–2004); in Phase II, the boundary conditions are provided by four GCMs for 30 years of current climate (1971–2000) and 30 years of a future climate (2041–2070) for the A2 SRES emissions scenario (Nakicenovic et al. 2000). The simulation domain of the RCMs covers northern Mexico, the lower 48 U.S. States, and most of Canada (Fig. S1). Phase I results are discussed in Mearns et al. (2012).
The six RCMs used are: the Canadian RCM (CRCM), Mesoscale Model version 5 (MM5), HadRM3 (abbreviated HRM3), RegCM3 (abbreviated RCM3), the Experimental Climate Prediction Center (ECPC) Regional Spectral Model (RSM), and the Weather Research Forecasting Model, WRF. (See Mearns et al. (2012) and the supplementary material for references.) These RCMs were chosen to provide a variety of model physics and to use models that have already performed multi-year climate change experiments. The major characteristics of the regional models are summarized on the project website.Footnote 1 Two of them (RSM and CRCM) use spectral nudging, which provides information from the host GCM not only at the boundaries, but throughout the simulation domain, thus more directly constraining these RCMs to follow the driving model.
In Phase II, we use boundary conditions from four GCMs: the NCAR-CCSM3 (Collins et al. 2006a), the Canadian Climate Centre CGCM3 (Scinocca and McFarlane 2004; Flato et al. 2000), the Hadley Centre HadCM3 (Pope et al. 2000; Gordon et al. 2000), and the GFDL AOGCM, CM2.1 (GFDL GAMDT The GFDL Global Atmospheric Model Development Team 2004). Simulations using the A2 SRES emissions scenario have been performed with all of these models as part of CMIP3,Footnote 2 and all have saved output at 6-hour intervals appropriate for driving RCMs.
2.1 Experimental design
Because limited funding precluded simulating all 24 possible nesting combinations, we adopted a balanced fractional factorial design sampling half of the 4 × 6 RCM-GCM matrix to maximize the information obtainable from the experiment. The 12 pairings are chosen so that each GCM provides boundary conditions for three different RCMs, and each RCM is nested in two different GCMs. Table 1 shows the resulting matrix of RCM-GCM pairings. This balanced design is an important difference between NARCCAP and other RCM-GCM programs.
3 Data and methods
3.1 Data
We use climate model output from two data sets. The GCM data come from the World Climate Research Program’s (WCRP’s) Coupled Model Intercomparison Project phase 3 (CMIP3); data and further information on the GCMs can be obtained from the Program for Climate Model Diagnosis and Intercomparison (PCMDI) archive.Footnote 3 Three of the four driving GCMs used in NARCCAP (GFDL, CCSM3, and CGCM3) are part of the CMIP3 data set. The simulations from the HadCM3 were specifically performed for NARCCAP, using a slightly different version of the model known as HadCM3Q0 (Collins et al. 2006b). This more recent version includes a flux adjustment and an aerosol cycle that were not in the HadCM3 version used for generating data for CMIP3. However, on a large regional scale the temperature and precipitation results of simulations with the two models are similar over North America.
The NARCCAP RCM data were all interpolated to a common 0.5 by 0.5° grid. While all model runs were performed at about the same spatial resolution, each model used a distinct map projection and thus the grids of each model are not collocated.
3.2 Methods
3.2.1 Analysis of variance (ANOVA) approach
Our approach is based on a random effects analysis of variance (ANOVA) statistical model (Kutner et al. 2005; Sain et al. 2010; see also the recent work of Li et al. 2012), which focuses on three variance components (sources of variation): the RCM, the GCM, and an error or residual term. This statistical model postulates that the total variation in the RCM output can be decomposed into these three terms, and exploits the correlations between model runs that share either an RCM or a GCM. The relative magnitude of the first two variance components is a measure of the contributions from RCM and GCM, respectively, with larger values suggesting greater importance. In contrast, large values of the residual variance component relative to the other variance components suggest either that 1) the RCM-GCM combinations are responding to the climate change scenario in very similar ways or 2) the natural variability of the climate system as represented by the RCMs is large enough to overwhelm the impact of any particular choice of RCM or GCM. Values of the variance components are estimated via maximum likelihood, with the one missing pair of RCM-GCM model runs accounted for via the properties of the joint distribution of all the model runs implied by the ANOVA statistical model.
Our approach differs from that of Déqué et al. (2007, 2012), used in the PRUDENCE and ENSEMBLES programs through the use of a formal statistical model based on the random effects ANOVA as well as the characteristics of the NARCCAP design. Further, this statistical model motivates how missing values are handled for the one incomplete RCM-GCM combination and how variance components are estimated and interpreted, as well as how we think about uncertainty through the inclusion of the error term in the statistical model. More details on the ANOVA are provided in the supplementary information (SI).
3.2.2 Climate change significance and agreement approach
Tebaldi et al. (2011) proposed a succinct and intuitive method of displaying changes and agreement among models on a map of ensemble mean climate change that distinguishes lack of signal (in the change) from lack of information due to model disagreement. First, a test of significance (t-test) of difference (future climate vs. reference period) is applied at the grid point level for the difference between each current and future simulation. If less than 50 % of the models exhibit significant difference (at the .05 level), the grid box is left as-is. Otherwise, a test for agreement in sign is applied: if 75 % or more of the models agree in sign, the grid box is cross-hatched, indicating significant agreement, and if not, it is filled with white, indicating significance but disagreement. We apply this method to three sets of model simulations: the full set of 17 models from the CMIP3 simulations that used the A2 emissions scenario, the four host GCMs (three of which are from CMIP3), and the eleven RCM sets of simulations.Footnote 4
4 Results
4.1 ANOVA
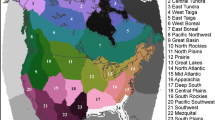
Figure 1 presents the results of the ANOVA aggregated to the Bukovsky regions (see Supplementary Material for region definitions) for summer/winter temperature/precipitation. For summer temperature (upper left panel) we see some very clear regional trends. For ocean regions, the variance of the GCMs dominates. This is to be expected, given that the ocean temperatures for the RCM simulations are inherited directly from the GCMs. The West Coast land areas are also dominated by the variance of the GCMs. However, this trend changes quite dramatically inland and over the Rocky Mountains. Here, the variance of the RCMs predominates in explaining the variability across the simulations, as expected, given the resolution of topography in the RCMs and the greater importance of regional processes such as convective precipitation and local scale soil moisture in controlling summer temperature. One exception to this pattern is the Great Lakes Region, where neither the regional nor global models predominate, but rather considerable variability is ascribed to the remainder term. This may reflect the somewhat inconsistent treatment of the Great Lakes, even for runs of the same RCM, due to various difficulties that occurred in representing the lakes or errors in lake model setups. Hence, there is complex variability across the simulations, and it is not specifically ascribable to an RCM or GCM effect.
ANOVA for summer and winter temperature (top panels) and summer and winter precipitation (bottom panels) for the Bukovsky regions. (See Supplementary Material section for region descriptions.) Bar plots represent the variance components for each of the regions. Bars are scaled by region, so the largest variance component for a particular region is shown by the largest bar, which has value equal to one. Blue denotes RCM variance, red GCM variance, and white the residual term
In winter (upper right panel) for temperature we see a combination of the dominance of the GCM effect and the remainder term. Again, the GCM effect dominates over the oceans as expected. It also dominates in the southeastern regions and most far northern regions. Given the common signal of a large amount of warming in the north seen in most model results, which is inherited from the GCMs, this partitioning of variance makes sense in these far northern areas. However, there are also other large areas where the remainder term dominates the variance. These results are difficult to interpret since they represent either small contributions from the RCM or GCM, or large contributions from the residual error that may be attributable to internal variability. ANOVA does not distinguish between these two cases. Essentially it represents areas where there may be considerable agreement in response across the GCMs and RCMs, or some form of high variability. Important contributions from the RCMs are restricted to the Northern Rockies, the Northwestern coast, and some limited contribution in the Northern Plains.
For precipitation we see similar summer/winter patterns as for temperature, with the RCMs dominating in the summer (see, e.g., Déqué et al. 2005) and the GCMs in the winter. Interestingly, the pattern of GCM dominance in winter precipitation is clearer and more common across the regions than for temperature, whereas the opposite is the case for RCM dominance.
Hence we see a general tendency for the RCMs to dominate in the summer for both temperature and precipitation and the GCMs in the winter. This is consistent with the dominance of large-scale (GCM-scale) features in winter and finer scale (mesoscale) features in summer.
4.2 Significance/agreement analysis
We focus on winter and summer precipitation (Fig. 2a, b), which present the most striking contrasts across the three ensembles of simulations. For winter precipitation (Fig. 2a) the CMIP3 models produce what is considered the standard pattern of precipitation change over North America with future forcing (Christensen et al. 2007b). In general, precipitation increases in the north and decreases in the far south in response to the northward migration of storm tracks and expansion of the subtropical high. Note, however, that the decreases lack both significance and agreement, while the increases possess both. Although most of the U.S. sees relatively small increases, they lack significance; the area of significant increase barely reaches the Northeast U.S. The four GCMs that drove the NARCCAP models (Fig. 2a, middle) display a larger area of significant increase to the north that extends well into the Northeast and Midwest, although the mean percentage increase is not very large (5–10 %). The eleven RCMs follow a pattern of significant and agreed-upon increases that looks very much like that of the four GCMs in areal extent, as opposed to the full set of CMIP3 results, but the increases are larger, mostly in the 10–20 % range. For areas with relatively high climatological precipitation, such increases under climate change could be important from an impacts point of view, especially regarding increased flooding events. Note also the larger increase in winter precipitation over the Colorado headwaters in the RCMs compared to the GCMs. Although its statistical significance is limited, this pattern is consistent with Gao et al. (2012), who found increased transient eddy moisture convergence associated with winter storms in RCMs that better resolve mountain effects due to high resolution.
Significance and agreement plots for mean change for (a) winter precipitation, and (b) summer precipitation, for three ensembles: top) the 17 CMIP3 GCM simulations; middle) the 4 GCMs used to drive the NARCCAP RCMs; and bottom) the 11 RCM simulations. The field displayed is mean percentage change in precipitation across the ensemble. Cross-hatched areas pass both the significance and agreement criteria. White areas pass significance but not agreement. See text for definitions and further explanation
For summer precipitation (Fig. 2b), the eleven RCMs (bottom panel) show a distinct deepening of the precipitation decrease (10–20 %) compared to the full set of CMIP3 model results (5–10 %) (Fig. 2b, top), as well as to the four driving GCMs (also 5–10 %) (middle panel), for a swath across the U.S. from the Northwest, across the Rockies, and east into the Appalachians. Areas of significant agreement are scattered throughout this area. This is not as evident in the CMIP3 agreement plots or in the four GCM plots. The RCMs frequently exhibit a change in sign (mostly towards drying) compared to the changes from the driving GCMs. This tendency is clearly observable in the scatter plots of change in temperature vs. precipitation for the Central Plains (Fig. 3). Note, for example, that for precipitation change, all RCMs driven by the CCSM change sign (compared to the CCSM) towards drying, as is the case for two of the RCMs driven by the CGCM3. In the case of the HadCM3, however, we see a decrease in precipitation in the GCM but a distinct increase in precipitation in the MM5 driven by HadCM3. This is the only case where the RCM produces increases in precipitation in contrast to the GCM. The largest decrease is projected by the HRM3 driven by GFDL, although in this case the decrease for the GCM is also quite large. There is also a strong linear relationship (R2 = 0.56) in this plot, where larger decreases in precipitation are associated with larger increases in temperature. Trenberth and Shea (2005) found a negative correlation between warm-season temperature and precipitation in this region in observed data, suggesting that the correlation found in the RCM results is physically consistent. This correlation is correctly reproduced by the RCMs when driven by NCEP reanalyses (Mearns et al. 2012).
Scatter plot of changes in temperature (°C) vs. changes in precipitation (%) for the Central Plains Bukovsky region (see Fig. S1 for regions definitions) for the 11 RCM and 4 GCM sets of simulations
5 Discussion
Including the RCMs markedly affects the climate change projections over North America on various spatial scales, especially in summer. Results from the RCMs provide different information than the GCMs, for both winter and summer precipitation. Most notably, the RCMs tend to agree on a deeper decrease in summer precipitation along a swath near the transition between regions that become either wetter or dryer in GCM projections. The swath also coincides with the wet/dry transition zone in the current climate, where land-atmosphere interactions (i.e., the impact of soil moisture on precipitation) are strong (Koster et al. 2004, 2006). Recent studies (Seneviratne et al. 2010; Dirmeyer et al. 2012) discuss the potential for land-atmosphere interactions to intensify under global warming, which would suggest that drying in the wet/dry transition zone could be enhanced due to stronger land-atmosphere interactions. If GCMs have less agreement than RCMs on the locations of the wet/dry transition zone (e.g., due to the models’ ability to simulate convective precipitation) or the strength of land-atmosphere coupling (Dirmeyer 2006), they may have less agreement on the drying in the future climate. Different changes in regional moisture transport and convergence between the RCMs and GCMs could be influencing the differences in this area as well. This was one potential mechanism, identified in Bukovsky and Karoly (2011) driving stronger drying in their version of WRF in a similar region versus the climate change signal in the CCSM (the same CCSM simulation downscaled in NARCCAP). This result (Bukovsky and Karoly 2011) is encouraging in providing a robust explanation for the difference in direction of change between a GCM and RCM for summer precipitation, when the influence of large scale forcing is diminished, and precipitation processes are more local in scale compared to in winter. This condition is also supported by other research (e.g., Han and Roads 2004; Pan et al. 2004) over North America, though this may not always be the case in other regions (Jones et al. 1997).
If further process-based analysis confirms that the RCM changes are credible, this would imply more serious impacts on water and agricultural resources than inferred from GCM projections, and adaptation to these changes could be much more difficult.
We also find, based on the ANOVA results, that the variance of results in summer is dominated by the RCMs, consistent with the greater role of mesoscale processes in summer climate over this region (e.g., much of warm-season precipitation in the central U.S. is produced by mesoscale convective complexes, as reviewed by Ashley et al. (2003)). These results bear some resemblance to those found in PRUDENCE and ENSEMBLES over Europe (Déqué et al. 2005, 2007, 2012), but this is the first time such an analysis has been presented over North America, and we provide a much more detailed analysis. The ANOVA results have important implications for the design of other RCM-GCM experiments, such as those of CORDEX (Giorgi et al. 2009). Including a number of different RCMs in the mix is especially important for exploring the uncertainty of climate in summer, while it is less so in winter, when the role of different GCMs dominates. This suggests that including a balanced number of RCMs and GCMs is most desirable to best explore uncertainties across the seasons. However, which RCMs and which GCMs to include needs to be carefully evaluated.
Notes
The particular simulations with HadCM3 were produced specifically for NARCCAP. See the data and methods section for details.
One set of RCM simulations (the 12th set) is not yet completed: the RSM driven by HadCM3 (a longer-term consequence of the death of the lead co-PI in charge of the simulations).
References
Ashley WS et al (2003) Distribution of mesoscale convective complex rainfall in the United States. Mon Wea Rev 131:3003–3017
Bukovsky MS, Karoly DJ (2011) A regional modeling study of climate change impacts on warm-season precipitation in the central United States. J Climate 24:1985–2002
Christensen JH et al (2007a) Evaluating the performance and utility of regional climate models: The prudence project. Clim Chang 81:1–6
Christensen JH et al (2007b) Regional climate projections. In: Solomon et al (eds) IPCC WG1, fourth assessment report, the physical science basis. Cambridge U. Press, Cambridge, pp 847–940
Christensen JH, Kjellström E, Giorgi F, Lenderink G, Rummukainen M (2010) Assigning relative weights to regional climate models: Exploring the concept. Clim Res. doi:10.3354/cr00916
Collins M et al (2006a) Towards quantifying uncertainty in transient climate change. Clim Dyn 27:127–147. doi:10.1007/s00382-006-0121-0
Collins WD et al (2006b) The community climate system model: CCSM3. J Climate 19:2122–2143
Déqué M et al (2005) Global high resolution versus limited area model climate change scenarios over Europe: Quantifying confidence level from PRUDENCE results. Clim Dyn 25:653–670
Déqué M et al (2007) An intercomparison of regional climate simulations for Europe: Assessing uncertainties in model projections. Clim Chang 81:53–70
Déqué M et al (2012) The spread amongst ENSEMBLES regional scenarios: Regional climate models, driving general circulation models, and interannual variability. Clim Dyn 38:951–964
Dirmeyer PA et al (2012) Evidence for enhanced land-atmosphere feedback in a warming climate. J Hydrometeorology 13:981–995
Dirmeyer PA (2006) The hydrologic feedback pathway for land–climate coupling. J Hydrometeor 7:857–867
Flato GM et al (2000) The Canadian centre for climate modeling and analysis global coupled model and its climate. Clim Dynam 16:451–467. doi:10.1007/s003820050339
Gao Y et al (2012) Moisture flux convergence in regional and global models: Implications for drought in the southwestern United States under climate change. Geophys Res Lett 39, L09711. doi:10.1029/2012GL051560
GFDL GAMDT (The GFDL Global Atmospheric Model Development Team) (2004) The new GFDL global atmospheric and land model AM2-LM2: Evaluation with prescribed SST simulations. J Climate 17:4641–4673
Giorgi F, Jones C, Asrar GR (2009) Addressing climate information needs at the regional level: The CORDEX framework. WMO Bull 58:175–183
Gordon C et al (2000) The simulation of SST, sea ice extents and ocean heat transports in a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 16:147–168
Han J, Roads JO (2004) US Climate sensitivity simulated with the NCEP regional spectral model. Clim Chang 62:115–154
Jones RG, Murphy JM, Noguer M, Keen AB (1997) Simulation of climate change over Europe using a nested regional-climate model. II: Comparison of driving and regional model responses to a doubling of carbon dioxide concentration. Q J R Meteorol Soc 123:265–292
Koster RD et al (2004) Regions of coupling between soil moisture and precipitation. Science 305:1138–1140
Koster RD et al (2006) GLACE: The global land–atmosphere coupling experiment. Part I: Overview. J Hydrometeor 7:590–610. doi:10.1175/JHM510.1
Kutner M, Nachtsheim C, Neter J, Li W (2005) Applied linear statistical models, 5th ed., McGraw-Hill.
Li G, Zhang X, Zwiers F, Wen QH (2012) Quantification of uncertainty in high-resolution temperature scenarios for North America. J Clim. doi:10.1175/JCLI-D-11-00217.1
Mearns LO et al. (2009) A regional climate change assessment program for North America EOS 90:311–312
Mearns LO et al (2012) The north American regional climate change assessment program: Overview of phase I results. Bull Amer Met Soc 93:1337–1362
Nakicenovic N et al (2000) Special report on emissions scenarios. Cambridge University Press, Cambridge, p 599
Pan Z et al (2004) Altered hydrologic feedback in a warming climate introduces a “warming hole”. Geophys Res Lett 31, L17109. doi:10.1029/2004GL020528
Pope VD et al (2000) The impact of new physical parameterizations in the Hadley Centre climate model: HadAM3. Clim Dyn 16:123–146
Sain S, Nychka D, Mearns LO (2010) Functional ANOVA and regional climate experiments: A statistical analysis of dynamic downscaling. Environmetrics 22:700–711. doi:10.1002/env.1068
Scinocca JF, McFarlane NA (2004) The variability of modeled tropical precipitation. J Atmos Sc 61:1993–2015
Seneviratne SI et al (2010) Investigating soil moisture-climate interactions in a changing climate: A review. Earth Sci Rev 99:125–161
Tebaldi C, Arblaster JM, Knutti R (2011) Mapping model agreement on future climate projections. Geophys Res Lett 38, L23701. doi:10.1029/2011GL049863
Trenberth KE, Shea DJ (2005) Relationships between precipitation and surface temperature. Geophys Res Lett 32, L14703. doi:10.1029/2005GL022760
Acknowledgements
This research was funded through grants from the U.S. Environmental Protection Agency—Office of Research and Development, National Oceanic and Atmospheric Administration, National Science Foundation, and U.S. Department of Energy. We also thank Don Middleton, National Center for Atmospheric Research (NCAR) and David Bader, Lawrence Livermore National Lab, for their support of data archiving. We acknowledge the modeling groups, the PCMDI, and the WCRP’s Working Group on Coupled Modeling for making available the WCRP CMIP3 multi-model dataset. Support for the CMIP3 dataset is provided by the U.S. Department of Energy Office of Science. We thank Doug Nychka, NCAR, for useful suggestions regarding analysis, Josh Thompson, NCAR, for his work on data quality control, and Zhenya Gallon for copy editing assistance. And we thank Claudia Tebaldi, Climate Central, and Julie Arblaster, Bureau of Meteorology, CSIRO for providing guidance on implementing the Tebaldi et al. method. We also thank the two anonymous reviewers for their useful comments.
Author information
Authors and Affiliations
Corresponding author
Electronic Supplementary Materials
Below is the link to the electronic supplementary material.
ESM 1
(DOC 481 kb)
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Mearns, L.O., Sain, S., Leung, L.R. et al. Climate change projections of the North American Regional Climate Change Assessment Program (NARCCAP). Climatic Change 120, 965–975 (2013). https://doi.org/10.1007/s10584-013-0831-3
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10584-013-0831-3