Skip to main content
SpringerLink
Log in

A symplectic integrator for the symmetry reduced and regularised planar 3-body problem with vanishing angular momentum

  • Original Article
  • Published:
Celestial Mechanics and Dynamical Astronomy Aims and scope Submit manuscript

Abstract

We construct an explicit reversible symplectic integrator for the planar 3-body problem with zero angular momentum. We start with a Hamiltonian of the planar 3-body problem that is globally regularised and fully symmetry reduced. This Hamiltonian is a sum of 10 polynomials each of which can be integrated exactly, and hence a symplectic integrator is constructed. The performance of the integrator is examined with three numerical examples: The figure eight, the Pythagorean orbit, and a periodic collision orbit.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9

Similar content being viewed by others

References

  • Blanes, S.: Symplectic maps for approximating polynomial Hamiltonian systems. Phys. Rev. E. Stat. Nonlinear Soft. Matter Phys. 65(5 Pt 2), 056,703 (2002)

    Article  MathSciNet  Google Scholar 

  • Blanes, S., Budd, C.J.: Adaptive geometric integrators for Hamiltonian problems with approximate scale invariance. SIAM J. Sci. Comput. 26, 1089–1113 (2005)

    Article  MathSciNet  MATH  Google Scholar 

  • Blanes, S., Iserles, A.: Explicit adaptive symplectic integrators for solving hamiltonian systems. Celest. Mech. Dyn. Astron. 114, 297–317 (2012)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Channell, P. J., Neri, F. R.: An Introduction to Symplectic Integrators, vol. 10. Fields Institute, Communications, pp. 45–58. American Mathematical Society (1996)

  • Chenciner, A., Montgomery, R.: A remarkable periodic solution of the three body problem in the case of equal masses. Ann. Math. 152, 881–901 (2000)

    Article  MathSciNet  MATH  Google Scholar 

  • Gjaja, I.: Monomial factorization of symplectic maps. Part. Accel. 43(3), 133–144 (1994)

    MathSciNet  Google Scholar 

  • Gruntz, D., Waldvogel, J.: Orbits in the planar three-body problem. In: Gander, W., Hřebíček, J. (eds.) Solving Problems in Scientific Computing Using Maple and Matlab, Chap. 4, 4th edn, pp. 51–72. Springer, Berlin (2004)

    Chapter  Google Scholar 

  • Hairer, E., Lubich, C., Wanner, G.: Geometric Numerical Integration. Springer, Berlin (2002)

    Book  MATH  Google Scholar 

  • Heggie, D.: A global regularisation of the gravitationaln-body problem. Celest. Mech. 10(2), 217–241 (1974)

    Google Scholar 

  • Ito, T., Tanikawa, K.: Trends in 20th century celestial mechanics. Publ. Natl. Astron. Obs. Jpn. 9, 55–112 (2007)

    ADS  Google Scholar 

  • Kustaanheimo, P., Stiefel, E.: Perturbation theory of kepler motion based on spinor regularization. J. Math. Bd. 218, 27 (1965)

    Google Scholar 

  • Leimkuhler, B., Reich, S.: Simulating Hamiltonian Dynamics. Cambridge University Press, Cambridge (2004)

    MATH  Google Scholar 

  • Lemaître C (1964) The three body problem. Technical report, NASA CR-110. http://ntrs.nasa.gov/

  • McLachlan, R.I., Quispel, G.R.W.: Splitting methods. Acta Numer. 11, 341–434 (2002)

    Article  MathSciNet  MATH  Google Scholar 

  • Mikkola, S.: Practical symplectic methods with time transformation for the few-body problem. Celest. Mech. Dyn. Astron. 67, 145–165 (1997)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Moeckel, R., Montgomery, R.: Symmetric regularization, reduction and blow-up of the planar three-body problem (2012, preprint). arXiv:12020972

  • Moore, C.: Braids in classical dynamics. Phys. Rev. Lett. 70, 3675–3679 (1993)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Preto, M., Tremaine, S.: A class of symplectic integrators with adaptive time step for separable hamiltonian systems. Astron. J. 118, 2532–2541 (1999)

    Article  ADS  Google Scholar 

  • Quispel, G.R.W., Mclachlan, R.: Explicit geometric integration of polynomial vector fields. BIT Numer. Math. 44, 515–538 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  • Shi, J., Yan, Y.T.: Explicitly integrable polynomial hamiltonians and evaluation of lie transformations. Phys. Rev. E 48(5), 3943 (1993)

    Article  MathSciNet  ADS  Google Scholar 

  • Simó, C.: Periodic orbits of the planar N-body problem with equal masses and all bodies on the same path. In: Steves, B.A., Maciejewski, A.J. (eds.) pp. 265–284. The Restless Universe (2001)

  • Simó, C.: Dynamical properties of the figure eight solution of the three-body problem. In: Chenciner, A., Cushman, R., Robinson, C., Xia, Z.J. (eds.) Celestial Mechanics, Dedicated to Donald Saari for his 60th Birthday, Vol. 1, pp. 209–228 (2002)

  • Szebehely, V., Peters, C.F.: Complete solution of a general problem of three bodies. Astron. J. 72, 876–883 (1967). doi:10.1086/110355

    Article  ADS  Google Scholar 

  • Waldvogel, J.: A new regularization of the planar problem of three bodies. Celest. Mech. 6, 221–231 (1972). doi:10.1007/BF01227784

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Waldvogel, J.: Symmetric and regularized coordinates on the plane triple collision manifold. Celest. Mech. 28, 69–82 (1982)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  • Yoshida, H.: Construction of higher order symplectic integrators. Phys. Lett. A 150, 262–268 (1990)

    Article  MathSciNet  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. School of Mathematics and Statistics, University of Sydney, Sydney, NSW, 2006, Australia

    Danya Rose & Holger R. Dullin

Authors
  1. Danya Rose
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Holger R. Dullin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Danya Rose.

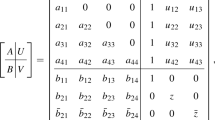
Appendix: Integrator stages

Appendix: Integrator stages

Section 3.1 described how to integrate a monomial Hamiltonian, and Sect. 3.2 described the splitting of Eq. (2) into a minimal number of solvable parts and those solutions. Here we use those solutions to build an explicit first order symplectic composition method for (2).

Let the timestep be \(\varDelta \tau \), let \(\mu _j = (m_k + m_l)\), let the values of the system before and after one timestep respectively be \(\varvec{z}_0 = (\alpha _{1,0},\dots ,\pi _{3,0})^T\) and \(\varvec{z}_1 = (\alpha _{1,1},\ldots ,\pi _{3,1})^T\) and intermediate steps be \(\varvec{\xi }_i = (\alpha _{1,.i-1},\ldots ,\pi _{3,.i-1})^T\). Now

$$\begin{aligned} \varvec{\xi }_1&= \left( \begin{array}{c} \alpha _{1,0} \\ \alpha _{2,0} \\ \alpha _{3,0} \\ \pi _{1,0} + 2 \alpha _{1,0} \left( \left( 2\alpha _{1,0}^2 + a_{1,0}\right) \left( h a_{1,0} + M_1\right) + m_1 \alpha _{1,0} \mu _1 a_{1,0}\right) \varDelta \tau \\ \pi _{2,0} + 2 \alpha _{2,0} \left( \left( 2\alpha _{2,0}^2 + a_{2,0}\right) \left( h a_{2,0} + M_2\right) + m_2 \alpha _{2,0} \mu _2 a_{2,0}\right) \varDelta \tau \\ \pi _{3,0} + 2 \alpha _{3,0} \left( \left( 2\alpha _{3,0}^2 + a_{3,0}\right) \left( h a_{3,0} + M_3\right) + m_3 \alpha _{3,0} \mu _3 a_{3,0}\right) \varDelta \tau \end{array}\right) \\ \varvec{\xi }_2&= \left( \begin{array}{c} \alpha _{1,.1}\ \exp \left( \frac{1}{4} \left( N_2 \alpha _{2,.1}^2 + N_3 \alpha _{3,.1}^2\right) \alpha _{1,.1}\ \pi _{1,.1}\ \varDelta \tau \right) \\ \alpha _{2,.1} \\ \alpha _{3,.1} \\ \pi _{1,.1}\ \exp \left( -\frac{1}{4} \left( N_2 \alpha _{2,.1}^2 + N_3 \alpha _{3,.1}^2\right) \alpha _{1,.1}\ \pi _{1,.1}\ \varDelta \tau \right) \\ \pi _{2,.1} - \frac{1}{4}\ N_2\ \alpha _{1,.1}^2\ \pi _{1,.1}^2\ \alpha _{2,.1} \varDelta \tau \\ \pi _{3,.1} - \frac{1}{4}\ N_3\ \alpha _{1,.1}^2\ \pi _{1,.1}^2\ \alpha _{3,.1} \varDelta \tau \end{array}\right) \\ \varvec{\xi }_3&= \left( \begin{array}{c} \alpha _{1,.2} \\ \alpha _{2,.2}\ \exp \left( \frac{1}{4} \left( N_3 \alpha _{3,.2}^2 + N_1 \alpha _{1,.2}^2\right) \alpha _{2,.2}\ \pi _{2,.2}\ \varDelta \tau \right) \\ \alpha _{3,.2} \\ \pi _{1,.2} - \frac{1}{4}\ N_1\ \alpha _{2,.2}^2\ \pi _{2,.2}^2\ \alpha _{1,.2} \varDelta \tau \\ \pi _{2,.2}\ \exp \left( -\frac{1}{4} \left( N_3 \alpha _{3,.2}^2 + N_1 \alpha _{1,.2}^2\right) \alpha _{2,.2}\ \pi _{2,.2}\ \varDelta \tau \right) \\ \pi _{3,.2} - \frac{1}{4}\ N_3\ \alpha _{2,.2}^2\ \pi _{2,.2}^2\ \alpha _{3,.2} \varDelta \tau \end{array}\right) \\ \varvec{\xi }_4&= \left( \begin{array}{c} \alpha _{1,.3} \\ \alpha _{2,.3} \\ \alpha _{3,.3}\ \exp \left( \frac{1}{4} \left( N_1 \alpha _{1,.3}^2 + N_2 \alpha _{2,.3}^2\right) \alpha _{3,.3}\ \pi _{3,.3}\ \varDelta \tau \right) \\ \pi _{1,.3} - \frac{1}{4}\ N_1\ \alpha _{3,.3}^2\ \pi _{3,.3}^2\ \alpha _{1,.3} \varDelta \tau \\ \pi _{2,.3} - \frac{1}{4}\ N_2\ \alpha _{3,.3}^2\ \pi _{3,.3}^2\ \alpha _{2,.3} \varDelta \tau \\ \pi _{3,.3}\ \exp \left( -\frac{1}{4} \left( N_1 \alpha _{1,.3}^2 + N_2 \alpha _{2,.3}^2\right) \alpha _{3,.3}\ \pi _{3,.3}\ \varDelta \tau \right) \end{array}\right) \end{aligned}$$
$$\begin{aligned} \varvec{\xi }_5&= \left( \begin{array}{c} \alpha _{1,.4} + \pi _{1,.4} \left( \frac{1}{4} \left( N_2 \alpha _{2,.4}^4 + N_3 \alpha _{3,.4}^4\right) + \frac{1}{2 m_1}\alpha _{2,.4}^2 \alpha _{3,.4}^2\right) \varDelta \tau \\ \alpha _{2,.4} \\ \alpha _{3,.4} \\ \pi _{1,.4} \\ \pi _{2,.4} + \frac{1}{2} \pi _{1,.4}^2 \left( N_2 \alpha _{2,.4}^3 + \frac{1}{m_1} \alpha _{2,.4} \alpha _{3,.4}^2\right) \varDelta \tau \\ \pi _{3,.4} + \frac{1}{2} \pi _{1,.4}^2 \left( N_3 \alpha _{3,.4}^3 + \frac{1}{m_1} \alpha _{3,.4} \alpha _{2,.4}^2\right) \varDelta \tau \end{array}\right) \\ \varvec{\xi }_6&= \left( \begin{array}{c} \alpha _{1,.5} \\ \alpha _{2,.5} + \pi _{2,.5} \left( \frac{1}{4} \left( N_3 \alpha _{3,.5}^4 + N_1 \alpha _{1,.5}^4\right) + \frac{1}{2 m_2}\alpha _{3,.5}^2 \alpha _{1,.5}^2\right) \varDelta \tau \\ \alpha _{3,.5} \\ \pi _{1,.5} + \frac{1}{2} \pi _{2,.5}^2 \left( N_1 \alpha _{1,.5}^3 + \frac{1}{m_2} \alpha _{1,.5} \alpha _{3,.5}^2\right) \varDelta \tau \\ \pi _{2,.5} \\ \pi _{3,.5} + \frac{1}{2} \pi _{2,.5}^2 \left( N_3 \alpha _{3,.5}^3 + \frac{1}{m_2} \alpha _{3,.5} \alpha _{1,.5}^2\right) \varDelta \tau \end{array}\right) \\ \varvec{\xi }_7&= \left( \begin{array}{c} \alpha _{1,.6} \\ \alpha _{2,.6} \\ \alpha _{3,.6} + \pi _{3,.6} \left( \frac{1}{4} \left( N_1 \alpha _{1,.6}^4 + N_2 \alpha _{2,.6}^4\right) + \frac{1}{2 m_3}\alpha _{1,.6}^2 \alpha _{2,.6}^2\right) \varDelta \tau \\ \pi _{1,.6} + \frac{1}{2} \pi _{3,.6}^2 \left( N_1 \alpha _{1,.6}^3 + \frac{1}{m_3} \alpha _{1,.6} \alpha _{2,.6}^2\right) \varDelta \tau \\ \pi _{2,.6} + \frac{1}{2} \pi _{3,.5}^2 \left( N_2 \alpha _{2,.5}^3 + \frac{1}{m_3} \alpha _{2,.5} \alpha _{1,.5}^2\right) \varDelta \tau \\ \pi _{3,.6} \end{array}\right) \\ \varvec{\xi }_8&= \left( \begin{array}{c} \alpha _{1,.7} \left( 1 + \frac{1}{2} \left( \frac{1}{m_3} \alpha _{2,.7} \pi _{2,.7} + \frac{1}{m_2} \alpha _{3,.7} \pi _{3,.7}\right) \alpha _{1,.7}^2 \varDelta \tau \right) ^{-\frac{1}{2}} \\ \alpha _{2,.7} \exp \left( -\frac{1}{4 m_3}\alpha _{1,.7}^3 \pi _{1,.7} \varDelta \tau \right) \\ \alpha _{3,.7} \exp \left( -\frac{1}{4 m_2}\alpha _{1,.7}^3 \pi _{1,.7} \varDelta \tau \right) \\ \pi _{1,.7} \left( 1 + \frac{1}{2} \left( \frac{1}{m_3} \alpha _{2,.7} \pi _{2,.7} + \frac{1}{m_2} \alpha _{3,.7} \pi _{3,.7}\right) \alpha _{1,.7}^2 \varDelta \tau \right) ^{\frac{3}{2}} \\ \pi _{2,.7} \exp \left( \frac{1}{4 m_3}\alpha _{1,.7}^3 \pi _{1,.7} \varDelta \tau \right) \\ \pi _{3,.7} \exp \left( \frac{1}{4 m_2}\alpha _{1,.7}^3 \pi _{1,.7} \varDelta \tau \right) \end{array}\right) \end{aligned}$$
$$\begin{aligned} \varvec{\xi }_9&= \left( \begin{array}{c} \alpha _{1,.8} \exp \left( -\frac{1}{4 m_3}\alpha _{2,.8}^3 \pi _{2,.8} \varDelta \tau \right) \\ \alpha _{2,.8} \left( 1 + \frac{1}{2} \left( \frac{1}{m_1} \alpha _{3,.8} \pi _{3,.8} + \frac{1}{m_3} \alpha _{1,.8} \pi _{1,.8}\right) \alpha _{2,.8}^2 \varDelta \tau \right) ^{-\frac{1}{2}} \\ \alpha _{3,.8} \exp \left( -\frac{1}{4 m_1}\alpha _{2,.8}^3 \pi _{2,.8} \varDelta \tau \right) \\ \pi _{1,.8} \exp \left( \frac{1}{4 m_3}\alpha _{2,.8}^3 \pi _{2,.8} \varDelta \tau \right) \\ \pi _{2,.8} \left( 1 + \frac{1}{2} \left( \frac{1}{m_1} \alpha _{3,.8} \pi _{3,.8} + \frac{1}{m_3} \alpha _{1,.8} \pi _{1,.8}\right) \alpha _{2,.8}^2 \varDelta \tau \right) ^{\frac{3}{2}} \\ \pi _{3,.8} \exp \left( \frac{1}{4 m_1}\alpha _{2,.8}^3 \pi _{2,.8} \varDelta \tau \right) \end{array}\right) \\ \varvec{\xi }_{10}&= \left( \begin{array}{c} \alpha _{1,.9} \exp \left( -\frac{1}{4 m_2}\alpha _{3,.9}^3 \pi _{3,.9} \varDelta \tau \right) \\ \alpha _{2,.9} \exp \left( -\frac{1}{4 m_1}\alpha _{3,.9}^3 \pi _{3,.9} \varDelta \tau \right) \\ \alpha _{3,.9} \left( 1 + \frac{1}{2} \left( \frac{1}{m_2} \alpha _{1,.9} \pi _{1,.9} + \frac{1}{m_1} \alpha _{2,.9} \pi _{2,.9}\right) \alpha _{3,.9}^2 \varDelta \tau \right) ^{-\frac{1}{2}} \\ \pi _{1,.9} \exp \left( \frac{1}{4 m_2}\alpha _{3,.9}^3 \pi _{3,.9} \varDelta \tau \right) \\ \pi _{2,.9} \exp \left( \frac{1}{4 m_1}\alpha _{3,.9}^3 \pi _{3,.9} \varDelta \tau \right) \\ \pi _{3,.9} \left( 1 + \frac{1}{2} \left( \frac{1}{m_2} \alpha _{1,.9} \pi _{1,.9} + \frac{1}{m_1} \alpha _{2,.9} \pi _{2,.9}\right) \alpha _{3,.9}^2 \varDelta \tau \right) ^{\frac{3}{2}} \end{array}\right) = \varvec{z}_1. \end{aligned}$$

Rights and permissions

Reprints and permissions

About this article

Cite this article

Rose, D., Dullin, H.R. A symplectic integrator for the symmetry reduced and regularised planar 3-body problem with vanishing angular momentum. Celest Mech Dyn Astr 117, 169–185 (2013). https://doi.org/10.1007/s10569-013-9503-x

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s10569-013-9503-x

Keywords

Search

Navigation