Abstract
Although it is known that forestry mitigates carbon emissions to some degree, there is still a need to investigate the extent to which changes in forest management regimes affect the carbon cycle. In a climate-change scenario, forest management schemes must be optimized to maximize product supply and minimize environmental impacts. It is difficult to predict the mitigating effects of different silvicultural regimes because of differences in the growth characteristics of each species, destination of products, and industrial efficiencies. The objective of the present study was to use a modeling approach to evaluate the effects of different management regimes for fast growing species in southern temperate Europe in relation to mitigating climate change. A comprehensive study was carried out considering the C sink effect in biomass, soil and wood products, the substitutive effect of bioenergy, and particular conditions of the forest industry in southern Europe. The mechanistic CO2Fix model was parameterized for three species used in fast growing plantations in southern Europe: Eucalyptus globulus, Eucalyptus nitens, and Pinus radiata. Data from 120 plots covering the complete age range observed for each species were used to calculate changes in C stocks in aboveground biomass and organic and mineral soil and to validate the parameterized model for these conditions. Additional information about the efficiency of forest industry processes in the region was also considered. A strong bias in soil organic carbon estimation was observed and attributed to overestimations in the decomposition rates of soil compartments. Slight bias was also observed in the carbon biomass estimation when forest-specific yield models were used to simulate afforestation over former pastureland. As regards the model sensitivity, the Yasso model was strongly robust to turnover of leaves, roots, and branches. The chip wood production alternative yielded higher carbon stock in biomass and products, as well as in bioenergy substitution effect, than the sawn wood production alternative. Nevertheless, the sawn wood alternative was the most effective as regards the C stock in the soil. Site index had an important effect for all species, alternatives, and compartments, and mitigating effects increased with site index. Harvesting of clearcutting and thinning slash for bioenergy use led to a slight decrease in the soil carbon equilibrium but significantly increased the mitigation effect through bioenergy use.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
The United Nations Framework Convention on Climate Change (UNFCCC) has recognized the importance of forestry plantations for mitigating greenhouse gases, as well as the need to monitor, preserve, and enhance terrestrial carbon stocks. Forest management in Europe generates considerable reductions in carbon emissions (Groen et al. 2006), and Atlantic and central/mid European mountain sites have the largest carbon sequestration potential in Europe (Nabuurs and Schelhaas 2002).
The Kyoto Protocol (UNFCCC 1997) recognizes two main alternatives for emissions compensation in the Land Use, Land Use Change and Forestry (LULUCF) sector for Annex I countries, depending on whether actions took place in their own territory (Art. 3.3, 3.4, and 6) or in other non-Annex I countries (Art. 12). For actions inside their own borders, the Kyoto Protocol (KP) allows countries included in Annex I the following activities for compliance with the KP (UNFCCC 1997, UNFCCC 2001): compensation of greenhouse gas (GHGs) emissions through removal from direct human-induced land-use change and forestry activities, limited to afforestation, reforestation and deforestation since 1990 (Art. 3.3), and forest management activities (Art. 3.4).
The mitigation effects of forests can be achieved by maintaining or increasing the C stocks in the existing pools (biomass, soil, and dead wood, sequestration) or potential pools (wood products and bioenergy substitution), being these two alternatives of particular importance in plantations (Böttcher and Lindner 2010). Options for enhancement and maintenance of carbon sequestration are reducing deforestation, expanding forest areas, increasing the carbon stock in existing forests (including soils), increasing the use and lifespan of wood products, and using wood products as biofuels for substituting fossil fuels (Kauppi et al. 2001; Nabuurs and Schelhaas 2002).
In this sense, large areas of agricultural land have been transformed to forest plantations in Spain since the implementation of EEC directive 2080/92 (EU 1992), which laid down a grant scheme for promoting reconversion of agricultural land to forestland. Although the effects on the C stock change in the system have been already studied (Pérez-Cruzado et al. 2012), the effects of forest management on the C stock in this particular system are still not clear. Appropriate management of a forest system should guarantee maintenance of or an increase in C balance, independently of the management objectives, which sometimes focus on enhancement of carbon in forest biomass, although this has an impact on soils and wood products (Karjalainen 1996). Proper management may be a crucial factor regarding soil, which can act as a source of greenhouse gases (CO2, CH4 and N2O) or a sink (CO2 and CH4), depending on land use and land management (Lal 1999).
The chain of forest activities related to afforestation covers many different silvicultural practices, which aim to produce specific products used by the forest industry, or for bioenergy purposes. Forestry in Atlantic southwestern Europe is dominated by the use of fast growing species, which can be either introduced species Eucalyptus globulus (Labill), Eucalyptus nitens (Dean and Maiden) Maiden, and Pinus radiata (D. Don) or native species (Pinus pinaster). Moreover, the forest industry relies strongly on timber transformation, and any study of the mitigating effects of forest plantations should consider the specific transformation processes. There is a long history of forestry in northern Spain, which currently covers the range of primary transformation activities, to produce wood pulp, chipboard, sawn wood, and plywood. These industries are also characterized by a high level of integration, whereby the industrial residues produced by one line of transformation are usually used by other industries with lower requirements for raw material. The use of each lot of wood depends upon the timber assortment and species. Production of bleached eucalypt pulp (BEP) is important as regards E. globulus and, to a lesser extent, E. nitens. There is no diameter threshold limit for pulp, but bark separation becomes more difficult when the small-end diameter is less than 7 cm over bark. The board industry (MDF, HDF, or particle board) acts as a subsidiary of the pulp industry, consuming many different species of wood of small diameter.
The sawn wood industry mainly consumes P. radiata timber, with increasing interest in both E. globulus and E. nitens (Nutto and Touza Vázquez 2004). The size limitation for this industry is 15 cm in small end for pines, and although this has not been defined for either Eucalyptus species, a threshold limit of 30 cm could be considered. Waste and sawdust from sawing are used by the board industry. The plywood industry requires the largest small-end diameters, and debarking is required.
An important share of the energy demands of wood-based industries is met by combusting the residual biomass generated during timber processing (mainly tree bark and sawdust). However, harvesting of thinning slash is increasingly implemented in management schemes. Although the proportion of slash that machinery is able to harvest is between 75 and 85% (Tolosana 2009), leaving 50% slash in place is recommended for soil protection and nutritional purposes (Balboa-Murias et al. 2006; Merino et al. 2005), but the effects on global C mitigation are still under investigation.
Regarding C estimation, it is logistically impractical to sample the many sites, soil types, management regimes, landscapes, and climatic regimes with sufficient intensity to quantify the potential of SOC sequestration (Lemma et al. 2007). Model development is therefore an essential tool for evaluating the mitigating effects of forest systems. In particular, soil models are valuable tools for understanding the mechanisms of SOC build-up (Liski et al. 2005; Palosuo et al. 2008). The development of accurate models for predicting forest C evolution can therefore provide valuable information for scientists and policy makers. Simulating forest growth with very detailed process-based models can only be executed at a limited number of sites because of the need for initialization data and computing capacity (Karjalainen et al. 2002), and models must therefore be as simple as possible. In order to scale up to higher land levels (regional or national), models should represent the average growth conditions for the species considered and the selected climate zone (Karjalainen et al. 2002), which is difficult with very simple models.
The objectives of this study were (1) to parameterize the CO2Fix model for plantations of E. globulus, E. nitens, and P. radiata established over former agricultural land, (2) to validate the results with a network of plots in which biomass and soil carbon density are measured directly, (3) to evaluate the model sensitivity to several key parameters, and (4) to establish the baseline of the standard management alternatives for each species and to evaluate the effect of silviculture on the mitigating effect of these plantations.
Materials and methods
Site description
The study was carried out in the temperate-climate zone of northern Spain. The average annual temperature is between 11.5 and 13.3°C; precipitation is between 1,213 and 1,488 mm, with 411–808 mm distributed in the growing season (Table 1). The soil humidity and temperature regimes are Udic (mean period with partial drought, 1 month) and Mesic (mean frost-free period, 10 months), respectively. The soils were developed from granitic rocks, schist, and shale and classified as Humic or Distric Cambisols and Alumi-humic Umbrisols (IUSS Working Group WRB 2006). The soil has a loam or sandy loam texture and is well drained. Other site characteristics regarding soil organic carbon (SOC), litter accumulation, and species productivity are shown in Table 2. The ranges of plot ages cover the usual rotation lengths applied to these plantations (1–23 years for E. globulus, 2–18 years for E. nitens and 2–40 years for P. radiata).
The CO2Fix model
The CO2Fix model was used (Mohren and Goldewijk 1990; Mohren et al. 1999) to quantify the C balance based on growth rates and allometry. Version 3.1 of the model (Masera et al. 2003; Schelhaas et al. 2004) enables quantification of the C stocks and fluxes with a full carbon accounting approach (Nabuurs et al. 2002). This model is divided into six modules: biomass, soil, products, bioenergy, financial, and carbon accounting. Model profitability for even- and uneven-aged forest stands has already been demonstrated, but special parameterizations have also been carried out, that is, for non-forest systems, coppice, and catastrophic events (Groen et al. 2006; Schelhaas et al. 2004). Multi-cohort systems can also be simulated with this model.
The biomass module drives C changes in the other compartments. Live biomass growth must be provided in the model for the following fractions: stem, branches, leaves, and roots. The model considers tree senescence mortality, as well as reductions in the biomass pool due to logging. Soil module inputs include biomass turnover and logging residues, and soil dynamics are managed by the Yasso model (Liski et al. 2005). The latter model considers three litter compartments and five decomposition compartments, in which organic matter transfer from fresh to more humified compartments depends on the chemical characteristics and on temperature and water availability. The CO2Fix version used in this study incorporates an energy substitution module, which calculates the C-equivalent greenhouse gas flow differences between biomass-generated energy and energy derived from alternative fossil fuel. For more details about version 3.1 of the CO2Fix model, see Masera et al. (2003) and Schelhaas et al. (2004).
Biomass module parameterization
The biomass module was parameterized as a function of stand age by using the yield models developed by Pérez-Cruzado et al. (2011a) for E. globulus and E. nitens. Since there were two forest stand–specific models available for P. radiata (Castedo-Dorado et al. 2007, 2009), the suitability of both was tested. These models enable estimation of stem wood yield at the stand level in terms of current annual increment over bark (CAI, m3 ha−1 year−1). Regional site quality models were used to transform dominant height to age for each species: for the single stem rotation of E. globulus (Fernández López 1982), for E. nitens (Pérez-Cruzado 2009), and for P. radiata (Diéguez-Aranda et al. 2005). No mortality is included in the corresponding tab of the CO2Fix model, since this was captured in the yield models.
The suitability of yield models for biomass prediction was guaranteed for E. globulus and E. nitens, as the plots used for result validation were also considered in developing the growth models (Pérez-Cruzado et al. 2011a), whereas two forest-specific models were used to construct P. radiata yield tables. Results obtained from the static (Castedo-Dorado et al. 2009) and dynamic (Castedo-Dorado et al. 2007) models available for P. radiata in the region were compared with the present results, with regional adjustments with 40 plots used for model validation, all established over former agricultural land. For this, equations for quadratic mean diameter (d g , cm) prediction from dominant height (H 0, m) and tree density (N, stems ha−1) (1), and for stand volume over bark estimation (V, m3 ha−1) (2) were fitted for 40 P. radiata plots established on former pastureland. The site characteristics of these data are shown in Tables 1 and 2. Equations 1 and 2 were fitted simultaneously by the MODEL procedure of the SAS/ETS® system (SAS Institute Inc 2004), and heteroscedasticity was corrected as below.
Wood density over bark (ρ, kg m−3) was determined considering the dry weight of wood and bark estimated from biomass equations at tree level (Brañas et al. 2000; Pérez-Cruzado and Rodríguez Soalleiro 2011; Merino et al. (2005) for E. globulus, E. nitens, and P. radiata, respectively), and stem volume over bark estimated from regional taper functions (Sánchez et al. 2004; Pérez-Cruzado 2009; Castedo-Dorado et al. 2007 for E. globulus, E. nitens, and P. radiata, respectively), both estimated until 7 cm over small end bark.
Since there were no local models for root biomass estimation for the Eucalyptus species, the O’Grady et al. (2005) and the Resh et al. (2003) models were used for E. globulus and E. nitens, respectively. With the exception of leaves and roots, the other biomass fractions considered in the CO2Fix model are not the same as those used in the tree-level biomass equations The average carbon contents (C, %) were determined for branches and stem considering the proportion of each fraction included in the biomass equations. The proportion of each biomass fraction was calculated from biomass equations, and a weighted average was calculated for C, for each tree measured in all plots. The average values of C in each CO2Fix biomass fraction were estimated from carbon concentrations published for each biomass fraction considered (Merino et al. 2005; Pérez-Cruzado et al. 2011a; Balboa-Murias et al. 2006 for E. globulus, E. nitens, and P. radiata, respectively). Average values for ρ and C for each species considered are shown in Table 3.
Additional models were developed in this study for determination of allocation coefficients, and thus, models for stem biomass (W s , Mg ha−1) defined as wood plus bark in the stem until 7 cm in small end, branch biomass (W b , Mg ha−1), leaf biomass (W l , Mg ha−1), and root biomass (W r , Mg ha−1) were fitted for each species considered. The same database of plots as described in Pérez-Cruzado et al. (2011a) for E. globulus and E. nitens was used for stand-level model construction, and the plots measured in this study and the biomass equations at tree level developed by Merino et al. (2005) for P. radiata. The models took the form described in Eqs. 3–6 and enabled measurement of the biomass allocation in each biomass compartment. Values obtained for each simulation and age were set to 1, to determine the allocation factor for each compartment relative to stem biomass.
The equations were fitted by use of the MODEL procedure of the SAS/ETS® system (SAS Institute Inc 2004). Because of the existence of correlation between error components of the independent variables and dependent variables, the full information maximum likelihood method (FIML) was applied in the fitting process. Equations for each species were fitted simultaneously by the seemingly unrelated regressions method (SUR) to guarantee the additivity of the system (Parresol 2001). The MODEL procedure of SAS was applied to obtain the SUR estimates, considering the parameters obtained in a previous individual fitting as initializers. Lack of homogeneity in the variance was corrected as reported by Pérez-Cruzado and Rodríguez Soalleiro (2011).
Soil module parameterization
The supply of dead organic matter to the soil is the key factor in soil organic matter evolution, and accurate estimation is required for realistic simulations. Since litterfall and root turnover were not evaluated in the field, leaf, branch, and root turnover were determined indirectly.
Leaf litterfall is a crucial parameter for eco-physiological growth models, that is, 3-PG (Landsberg and Waring 1997), where an accurate value of this parameter enables matching the observed yield in permanent plots. For leaf turnover (LT), the parameters fitted for the 3-PG model for each species were considered: Sands and Landsberg (2002) for E. globulus, Pérez-Cruzado et al. (2011b) for E. nitens, and Rodríguez et al. (2002a) for P. radiata. The 3-PG model considers two different LT depending on tree age, but although the initial litterfall is significantly lower, it is time limited relative to the maximum value, which tends to be asymptotic and dominates throughout the rotation (Sands and Landsberg 2002). The values of LT considered (Table 3) are consistent with the observed average leaf lifespan for each species, and with reported litterfall for P. radiata (Santalla et al. 2011) and E. globulus (Alvarez et al. 2008) in the region.
Branch turnover (BT) was estimated considering the changes in tree and crown dimensions over time. It was considered that all branches have fallen when the living crown basis (h cb ) increases in the stem between time t 1 and t 2 (Fig. 1). For the species in which dead branches in the stem (w db ) are significant [e.g., E. nitens (Pérez-Cruzado and Rodríguez Soalleiro 2011)], the proportional part of this biomass that is held in the stem at time t 2 was considered; in other cases, A must be set to 0. Equation 7 was used to estimate the BT considering time intervals of 1 year and using the yield tables reported in biomass module parameterization section. Average tree dimensions were estimated for each time interval, where \( \bar{d} \) was estimated from d g using the equations developed by Pérez-Cruzado et al. (2011a) for E. globulus and E. nitens, and by Castedo-Dorado et al. (2007) for P. radiata. Total height was estimated from generalized height–diameter relationships for each species, and living crown basis (h cb ) was estimated from the equations of Nutto and Touza Vázquez (2004) for E. globulus, our own model for E. nitens (data not shown), and that of Crecente-Campo (2008) for P. radiata. For BT, an average value was obtained from \( \bar{d} \) = 10 cm to \( \bar{d} \)=50 cm; values for BT for each species are shown in Table 3.
Root turnover (RT) is not easy to determine, even when a specific experimental design is followed, and results vary greatly depending on the methodology used (Jourdan et al. 2008). The turnover rate of total root systems depends on the turnover rate of each root size. It is known that turnover of fine roots is faster than that of thicker roots, and therefore, the proportion of root sizes must be considered to obtain a global average value. Moreover, the proportion of different sized roots changes over time, with a higher proportion of fine roots in smaller tree sizes, and therefore higher global root turnover rates. RT was determined considering average root turnover rates of 0.915 and 0.019 year−1 for fine and coarse roots for both Eucalyptus species, and 0.786 and 0.049 year−1 for the P. radiata root system. These values were obtained from average values for Eucalyptus and Pinus species, both in a temperate region (Gill and Jackson 2000). A weighted average was used for the turnover rates considering that the ratio of fine to coarse roots is the same as that of leaves plus twigs to the rest of the crown (Mund and Schulze 2006; Scarascia-Mugnozza et al. 2000). As the root biomass equations do not distinguish between stump and the other fractions, the proportion of the stem relative to the crown was considered to be the same as the stump relative to the other root fractions. The weighted average was calculated by assigning a turnover rate of 0 to the stump. RT values were obtained for the same tree dimensional classes as those considered for BT, and the arithmetic average was estimated for all of them. The RT values obtained for each species are shown in Table 3.
Detailed climatic data were compiled for each plot measured and were corrected by considering the elevation of each plot relative to the nearest climate measuring station. Average monthly temperature was corrected by a reduction of 0.5°C and an 8% increase in average monthly precipitation for each 100 m.a.s.l. increment in altitude relative to the climate monitoring station (Aguiló et al. 1995). The July and August precipitation values were not corrected because the precipitation in these months is mainly of convective origin. Climatic data were obtained from the Galician network of climate monitoring stations of the Regional Natural Resources Administration (MeteoGalicia 2011). Average values, representative of each species considered, were estimated for final simulations (Table 1). However, plot-specific values were considered for parameterization validation.
Product and bioenergy module parameterization
For product module parameterization, the average harvested tree size was considered in each logging, and local taper functions (see biomass module parameterization section) were used for product classification for each destination. The threshold limits in the small end for each destination (log wood, pulp wood and slash) are shown in Table 3. Logs and branches with diameter in the big end up to 7 cm, plus foliage, were considered as slash.
Raw material allocation in each production line was carried out according to the real characteristics of the timber market in northern Spain (Toval, per. com.). The raw allocation coefficients considered two alternative silviculture regimes for each species: A, mainly aimed at the chip wood for pulp or board industry, and B, mainly aimed at producing high quality sawn wood, are shown in Table 4. No mill site dump was considered, because all industrial process losses are used for bioenergy, although locally generated biomass combustion ash contains some charcoal (Pérez-Cruzado et al. 2011c; Santalla et al. 2011; Solla-Gullón et al. 2008), the final destination of which may be a mill site dump, or for use as a forest fertilizer or in brick fabrication.
Process loss reallocations to other production lines for all species are shown in Table 4. These were parameterized considering the real intrinsic characteristics of forest product market in northern Spain (Toval, per. com.). Product allocation factors among commodities and their characteristic lifespan and product destination at the end of its useful life are shown in Table 5, and parameters of product destination at the end of life were considered as default for low processing and recycling efficiency (Schelhaas et al. 2004). The lifespan of final products considered was 20 years for long-term products, 10 years for medium-term products, and 1 year for short-term products.
Although product allocation to long-term commodities (Table 5) was higher than considered as default in the low processing and recycling efficiency default parameterization, assumptions are still conservative, since the lifespan was significantly shorter than that considered in other studies (Karjalainen 1996; Karjalainen et al. 1994, 2002; Nabuurs and Sikkema 2001; Row and Phelps 1990). Default bioenergy parameters were considered, except for the slash fuelwood heating value, for which low heating values were local data reported for each species (Pérez et al. 2006, 2008, Table 3).
Model initialization and validation
Since all plots used to parameterize the CO2Fix model were established over former pastureland in which part of the original use is conserved, the average soil organic carbon measured in this part for each species was used to initialize the soil module. Average values of soil organic carbon in the mineral soil up to 30 cm depth for each species studied are shown in Table 2. The biomass module was initialized by considering three different site index values for each species (low, medium, and high) and stand densities according to the silvicultural objectives (see simulated alternatives, below). This enables construction of a specific yield table for each initial condition.
Validation was carried out for the biomass and the soil module using a network of 120 plots located in afforestations on former agricultural land in northwestern Spain, where carbon density (Mg ha−1) has been evaluated in biomass and soil (Pérez-Cruzado et al. 2012). Biomass and soil carbon density were estimated by direct measurements in the field and plotted against values predicted by the CO2Fix model. Since the model was initialized with the specific site index, initial socking, soil carbon content, and specific climatic data for each one of 120 plots, results show the usefulness of the model in the region for predicting changes in C accumulation for the tree species studied for afforestation on former pastureland.
Carbon in above and belowground biomass was estimated directly by establishment of circular plots of radius 10 m, in 40 plots of each species considered, in which diameter at breast height and total height were measured. Biomass was calculated from biomass equations at stand level (see biomass module parameterization section), and values were aggregated at plot level and expressed per hectare. Total carbon in biomass was evaluated from average carbon concentrations observed in each biomass fraction (see biomass module parameterization section).
Soil carbon density (Mg ha−1) was estimated in mineral soil in each plot, to 30 cm depth and in the soil organic layer. For carbon determination in mineral soil, samples were obtained with a soil corer, on 5 occasions in each plot, considering three layers, 0–5, 5–15, and 15–30 cm, to take into account the logarithmic decrease in carbon concentration with soil depth (Jobbágy and Jackson 2000). Bulk density samples (Blake and Hartge 1986) and stoniness were taken into account for soil carbon density estimation with expression (8), where CD is the carbon density in each layer (Mg ha−1), CC is the carbon concentration (as a fraction of unity), Db is the bulk density (g cm−3), T is the thickness (cm), and S is the stoniness (as a fraction of unity).
The litter layer was sampled with a 0.3 × 0.3 m square frame, which was thrown at random on 5 occasions in each plot; all aboveground soil litter within the frame was collected and dried at 40°C until constant weight. The carbon concentration in the organic layer was used to estimate litter carbon density (Pérez-Cruzado et al. 2012). Total soil carbon density was estimated as the sum of carbon density in the organic layer and mineral soil to 30 cm depth. Statistical data on biomass, litter, and soil carbon densities for each species studied are shown in Table 2. To avoid problems related to identifiability of soil compartments in the Yasso model, all were considered jointly for validation and simulation (Palosuo et al. 2006).
Some sensitivity analysis has been carried out for the CO2Fix model (Nabuurs et al. 2008; Palosuo et al. 2008), but little is known about the model sensitivity with three crucial parameters in soil C dynamics, that is, LT, BT, and RT. Since an accurate approach based on local empirical models is described here, the model sensitivity for LT, BT, and RT was determined. Variations of ±10 and ±20% were simulated relative to the estimation of LT, BT, and RT for each species (Table 3). This allowed evaluation of the most sensitive parameters relative to the C accumulation in biomass and soil.
Management alternatives simulated
After model parameterization, two alternative silvicultural alternatives were simulated for each species, with the aim of establishing the baseline carbon sequestration for the species in northern Spain when used in afforestation on former pastureland. The alternatives simulated were as follows: A, aimed at chip wood production for pulp or board industry, and B, aimed at high quality sawn wood production. Details about product parameterization for raw material allocation to production lines for all species and alternatives considered are shown in Table 4. Site indexes considered for each species were as follows: 17, 21, and 25 m at a reference age of 10 years for E. globulus (Fernández López 1982), 10, 14, and 18 at a reference age of 6 years for E. nitens (Pérez-Cruzado 2009), and 13, 18, and 23 m at a reference age of 20 years for P. radiata (Diéguez-Aranda et al. 2005).
The chip wood management alternative (A) for the three species is quite similar in terms of initial stocking and management. This alternative is representative of most Eucalyptus plantations in northern Spain, although silviculture for high quality sawn wood is quite important in P. radiata plantations. Initial stocking for alternative A was 1,400 stems ha−1 for all species, and final cut was simulated at 19, 15, and 12 years for both E. globulus and E. nitens, and 34, 30, and 28 years for P. radiata for each site index, respectively. Neither thinning nor pruning was considered for this management alternative.
The sawn wood management alternative (B) starts at the same initial stocking for the tree species considered (1,400 stem ha−1), but the management applied was quite different. Since this alternative is not appropriate for poor sites, it was only simulated for the two highest site indexes. Management schemes were similar for both eucalypts, with two thinning at ages 4–3 and 8–6 years (for medium and high site index, respectively), with a remaining tree density of 700 and 350 stem ha−1 for each intervention. Three prunings were simulated at ages 2–3, 3–4, and 4–5 years (for medium and high site indexes, respectively), with pruned heights of 2, 4, and 6 m, respectively. Pruning was considered to affect 1,000, 800, and 450 stem ha−1 in each intervention, and pruned branches and leaves were considered to be incorporated into the soil. These silviculture regimes were based on that proposed by Pérez-Cruzado et al. (2011b) for E. nitens. Clearfelling for alternative B was 20 and 16 years for the medium and high site index, respectively, for both E. globulus and E. nitens.
For P. radiata, the sawn wood management alternative (B) is based on that proposed by Rodríguez et al. (2002b). Two thinning were considered at ages 12–10 and 22–20 years (for medium and high site index, respectively), with densities after the operations of 900 and 400 stem ha−1, respectively. Two prunings were considered at ages 8–7 and 15–12 years, with a 1,200 stem ha−1 pruned until 3 m height in the first intervention, and 500 stem ha−1 and affected up to a height of 6 m in the second intervention. Clearfelling was set at 35–30 years for each site index.
Simulations were carried out for the average climate conditions for each species studied (Table 1) and initialized with the average soil organic matter content observed in the pasture for each species (Table 5). Moreover, two options were simulated for the highest site indexes of each species: harvesting of 50% slash for energy production (considered as default in all simulations) or no slash harvesting. The effect on the reductions in emissions derived from soil and bioenergy was assessed for these two options.
Results
Biomass compartment validation
The effect of yield tables selected for P. radiata stands is shown in Fig. 2. It can be seen how both dynamic and static forest-specific models underestimate biomass carbon when high quality afforestation on former agricultural lands is considered. Therefore, a specific model for high quality P. radiata plantations established over former agricultural land was fitted. Results of simultaneous fitting provided good results (Table 6); all parameters were significant (p < 0.005), and the adjusted coefficient of determination was similar to those obtained for the models developed for the other two species (Pérez-Cruzado et al. 2011a). Graphs of observed against predicted biomass C values for E. globulus and E. nitens plantations are shown in Fig. 3. The model prediction works well, because the same plantations were used in developing the models (Pérez-Cruzado et al. 2011a).
Observed against predicted values for aboveground plus belowground biomass carbon in P. radiata plots considering: a the static growth model developed by Castedo-Dorado et al. (2009), b the dynamic growth model developed by Castedo-Dorado et al. (2007), and c a specific model developed for these plots
Observed against predicted values for aboveground plus belowground biomass carbon in a E. globulus and b E. nitens plots, considering the static model developed by Pérez-Cruzado et al. (2011a)
The results of stand biomass models for biomass allocation factors were also satisfactory. The adjusted determination coefficients were higher than 0.93 for all biomass fractions (Table 7), and all parameters were significant (p < 0.05, Table 8). These models were used to determine the biomass fractioning among stem, roots, branches, and leaves at each development stage simulated in the yield tables. Data was referred to stem and set to 1 for implementation in the models.
Soil compartment validation
Soil C density estimations showed a strong bias toward underestimation, results of observed/predicted values for the validation plots are shown in Fig. 4. Estimation for all species studied followed the same pattern, with estimated values similar to observed values for the lower initial carbon contents and much lower than the observed values for the highest carbon contents. The variability in P. radiata was lower than for both Eucalyptus spp., although the same trends were observed for all species in the graphs of observed/predicted values. For a specific estimation of C accumulation in soil, the observed/predicted correction models shown in Fig. 4 can be used.
Sensitivity analysis
The sensitivity analysis for the leaves, branches, and roots turnover is shown in Fig. 5. The Yasso model displayed low sensitivity as regards these parameters, as increments of ±20% in each parameter supposes differences in soil carbon accumulation <0.5% for the 120 plots used for model validation. The model displayed higher sensitivity to root turnover than to branch or leaf turnover.
Model simulation
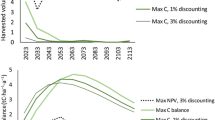
Outputs of the parameterized model are shown in Figs. 6, 7, and 8. These figures show the changes in C stocks over several rotations in the same stand. Assumptions for these outputs imply that yield tables are suitable for all rotations considered, which would be reasonable if no coppice rotations were considered. Another important assumption is that climate will remain unchanged in the study period.
Although there were large oscillations among alternatives, a new equilibrium was reached after afforestation of former agricultural land with the tree species studied for some compartments, namely biomass, products, and soil (Figs. 6, 7, and 8). This implies average C stocks in the stand biomass after land-use change (BS) of 41.1, 52.9, and 66.0 Mg C ha−1 for all alternatives simulated for E. globulus, E. nitens, and P. radiata, respectively (Fig. 6).
Equilibrium C accumulation in products (PS) became an important carbon sink after land-use change. It followed a similar shape as observed for BS and tended to stabilize as time since afforestation increased. The average PS values after land-use change were 91.9, 156.0, and 95.0 Mg C ha−1 for all alternatives simulated for E. globulus, E. nitens, and P. radiata, respectively (Table 9). It must be considered here that no effect of changes in wood products demand nor initial PS was taken into account.
As regards soil, simulations of the alternatives considered are shown in Figs. 6 and 8. The overall change after 100 years for all alternatives simulated was a slight increase in C density in P. radiata stands, whereas in both species of Eucalyptus, the values remained more constant or even decreased for the lowest site index. The C stock equilibrium values in the soil after land-use change (SS) were 80.6, 77.8, and 76.9 Mg C ha−1 for all alternatives simulated for E. globulus, E. nitens, and P. radiata, respectively, considering harvesting of 50% slash for bioenergy. The average value for each compartment considered (BS, PS, and SS) varied depending on the age at which the steady state was considered for each compartment. Thus, the 0 to 200-year period was considered for BS, 125 to 200-year period for PS, and 50 to 200-year period for SS. The C stock values for each species and management alternatives are shown in Table 9.
For all alternatives simulated, the average BS values decreased in the order P. radiata > E. nitens > E. globulus, the average PS values decreased in the order E. nitens > P. radiata > E. globulus, and the SS values decreased in the order E. globulus > E. nitens > P. radiata. Although there were large differences in productivity among the species studied, the simulation results did not differ as regards the order of the three species studied for the initial SOC content in the pasture (Table 2) relative to the SS previously reported.
Because the mitigation effect occurs immediately after bioenergy use, representations in the CO2Fix model are accumulated avoided emissions (Figs. 7 and 8). This makes it difficult to make comparisons with stock changes that occur in other compartments, as previously reported. The avoided C emissions resulting from bioenergy use (BM, Mg C ha−1 year−1) were therefore estimated for each alternative and site quality considering a period of 200 years after land-use change (Table 9). The most effective species for BM when harvesting of 50% slash residues is considered is E. nitens, followed by E. globulus and P. radiata. When harvesting of residues is not considered, both Eucalyptus showed a similar value of BM, double that observed for P. radiata.
Effect of simulated management alternatives
Management alternatives are compared in Figs. 6 and 7, and two biomass extraction methods for bioenergy use are compared in Fig. 8. Results of average C stock in the steady state after land-use change (BS, PS, and SS) and average avoided emissions by energetic use (BM) are summarized for each alternative and species in Table 9.
Management alternative A (chip wood) is more effective, for BS, PS, and BM, relative to alternative B (sawn wood) (Table 9). Site quality played an important role in this aspect, with differences among the same alternative for the C stock in BS as high as ±20, ±19 and ±49% for alternative A, and ±8, ±11 and ±28% for alternative B, for E. globulus, E. nitens, and P. radiata, respectively (Table 9), which shows that the equilibrium C stock in biomass is more sensitive to site index for management alternative A than for alternative B. Management alternatives A and B were therefore compared by considering only the two highest site indexes. On the other hand, alternative A was less effective than alternative B as regards SS for all species considered.
The proportion of harvested slash affects SS, but also BM. The BM increased and SS decreased with increasing proportion of slash harvesting (Figs. 6, 7, and 8; Table 9). Thus, harvesting 50% of slash residues resulted in increases in BM of +9, +28, and +49% for alternative A and of +18, +40, and +28% for alternative B, for E. globulus, E. nitens, and P. radiata, respectively, whereas the predicted decreases in SS were −2, −7, and −4% for alternative A and −4, −8, and −7% for alternative B, for E. globulus, E. nitens, and P. radiata, respectively (Table 9).
Discussion
Dependence on base models and turnover assumptions
The intrinsic stochasticity of yield model parameters implies high variability between forests, and even within a clearly defined forest type because of annual variations in weather conditions, genetic differences and variations in site quality (Nabuurs et al. 2008). Differences in observed/predicted biomass carbon (Figs. 2 and 3) are therefore not due to the CO2Fix model, but to the representativeness of the chosen models. Although the precision of selected forest-specific models for P. radiata have been found to be good enough for forestland (Castedo-Dorado et al. 2007, 2009), the results obtained here demonstrated a slight bias when these models were applied to forest plantations established on former agricultural land. This may be because of the higher average site quality observed in the plots, relative to those used to fit the models. The dynamic model (Castedo-Dorado et al. 2007) worked better than the static model (Castedo-Dorado et al. 2009), but the best estimates were obtained with the afforestation-specific static models (Figs. 2 and 3).
CO2Fix biomass module estimations have also been validated for biomass compartment by other authors (Masera et al. 2003), who reported underestimation of biomass, which they attributed to the fact that the model input data represented managed forest, whereas the published data represented undisturbed forests. Since CO2Fix relies heavily on net annual increment from yield tables (Nabuurs et al. 2008), the user should chose adequate yield tables. This is an important point to be considered when CO2Fix is used for scaling up from stand level to landscape or higher level, where selected sites should represent the average growth conditions of tree species considered and the selected climate zone (Karjalainen et al. 2002). In such cases, this approach may guarantee the representativeness of the yield tables for the scale considered. An average site index weighted by the surface may be appropriate for obtaining the representative yield tables for a given region.
On the other hand, the simulations carried out here considered invariable climatic conditions in the study period for both validation and evaluation alternatives. The main constraint of all empirically based models is that their applicability is restricted to the scope of the original data (Korzukhin et al. 1996), including the climatic conditions.
Results for soil module validation showed that the estimated values were similar to observed values for the lowest carbon densities, whereas the highest carbon densities were greatly underestimated (40–52%) (Fig. 4). Pérez-Cruzado et al. (2012) observed a trend in these same plots with age, where the youngest plots had the lowest carbon densities and the oldest the highest carbon densities. Bias in model outputs were therefore due to overestimation of decomposition rates for the model, which led to greater differences as time since land-use change increased. This effect has also been noted by other authors who parameterized the Yasso model for Eucalyptus spp. (Lemma et al. 2007) and for other species (de Wit et al. 2006; Palosuo et al. 2008). This is attributed to overestimation of decomposition of soil compartments, as well as to the fact that the model parameterization does not consider litter input sources other than trees.
In the CO2Fix model, the effects of climate on decomposition are related to the macroclimate, and some effects of microclimatic conditions on SOC decomposition may not have been taken into account. Lemma et al. (2007) considered that the contribution that different species make to microclimate is small relative to litter input and litter quality, although Pérez-Cruzado et al. (2012) suggested that these differences may be greater. Large differences among species in soil organic carbon evolution after land-use change were also observed in the same plots as those used here for validation, which can be only attributed to species-induced differences in microclimatic conditions (Pérez-Cruzado et al. 2012).
Nabuurs et al. (2008) carried out a sensitivity analysis for the CO2Fix model for temperate and tropical forests and concluded that stem parameters (CAI, density, and carbon content) and initial carbon stock in the most recalcitrant humus (humus type 2, Liski et al. 2005) largely determine the outcome of the model. These authors attributed this to storage of larger amounts of C in stems and humus type 2 than in other fractions (roots, foliage, branches, and other soil compartments) and therefore recommend paying more attention to stem parameter model parameterization. However, the model sensitivity relative to other parameters like LT, BT, and RT is still not clear (de Wit et al. 2006). Moreover, these parameters are not always available, which may lead to too many assumptions and simplifications. A detailed approach is described for BT and RT determination from species-specific allometric relations, whereas LT is estimated from reported values of 3-PG parameters for the species studied.
Turnover parameter estimations (LT, BT, and RT) for the studied species are consistent with those observed for other authors for several species (Schelhaas et al. 2004). With regard to LT, parameter values imply a mean leaf lifespan of 3.1, 3.9, and 2.8 years for E. globulus, E. nitens, and P. radiata, respectively, which are considered reasonable for adult leaves of both Eucalyptus and also for Pinus. The BT values are also in the order of reported by Schelhaas et al. (2004) for several species worldwide. Root turnover is difficult to determine because few studies have been carried out, and the values vary substantially depending on the methodology used. Jourdan et al. (2008) observed differences as large as 0.7–1.8 year−1 depending on methodology used for Eucalyptus plantations in Brazil. The root turnover rate is generally greater than that of leaf turnover (Swift et al. 1979). This parameter takes the same value (0.18 year−1) for the tree species in reported 3-PG parametrizations (Pérez-Cruzado et al. 2011b; Rodríguez et al. 2002a; Sands and Landsberg 2002), but different values are obtained for each species considering the specific sizes distribution and turnover rates in the fine and coarse fraction (Table 3).
Sensitivity analysis for the effects of LT, BT, and RT on soil C estimation showed that the Yasso model is strongly robust with regard to these parameters. All showed deviations <±0.5% with variations of ±20% in the turnover parameter. The robustness of the Yasso model in comparison with alternative soil C models has been studied for other parameters by (Palosuo et al. 2008), who concluded that the Yasso model is more conservative in the estimations of changes in SOC after input of fresh organic matter, because of higher decomposition estimation. Moreover, RT was found to be the most sensitive parameter, probably because root turnover is the most important source of organic matter to mineral soil in temperate forests (Rasse et al. 2001).
Uncertainty in estimates obtained by the CO2Fix model has been found to depend on data availability (Nabuurs et al. 2008). The uncertainty remains very high, even when there is good access to the data, and much higher than can reasonably be achieved in carbon sequestration through changes in forest management. The main sources of uncertainty are that: (i) stem parameters largely determine model outputs, (ii) depending on the initial state of the model, perturbation can lead to multiple equilibria, and (iii) the standard deviation of total carbon stock is twice as high in tropical secondary forest than in temperate forest because of wood density and current annual increment (Nabuurs et al. 2008).
Thus, for the 95% confidence interval, the average values ranged ±24% when data availability was high, and ±86% when data availability was low for the biomass and soil compartments (Nabuurs et al. 2008). A similar degree of uncertainty was observed in CO2Fix (95% confidence levels after 90 years amounted to ±20%) and was considered quite large (Groen et al. 2006). Another national study, in Finland, reported lower levels of uncertainty for the forest and soil (Monni et al. 2007). For direct measurement of the effect for chronosequences and pairwise plots, in the same validation plots in the present study, 95% confidence intervals ranged from ±17 and ±18% only for the soil compartment (Pérez-Cruzado et al. 2012). The bias in the soil estimation is therefore considered a more serious risk than the uncertainty when applying the CO2Fix model.
Nabuurs et al. (2008) observed that the soil made the smallest contribution to the overall uncertainty and attributed this to the small number of parameters and the hidden temperature sensitivity functions in the model, which makes it more robust. The key uncertainty in the soil sink with the Yasso model is the initial value of soil C stock (de Wit et al. 2006), because if soil C stock is not in the steady state relative to decomposition for the climatic conditions simulated, the model may report erroneous trends. One way of correcting this is to run the model until it reaches the steady state. However, this source of uncertainty is reduced in importance when approaching the end of the data series (de Wit et al. 2006).
This was corrected in the present study by considering the average carbon content during the previous land use (pasture) as the average value for the 40 pairwise plots measured for each species considered. Since changes in C in the soil compartment after simulations did not show strong oscillations in the medium term, this approach was considered adequate. As previously reported, other significant sources of uncertainty are the rates of turnover of branches and foliage (de Wit et al. 2006), although in the present study, high data availability enabled accurate estimation.
Mitigation effect of several management alternatives
When evaluating the whole forest system, there are great uncertainties as regards the persistence of the sink and how these temporary sinks should be considered. One attempt to do this is by the advancing mean method described by Nabuurs and Schelhaas (2002). On this paper, the average C stock in the steady stage (BS) was evaluated as the average in the period 0–200 years for the biomass.
Evaluation of the effect of afforestation of former pastureland on C accumulation was applied in the present study, considering the C stock on biomass on pasturelands to be 0. The highest BS was reached in P. radiata stands because of the longer rotation age, which enabled an average C stock of 66.0 Mg C ha−1 to be reached. Management alternative A produced larger C stocks for all species considered than alternative B, because of biomass reduction by thinning (Fig. 6; Table 9). These results are consistent with those of Mund and Schulze (2006), who reported that the total amount of carbon in the system decreased as management intensity increased in Fagus sylvatica stands in Germany. The same effect was reported by Matala et al. (2009) who observed that future evolution of C in the growing stock depends on forest management, as well as on climate-change scenarios. Moreover, BS increased with site quality for all species studied.
Changes in soil C stock were found to depend on the management alternative and site index considered (Figs. 4, 8; Table 9). Initial C losses were observed in all simulations in the first 8 years. This effect was reported by other authors using the same methodology (Nabuurs and Schelhaas 2002) or using empirical data from the same plots (Pérez-Cruzado et al. 2012) and is considered to be a result of ignoring the herbaceous root organic matter input to the soil.
The present results showed that changes in land use have a greater impact on biomass carbon stock than on soil stock, as also reported by other authors (Jandl et al. 2007; de Wit et al. 2006), although soil C is more stable than biomass C. It also takes decades until net gains occur in former pasture soils (Jandl et al. 2007; Pérez-Cruzado et al. 2012). There were slight differences in SS in the simulated period (50–200 year) for the different site indexes and management alternatives considered. The SS increased with site index for all species. Alternative B produced highest C stock in the steady state, because more organic matter was incorporated to the soil in pruning and thinning operations (completely or 50% of residues were left in place). The Yasso model also shows low sensitivity to changes in OM input to the soil than other models (Palosuo et al. 2008), which make the predictions more conservative. It is therefore possible that real differences among alternatives would be greater than predicted here.
The most important factors involving SOC accumulation in afforestation over former agricultural land are changes in: (i) litter production, (ii) litter quality, (iii) the depth to which organic matter is incorporated, (iv) the microclimatic conditions, and (v) the physical and chemical stability of SOM (Lal 2005; Lugo and Brown 1993; Paul et al. 2002; Post and Kwon 2000). Some process-based models are sensitive to these parameters, but the Yasso model is only sensitive to climate conditions, organic matter quality, organic matter input, and initial conditions (Liski et al. 2005), and therefore, only conclusions derived from these effects can be reached. Conditions that are not conducive to soil microbial processes, such as sandy texture, low nutrient availability, and low pH, may lead to the formation of a thick forest floor layer (Jandl et al. 2007). Moreover, microclimatic conditions have been found to affect the changes in SOC in relation to this land-use change (Pérez-Cruzado et al. 2012), although this was not considered in the Yasso model.
Although inclusion of ground vegetation in this type of analysis is not usual, its inclusion may provide more realistic estimation of SOC after land-use change. Because ground vegetation recovers rapidly after thinning and clearcutting, its effect on SOC may result in smoothing of the simulated changes in the soil compartment (Palosuo et al. 2008). Differences among tree species in SS were also observed by using the CO2Fix model to describe the same land-use change as studied here (Lemma et al. 2007).
As it is not yet clear how carbon in wood products will be credited, it is important to compare the total outcome of the scenarios with and without products (de Jong et al. 2007). If products are not considered, all C in products is taken into account as net emission at harvest. If products are considered, the balance between new products being produced and old products being decomposed may also provide a net sink in products-in-use (Nabuurs and Schelhaas 2002). Thus, a new pool appears with forest product use, with a double mitigating effect: by carbon sequestering in its own matter, and by substituting alternative products for which fossil C releases are needed. For this hypothesis to hold true, it must be proved that the C balance in wood product use is more favorable than natural mortality processes. Profft et al. (2009) reported that the mean residence time is higher in wood products than in dead wood for the conditions in central Germany, which implies that use of wood products results in a carbon sink that otherwise would not exist.
Carbon in forest products was considered as an additional pool in the present study, and average C stock in the steady state (PS) was calculated for the period 125–200 years after land-use change. Under the assumptions of product lifespan considered (Table 5), the total C stock in forest products is greater than those in biomass (Table 9). However, estimating PS exclusively from products production and lifespan supposes that wood products demands do not play any role, whereas in a scenario of decreasing wood products demand, C in product stock in use can also act as a C source. It must also be considered that C stock in products was not initialized, since actual PS is unknown, and decreases respect to actual PS level would be possible. Site index had an important effect on product stock, with PS increasing with site index. In comparison with other studies, De Jong et al. (2007) observed similar C stocks in the product pool (40–65 Mg C ha−1) in the oak forest of Central Highlands of Michoacán (Mexico).
Although some authors have observed that low forest utilization yielded more forest products than the high utilization system (Harmon and Marks 2002), the results of the present study demonstrate that alternative A generates more C stock in the products than alternative B. This may be due to the difference in the assumptions regarding lifespan, since a larger proportion of long-term products are generated in management alternative B than in alternative A. Other authors considered lifespan periods for the different product groups of 50, 16, 4, and 1 year for long, medium-long, medium-short, and short life span products, respectively (Karjalainen 1996; Karjalainen et al. 1994, 2002; Nabuurs and Sikkema 2001; Row and Phelps 1990). The assumptions used here as regards the product lifespan can be considered as conservative, and PS may actually be larger. Silviculture also affects the lifespan of harvested products; for instance, thinning from above leads to a mean residence time of 23 year and thinning from below to a residence time of 18 year (Profft et al. 2009). The latter author reported an average residence time in wood products of 20 year, which was the longest life span considered in the study.
On the other hand, not all this PS can be considered directly as avoided emissions, since there are additional releases from fossil fuel sources in the delivery chain and industrial processes. A complete study considering life cycle assessment and forest carbon analysis may report different results than obtained in the present study (e.g., McKechnie et al. 2011). In a recent study on fuel consumption in road transport of round wood in Austria (Holzleitner et al. 2010), the emission per cubic meter of roundwood due exclusively to transport was 2.23 kg C m−3, considering an average lorry load of 25 m3 and an average distance (forest industry) of 51 km. This emission must be discounted from the C gain derived from use of wood products.
Other forest products must be considered as flux rather than stock, that is, bioenergy production. The mitigating effect of bioenergy production (BM) is the only strictly long-term mitigating potential of forest systems (Lindner and Karjalainen 2007), as the other pools considered reach equilibrium after land-use change, and the accumulation effect becomes limited. BM was higher in alternative A than in alternative B. This follows the same trend as PS, because some of the energy use occurs with the log wood and pulp wood waste and recycling processes, and the other part occurs with the slash. Values of BM obtained in this study are higher than those reported by de Jong et al. (2007) for the bioenergy scenario, which resulted in continuous stream of about 1.36 Mg C ha−1 year−1, even in the case of no slash harvesting. The effect of site index was the same as observed for the other compartments, that is, the higher the site index the greater mitigation rate through bioenergy use.
The avoided emissions through bioenergy substitution depend on the biomass transformation procedure, the technology transformation efficiency, and the substituted energy source. Although the main procedure is combustion to produce thermal energy, where the substituted product is fuel, conversion to electricity also occurs to some extent. In this case, the avoided emissions depend on the specific contribution of each energy supply, and its characteristic C balance.
The effects of the intensity of slash harvesting on BM are shown in Table 9, with increments of between 18 and 40% for harvesting 50% of slash relative to no slash harvesting. On the other hand, harvesting 50% of slash results in decreases of between 4 and 8% of soil C equilibrium stock. This effect has also been observed by other authors (Johnson and Curtis 2001). Some studies have shown that the gain in SOC obtained by leaving harvesting residues in the field is stronger in coniferous than in broadleaved species (Hendrickson et al. 1989; Johnson and Todd 1998; Knoepp and Swank 1997; Mattson and Swank 1989), although some studies in coniferous forests and in mixed forests have also shown little or no effect of residues on soil C or N (Olsson et al. 1996; Johnson et al. 2002). The greatest effects on both SS decreases and in BM increases were in E. nitens, probably because of its high yield and crown biomass (Pérez-Cruzado et al. 2011a). Logging residues left in place have been found to be greatly influenced by the top diameter threshold considered (Räisänen and Nurmi 2011), and slash production was almost doubled, with increments of 2 cm in the top diameter threshold, which adds uncertainty to the absolute slash residues estimation.
Studies of the global carbon cycle in relation to bioenergy systems conclude that although there may be some decrease in soil carbon associated with biomass production, this is negligible in comparison with the contribution of bioenergy systems toward greenhouse mitigation by avoiding fossil fuel emissions (Cowie et al. 2006). Moreover, the effect of harvesting residues on SOC is time limited, because C and N increase temporally because of residues becoming incorporated into the soil (Black and Harden 1995, Knoepp and Swank 1997, Smethurst and Nambiar 1990), and the increase in soil C and N is short-lived [less than 4 years, according Smethurst and Nambiar (1990)]. Nevertheless, some authors have reported that intensified biomass extraction slightly decreased forest growth and thus the biomass carbon stock and litter input to the soil (Helmisaari et al. 2011; Palosuo et al. 2008).
According to the results obtained in the present study, a combination of bioenergy and carbon sequestration will be the best option for mitigating CO2 emissions in the long term, as already reported for plantation management in other countries (de Jong et al. 2007; Kaul et al. 2010). Nevertheless, potential negative impacts on forest C mitigation effect may occur by bioenergetic use, relative to indirect emissions by reducing slash C stock because of the delay in slash residues decomposition (Repo et al. 2011), or when approaches other than stock change are considered, that is, life cycle assessment (McKechnie et al. 2011).
Conclusions
The CO2Fix model was parameterized for fast growing tree plantations with E. globulus, E. nitens, and P. radiata established over former pastureland. Specific models for these afforestation were required to obtain reliable results of biomass accumulation and the model provided underestimations of soil carbon. The equilibrium C stock in the products after simulation of management alternatives through infinite rotations was greater than those in living biomass. Differences were found among species in their ability to store carbon in the long term in form of biomass, products, and in the soil, but Pinus radiata was the only species able to provide increases in soil carbon related to the former pasture use. A 50% reduction in slash harvesting resulted in a 18–40% increases in the bioenergy mitigating effect, whereas soil equilibrium C stock decreased by only 4–8% relative to no slash harvesting. The silvicultural alternative aimed at chip wood production was the most effective in storing carbon in biomass, products, and bioenergy, whereas the sawn wood production regime was more effective for storing carbon in the soil because of the more frequent slash input derived from pruning and thinning.
References
Aguiló M, Aramburu MP, Blanco A, Calatayud T, Carrasco RM, Castilla G, Castillo V, Ceñal MA, Cifuentes P, Díaz M, Díaz A, Escribano R, Escribano MM, Frutos M, Galiana F, García A, Glaria G, González S, González C, Iglesias E, Martín A, Martínez E, Milara R, Monzón A, Ortega C, Otero I, Pedraza J, Pinedo A, Puig J, Ramos A, Rodríguez I, Sanz MA, Tevar G, Torrecilla I, Yoldi I, Rhea SA (1995) Guía para la elaboración de estudios del medio físico: contenido y metodología. Ministerio de Medio Ambiente, Secretaría General del Medio Ambiente, Madrid
Alvarez E, Fernández Marcos ML, Torrado V, Fernández Sanjurjo MJ (2008) Dynamics of macronutrients during the first stages of litter decomposition from forest species in a temperate area (Galicia, NW Spain). Nutr Cycl Agroecosyst 80:243–256. doi:10.1007/s10705-007-9140-4
Balboa-Murias MA, Rodríguez-Soalleiro R, Merino A, Álvarez-González JG (2006) Temporal variations and distribution of carbon stocks in aboveground biomass of radiata pine and maritime pine pure stands under different silvicultural alternatives. For Ecol Manage 237:29–38. doi:10.1016/j.foreco.2006.09.024
Black TA, Harden JW (1995) Effect of timber harvest on soil carbon storage at Blodgett Experimental Forest, California. Can J For Res 25:1385–1396. doi:10.1139/x95-151
Blake GR, Hartge KH (1986) Bulk density. In: Klute A (ed) Methods of soil analysis, 2nd edn. ASA and SSAA, Madison, pp 363–375
Böttcher H, Lindner M (2010) Managing forest plantations for carbon sequestration today and in the future. In: Bauhus J, van der Meer P, Kanninen M (eds) Ecosystem goods and services from plantation forests. Earthscan Ltd., London, pp 43–76
Brañas J, González-Río F, Rodríguez Soalleiro R, Merino A (2000) Biomasa maderable y no maderable en plantaciones de eucalipto. Cuantificación y estimación. CIS-Madera 4:72–75
Castedo-Dorado F, Diéguez-Aranda U, Álvarez-González JG (2007) A growth model for Pinus radiata D. Don stands in north-western Spain. Ann For Sci 64:453–465. doi:10.1051/forest:2007023
Castedo-Dorado F, Crecente-Campo F, Álvarez-Álvarez P, Barrio-Anta M (2009) Development of a stand density management diagram for radiate pine stands including assessment and stability. Forestry 82:1–15. doi:10.1093/forestry/cpm032
Cowie AL, Smith P, Johnson D (2006) Does soil carbon loss in biomass production systems negate the greenhouse benefits of bioenergy? Mitig Adapt Strat Global Change 11:979–1002. doi:10.1007/s11027-006-9030-0
Crecente-Campo F (2008) Modelo de crecimiento de árbol individual para Pinus radiata D. Don en Galicia. Dissertation or Thesis, University of Santiago de Comostela
de Jong BH, Masera O, Olguin M, Martinez R (2007) Greenhouse gas mitigation potential of combining forest management and bioenergy substitution: a case study from Central Highlands of Michoacán, Mexico. For Ecol Manage 242:398–411. doi:10.1016/j.foreco.2007.01.057
de Wit HA, Palosuo T, Hylen G, Liski J (2006) A carbon budget of forest biomass and soils in southeast Norway calculated using a widely applicable method. For Ecol Manage 225:15–26. doi:10.1016/j.foreco.2005.12.023
Diéguez-Aranda U, Burkhart HE, Rodríguez-Soalleiro R (2005) Modeling dominant height growth of radiata pine (Pinus radiata D. Don) plantations in north-western Spain. For Ecol Manage 215:271–284. doi:10.1016/j.foreco.2005.05.015
EU (1992) Council regulation (EEC) No 2080/92 of 30 June 1992 Instituting a Community aid Scheme for Forestry Measures in Agriculture
Fernández López AB (1982) Evaluación de la producción y productividad del monte bajo de Eucalyptus globulus. Consellería de Agricultura, Gandería e Montes. Centro de Investigaciones Forestales de Lourizán, Pontevedra, p 69
Gill RA, Jackson RB (2000) Global patterns of root turnover for terrestrial ecosystems. New Phytol 147:13–31. doi:10.1046/j.1469-8137.2000.00681.x
Groen T, Nabuurs G, Schelhaas M (2006) Carbon accounting and cost estimation in forestry projects using CO2Fix V. 3. Climatic Change 1:269–288. doi:10.1007/s10584-006-1827-z
Harmon ME, Marks B (2002) Effects of silvicultural practices on carbon stores in Douglas-fir–western hemlock forests in the Pacific Northwest, USA: results from a simulation model. Can J For Res 32:863–877. doi:10.1139/X01-216
Helmisaari HS, Hanssen KH, Jacobson S, Kukkola M, Luiro J, Saarsalmi A, Tamminen P, Tveite B (2011) Logging residue removal after thinning in Nordic boreal forests: long-term impact on tree growth. For Ecol Manage 11:1919–1927. doi:10.1016/j.foreco.2011.02.015
Hendrickson OQ, Chatarpaul L, Burgess D (1989) Nutrient cycling following whole-tree and conventional harvest in northern mixed forest. Can J For Res 19:725–735. doi:10.1139/x89-112
Holzleitner F, Kanzian C, Stampfer K (2010) Analyzing time and fuel consumption in road transport of round wood with an onboard fleet manager. Eur J Forest Res 130:1–9. doi:10.1007/s10342-010-0431-y
IUSS Working Group WRB (2006) World reference base for soil resources 2006. World soil resources reports no. 103. FAO, Rome
Jandl R, Lindner M, Vesterdal L, Bauwens B, Baritz R, Hagedorn F, Johnson DW, Minkkinen K, Byne KA (2007) How strongly can forest management influence soil carbon sequestration? Geoderma 137:253–268. doi:10.1016/j.geoderma.2006.09.003
Jobbágy EG, Jackson RB (2000) The vertical distribution of soil organic carbon and its relation to climate and vegetation. Ecol Appl 10:423–436. doi:10.1890/1051-0761(2000)010[0423:TVDOSO]2.0.CO%3B2
Johnson DW, Curtis PS (2001) Effects of forest management on soil C and N storage: meta analysis. For Ecol Manage 140:227–238. doi:10.1016/S0378-1127(00)00282-6
Johnson DW, Todd DEJ (1998) Harvesting effects on long-term changes in nutrient pools of mixed oak forest. Soil Sci Soc Am J 62:1725–1735. doi:10.2136/sssaj1998.03615995006200060034x
Johnson DW, Knoepp JD, Swank WT, Shan J, Morris LA, Van Lear DH, Kapeluck PR (2002) Effects of forest management on soil carbon: results of some long-term resampling studies. Environ Pollut 116:201–208
Jourdan C, Silva EV, Gonçalves JLM, Ranger J, Moreira RM, Laclau JP (2008) Fine root production and turnover in Brazilian Eucalyptus plantations under contrasting nitrogen fertilization regimes. For Ecol Manage 256:396–404. doi:10.1016/j.foreco.2008.04.034
Karjalainen T (1996) Dynamics and potentials of carbon sequestration in managed stands and wood products in Finland under changing climatic conditions. For Ecol Manage 80:113–132. doi:10.1016/0378-1127(95)03634-2
Karjalainen T, Kellomäki S, Pussinen A (1994) Role of wood-based products in absorbing atmospheric carbon. Silva Fenn 28:67–80
Karjalainen T, Pussinen A, Liski J, Nabuurs GJ, Erhard M, Eggers T, Sonntag M, Mohren GMJ (2002) An approach towards an estimate of the impact of forest management and climate change on the European forest sector carbon budget: Germany as a case study. For Ecol Manage 162:87–103. doi:10.1016/S0378-1127(02)00052-X
Kaul M, Mohren GMJ, Dadhwal VK (2010) Carbon storage and sequestration potential of selected tree species in India. Mitig Adapt Strat Global Change 15:489–510. doi:10.1007/s11027-010-9230-5
Kauppi PE, Sedjo RJ, Apps MJ, Cerri CC, Fujimori T, Janzen H, Krankina O, Makundi W, Marland G, Masera O, Nabuurs GJ, Razali W, Ravindranath NH (2001) Technical and economic potential of options to enhance, maintain and manage biological carbon reservoirs and geo-engineering. In: Metz et al. (ed) Mitigation, IPPC Third assessment report. Cambridge University Press, Cambridge, UK, pp 302–343
Knoepp JD, Swank WT (1997) Forest management effects on surface soil carbon and nitrogen. Soil Sci Soc Am J 61:928–935. doi:10.2136/sssaj1997.03615995006100030031x
Korzukhin MD, Ter-Mikaelian MT, Wagner RG (1996) Process versus empirical models: which approach for forest ecosystem management? Can J For Res 26:879–887. doi:10.1139/x26-096
Lal R (1999) Soil management and restoration for C sequestration to mitigate the accelerated greenhouse effect. Prog Environ Sci 1:307–326
Lal R (2005) Forest soils and carbon sequestration. For Ecol Manage 220:242–258. doi:10.1016/j.foreco.2005.08.015
Landsberg JJ, Waring RH (1997) A generalised model of forest productivity using simplified concepts of radiation-use efficiency, carbon balance and partitioning. For Ecol Manage 95:209–228. doi:10.1016/S0378-1127(97)00026-1
Lemma B, Kleja DB, Olsson M, Nilsson I (2007) Factors controlling soil organic carbon sequestration under exotic tree plantations: a case study using the CO2Fix model in southwestern Ethiopia. For Ecol Manage 252:124–131. doi:10.1016/j.foreco.2007.06.029
Lindner M, Karjalainen T (2007) Carbon inventory methods and carbon mitigation potentials of forests in Europe: a short review of recent progress. Eur J Forest Res 126:149–156. doi:10.1007/s10342-006-0161-3
Liski J, Palosuo T, Peltoniemi M, Sievänen R (2005) Carbon and decomposition model Yasso for forest soils. Ecol Modell 189:168–182. doi:10.1016/j.ecolmodel.2005.03.005
Lugo AE, Brown S (1993) Management of tropical soils as sinks or sources of atmospheric carbon. Plant Soil 149:27–41. doi:10.1007/BF00010760
Masera OR, Garza-Caligaris JF, Kanninen M, Karjalainen T, Liski J, Nabuurs GJ, Pussinen A, De Jong BHJ, Mohren GMJ (2003) Modeling carbon sequestration in afforestation, agroforestry and forest management projects: the CO2FIX V. 2 approach. Ecol Model 164:177–199. doi:10.1016/S0304-3800(02)00419-2
Matala J, Kärkkäinen L, Härkönen K, Kellomäki S, Nuutinen T (2009) Carbon sequestration in the growing stock of trees in Finland under different cutting and climate scenarios. Eur J Forest Res 128:493–504. doi:10.1007/s10342-009-0299-x
Mattson KG, Swank WT (1989) Soil and detrital carbon dynamics following forest cutting in the southern Appalachians. Biol Fertility Soils 7:247–253. doi:10.1007/BF00709656
McKechnie J, Colombo S, Chen J, Mabee W, MacLean HL (2011) Forest bioenergy or forest carbon? Assessing trade-offs in greenhouse gas mitigation with wood-based fuels. Environ Sci Tech 45:789–795. doi:10.1021/es1024004
Merino A, Balboa MA, Rodríguez-Soalleiro R, González JG (2005) Nutrient exports under different harvesting regimes in fast-growing forest plantations in southern Europe. For Ecol Manage 207:325–339. doi:10.1016/j.foreco.2004.10.074
MeteoGalicia (2011) Servicio Meteorolóxico de Galicia. In: MeteoGalicia. Consellería de Medio Ambiente, Territorio e Infraestructuras. Available via Rede de estacions climáticas da Xunta de Galicia. http://www2.meteogalicia.es/galego/observacion/estacions/listaEstacions.asp. Accessed 15 June 2009
Mohren GMJ, Goldewijk K (1990) CO2FIX: a dynamic model of the CO2-fixation in forest stands. De Dorschkamp, Research Institute for forestry and urban Ecology, Wageningen
Mohren GMJ, Caligaris JFG, Masera O, Kanninen M, Karjalainen T, Nabuurs GJ (1999) CO2FIX for Windows: a dynamic model of the CO2 fixation in forest stands. Institute for Forestry and Nature Research, Instituto de Ecologia, UNAM, Centro Agronomico Tropical de Investigacion y Ensenanza (CATIE), European Forest Institute.Wageningen The Netherlands, Morelia Mexico, Turrialba Costa Rica, Joensuu Finland, p 27
Monni S, Peltoniemi M, Palosuo T, Lehtonen A, Mäkipää R, Savolainen I (2007) Uncertainty of forest carbon stock changes–implications to the total uncertainty of GHG inventory of Finland. Clim Change 81:391–413. doi:10.1007/s10584-006-9140-4
Mund M, Schulze ED (2006) Impacts of forest management on the carbon budget of European beech (Fagus sylvatica) forests. Allg Forst Jagdztg 177:47–63
Nabuurs GJ, Schelhaas MJ (2002) Carbon profiles of typical forest types across Europe assessed with CO2FIX. Ecol Ind 1:213–223. doi:10.1016/S1470-160X(02)00007-9
Nabuurs GJ, Sikkema R (2001) International trade in wood products: its role in the land use change and forestry carbon cycle. Clim Change 49:377–395. doi:10.1023/A:1010732726540
Nabuurs GJ, Garza-Caligaris JF, Kanninen M, Karjalainen T, Lapvetelainen T, Liski J, Masera O, Mohren GMJ, Olgin M, Pussinen A, Schelhaas M (2002) CO2FIX V2.0. Manual of a model for quantifying carbon sequestration in forest ecosystems and wood products. Alterra, Wageningen, The Netherlands
Nabuurs GJ, van Putten B, Knippers TS, Mohren GMJ (2008) Comparison of uncertainties in carbon sequestration estimates for a tropical and a temperate forest. For Ecol Manage 256:237–245. doi:10.1016/j.foreco.2008.04.010
Nutto L, Touza Vázquez MC (2004) Producción de Madera de Sierra de alta Calidad con Eucalyptus globulus. CIS-Madera 12:6–18
O’Grady AP, Worledge B, Battaglia M (2005) Temporal and spatial changes in fine root distributions in a young Eucalyptus globulus stand in southern Tasmania. For Ecol Manag 214:373–383. doi:10.1016/j.foreco.2005.04.021
Olsson BA, Staaf H, Lundkvist H, Bengtsson J, Kaj R (1996) Carbon and nitrogen in coniferous forest soils after clear-felling and harvests of different intensity. For Ecol Manage 82:19–32. doi:10.1016/0378-1127(95)03697-0
Palosuo T, Pia S, Sievänen R, Liski J (2006) Global identifiability as a prerequisite for model parameterisation–the case of soil carbon model yasso. In: Commault C, Marchand N (eds) Lecture notes in control and information sciences. 341. Positive systems. Springer, Heidelberg, pp 129–136
Palosuo T, Peltoniemi M, Mikhailov A, Komarov A, Faubert P, Thürig E, Lindner M (2008) Projecting effects of intensified biomass extraction with alternative modelling approaches. For Ecol Manage 255:1423–1433. doi:10.1016/j.foreco.2007.10.057
Parresol BR (2001) Additivity of nonlinear biomass equations. Can J For Res 31:865–878. doi:10.1139/x00-202
Paul KI, Polglase PJ, Nyakuengama JG, Khanna PK (2002) Change in soil carbon following afforestation. For Ecol Manage 168:241–257. doi:10.1016/S0378-1127(01)00740-X
Pérez S, Renedo CJ, Ortiz A, Mañana M, Silió D (2006) Energy evaluation of the Eucalyptus globulus and the Eucalyptus nitens in the north of Spain (Cantabria). Thermochim Acta 451:57–64. doi:10.1016/j.tca.2006.08.009
Pérez S, Renedo CJ, Ortiz A, Manana M (2008) Energy potential of waste from 10 forest species in the North of Spain (Cantabria). Bioresour Technol 99:6339–6345. doi:1016/j.biortech.2007.12.014
Pérez-Cruzado C (2009) Herramientas de gestión para plantaciones de Eucalyptus nitens (Deane & Maiden) Maiden con el objetivo de fijación de carbono 77 (in Spanish)
Pérez-Cruzado C, Rodríguez Soalleiro R (2011) Improvement in accuracy of aboveground biomass estimation in Eucalyptus nitens plantations: effect of bole sampling intensity and explanatory variables. For Ecol Manage 261:2016–2028. doi:10.1016/j.foreco.2011.02.028
Pérez-Cruzado C, Merino A, Rodríguez-Soalleiro R (2011a) A management tool for estimating bioenergy production and carbon sequestration in Eucalyptus globulus and Eucalyptus nitens grown as short rotation woody crops in north-west Spain. Biomass Bioenerg 35:2839–2851. doi:10.1016/j.biombioe.2011.03.020
Pérez-Cruzado C, Muñoz-Sáez F, Basurco F, Riesco G, Rodríguez-Soalleiro R (2011b) Combining empirical models and the process-based model 3-PG to predict Eucalyptus nitens plantations growth in Spain. For Ecol Manage 262:1067–1077. doi:10.1016/j.foreco.2011.05.045
Pérez-Cruzado C, Solla-Gullón F, Merino A, Rodríguez-Soalleiro R (2011c) Analysis of growth and nutrition of a young Castanea × coudercii plantation after application of wood-bark ash. Eur J Forest Res 130:209–217. doi:10.1007/s10342-010-0422-z
Pérez-Cruzado C, Mansilla-Salinero PN, Merino A, Rodríguez-Soalleiro R (2012) Influence of tree species on carbon sequestration in afforested pastures in a humid temperate region. Plant Soil (in press). doi:10.1007/s11104-011-1035-0
Post WM, Kwon KC (2000) Soil carbon sequestration and land-use change: processes and potential. Global Change Biol 6:317–327. doi:10.1046/j.1365-2486.2000.00308.x
Profft I, Mund M, Weber GE, Weller E, Schulze ED (2009) Forest management and carbon sequestration in wood products. Eur J Forest Res 128:399–413. doi:10.1007/s10342-009-0283-5
Räisänen T, Nurmi J (2011) Impacts of changing the minimum diameter of roundwood on the accumulation of logging residue in first thinnings of Scots pine and Norway spruce. Biomass Bioenergy 35:2674–2682. doi:10.1016/j.biombioe.2011.03.002
Rasse DP, Longdoz B, Ceulemans R (2001) TRAP: a modelling approach to below-ground carbon allocation in temperate forests. Plant Soil 229:281–293. doi:10.1023/A:1004832119820
Repo A, Tuomi M, Liski J (2011) Indirect carbon dioxide emissions from producing bioenergy from forest harvest residues. GCB Bioenergy 3:107–115. doi:10.1111/j.1757-1707.2010.01065.x
Resh SC, Battaglia M, Worledge D, Ladiges S (2003) Coarse root biomass for eucalypt plantations in Tasmania, Australia: sources of variation and methods for assessment. Trees 17:389–399. doi:10.1007/s00468-003-0250-6
Rodríguez R, Espinosa M, Real P, Inzunza J (2002a) Analysis of productivity of radiata pine plantations under different silvicultural regimes using the 3-PG process-based model. Aust For 65:165–172
Rodríguez R, Sánchez F, Gorgoso J, Castedo F, López C, Gadow K (2002b) Evaluating standard treatment options for Pinus radiata plantations in Galicia (north-western Spain). Forestry 75:273–284. doi:10.1093/forestry/75.3.273
Row C, Phelps RB (1990) Tracing the flow of carbon through the US forest products sector. In: Proceedings of the presentation at the 19th world congress IUFRO, p 13
Sánchez F, Ucha P, Rojo A (2004) Stem taper functions and volume equations with product classification for Eucalyptus globulus Labill. in Galicia (NW Spain)
Sands PJ, Landsberg JJ (2002) Parameterisation of 3-PG for plantation grown Eucalyptus globulus. For Ecol Manage 163:273–292. doi:10.1016/S0378-1127(01)00586-2
Santalla M, Omil B, Rodríguez-Soalleiro R, Merino A (2011) Effectiveness of wood ash containing charcoal as a fertilizer for a forest plantation in a temperate region. Plant Soil 1–16, (in press). doi:10.1007/s11104-011-0794-y
SAS Institute Inc (2004) SAS/STAT 9.1 User’s guide. Cary, NC
Scarascia-Mugnozza G, Bauer GA, Persson H, Matteucci G, Masci A (2000) Tree biomass, growth and nutrient pools. In: Schulze ED (ed) Carbon and nitrogen cycling in European forest ecosystems. Springer Verlag, Heidelberg, pp 49–62
Schelhaas MJ, van Esch PW, Groen TA, de Jong BHJ, Kanninen M, Liski J, Masera O, Mohren GMJ, Nabuurs GJ, Palosuo T, Pedroni L, Vallejo A, Vilén T (2004) CO2FIX V 3.1 A modelling framework for quantifying carbon sequestration in forest ecosystems. Alterra, Wageningen
Smethurst PJ, Nambiar EKS (1990) Distribution of carbon and nutrients and fluxes of mineral nitrogen after clear-felling a Pinus radiata plantation. Can J For Res 20:1490–1497. doi:10.1139/x90-197
Solla-Gullón F, Santalla M, Perez-Cruzado C, Merino A, Rodriguez-Soalleiro R (2008) Response of Pinus radiata seedlings to application of mixed wood-bark ash at planting in a temperate region: nutrition and growth. For Ecol Manage 255:3873–3884. doi:10.1016/j.foreco.2008.03.035
Swift MJ, Heal OW, Anderson JM (1979) Decomposition in terrestrial ecosystems. Blackwell, Oxford
Tolosana E (2009) Manual técnico para el aprovechamiento y elaboración de biomasa forestal. 348 (in Spanish)
UNFCCC (1997) The Kioto Protocol. United Nations framework convention on climate change. United Nations Office, Geneva
UNFCCC (2001) Review of the implementation of commitments and of other provisions of the convention, preparations for the first session of the conference of the parties serving as the meeting of the parties to the Kyioto Protocol (Decision 8/CP.4), Decision %/CP.6, Implementation of the Buenos Aires plan of action. United Nations Framework Convention on Climate Change, United Nations Office, Geneva
Acknowledgments
The authors thank Luis Manuel Rodriguez DaCosta for assisting with fieldwork. The study was funded by the Spanish Ministry of Education and Science (AGL2009-13400-C05-04, AGL2010-22308-CO2-01/FOR) and a FPU-MEC (AP2007-04367) Spanish Fellowship awarded to CP-C.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by C. Ammer.
This article originates from the international symposium “Managed Forests in Future Landscapes. Implications for Water and Carbon Cycles (COST action FP 0601 FORMAN).”
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Pérez-Cruzado, C., Mohren, G.M.J., Merino, A. et al. Carbon balance for different management practices for fast growing tree species planted on former pastureland in southern Europe: a case study using the CO2Fix model. Eur J Forest Res 131, 1695–1716 (2012). https://doi.org/10.1007/s10342-012-0609-6
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10342-012-0609-6