Abstract
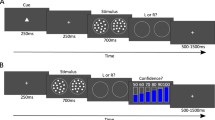
Putative metacognition data in animals may be explained by non-metacognition models (e.g., stimulus generalization). The primary objective of the present study was to develop a new method for testing metacognition in animals that may yield data that can be explained by metacognition but not by non-metacognition models. Next, we used the new method with rats. Rats were first presented with a brief noise duration which they would subsequently classify as short or long. Rats were sometimes forced to take an immediate duration test, forced to repeat the same duration, or had the choice to take the test or repeat the duration. Metacognition, but not an alternative non-metacognition model, predicts that accuracy on difficult durations is higher when subjects are forced to repeat the stimulus compared to trials in which the subject chose to repeat the stimulus, a pattern observed in our data. Simulation of a non-metacognition model suggests that this part of the data from rats is consistent with metacognition, but other aspects of the data are not consistent with metacognition. The current results call into question previous findings suggesting that rats have metacognitive abilities. Although a mixed pattern of data does not support metacognition in rats, we believe the introduction of the method may be valuable for testing with other species to help evaluate the comparative case for metacognition.




Similar content being viewed by others
Notes
An animal could maximize the number of pellets obtained by choosing to repeat the stimulus in every trial (thereby obtaining a pellet for selecting the repeat response followed by pellets for a correct duration-classification response). However, this outcome is unlikely to occur because delay discounting (i.e., the observation that reward value declines as a function of delay to reward) in rats (Cardinal et al. 2001; Mazur 1988, 2007; Richards et al. 1997) argues against the choice of a small, immediate reward followed by a large, delayed reward when a large, immediate reward is currently available.
Although we assume that two exposures of the same duration may allow the animal to integrate information from both stimulus presentations and thereby reduce its perceptual error about the stimulus, other possibilities exist. For example, an animal might limit the impact of a second presentation to cases in which it requested a repeat of the stimulus. In our simulations of a response-strength model, we parametrically explore how much weight the animal assigns to first and second stimulus presentations. We consider the full range from all weight assigned to the first stimulus to all weight assigned to the second stimulus and several intermediate weightings between these two extremes. See “Simulation” section.
References
Basile BM, Hampton RR, Suomi SJ, Murray EA (2009) An assessment of memory awareness in tufted capuchin monkeys (Cebus apella). Anim Cogn 12:1169–1180
Beran MJ, Smith JD, Coutinho MVC, Couchman JJ, Boomer J (2009) The psychological organization of “uncertainty” responses and “middle” responses: a dissociation in capuchin monkeys (Cebus apella). J Exp Psychol Anim Behav Proc 35:371–381
Budson AE, Dodson CS, Daffner KR, Schacter DL (2005) Metacognition and false recognition in Alzheimer’s disease: further exploration of the distinctiveness heuristic. Neuropsychology 19:253–258
Call J (2010) Do apes know that they could be wrong? Anim Cogn 13:689–700
Call J, Carpenter M (2001) Do apes and children know what they have seen? Anim Cogn 4:207–220
Cardinal RN, Pennicott DR, Sugathapala CL, Robbins TW, Everitt BJ (2001) Impulsive choice induced in rats by lesions of the nucleus accumbens core. Science 292:2499–2501
Church RM, Deluty MZ (1977) Bisection of temporal intervals. J Exp Psychol Anim Behav Proc 3:216–228
Crystal JD, Foote AL (2009) Metacognition in animals. Comp Cogn Behav Rev 4:1–16
Emery NJ, Clayton NS (2001) Effects of experience and social context on prospective caching strategies by scrub jays. Nature 414:443–446
Foote AL, Crystal JD (2007) Metacognition in the rat. Curr Biol 17:551–555
Gibbon J (1981) On the form and location of the psychometric bisection function for time. J Math Psychol 24:58–87
Hampton RR (2001) Rhesus monkeys know when they remember. Proc Natl Acad Sci USA 98:5359–5362
Hampton RR (2009) Multiple demonstrations of metacognition in nonhumans: converging evidence or multiple mechanisms? Comp Cogn Behav Rev 4:17–28
Hampton RR, Zivin A, Murray EA (2004) Rhesus monkeys (Macaca mulatta) discriminate between knowing and not knowing and collect information as needed before acting. Anim Cogn 7:239–246
Inman A, Shettleworth SJ (1999) Detecting metamemory in nonverbal subjects: a test with pigeons. J Exp Psychol Anim Behav Proc 25:389–395
Jozefowiez J, Cerutti DT, Staddon JER (2009a) The behavioral economics of choice and interval timing. Psychol Rev 116:519–539
Jozefowiez J, Staddon JER, Cerutti DT. (2009b) Metacognition in animals: how do we know that they know? Comp Cogn Behav Rev 4:29–39
Kelemen WL, Fulton EK (2008) Cigarette abstinence impairs memory and metacognition despite administration of 2 mg nicotine gum. Exp Clin Psychopharmacol 16:521–531
Kornell N (2009) Metacognition in humans and animals. Curr Dir Psychol Sci 18:11–15
Kornell N, Son L, Terrace H (2007) Transfer of metacognitive skills and hint seeking in monkeys. Psych Sci 18:64–71
Mazur JE (1988) Choice between small certain and large uncertain reinforcers. Anim Learn Behav 16:199–205
Mazur J (2007) Rats’ choices between one and two delayed reinforcers. Learn Behav 35:169–176
McMahon S, Macpherson K, Roberts WA (2010) Dogs choose a human informant: metacognition in canines. Behav Process 85:293–298
Metcalfe J, Kober H (2005) Self-reflective consciousness and the projectable self. In: Terrace HS, Metcalfe J (eds) The missing link in cognition: origins of self-reflective consciousness. Oxford University Press, New York, pp 57–83
Richards J, Mitchell S, de Wit H, Seiden L (1997) Determination of discount functions in rats with an adjusting-amount procedure. J Exp Anal Behav 67:353–366
Roberts WA, Feeney MC, McMillan N, MacPherson K, Musolino E, Petter M (2009) Dopigeons (Columba livia) study for a test? J Exp Psychol Anim Behav Proc 35:129–142
Roelofs J, Papageorgiou C, Gerber RD, Huibers M, Peeters F, Arntz A (2007) On the links between self-discrepancies, rumination, metacognitions, and symptoms of depression in undergraduates. Behav Res Ther 45:1295–1305
Shepard RN (1961) Application of a trace model to the retention of information in a recognition task. Psychometrika 26:185–203
Shepard RN (1987) Toward a universal law of generalization for psychological science. Science 237:1317–1323
Smith JD (2005) Studies of uncertainty monitoring and metacognition in animals and humans. In: Terrace HS, Metcalfe J (eds) The missing link in cognition: origins of self-reflective consciousness. Oxford University Press, New York, pp 242–271
Smith JD (2009) The study of animal metacognition. Trends Cogn Sci 13:389–396
Smith JD, Beran MJ, Redford JS, Washburn DA (2006) Dissociating uncertainty responses and reinforcement signals in the comparative study of uncertainty monitoring. J Exp Psychol Gen 135:282–297
Smith JD, Beran MJ, Couchman JJ, Coutinho MVC (2008) The comparative study of metacognition: sharper paradigms, safer inferences. Psychon Bull Rev 15:679–691
Smith JD, Redford JS, Beran MJ, Washburn DA (2010) Rhesus monkeys (Macaca mulatta) adaptively monitor uncertainty while multi-tasking. Anim Cogn 13:93–101
Sole LM, Shettleworth SJ, Bennett PJ (2003) Uncertainty in pigeons. Psychon Bull Rev 10:738–745
Son LK, Kornell N (2005) Metaconfidence judgments in rhesus macaques: explicit versus implicit mechanisms. In: Terrace HS, Metcalfe J (eds) The missing link in cognition: origins of self-reflective consciousness. Oxford University Press, New York, pp 296–320
Sutton JE, Shettleworth SJ (2008) Memory without awareness: pigeons do not show metamemory in delayed matching-to-sample. J Exp Psychol Anim Behav Proc 34:266–282
Washburn DA, Gulledge JP, Beran MJ, Smith JD (2010) With his memory magnetically erased, a monkey knows he is uncertain. Biol Lett 6:163–166
White KG (2002) Psychophysics of remembering: the discrimination hypothesis. Curr Dir Psychol Sci 11:141–145
Acknowledgments
We thank Tony Snodgrass for help with programing the simulations. We thank the reviewers of a previous version of the manuscript for insightful criticism. This work was supported by National Institute of Mental Health Grants R01MH64799 and R01MH080052 (to J.D.C).
Conflict of interest
The experiments complied with the current laws of the country in which they were performed. The authors declare that they have no conflict of interest.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Foote, A.L., Crystal, J.D. “Play it Again”: a new method for testing metacognition in animals. Anim Cogn 15, 187–199 (2012). https://doi.org/10.1007/s10071-011-0445-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10071-011-0445-y