Estimating aquifer hydraulic properties using sinusoidal pumping at the Savannah River site, South Carolina, USA

Abstract

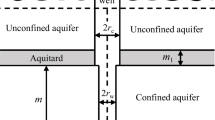
A framework for estimating aquifer hydraulic properties using sinusoidal pumping is presented that (1) derives analytical solutions for confined, leaky, and partially penetrating conditions; (2) compares the analytical solutions with a finite element model; (3) establishes a field protocol for conducting sinusoidal aquifer tests; and (4) estimates aquifer parameters using the analytical solutions. The procedure is demonstrated in one surficial and two confined aquifers containing potentially contaminated water in coastal plain sediments at the Savannah River site, a federal nuclear facility. The analytical solutions compare favorably with finite-element solutions, except immediately adjacent to the pumping well where the assumption of zero borehole radius is not valid. Estimated aquifer properties are consistent with previous studies for the two confined aquifers, but are inconsistent for the surficial aquifer; conventional tests yielded estimates of the specific yield—consistent with an unconfined response—while the shorter-duration sinusoidal perturbations yielded estimates of the storativity—consistent with a confined, elastic response. The approach minimizes investigation-derived wastes, a significant concern where contaminated fluids must be disposed of in an environmentally acceptable manner. An additional advantage is the ability to introduce a signal different from background perturbations, thus easing detection.

Résumé

Une démarche pour estimer les propriétés d'un aquifère à partir d'un débit de pompage à variations sinusoïdales est présentée pour (1) dériver des solutions analytiques pour des conditions captives, en drainance, et de puits incomplet convenant à plusieurs applications pratiques, (2) vérifier les solutions analytiques par rapport à un modèle aux éléments finis, (3) établir un protocole de terrain pour réaliser des essais d'aquifère, et (4) estimer les paramètres de l'aquifère à partir de solutions analytiques. Les solutions analytiques soutiennent bien la comparaison avec les solutions aux éléments finis d'un domaine d'écoulement simulé, sauf dans les zones immédiatement voisines du puits de pompage où l'hypothèse d'un rayon de forage nul n'est pas respectée. La procédure de terrain utilise (1) une chaîne d'acquisition de données programmable que contrôlent des pompes à régime variable qui alternativement injectent et extraient l'eau du forage pour créer une impulsion sinusoïdale, (2) un conteneur mobile, au-dessus du sol qui stocke momentanément l'eau de l'aquifère entre les cycles d'extraction et d'injection, (3) des débitmètres à palettes qui contrôlent les débits d'extraction et d'injection, et (4) des capteurs de pression qui contrôlent les niveaux d'eau dans les forages de pompage et d'observation. La procédure est appliquée à une unité aquifère superficielle et à deux unités captives du site de la rivière Savannah, un site nucléaire fédéral de Caroline du Sud. L'approche sinusoïdale fournit rapidement des estimations des paramètres de l'aquifère en évitant les pertes de temps liées aux études.

Resumen

Se presenta un marco para estimar las propiedades de los acuíferos mediante una tasa de extracción sinusoidal. El método (1) deriva soluciones analíticas para condiciones de acuífero confinado, semiconfinado y de penetración parcial, que son aplicables a muchas situaciones prácticas; (2) verifica las soluciones analíticas con un modelo de elementos finitos; (3) establece un protocolo de campo para ejecutar ensayos hidráulicos; y (4) estima los parámetros del acuífero por medio de las soluciones analíticas. Éstas han sido validadas de forma satisfactoria con soluciones numéricas en un dominio simulado de flujo, exceptuando las áreas adyacentes al pozo de bombeo, para el que la hipótesis de radio nulo no se cumple. El procedimiento de campo utiliza (1) un registrador de datos programable que controla las bombas de velocidad variable que inyectan y extraen agua de forma alternativa desde el sondeo con el fin de crear un estímulo sinusoidal; (2) un contenedor móvil, situado en superficie, que almacena temporalmente el fluido del acuífero durante los ciclos; (3) contadores volumétricos tipo noria que registran las tasas de inyección y extracción; y (4) transductores de presión para observar los niveles del agua en los sondeos de bombeo y control. El procedimiento ha sido verificado en un acuífero superficial y en dos niveles confinados del emplazamiento del río Savannah, en Carolina del Sur (Estados Unidos de América), donde se ubican unas instalaciones nucleares federales. El enfoque sinusoidal permite efectuar estimaciones rápidas de los parámetros del acuífero a la par que elimina residuos derivados de la investigación.

Appendix

This appendix presents derivations for the hydraulic response to sinusoidal pumping in three types of aquifers: fully penetrating wells in confined aquifers, fully penetrating wells in leaky aquifers, and partially penetrating wells in confined aquifers. The approach follows the conventional method of obtaining solutions for constant pumping problems, except that the pumping rate is now treated as a complex coefficient.

The solutions are obtained by first using the Laplace transform to eliminate the time derivative, and then, for the partially penetrating problem, by using the finite Fourier cosine transform to eliminate the derivative with respect to the vertical dimension. Analytical solutions in the transformed domain are then inverse-transformed to provide aquifer responses in time. Alternatively, the inverse-transforms could be performed numerically, if desired.

Derivation of Confined Aquifer Response

The response of a confined aquifer to sinusoidal pumping is obtained by the use of Laplace transforms. The Laplace transform of an arbitrary function f(r,t) with respect to t and p is defined as:

$$ L\left\{ {f(r,t)} \right\} = \bar f(r,p) = \int_o^\infty {e^{ - pt} f(r,t)\,dt} $$

(37)

and has the property that:

$$ L\left\{ {f'(r,t)} \right\} = p\,\bar f(r,p) - f(r,0) $$

(38)

where the prime denotes differentiation with respect to time (Carslaw and Jaeger 1953; Poularikas 1996). Taking the Laplace transform with respect to t and p of Eq. (2), (4), and (5) using Eq. (37) and (38) yields:

$$ {{\partial ^2 \bar s} \over {\partial r^2 }} + {1 \over r}{{\partial \bar s} \over {\partial r}} - {p \over D}\bar s = 0 $$

(39)

$$ \bar s\,(\infty ,p) = 0 $$

(40)

$$ \mathop {\lim }\limits_{r \to 0} \,\,r\,\,{{\partial \bar s} \over {\partial r}} = {{ - \,Q_o } \over {2\pi T}}{1 \over {p - {\bf{i}}\omega }} $$

(41)

Equation (39) is the modified Bessel differential equation of zero order and has the general solution

$$ \bar s(r,p) = A_1 \,K_o \left( {r\;\root \of {{p \over D}} } \right)\,\, + \,\,A_2 \,I_o \left( {r\;\root \of {{p \over D}} } \right) $$

(42)

where I _o and K _o are the zero-order modified Bessel functions of the first and second kind, respectively, and A ₁ and A ₂ are constants. Equation (40) can be used to show that A ₂=0, because I _o→∞ as r→∞.

It can be shown that:

$$ \mathop {\lim }\limits_{u \to 0} \,\,u\,\,{{dK_o (u)} \over {du}} = 1 $$

(43)

because:

$$ {{dK_o (x)} \over {dx}} = K_1 (x) $$

(44)

and:

$$ \mathop {\lim }\limits_{x \to 0} \,\,x\,K_1 (x) = 1 $$

(45)

so that:

$$ A_1 = {{Q_o } \over {2\pi T(p - {\bf{i}}\omega )}} $$

(46)

resulting in:

$$ \bar s(r,p) = {{Q_o } \over {2\pi T(p - {\bf i}\omega )}}K_o \left( {r\;\root \of {{p \over D}} } \right) $$

(47)

Convolution can be used to obtain the inverse Laplace transform of Eq. (47) (Haborak 1999), yielding:

$$ s(r,t) = {Q \over {2\pi T}}\left[ {K_o \left( {r\;\root \of {{{{\bf i}\omega } \over D}} } \right)\,\, - \,\,\int_{\,o}^\infty {{{\lambda \,\,J_o (r\lambda )} \over {{{{\bf i}\omega } \over D} + \lambda ^2 }}\,\,e^{ - ({\bf i}\omega + D\lambda ^2 )\,t} d\lambda } \,} \right] $$

(48)

The first term within the brackets is the steady periodic response, while the second term is an initial transient response. If the second term is important, then a brief period may be necessary to allow the initial transient to dissipate. The initial transient results from quiescent conditions at the beginning of the test, in which the initial water levels are assumed to be static, rather than at steady periodic conditions.

Derivation of Leaky Aquifer Response

The response of a confined aquifer to sinusoidal pumping is obtained by taking the Laplace transform of the governing equation, yielding:

$$ {{\partial ^2 \bar s} \over {\partial r^2 }}\,\, + \,\,{1 \over r}\,\,{{\partial \bar s} \over {\partial r}}\,\, - \,\,\left( {{1 \over {B^2 }} + {p \over D}} \right)\,\,\bar s = 0 $$

(49)

$$ \bar s(\infty ,p) = 0 $$

(50)

$$ \mathop {\lim }\limits_{r \to 0} \,\,r\,\,{{\partial \bar s} \over {\partial r}} = {{ - Q_o } \over {2\,\pi \,\,T}}\,\,{1 \over {p - {\bf{i}}\omega }} $$

(51)

Equation (49) is the modified Bessel differential equation of zero order and has the general solution:

$$ \bar s(r,p) = A_1 \,\,K_o \left( {r\;\root \of {{p \over D} + {1 \over {B^2 }}} } \right)\,\, + \,\,A_2 \,\,I_o \left( {r\;\root \of {{p \over D} + {1 \over {B^2 }}} } \right) $$

(52)

which reduces to:

$$ s_l (r,p) = {{ - Q_o } \over {2\,\pi \,\,\,T(p - {\bf i}\omega )}}\,\,K_o \left( {r\;\root \of {{p \over D} + {1 \over {B^2 }}} } \right) $$

(53)

because A ₂=0. Convolution can be used to obtain the inverse Laplace transform (Haborak 1999), resulting in:

$$ s(r,t) = {Q \over {2\pi T}}\left[ {K_o \left( {r\;\root \of {{{{\bf i}\omega } \over D} + {1 \over {B^2 }}} } \right) - \int_o^\infty {{{\lambda \,J_o (r\lambda )} \over {{{{\bf i}\omega } \over D} + {1 \over {B^2 }} + \lambda ^2 }}e^{ - ({\bf i}\omega + {D \over {B^2 }} + D\lambda ^2 )\,\,\,t} d\lambda } } \right] $$

(54)

The first term inside the brackets is again the steady periodic response, while the second term is the transient response to initial conditions.

Response in Partially Penetrating Wells

The derivation of the solution to the partially penetrating boundary value problem is found by first obtaining the Laplace transform with respect to t of Eqs. (17) and (19), (20), (21), and (22):

$$ {{\partial ^2 \bar s} \over {\partial r^2 }} + {1 \over r}{{\partial \bar s} \over {\partial r}} + {{\partial ^2 \bar s} \over {\partial z^2 }} - {p \over D}\bar s = 0 $$

(55)

$$ \bar s(\infty ,z,p) = 0 $$

(56)

$$ \left. {{{\partial \bar s} \over {\partial z}}} \right|_{z = 0} = 0 $$

(57)

$$ \left. {{{\partial \bar s} \over {\partial z}}} \right|_{z = m} = 0 $$

(58)

$$ \mathop {\lim }\limits_{r \to 0} \,\,r\,\,{{\partial \bar s} \over {\partial r}} = \left\{ {\matrix{ 0 & {0 \le z < d} \cr {{{ - \,\,Q_o } \over {2\pi \,\,K(l - d)\,\,(p - {\bf{i}}\omega )}}} & {d \le z \le l} \cr 0 & {l < z \le m} \cr } } \right. $$

(59)

Given a function defined in the interval 0≤z≤m, the finite Fourier cosine transform with respect to z and m is defined as:

$$ F_c \left\{ {f(r,z,t)} \right\} = f_c (r,n,t) = \int_o^m {f(r,z,t)\,\,cos{{n\pi z} \over m}\,\,dz} $$

(60)

where n=0, 1, 2,.... The transform has the property that:

$$ F_c \left\{ {f''(r,z,t)} \right\} = - \left( {{{n\pi } \over b}} \right)^2 f_c (r,n,t) + ( - 1)^n f'\,(r,m,t) - f'(r,0,t) $$

(61)

where the prime denotes differentiation with respect to z (Miles 1971; Pinkus and Zafrany 1977; Sneddon 1972).

Taking the finite Fourier cosine transform from 0 to m of Eq. (55) with respect to z and n yields:

$$ {{\partial ^2 \bar s_c } \over {\partial r^2 }} + {1 \over r}{{\partial \bar s_c } \over {\partial r}} - {{p\bar s_c } \over D} - \left[ {{{n\pi } \over m}} \right]^2 \bar s_c + ( - 1)^n f'(r,m,p) - f'(r,0,p) = 0 $$

(62)

which, upon substitution of Eqs. (57) and (58), yields:

$$ {{\partial ^2 \bar s_c } \over {\partial r^2 }} + {1 \over r}{{\partial \bar s_c } \over {\partial r}} - \left[ {{p \over D} + \left( {{{n\pi } \over m}} \right)^2 } \right]\bar s_c = 0 $$

(63)

Equation (63) is the modified Bessel differential equation of zero order and has the general solution:

$$ \bar s_c (r,n,p) = A_{1,n} K_o \left[ {r\;\root \of {{p \over D} + \left( {{{n\pi } \over m}} \right)^2 } } \right] + A_{2,n} I_o \left[ {r\;\root \of {{p \over D} + \left( {{{n\pi } \over m}} \right)^2 } } \right] $$

(64)

Equations (56) and (59) become:

$$ \bar s_c (\infty ,n,p) = 0 $$

(65)

$$ \mathop {\lim }\limits_{r \to 0} \,\,r\,{{\partial \bar s_c } \over {\partial r}} = \int_{\,d}^{\,l} {{{ - Q_o } \over {2\pi K(l - d)(p - {\bf{i}}\omega )}}cos{{n\pi z} \over m}dz} $$

(66)

The integral of this function for n=0 is:

$$ \mathop {\lim }\limits_{r \to 0} \,\,r\,{{\partial \bar s_c } \over {\partial r}} = {{ - Q_o } \over {2\,\pi \,\,K(p - {\bf{i}}\omega )}} $$

(67)

$$ \mathop {\lim }\limits_{r \to 0} r{{\partial \bar s_c } \over {\partial r}} = {{ - \,Q_o } \over {2\,\pi \,\,K\,(l - d)\,(p - {\bf{i}}\omega )}}\,\,{m \over {n\pi }}\,\,\left[ {sin{{n\pi l} \over m} - sin{{n\pi d} \over m}} \right] $$

(68)

Simplification yields:

$$ \bar s_c (r,n,p) = {{Q_o } \over {2\,\pi \,\,K\,(p - {\bf i}\omega )}}\,\,K_o \left[ {r\;\root \of {{p \over D} + \left( {{{n\pi } \over m}} \right)^2 } } \right] $$

(69)

and for n=0. Using Equation (68):

$$ A_{1,n} = {{Q_o } \over {2\,\pi \,\,K\,(l - d)\,\,(p - {\bf{i}}\omega )}}\,\,{m \over {n\pi }}\,\,\left[ {sin{{n\pi l} \over m} - sin{{n\pi d} \over m}} \right] $$

(70)

Therefore:

$$ \bar s_c (r,n,p) = {{Q_o } \over {2\,\pi \,\,K\,(l - d)\,(p - {\bf i}\omega )}}\,\,{m \over {n\pi }}\,\,\left[ {sin{{n\pi l} \over m} - sin{{n\pi d} \over m}} \right]K_o \left[ {r\;\root \of {{p \over D} + \left( {{{n\pi } \over m}} \right)^2 } } \right] $$

(71)

for n=1, 2, 3,.... The inverse Fourier cosine transform is given by:

$$ \bar s(r,z,p) = {1 \over m}\bar s_c (r,0,p)\,\, + \,\,{2 \over m}\int\limits_{n = 1}^\infty {\bar s_c (r,n,p)\,\,cos{{n\pi z} \over m}} $$

(72)

Inverting Eqs. (69) and (71) yields:

$$ \eqalign{ & \bar s(r,n,p) = {{Q_o } \over {2\,\pi \,\,T\,(p - {\bf i}\omega )}}\,\,\left\{ {K_o \left[ {r\;\root \of {{p \over D} + \left( {{{n\pi } \over m}} \right)^2 } } \right]} \right. \cr & \left. { + {{2m} \over {\pi \,(l - d)}}\int\limits_{n = 1}^\infty {\,\,{1 \over n}\,\,\,\,\left[ {sin{{n\pi l} \over m} - sin{{n\pi d} \over m}} \right]\,\,K_o \left[ {r\;\root \of {{p \over D} + \left( {{{n\pi } \over m}} \right)^2 } } \right]\,\,cos{{n\pi z} \over m}} } \right\} \cr} $$

(73)

Convolution can be used to obtain the inverse Laplace transform:

$$ s(r,z,t) = {Q \over {2\pi T}}\left[ {C_1 + C_2 - C_3 - C_4 } \right] $$

(74)

where:

$$ C_1 = K_o \left[ {r\;\root \of {{{{\bf i}\omega } \over D}} } \right] $$

(75)

$$ C_2 = {{2m} \over {\pi (l - d)}}\,\,\int\limits_{n = 1}^\infty {\,\,{1 \over n}\,\,\left[ {sin{{n\pi l} \over m} - sin{{n\pi d} \over m}} \right]\,\,K_o \left[ {r\;\root \of {{{{\bf i}\omega } \over D} + \left( {{{n\pi } \over m}} \right)^2 } } \right]\,\,cos{{n\pi z} \over m}} $$

(76)

$$ C_3 = \int_o^\infty {{{\lambda J_o (r\lambda )} \over {{{{\bf{i}}\omega } \over D} + \lambda ^2 }}\,\,e^{ - ({\bf{i}}\omega + D\lambda ^2 )t} \,\,d\lambda } $$

(77)

$$ C_4 = {{2m} \over {\pi (l - d)}}\int\limits_{n = 1}^\infty {\,{1 \over n}\,\,\left[ {sin{{n\pi l} \over m} - sin{{n\pi d} \over m}} \right]\,\,cos{{n\pi z} \over m}} \,\,\int_o^\infty {{{\lambda J_o (r\lambda )} \over {{{{\bf{i}}\omega } \over D} + \lambda ^2 + \left[ {{{n\pi } \over m}} \right]^2 }}\,\,e^{ - \left( {{\bf{i}}\omega + D\lambda ^2 + \left[ {{{n\pi D} \over m}} \right]^2 } \right)\,t} \,\,d\lambda } $$

(78)

The integral terms in C ₃ and C ₄ are transient responses to initial conditions. The steady periodic response is, therefore:

$$ s(r,z,t) = {Q \over {2\,\pi \,\,T}}\,\,\left[ {C_1 + C_2 } \right] $$

(79)

The steady periodic response in an observation well screened from a depth of l' to d' is the average value of the drawdown over that interval, and is given by:

$$ s(r,l',d',t) = {Q \over {2\,\pi \,\,T\,(l' - d')}}\,\,\int_{d'}^{l'} {\,\left[ {C_1 + C_2 } \right]\,\,dz} $$

(80)

which is equal to:

$$ \eqalign{ & s(r,l',d',t) = {Q \over {2\pi T}}\,\,\left\{ {K_o \left[ {r\;\root \of {{{{\bf i}\omega } \over D}} } \right]\,\, + \,\,{{2m^2 } \over {\pi ^2 \,\,(d' - l')\,\,(l - d)}}} \right. \cr & \left. {\int\limits_{n = 1}^\infty {{1 \over {n^2 }}\left[ {sin{{n\pi l} \over m} - sin{{n\pi d} \over m}} \right]} \,K_o \left[ {r\;\root \of {{{{\bf i}\omega } \over D} + \left( {{{n\pi } \over m}} \right)^2 } } \right]\left[ {sin{{n\pi l'} \over m} - sin{{n\pi d'} \over m}} \right]} \right\} \cr} $$

(81)