Skip to main content
SpringerLink
Log in

Paradox of a particle’s trajectory moving on a string

  • Original
  • Published:
Archive of Applied Mechanics Aims and scope Submit manuscript

Abstract

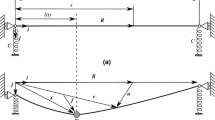
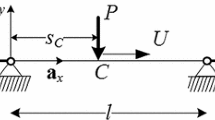
This paper deals with the paradoxical properties of the solution of string vibration under a moving mass. The solutions published to date are not simple enough and cannot be applied to investigations in the entire range of mass speeds, including the overcritical range. We propose a formulation of the problem that allows us to reduce the problem to a second-order matrix differential equation. Its solution is characteristic of all features of the critical, subcritical, and overcritical motion. Results exhibit discontinuity of the mass trajectory at the end support point, which has not been previously reported in the literature. The closed solution in the case of a massless string is analyzed and the discontinuity is proved. Numerical results obtained for an inertial string demonstrate similar features. Small vibrations are analyzed, which is why the effect discussed in the paper is of purely mathematical interest. However, the phenomenon results in complexity in discrete solutions.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. Panovko, J.: Historical outline of the theory of dynamic influence of moving load (in Russian). Eng. Acad. Air Forces 17, 8–38 (1948)

    Google Scholar 

  2. Jakushev, N.Z.: Certain problems of dynamics of the beam under moving load (in Russian). Kazan Univ. 12, 199–220 (1974)

    Google Scholar 

  3. Dmitrijev, A.S.: The analysis of solutions of problems with lateral oscillatory vibrations of various beam structures under the motion of non spring point load (in Russian). Mach. Dyn. Problems 24, 18– (1985)

    Google Scholar 

  4. Saller, H.: Einfluss bewegter Last auf Eisenbahnoberbau und Brücken. Kreidels Verlag, Berlin und Wiesbaden (1921)

    Google Scholar 

  5. Inglis, C.E.: A Mathematical Treatise on Vibrations in Railway Bridges. Cambridge University Press, London (1934)

    MATH  Google Scholar 

  6. Schallenkamp, A.: Schwingungen von Trägern bei bewegten Lasten. Arch. Appl. Mech. (Ingenieur Archiv) 8(3), 182–198 (1937)

    MATH  Google Scholar 

  7. Bolotin, W.W.: On the influence of moving load on bridges (in Russian). Rep. Moscow Univ. Railway Transp. MIIT 74, 269–296 (1950)

    Google Scholar 

  8. Bolotin, W.W.: Problems of bridge vibration under the action of the moving load (in Russian). Izvestiya AN SSSR, Mekh. Mashinostroenie 4, 109–115 (1961)

    Google Scholar 

  9. Morgaevskii, A.B.: Critical velocities calculation in the case of a beam under moving load (in Russian). Mekh. Mashinostroenie, Izvestiya AN SSSR, OTN 3, 176–178 (1959)

    Google Scholar 

  10. Szcześniak, W.: Inertial moving loads on beams (in Polish). Scientific Reports, Technical University of Warsaw, Civil Engineering 112 (1990)

  11. Ting, E.C., Genin, J., Ginsberg, J.H.: A general algorithm for moving mass problems. J. Sound Vib. 33(1), 49–58 (1974)

    Article  MATH  Google Scholar 

  12. Smith, C.E.: Motion of a stretched string carrying a moving mass particle. J. Appl. Mech. 31(1), 29–37 (1964)

    MATH  Google Scholar 

  13. Frỳba, L.: Vibrations of solids and structures under moving loads. Academia, Prague (1972)

    Google Scholar 

  14. Wu, J.-J.: Dynamic analysis of an inclined beam due to moving loads. J. Sound Vib. 288, 107–131 (2005)

    Article  Google Scholar 

  15. Metrikine, A.V., Verichev, S.N.: Instability of vibration of a moving oscillator on a flexibly supported Timoshenko beam. Arch. Appl. Mech. 71(9), 613–624 (2001)

    Article  MATH  Google Scholar 

  16. Pesterev, A.V., Bergman, L.A., Tan, C.A., Tsao, T.-C., Yang, B.: On asymptotics of thesolution of the moving oscillator problem. J. Sound Vib. 260, 519–536 (2003)

    Article  Google Scholar 

  17. Biondi, B., Muscolino, G.: New improved series expansion for solving the moving oscillator problem. J. Sound Vib. 281, 99–117 (2005)

    Article  Google Scholar 

  18. Andrianov, I.V., Awrejcewicz, J.: Dynamics of a string moving with time-varying speed. J. Sound Vib. 292, 935–940 (2006)

    Article  MathSciNet  Google Scholar 

  19. Michaltsos, G.T.: Dynamic behaviour of a single-span beam subjected to loads moving with variable speeds. J. Sound Vibr. 258(2), 359–372 (2002)

    Article  Google Scholar 

  20. Gavrilov, S.N., Indeitsev, D.A.: The evolution of a trapped mode of oscillations in a string on an elastic foundation G moving inertial inclusion system. J. Appl. Math. Mech. 66(5), 852–833 (2002)

    Article  MathSciNet  Google Scholar 

  21. Gavrilov, S.N.: The effective mass of a point mass moving along a string on a Winkler foundation. J. Appl. Math. Mech. 70(4), 641–649 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  22. Rodeman, R., Longcope, D.B., Shampine, L.F.: Response of a string to an accelerating mass. J. Appl. Mech. 98(4), 675–680 (1976)

    MATH  Google Scholar 

  23. Kaplunov, Y.D.: The torsional oscillations of a rod on a deformable foundation under the action of a moving inertial load (in Russian). Izv Akad Nauk SSSR, MTT 6, 174–177 (1986)

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Institute of Fundamental Technological Research, Polish Academy of Sciences, Świętokrzyska 21, 00-049, Warsaw, Poland

    Bartłomiej Dyniewicz & Czesław I. Bajer

Authors
  1. Bartłomiej Dyniewicz
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Czesław I. Bajer
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Czesław I. Bajer.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Dyniewicz, B., Bajer, C.I. Paradox of a particle’s trajectory moving on a string. Arch Appl Mech 79, 213–223 (2009). https://doi.org/10.1007/s00419-008-0222-9

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00419-008-0222-9

Keywords

Search

Navigation