ENSO-driven energy budget perturbations in observations and CMIP models

Abstract

Various observation-based datasets are employed to robustly quantify changes in ocean heat content (OHC), anomalous ocean–atmosphere energy exchanges and atmospheric energy transports during El Niño-Southern Oscillation (ENSO). These results are used as a benchmark to evaluate the energy pathways during ENSO as simulated by coupled climate model runs from the CMIP3 and CMIP5 archives. The models are able to qualitatively reproduce observed patterns of ENSO-related energy budget variability to some degree, but key aspects are seriously biased. Area-averaged tropical Pacific OHC variability associated with ENSO is greatly underestimated by all models because of strongly biased responses of net radiation at top-of-the-atmosphere to ENSO. The latter are related to biases of mean convective activity in the models and project on surface energy fluxes in the eastern Pacific Intertropical Convergence Zone region. Moreover, models underestimate horizontal and vertical OHC redistribution in association with the generally too weak Bjerknes feedback, leading to a modeled ENSO affecting a too shallow layer of the Pacific. Vertical links between SST and OHC variability are too weak even in models driven with observed winds, indicating shortcomings of the ocean models. Furthermore, modeled teleconnections as measured by tropical Atlantic OHC variability are too weak and the tropical zonal mean ENSO signal is strongly underestimated or even completely missing in most of the considered models. Results suggest that attempts to infer insight about climate sensitivity from ENSO-related variability are likely to be hampered by biases in ENSO in CMIP simulations that do not bear a clear link to future changes.

1 Introduction

El Niño-Southern Oscillation (ENSO) is the preeminent mode of global internal climate variability. It leads to strong anomalies of the atmosphere–ocean energy budget not only in the tropical Pacific Ocean, but also on a global scale. However, important details remain unclear, especially with respect to the buildup, redistribution and discharge of heat within the ocean that contribute to the time scale of ENSO events and their predictability. The ability of models to properly replicate related processes is also an open question. These are the core topics addressed in this paper.

One prevailing theory of ENSO is the recharge-discharge hypothesis by Wyrtki (1975) updated by Suarez and Schopf (1988) and Jin (1997). It is centered on a build up of ocean heat in the tropical western Pacific in the cool phase, and then in the course of the El Niño event, the heat is moved across the Pacific and then polewards within the ocean. This process involves lateral and vertical redistribution of heat within the basin (Roemmich and Gilson 2011), increasing the area of warm surface water leading to heat loss to the atmosphere primarily by enhanced evaporation. The latter cools the ocean and moistens the atmosphere, invigorating convection, storms and teleconnections, dispersing energy and leading to a mini global warming in the sense of an increase in global mean temperature (e.g., Trenberth et al. 2002a).

Mayer et al. (2014) showed that the quality of current ocean and atmosphere reanalyses is sufficient to quantitatively describe interannual variability of ENSO and the tropical coupled atmosphere–ocean energy budget. Specifically, tropical Pacific (area-averaged over 30N–30S) ocean heat content (OHC) variability associated with ENSO is mainly governed by surface energy exchanges rather than lateral ocean energy divergence. The latter nevertheless plays an important role in redistributing OHC within the basin (Roemmich and Gilson 2011). Secondary contributions stem from variability of Indonesian Throughflow heat transport while poleward ocean heat export variability across 30N and 30S in association with ENSO is negligible within uncertainty bounds. Furthermore, Mayer et al. (2014) demonstrated that a large fraction of energy released from the tropical Pacific during El Niño is exported laterally by the atmosphere, while energy exchanges at top-of-atmosphere (TOA) are relatively small. The lateral divergence of energy by the atmosphere (DIVFA) over the tropical Atlantic and Indian Oceans are anti-correlated with Pacific DIVFA. That is, divergence of atmospheric energy over the Pacific is compensated for to a large degree by convergence of energy over the Atlantic and Indian Oceans and these are tightly connected to surface fluxes. Variability in OHC in association with ENSO and teleconnections to the tropical Atlantic are well-known (e.g. Enfield and Mayer 1997), but Mayer et al. (2014) were able to bring these aspects together into a quantitatively consistent energy budget framework (see Fig. 1 for a schematic of the described energy flows).

Fig. 1

Schematic of energy budget anomalies associated with ENSO as described in Sect. 1, based on a regression of the fields onto N3.4. Rad_TOA denotes net radiation at TOA, F_S net surface energy flux, ITF the Indonesian Throughflow and OHCT the tendency of ocean heat content. Reproduced from Fig. 6 in Mayer et al. (2014). ©American Meteorological Society. Used with permission

This new ability to document energy budget anomalies through the course of ENSO events motivates an assessment of coupled ENSO simulations presented here. Model runs from the Coupled Model Intercomparison Project Phase 5 (CMIP5) still exhibit mean state biases in the tropics, such as the mean depth and slope of the equatorial thermocline, an excessive Pacific cold tongue, and the zonal sea surface temperature (SST) gradient in the equatorial Atlantic (Flato et al. 2013). Recent studies have assessed ENSO in coupled models from various perspectives (e.g., Guilyardi et al. 2012) and energy budget diagnostics have been employed in order to understand the contrasting projections of ENSO characteristics (e.g., DiNezio et al. 2012). Some of the documented shortcomings can be attributed to the biased mean state (Bellenger et al. 2014). Overall, improvements from CMIP3 to CMIP5 regarding mean state biases and ENSO characteristics are found to be modest (Flato et al. 2013).

Here, we build on the results from Mayer et al. (2014) to investigate the fidelity of ENSO-related energy budget variability in CMIP historical model runs with an emphasis on both the characteristics of ENSO in the Pacific Ocean and in remote tropical ocean basins. We show that the pathways of energy through the ENSO cycle are systematically biased in the models in key respects.

Section 2 discusses the datasets and methods used to explore the atmospheric and oceanic budget variability in observations and models. The ratio of OHC and SST standard deviations in the Niño 3.4 region as a measure of strength of the vertical link between the surface and deeper layers of the ocean is assessed in Sect. 3.1. One key feature of ENSO, the recharge and discharge of tropical Pacific basin-averaged OHC, is found to be drastically underestimated by models, as detailed in Sects. 3.2–3.4. In addition, ENSO teleconnections to the Atlantic and the zonal mean ENSO signal are found to be weaker in the models when compared to reanalyses (Sects. 3.5–3.6). Reasons for these biases are hypothesized to arise, at least partly, from errors in the climatological mean state of the models.

2 Methods and data

Diagnostics presented in this paper are based on a vertically integrated energy budget framework. Vertical integration reduces the total energy budget of the atmosphere to

$${\text{F}}_{\text{S}} = {\text{Rad}}_{\text{TOA}} - {\text{AET }} - {\text{ DIVFA}},$$

(1)

where F_S denotes net surface energy flux, Rad_TOA net radiation at TOA, AET the vertically integrated tendency of atmospheric energy, and DIVFA the divergence of vertically integrated lateral atmospheric transport of moist static plus kinetic energy. Anomalies of AET in the tropics are small across monthly and longer timescales. The vertically integrated oceanic energy budget is as follows:

$${\text{F}}_{\text{S}} = {\text{OHCT}} + {\text{DIVFO}},$$

(2)

where OHCT is the tendency of OHC and DIVFO the divergence of vertically integrated horizontal ocean heat transport. Note that all vertical fluxes are defined as positive downward unless otherwise stated. Please note that all terms in Eqs. (1) and (2) will be considered as fields or area-averages over specific regions throughout this paper, depending on the respective diagnostics.

We employ a representative subset of 14 fully coupled historical runs from the CMIP5 multi-model ensemble (Table 1). Monthly averages of F_S, Rad_TOA, atmospheric total energy, and OHC are computed directly from model output. Fields of AET and OHCT are computed from centered differences of atmospheric total energy and OHC, respectively, as no snapshots of these fields are available. However, as all results presented here are temporally smoothed, the introduced inconsistencies are negligible. Fields of DIVFA and DIVFO from models are computed as residuals from the remaining terms in Eqs. (1) and (2).

Table 1 Modeling centers as well as names of CMIP3 and CMIP5 models employed in this study

In addition to the coupled CMIP5 runs, we employ OHC and SST data from one run of the ocean component of the CCSM4 model forced by version 2 forcing for coordinated ocean-ice reference experiments (CORE2, see Large and Yeager 2009), covering 1979–2007. We also study data from the output of coupled 20th century runs (20CM3) of a 16-model ensemble of the World Climate Research Programme CMIP3 multi-model dataset (Table 1) to document the progress made from CMIP3 to CMIP5. To obtain an observation-based reference estimate of energy exchanges associated with ENSO, we use various satellite data sets, atmospheric reanalyses, and ocean reanalyses as outlined below.

Satellite observations of radiation at TOA from Clouds and the Earth’s Radiant Energy System (CERES; Loeb et al. 2009) are employed for the period 2000/03–2013/02. In order to extend data availability backwards in time, we additionally use Rad_TOA estimates from the University of Reading (UR; Allan et al. 2014) covering 1985–2013. This is a synthesized data set of adjusted Rad_TOA data from European Centre for Medium-Range Weather Forecasts Interim Re-Analysis (ERA-Interim, hereafter ERA-I; Dee et al. 2011) for the period before 2000/03 and CERES data afterwards.

Mass consistent fields of the divergence of atmospheric energy transports and AET are computed from ERA-I and Modern-Era Retrospective Analysis for Research and Applications (MERRA; Rienecker et al. 2011) using the methods described in Mayer and Haimberger (2012) and Mayer et al. (2013), respectively. Net surface flux is computed indirectly from various combinations of Rad_TOA, DIVFA, and AET. Turbulent surface flux and 10 m wind speed data are taken from the Objectively Analyzed Air-sea Fluxes Project (OAFlux; Jin and Weller 2008) and also from ERA-I. Precipitation data is taken from Global Precipitation Climatology Project (GPCP, Huffman et al. 2009) and ERA-I.

OHC and its tendency is computed using output from Ocean Reanalysis System 4 (ORAS4; Balmaseda et al. 2012), the Hadley Centre EN4 (HEN4; Good et al. 2013) data set, and an ocean temperature data set from the Japanese Meteorological Agency (JMA; Ishii and Kimoto 2009). While ORAS4 employs an ocean model for data assimilation, the HEN4 and JMA data sets represent objective analyses based solely on in situ measurements of the ocean. The divergence of ocean heat transports (DIVFO) is estimated directly from ORAS4 ocean currents and temperature data, covering 1979–2012; see Mayer et al. (2014) for a more detailed discussion of OHC and DIVFO computation from ocean reanalyses.

Data coverage in the world ocean has improved significantly since the early 2000s with the introduction of Argo (a global array of currently more than 3800 temperature and salinity profiling floats). Tropical Pacific OHC is nevertheless well constrained from 1992 onward when satellite altimetry was introduced, and in situ observations of the tropical Pacific subsurface ocean were available from the Tropical Atmosphere Ocean (TAO) array much earlier than 1994, when the array finally was completed. Hence, quality of tropical Pacific OHC estimates is limited before 1992 but as will be shown results do not change much when extending the study period back to the 1980s and are far more robust as two additional strong El Niño events are covered. Moreover, both the amount of ocean temperature measurements as well as the signal of ENSO in OHC decreases with depth (Mayer et al. 2014). Thus, we primarily employ ocean data covering the period 1979–2013 (JMA data covers 1979–2012) integrating not deeper than 700 m. However, to corroborate our findings also with results from the data-rich period after 1992, results will also be given with respect to the 1992–2013 period, where appropriate.

In order to obtain results consistent with the employed ocean data, we use atmospheric data covering also 1979–2013 and give results for 1992–2013 whenever appropriate. For Rad_TOA, results from CERES for the short period from 2000/03 onward will also be given.

For the assessment of outgoing longwave radiation (OLR, positive upward) and absorbed solar radiation (ASR) in Sect. 3.3, a long homogeneous OLR series is composited from Advanced Very High Resolution Radiometer (AVHRR; Liebmann 1996) data before 2000/03 and CERES data afterward. We try to avoid ERA-I shortwave radiation data as much as possible as it lacks variability associated with volcanic eruptions (Dee et al. 2011) and it is known to be inhomogeneous in time especially in the late 2000s (Trenberth et al. 2015). Thus we employ CERES data of ASR for 2000/03 onward and compute ASR for 1985–2000 as a residual from the UR Rad_TOA and the AVHRR OLR data. ERA-I ASR data is used only for the short period from 1979 to 1984 to cover the strong signals associated with the 1982/83 El Niño.

All fields and series presented here represent detrended monthly anomalies with the annual cycle removed and a 13-point time filter applied (Trenberth et al. 2007). For monthly data the half-amplitude point of this filter is about a 12-month period. For basin-wide diagnostics we choose domains bounded by 30N and 30S, as Mayer et al. (2014) have shown with reanalysis data that the response of area-averaged poleward ocean heat transports to ENSO is small, i.e. net surface energy flux and OHC changes balance each other when averaged over this domain.

3 Results

3.1 SST and OHC variability in the Niño 3.4 region

The Niño 3.4 SST anomaly index (170W–120W, 5S–5N, from now N3.4) is widely used as a proxy for the ENSO state. Although patterns of ENSO-related SST anomalies in climate model simulations are different from those observed, N3.4 is still widely used for benchmarking climate models (Flato et al. 2013). Moreover, when assessing ENSO characteristics such as periodicity and average strength in (climate) models, usually the N3.4 index series is used, e.g. by means of spectral analysis or variance estimation (e.g., Bellenger et al. 2014).

El Niño (La Niña) events are associated with anomalously warm (cold) subsurface waters and anomalously deep (shallow) thermocline depths in the central and eastern equatorial Pacific (Trenberth et al. 2002a). As a first diagnostic, we investigate the strength of the relationship between SST and OHC for various layers by comparing the temporal standard deviation of the N3.4 series from the respective datasets to the temporal standard deviation of OHC of the upper 100 m (Fig. 2a) and the upper 700 m (Fig. 2c) of the ocean averaged over the same area as the N3.4 SST index. The standard deviation of N3.4 as estimated from observations (as used in ERA-I and ORAS4) is 0.8 K (based on the 1979–2013 period), and there is a wide range of N3.4 standard deviations in the CMIP5 models, ranging from about 0.5 K to nearly 1.3 K. The standard deviation of OHC from the surface to 100 m (OHC100) from the models scales approximately linearly with N3.4 variability, with OHC100 standard deviations ranging from about 1.7 × 10⁸ J m⁻² to about 5.5 × 10⁸ J m⁻², and the temporal correlation between N3.4 and OHC100 is very high in all datasets with correlation coefficients generally exceeding 0.92 (except for GISS-E2-R with r = 0.87). Note that Niño 3.4 SSTs are in phase with OHC in the Niño 3.4 region as opposed to results for the Pacific zonal mean OHC (Meinen and McPhaden 2000). This indicates that the variability of OHC100 in the N3.4 region is directly related to SSTs and thus the simulated magnitude of ENSO (Fig. 2a). Nonetheless, the standard deviation of OHC100 from ORAS4 (4.5 × 10⁸ J m⁻²) suggests that the strong observed relationship between SSTs, winds and OHC is simulated somewhat too weakly in CMIP5 simulations.

Fig. 2

Niño 3.4 index standard deviation versus the temporal standard deviations of a OHC100 and c OHC700 averaged over the N3.4 region from ORAS4 (1979–2013 and 1992–2013), HEN4 (1992–2013), JMA (1992–2012) and CMIP5 models; Fraction of the standard deviations of b OHC100 and d OHC700 in the N3.4 region and N3.4 index standard deviations. Boxes mark the inner quartiles and whiskers mark the 2.5 and 97.5 % percentiles, respectively; uncertainties are estimated with a block bootstrap method (length of the blocks is set to 6 months); Color code for (b) and (d) is the same as for (a) and (c)

Figure 2b presents the ratio of temporal OHC100 standard deviations and the respective N3.4 standard deviation (RSD100) computed for all considered datasets as a measure of the strength of the link between SST and subsurface ocean variability. The value for ORAS4 is 5.6 (5.1, 6.2) × 10⁸ J m⁻² K⁻¹ for the 1979–2013 period (values in brackets denote 95 % confidence intervals). A very similar result is obtained from ORAS4, HEN4, and JMA for the data-rich period 1992–2013 and also the Argo period (see Table 2). All considered models exhibit a quite uniformly lower RSD100, with the GFDL-ESM2M model showing the highest RSD100 of all models (4.3 (4.1, 4.4) × 10⁸ J m⁻² K⁻¹, 24 % low compared to ORAS4). The GISS-E2-R model shows the lowest RSD100 with 3.3 (3.2, 3.5) × 10⁸ J m⁻² K⁻¹ (40 % low compared to ORAS4; see Table 2 for multi-model means).

Table 2 Fractions of standard deviations of OHC100/OHC700 and SST anomalies averaged over the N3.4 region from observation-based data sets for different periods as well as CMIP multi-model mean results; Values in brackets denote 95 % confidence intervals as estimated from a block bootstrap method

The CORE2 run behaves similar to the coupled runs. It exhibits a quite realistic N3.4 standard deviation (0.9 K), but its OHC100 standard deviation is too low (3.6 × 10⁸ J m⁻²), yielding a RSD100 of 4.2 (3.8, 4.5) × 10⁸ J m⁻² K⁻¹, a very similar value to the coupled runs, while the ORAS4 RSD100 for the 1979–2007 period is 5.4 (5.0, 6.1) × 10⁸ J m⁻² K⁻¹.

The standard deviation of OHC from the surface to 700 m (OHC700) in the CMIP5 models also scales approximately linearly with N3.4 variability, ranging from about 2.6 × 10⁸ J m⁻² to about 10.0 × 10⁸ J m⁻² (see Fig. 2c). The variability of OHC700 from ORAS4 (9.3 × 10⁸ J m⁻²) ranks second among all considered data sets, while its N3.4 variability ranks in the middle of all considered models. For ORAS4, the ratio of OHC700 and N3.4 standard deviations (RSD700) is about 11.7 (10.1, 13.7) × 10⁸ J m⁻² K⁻¹ (Fig. 2d), a robust value across different periods and other observation-based data sets (see Table 2). The RSD700 of all models are too low by 33–55 % (CSIRO-Mk3-6-0: 7.9 × 10⁸ J m⁻² K⁻¹, CanESM2: 5.2 × 10⁸ J m⁻² K⁻¹) when compared to ORAS4 in the 1979–2013 period. As for OHC100, the CORE2 run (RSD700 is 7.8 × 10⁸ J m⁻² K⁻¹) agrees well with the coupled runs rather than with the reanalyses. It is noted that while the correlation of OHC700 and N3.4 is still relatively high in ORAS4 (r = 0.8) and most models, the correlation drops below 0.5 in some models (GISS-E2-R, ACCESS1-0, ACCESS1-3), indicating a too shallow OHC variability compared with ENSO strength and/or relatively high variability unrelated to ENSO in these models.

When the same diagnostic for the CMIP3 model ensemble (see supplements S1 for scatter plots) is computed, the range of standard deviations of both N3.4 (0.2–1.4 K) and OHC100 (0.8–5.9 × 10⁸ J m²) is large compared to CMIP5. The ratio of standard deviations for the CMIP3 models range from 3.3 to 4.5 × 10⁸ J m⁻² K⁻¹ for OHC100 and from 4.3 × 10⁸ to 8.2 × 10⁸ J m⁻² K⁻¹ for OHC700. The GISS-E-R model is an outlier showing a higher RSD700 than observed, but this is probably due to its extremely low N3.4 standard deviation (<0.2 K).

Model results for both RSD100 and RSD700 are similar when computed for shorter subperiods (34 years) of the respective full series (not shown). The most noticeable difference between the results from the shortened and the full periods are the larger error bars due to the higher sampling uncertainty associated with the shorter time series. Thus, at least in the N3.4 region, the differences described above are not due to internal low-frequency variability in the models.

Most of the SST and the subsurface ocean temperature variability in the N3.4 region is associated with ENSO. Hence, the results shown in Fig. 2 imply that ENSO-related SST variability in all considered climate models is relatively high compared with their simulated warm water volume variability, as measured by OHC100 and OHC700, in the N3.4 region. It is unlikely that temporal inhomogeneities in the OHC data are responsible for the disagreement between models, as observation-based results are independent of the considered time period (see Table 2).

We conclude that the underestimation of the strength of the vertical connection between OHC and SST anomalies in the N3.4 region in all considered coupled CMIP runs is a robust finding. The performance of the CMIP3 ensemble is similar to that of the CMIP5 ensemble. Moreover, although the prescribed winds in the CORE2 run lead to realistic simulation of SST variability, the sensitivity of subsurface ocean temperatures is not improved compared to the coupled runs.

This suggests, that the robust underestimation of the ratio of OHC and SST standard deviations in the N3.4 region by the coupled runs cannot be explained solely by the generally too weak Bjerknes Feedback of the climate models (e.g., Bellenger et al. 2014) and may result instead from deficiencies of the ocean models, such as parameterized ocean mixing. The latter is important in coupling SSTs and subsurface ocean temperatures (Boucharel et al. 2015). In the following sections, after examination of the local relationship between SSTs and OHC, we explore the energy budget variability associated with ENSO on a basin scale to investigate whether the underestimation of OHC variability is present in the area-average or spatial error compensation occurs.

3.2 Tropical Pacific energy budget variability

To capture the evolution of the energy budget fields during ENSO events it is useful to explore the relationship with N3.4 at different lags, as done in Trenberth et al. (2002a). Lagged regressions of simulated atmospheric and oceanic energy budget fields area-averaged over the tropical Pacific ocean (30N–30S) onto N3.4 are presented in Fig. 3 (positive lags means N3.4 leads). Analogous diagnostics have been performed by Mayer et al. (2014) using reanalysis data. Here we investigate whether CMIP models are able to reproduce their results, as outlined in Sect. 1.

Fig. 3

Regression of N3.4 onto a Rad_TOA, b F_S (computed from UR Rad_TOA and ERA-I atmospheric budgets, ERA-I Rad_TOA and MERRA budgets, ERA-I Rad_TOA and budgets, respectively), c DIVFA, d OHCT(0–300 m), e OHCT(0–700 m) f DIVFO (full-depth), averaged over tropical Pacific ocean (30S–30N). The shading represents 95 % confidence intervals of the regression coefficients, computed from the residual sum of squares of the respective observational ensemble mean, taking autocorrelation into account

Large differences between models and observation-based estimates (ERA-I, UR) are found for net radiation at TOA (Fig. 3a). The response of Rad_TOA in the Pacific is negative at zero lag in observations; i.e. anomalous energy loss (gain) occurs during El Niño (La Niña), and exhibits a minimum around 4 months lag (−0.10 ± 0.03 PW K⁻¹ in the area integral as estimated from the UR data for the period 1985–2013) which is associated with strong OLR anomalies in the Pacific subtropics (Trenberth et al. 2010). The minimum response as estimated from CERES is in very good agreement with the UR data (−0.12 ± 0.04 PW K⁻¹ at 4 months lag).

Large differences are found among the CMIP5 models. In contrast to observations, most models show positive, and in instances strongly positive, regression coefficients of Rad_TOA (e.g., the CSIRO-Mk6-3-0 maximum response is +0.21 ± 0.06 PW K⁻¹ at −1 month lag). Only the CESM1-CAM5 model shows a Rad_TOA response which is very similar to observations, yet the minimum response occurs a few months later than observed. Considering maps of the differences between modeled and observed response, the largest discrepancies between models and observations are found for the eastern equatorial Pacific regions (not shown). Reasons for this will be discussed in Sect. 3.3, where the breakdown of Rad_TOA into shortwave and longwave components is examined.

The observed net surface flux (F_S) response to ENSO is clearly negative (−0.28 ± 0.07 PW K⁻¹ at 2 months lag for the 1979–2013 period and −0.35 ± 0.11 PW K⁻¹ for the CERES period, see Fig. 3b). Most models agree quite well with the observation-based estimate. The only outliers (CanESM2, MPI-ESM-MR, NorESM1-M, IPSL-CM5A-MR, CSIRO-Mk3-6-0) are the models with the strongest biases in the TOA response (see Fig. 3a). As for Rad_TOA, largest differences between observations and models occur in the eastern equatorial Pacific (see supplements S2). Decomposition of F_S into net radiative surface flux (Rad_S) and turbulent fluxes shows large discrepancies among the modeled Rad_S responses, which resemble the discrepancies among the modeled Rad_TOA responses. The correlation coefficient between Rad_S and Rad_TOA sensitivities from the different datasets is 0.55. Thus, the biased response of Rad_TOA tends to be tightly connected to Rad_S and the underestimation of the F_S response to ENSO in some models. This is in line with Bellenger et al. (2014) who found discrepancies between modeled and observed Rad_S feedback to be larger than between modeled and observed latent heat flux feedback.

Compared to Rad_TOA and F_S, the divergence of lateral atmospheric energy transports (DIVFA) for the tropical Pacific exhibits a regression onto N3.4 that is generally consistent between reanalyses and models (see Fig. 3c). While the ENSO-response of DIVFA in reanalyses is mainly driven by F_S (e.g., Trenberth et al. 2002b; Mayer et al. 2014), the relatively weak response of F_S in models is compensated by the overly strong response of Rad_TOA. Only the two models with the strongest biases in the Rad_TOA response (CanESM2: 0.33 ± 0.02 PW K⁻¹, CSIRO-MK3-6-0: 0.32 ± 0.03 PW K⁻¹, see Fig. 3a) are clearly outside the confidence interval as estimated from atmospheric reanalyses for the period 1979–2013 (0.21 ± 0.04 PW K⁻¹ at one month lag). This confirms the results regarding F_S (Fig. 3b) that errors in Rad_TOA are not reflected in lateral atmospheric transports but rather in the dampening of the net surface flux regression onto N3.4.

Large differences are found for tropical Pacific OHC changes associated with ENSO (see Fig. 3d). In the reanalyses, OHC tendency nearly compensates the atmospheric response (F_S $\approx$ Rad_TOA-DIVFA) to ENSO (OHCT300 response is −0.25 ± 0.06 PW K⁻¹ at zero lag) and consequently the area-averaged DIVFO response is close to zero at lags of a few months or less (F_S $\approx$ OHCT300, see Eq. (2) and Mayer et al. 2014). The observation-based OHCT700 response (−0.29 ± 0.11 PW K⁻¹ at lag −1, Fig. 3e) is slightly stronger compared to OHCT300; i.e. the signal increase between 300 and 700 m is less than 10 % but associated with substantially larger uncertainties. Responses computed for the data-rich period 1992–2013 are −0.27 ± 0.08 PW K⁻¹ and −0.32 ± 0.11 PW K⁻¹ for OHCT300 and OHCT700, respectively, providing extra confidence in the results. These results are consistent with the results of Roemmich and Gilson (2011). We also find positive regression coefficients for tropical Pacific OHCT100 around zero lag, yet these tendencies are overcompensated by the layers below, yielding the negative OHCT300 regression coefficients (not shown).

In contrast to reanalyses, the OHCT signal in models is strongly dependent on integration depth. The regression of OHCT300 against N3.4 (Fig. 3d) is too weak in most models. Only a few coupled models (e.g., GFDL-ESM2M) and the CORE2 run lie within the confidence intervals obtained from reanalyses. Some models additionally exhibit deficiencies in timing; e.g. the HadGEM2-ES model shows almost no OHCT300 response at zero lag and the strongest yet still weak response at more than 1 year lag (−0.14 ± 0.06 PW K⁻¹ at 15 months lag), while ocean reanalyses clearly show a minimum near zero lag. Considering OHCT700 (Fig. 3e), the area-averaged regression coefficient almost vanishes for some models (e.g. NorESM1-M). Most models show a too weak OHCT700 response compared to the best estimate from reanalyses. Only the GFDL-ESM2M (−0.22 ± 0.02 PW K⁻¹), CESM1-CAM5 (−0.21 ± 0.04 PW K⁻¹), and CORE2 (−0.21 ± 0.04 PW K⁻¹) responses at least lie within the uncertainty range of the observation-based estimate. One reason for the generally too weak OHCT response of the models must be a deficient surface flux feedback, but ocean heat transports also play a role (see below). Figure 3d, e also show that the OHCT response from CORE2 outperforms the coupled model runs, demonstrating the benefit from realistic wind forcing and F_S variability. The spatial (horizontal and vertical) structure of the OHCT response is discussed in Sect. 3.4.

Regarding quality of the observations, the divergence of ocean heat transport is the most problematic term considered here. Our observational estimate of the tropical Pacific DIVFO response to ENSO shows a very weakly negative response at small lags and a clearly negative response around 6–8 months lag (−0.11 ± 0.06 PW K⁻¹, see Fig. 3f) which is associated with anomalies in the Indonesian Throughflow transports (see e.g., Mayer et al. 2014 or England and Huang 2005). However, a qualitatively similar result is obtained when computing DIVFO indirectly as residual from F_S and OHCT (see Eq. (2)), which increases the credibility of the results (not shown).

Most models simulate a negative response of the divergence of ocean heat transport to ENSO for 30N to 30S (Fig. 3f), i.e. ocean heat convergence (divergence) anomalies during El Niño (La Niña). This is not surprising when considering the reasonable net surface flux (Fig. 3b) but too weak OHCT (Fig. 3d, e) response to ENSO of most models (see Eq. 2). Moreover, most models show the maximum response of DIVFO around zero lag, i.e. the signal of the lagged response from Indonesian Throughflow transports is non existent in most models. However, some models are in quite good agreement with ORAS4, e.g. GFDL-ESM2M, which also shows the minimum correctly around 6 months lag.

The biased response of modeled tropical Pacific DIVFO (Fig. 3f) may be related to the generally too narrow band of ENSO-related wind stress anomalies along the equator in the coupled climate models (Capotondi et al. 2006). Along the equator, DIVFO variability is mainly associated with Sverdrup transports resulting from equatorial wind stress curl anomalies (Jin 1997; Clarke et al. 2007) and compensating DIVFO anomalies of opposite sign occur in the subtropics. Indeed, all considered datasets (reanalyses and models) have a positive response of equatorial (5N–5S) DIVFO to ENSO with all models exhibiting a weaker response than reanalyses (not shown). A positive equatorial DIVFO response in combination with a negative DIVFO response in the tropical Pacific (30N–30S) area average (Fig. 3f) requires an area symmetrical about the equator where models simulate a balance between F_S and OHCT, i.e. vanishing DIVFO (see Eq. 2). This occurs around 20N–20S in all models, while ORAS4 exhibits strong positive regression coefficients at these latitudes (see supplements S3). This indicates that the variability of DIVFO associated with equatorial wind stress curl anomalies indeed is simulated in a too narrow band about the equator and thus affects an area too narrow about the equator.

We performed analogous diagnostics for Rad_TOA, F_S, OHCT300, and OHCT700 for the CMIP3 model ensemble (see supplements S4). The results were remarkably similar to those obtained from the CMIP5 models, i.e. similarly biased responses of Rad_TOA and OHCT are apparent.

3.3 Radiation at TOA in the tropical Pacific

The spatial structure of Rad_TOA regression coefficients reveals that the largest differences between observations and models are present in the equatorial Pacific, east of the dateline (not shown). This is the region of the well-known cold tongue bias of the models but also the region of largest SST variability associated with ENSO. To explore these differences further we consider the response of OLR, ASR, and Rad_TOA in the eastern equatorial Pacific (10S–10N, 155W–70W) to N3.4 anomalies. The differences across models are large generally and thus scatter plots of OLR, ASR and Rad_TOA versus N3.4 are presented in Fig. 4 for two models representing the range of model behavior along with our composited observational estimate (see description in Sect. 2). December values are highlighted in red as SST anomalies typically peak at that time (Trenberth 1997) and they most clearly depict the features described below.

Fig. 4

Scatter plot of N3.4 versus a OLR, b ASR, and c Rad_TOA (net) in the eastern equatorial Pacific Ocean (10S–10N, 155W–90W) from observations; d, e, f as (a), (b), (c), but for IPSL-CM5A-MR; g, h, i as (a), (b), (c), but for GFDL-ESM2M; Black crosses represent all monthly anomalies and red squares represent all December anomalies

The response to N3.4 of OLR, ASR and Rad_TOA from observations (Fig. 4a, b, c) is as expected for the Pacific Intertropical-Convergence Zone (ITCZ) region, where variability of high convective clouds plays a dominant role in modifying radiation (Trenberth et al. 2015). Both OLR and ASR decrease with increasing SST anomalies, closely compensating each other and thus the response of Rad_TOA to SST variability is very small (note that Rad_TOA = ASR–OLR), which is in line with the findings of Kiehl (1994). Non-linearities are present for strong El Niño events and are associated with deep convection (see also Lloyd et al. 2012). These non-linearities are probably related both to the point when anomalous deep convection east of 155W sets in and the eastward extension of SST anomalies, which depends on the strength of the respective ENSO event.

The IPSL-CM5A-MR model exhibits a quite linear negative response of OLR (Fig. 4d) and, in disagreement with observations, a linear positive ASR response (Fig. 4e) to N3.4. As a result, Rad_TOA (Fig. 4f) exhibits a linear (positive) regression against N3.4 (+5.1 W m⁻² K⁻¹).

Similar to observations and quite contrary to the IPSL model, OLR from the GFDL-ESM2M model (Fig. 4g) shows little change for negative and moderately positive SST anomalies, but a strong negative response is present for SST anomalies exceeding about 1.5 K. The response of ASR to SST anomalies in the GFDL-ESM2M model (Fig. 4h) is moderately positive for anomalies lower than about 1.5 K, but strongly negative for SST anomalies larger than this threshold value. It should be noted that the strong ASR and OLR non-linearities in GFDL-ESM2M occur for very strong SST anomalies, but are not observed. Despite these strong non-linearities, Rad_TOA (Fig. 4i) exhibits a comparatively weak non-linear relationship to N3.4 and a positive response to ENSO (+2.4 W m⁻² K⁻¹). When performing separate regression analyses for positive and negative anomalies, the coefficients for Rad_TOA are 3.3 and 1.6 W m⁻² K⁻¹, respectively.

One reason for the large differences in model behavior may be associated with the model mean state. For investigation of the shortwave feedback at the surface, Bellenger et al. (2014) distinguished between models with three different regimes of atmospheric stability including subsident, convective and a mixed regime, which switches between subsident and convective during ENSO. Here we adopt this distinction for our exploration of TOA fluxes, and we employ precipitation response in the eastern Pacific ITCZ region (10S–10N, 155W–70W) to ENSO as a simple indicator of the regime in the considered models. Weak response of precipitation to SST anomalies indicates persistent subsidence conditions in a model such that even strong positive SST anomalies cannot trigger convection. A strong response of precipitation to ENSO indicates either a mixed type regime or convective regime. In a subsidence regime, OLR responds slightly negatively to El Niño due to changes in cloud top temperatures, but ASR responds positively, as low-level cloud cover decreases in the eastern equatorial Pacific stratocumulus regions. In a mixed regime, OLR is strongly reduced when switching from subsident to convective conditions because of cold cloud tops, while ASR decreases from the greater cloud cover with increasing SSTs.

A scatter plot of OLR versus precipitation regressions against N3.4 (Fig. 5a) indeed shows a clear relationship between OLR and precipitation sensitivities to ENSO across models. Models with low precipitation sensitivity exhibit low OLR sensitivity and vice versa. The analogous plot showing ASR versus precipitation regressions against N3.4 (Fig. 5b) clearly shows the change of sign of the ASR regression coefficients depending on the climatological regime of the respective model. To account for the strong non-linearities in the ASR and OLR responses, Fig. 5a, b represent linear regressions for positive N3.4 anomalies.

Fig. 5

Scatter plot of a OLR and b ASR regressed onto N3.4 on the y-axis and precipitation regressed onto N3.4 averaged over the eastern equatorial Pacific Ocean (10S–10N, 155W–90W). Only ASR and OLR anomalies associated with positive N3.4 anomalies are considered for the regression to account for the strong non-linearities

As in models with strong subsidence in the eastern equatorial Pacific OLR is negatively and ASR is positively correlated with N3.4, they exhibit a positive Rad_TOA signal associated with N3.4 which is in line with the findings of Clement et al. (2009). Mixed-type and convective-type models exhibit almost compensating ASR and OLR anomalies for negative and moderately positive N3.4 anomalies, but for strong positive N3.4 anomalies the stronger OLR non-linearity outweighs ASR anomalies (see Fig. 4g–h), yielding a non-linear increase in Rad_TOA (Fig. 4i). Similar results are found for other mixed-type models (not shown), though it is important to note that these non-linearities arise for strong positive SST anomalies that exceed those observed. It is important to note that besides the model mean state, the frequency of extreme El Niño events also contributes to the non-linearity of the radiative flux responses, as noted by Lloyd et al. (2012). Indeed, the correlation coefficient between ASR non-linearity and the frequency of extreme El Niños (N3.4 > 2σ of the observed N3.4 index) is −0.66 (see supplements S5).

Thus, the generally excessive positive regression coefficients for Rad_TOA found in models may be due to biased mean conditions in case of subsidence models and, at least partly, to the unrealistically large SST variance exhibited by mixed-type models.

3.4 Spatial structure of OHC changes in the tropical Pacific

The modeled regression of tropical Pacific OHCT300 onto N3.4 (Fig. 3d) is in better agreement with reanalyses than that of OHCT700 (Fig. 3e). This implies that that the area-integrated OHCT response of the 300–700 m layer in the considered CMIP5 models tends to damp the signal of the upper 300 m, especially at small lags. To explore this further we consider the spatial structure of OHCT regressions onto N3.4 in different layers from ORAS4, GFDL-ESM2M, and IPSL-CM5A-MR at zero lag.

Regressed OHCT300 fields (Fig. 6a, c, e) show the eastward displacement of warm water from the western tropical Pacific during El Niño. The structures from reanalysis and models are quite similar, but the magnitude of the regression coefficients is generally higher in ORAS4 compared to GFDL-ESM2M and IPSL-CM5A-MR (RMS value over tropical Pacific is 17.7, 15.0 and 12.0 W m⁻² K⁻¹, respectively). The area integrals of tropical Pacific OHCT300 regression coefficients from GFDL-ESM2M agree with ORAS4 within uncertainty bounds but the area averaged signal from IPSL-CM5A-MR is clearly too low (see Fig. 3d).

Fig. 6

a OHCT300 and b OHCT700-OHCT300 regressed onto N3.4 at zero lag from ORAS4; Figures c–d same as a–b but for GFDL-ESM2M; Figures e–f same as a–b but for IPSL-CM5A-MR

The structure of regressed OHCT between 300 and 700 m (OHCT700-300, Fig. 6b, d, f) is different from that for the upper 300 m. There exist two large regions with negative regression coefficients including the eastern equatorial Pacific and the region east of Australia and south of the equator, referred to here as the South Pacific Convergence Zone (SPCZ) region (approximately 15S–5S, 150E–155W). The SPCZ region exhibits a strong negative response of surface wind stress curl to ENSO, the strongest in the whole tropical Pacific (Clarke et al. 2007). Regressed OHCT fields in the SPCZ region show a uniformly negative sign in the upper 700 m (Fig. 6a–f). This is associated with upwelling (downwelling) water due to Ekman transports during El Niño (La Niña). Surface flux contributions to OHCT in that region are negligible (not shown), but lateral divergences could also play a role. The regressed fields from models are in relatively good qualitative agreement with ORAS4, but the magnitude of the coefficients is lower (RMS value over tropical Pacific is 7.3, 5.1, and 4.4 W m⁻² K⁻¹ for ORAS4, GFDL-ESM2M, and IPSL-CM5A-MR respectively). Thus, the regressed OHCT fields from models and reanalyses agree quite well structurally (Fig. 6a–f) but their area-averages disagree (Fig. 3d–e). This suggests that similar mechanisms modifying OHC are at work in the models, but their modeled strength is biased.

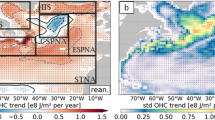
Figure 7a, b show regression coefficients of OHCT300 onto N3.4 and OHCT700-300 onto N3.4, respectively, averaged over the SPCZ region for all employed ocean datasets at different lags. The observation-based datasets clearly show the strongest response to ENSO (approximately −50 W m⁻² K⁻¹ or −0.4 PW K⁻¹ for the full 0–700 m layer). The coupled models show a weaker response, but the CORE2 run is in quite good agreement with the reanalyses even in the 300–700 m layer and outperforms its coupled counterpart CCSM4. This suggests that realistic wind stress (curl) and associated Ekman pumping is essential in obtaining the observed OHCT signal in the SPCZ region.

Fig. 7

Regression of a OHCT300 and b OHCT(700–300) onto N3.4 averaged over the SPCZ region (15S–5S, 150E–155W)

To quantify this relationship, we compute Ekman velocity w _e following Lysne and Deser (2002) at the lower boundary of the Ekman layer according to $w_{e} = \frac{\text{curl}\left( \tau \right)}{\rho f}$ (positive upward), where $\rho$ is sea water density (set to 1026 kg m^− 3), $\tau$ the surface wind stress, and f the Coriolis parameter. Considering anomalies and neglecting horizontal advection, the local rate of change of temperature anomaly is governed by vertical advection of the time-mean vertical temperature gradient by $w_{e}$ anomalies and is given by $\frac{{dT^{'} }}{dt} = w_{e}^{'} \frac{d\overline{T}}{dz}$. Ekman velocity varies with depth, but its sign is uniform across the column, and $\bar{T}$ generally decreases with depth. Thus, rising motion will cool the column, and sinking motion will warm the column, and hence OHCT is proportional to w _e .

Figure 8a clearly shows the strong relation between OHCT700 and w _e , i.e. a strong response of w _e to ENSO in the SPCZ region is associated with a strong response of OHCT700 to ENSO in the same region, and vice versa. The generally too weak simulated wind stress curl (and thus w _e ) response to ENSO in the SPCZ region is associated with the generally too weak Bjerknes feedback (following Bellenger et al. 2014 defined as the regression of the zonal wind stress in the Niño 4 region onto Niño 3 SST anomalies) in the models, as can be seen from Fig. 8b. Note that here N3 is chosen as an ENSO index in order to be consistent with the computation of the Bjerknes feedback. There is no very strong linear relationship across models, but as all models exhibit a Bjerknes feedback that is too weak, they also exhibit a deficient wind stress curl response.

Fig. 8

a X-axis: Regression of w _e onto N3.4, y-axis: regression of OHCT700 onto N3.4 (SPCZ area averages); b X-axis: Regression of w _e (SPCZ area average) onto N3, y-axis: Bjerknes feedback (defined as regression of $\tau_{x}$ in N4 region onto SST in N3 region); c X-axis: regression of monthly thermocline depth tendency onto w _e , y-axis: regression of OHCT700 onto w _e (SPCZ area averages); d X-axis: regression of OHCT700 onto monthly thermocline depth tendency (SPCZ area average), y-axis: residuals from the regression line in Fig. 8c. Observation-based Bjerknes feedback and w _e are computed from ERA-I data

The underestimated response of the wind stress curl to ENSO in the models is only one reason for the weak OHCT signal in the SPCZ region. In Fig. 8c we present a scatter plot with regression coefficients of OHCT700 onto local w _e on the y-axis and regression coefficients of monthly thermocline depth changes onto local w _e on the x-axis. There is a very clear linear relationship between OHCT sensitivities to w _e and the sensitivity of thermocline depth to w _e , and the range of regression coefficients is large, with ORAS4 being among the models with the highest sensitivities. Some models exhibit less than half of the sensitivity to wind stress curl. The strong relationship between the respective response of thermocline displacement and OHCT to w _e is not surprising, as the vertical temperature gradient is strongest at the thermocline, and hence its vertical displacement will effectively alter OHC in the column.

However, it is difficult to explain the still relatively large range of values of sensitivities as seen from Fig. 8c. We find the mean thermocline depth to play a minor role (not shown). Possible explanations are differences in horizontal advection and associated heat divergence as a response to w _e but also uncertainties in tunable ocean parameterizations probably play a role.

As OHCT700 and thermocline depth tendency are very highly correlated (r > 0.95 in all considered datasets), the residuals from the regression line in Fig. 8c can be explained very well by differences of sensitivities of OHC700 to thermocline depth tendency in the different datasets (see scatter plot in Fig. 8d), which must be due to differences in the time mean vertical temperature gradient, i.e. thermocline sharpness, in the different datasets, which is obviously too low in all considered models.

The large discrepancies between models and observations found for the OHCT700-300 response to N3.4 in the eastern equatorial Pacific (see Fig. 6b, d, f) are not explored in detail as the uncertainty among the observational estimates is comparatively large in that region. However, a preliminary examination of the linearized temperature advection equation indicates that below 300 m anomalous vertical advection of the mean vertical temperature gradient plays a dominant role. Models with a weak mean vertical temperature gradient tend to lack a strong OHCT signal below 300 m.

3.5 Teleconnections to tropical Atlantic

Pacific ENSO signals are communicated to the Atlantic via alteration of the tropical Walker and Hadley Cells, the so-called atmospheric bridge (Klein et al. 1999). These changes in the large-scale circulation act to alter both tropical Atlantic Rad_S and turbulent fluxes in various ways. North Atlantic trade winds are weakened (enhanced) during El Niño (La Niña) leading to reduced (enhanced) evaporation. Moreover, increased (decreased) tropospheric temperatures stabilize (destabilize) the atmosphere and consequently precipitation along the Atlantic ITCZ and in the Amazonas basin decreases (increases) during warm (cold) ENSO events. In convective regions over the ocean the so-called “tropospheric temperature mechanism” (see Chiang and Sobel 2002 and Chiang and Lintner 2005) leads to (1) reduced (enhanced) evaporation mainly associated with boundary layer humidity changes and (2) increased (reduced) net surface radiation associated with changes in clouds during El Niño (La Niña). Consistent with changes in F_S, atmospheric energy export from the tropical Atlantic decreases (increases) and tropical Atlantic OHC increases (decreases) during El Niño (La Niña). During peak ENSO, the area-integrated tropical Atlantic OHCT300 signal (units of PW K⁻¹) as estimated from reanalyses compensates for about 45 % of the tropical Pacific signal and is even stronger than that found for the tropical Pacific in an area-specific sense (units of Wm⁻² K⁻¹; Mayer et al. 2014). In this section we investigate whether CMIP models exhibit a similar behavior.

Regressions of area averages over the tropical Atlantic (30N–30S) of DIVFA, F_S, and OHCT300 onto N3.4 are presented in Fig. 9a, b, c, as a function of lag. All models qualitatively resemble the behavior found from reanalyses: total energy export from the tropical Atlantic region is reduced (enhanced) during El Niño (La Niña), mainly due to anomalous surface fluxes into (out of) the ocean. Therefore, OHC increases (decreases) during El Niño (La Niña) events. However, the response of the Atlantic energy budget to ENSO is generally weaker in the models compared to reanalyses. For example, the magnitude of the peak response of DIVFA to N3.4 in the GISS-E2-R model (−0.07 ± 0.01 PW K⁻¹) is 50 % low compared to ERA-I and MERRA (−0.14 ± 0.03 PW K⁻¹; Fig. 9a). The differences in F_S are even more obvious and the models show robust biases in underestimating the influence of ENSO (0.06–0.09 PW K⁻¹ in models versus 0.13 ± 0.03 PW K⁻¹ in reanalyses; Fig. 9b); an underestimate also seen in surface turbulent fluxes and radiative fluxes (discussed below) in most models. Consequently, the regression coefficients of OHCT300 between lags 6 and −6 months are comparatively low in all models (0.08–0.10 PW K⁻¹) but within uncertainty bounds of the observational estimate (+0.12 ± 0.05 PW K⁻¹; Fig. 9c). The differences between OHCT300 and F_S responses arise from comparatively small yet non-zero responses of tropical Atlantic DIVFO. We also note that observation-based results for the 1992–2013 period are very similar compared to those shown in Fig. 9.

Fig. 9

Regression of a DIVFA, b F_S, c OHCT(0–300 m) onto N3.4, averaged over the tropical Atlantic ocean (30S–30N). The shading represents 95 % confidence intervals of the regression coefficients, computed from the residual sum of squares of the respective observational ensemble mean, taking autocorrelation into account

We first examine the strength of teleconnections to the Atlantic as measured by changes of north Atlantic trade wind strength. It is underestimated by most of the considered models (see supplements S6). This is probably related to the fact that a too large fraction of ENSO events in CMIP models peak in the central Pacific when compared to observations (Bellenger et al. 2014), and Taschetto et al. (2015) have shown that ENSO events peaking in the central Pacific exhibit significantly weaker teleconnections to the Atlantic compared to those peaking in the eastern Pacific. However, the relation between turbulent flux response to N3.4 and 10 m wind speed response to N3.4 in the northern Atlantic trade wind region is not very strong (see Fig. 10a). While results from a large fraction of data sets scale quite linearly (weak wind response associated with weak turbulent flux response and vice versa), some models do not follow this expected pattern.

Fig. 10

a x-axis: 10 m wind speed in the north Atlantic trade wind region (10N–25N, 65W–10W) regressed onto N3.4, y-axis: turbulent fluxes in the north Atlantic trade wind region (10N–25N, 65W–10W) regressed onto N3.4; b x-axis: precipitation in the western Atlantic ITCZ region (10S–10N, west of 10W) regressed onto N3.4, y-axis: F_S in the western Atlantic ITCZ region (10S–10N, west of 10W) regressed onto N3.4; c x-axis: Turbulent surface flux regressed onto N3.4, y-axis: Rad_S regressed onto N3.4 (area-averaged over tropical Atlantic)

The three models with the strongest (yet still too weak) turbulent flux response to ENSO in the north Atlantic trades region (ACCESS1-0, ACCESS1-3, HadGEM2-ES) exhibit an extremely low wind speed response to ENSO. This fact might be related to the comparatively low mean near-surface relative humidity simulated by these models in this region (not shown) enhancing the sensitivity to wind speed variations and the comparatively strong negative surface radiation response to ENSO of these models (not shown) which is associated with cloud and precipitation changes in the Caribbean and east of it (Enfield 1996). The negative Rad_S response damps the positive SST response to ENSO and in this way can amplify the positive turbulent flux response (Foltz and McPhaden 2006).

As a second indicator of teleconnection strength we assess the “tropospheric temperature mechanism”. Following Chiang and Lintner (2005) we expect its largest impact on surface fluxes along the Atlantic ITCZ. However, although tropical Atlantic tropospheric temperatures in the models are similarly or even more sensitive to ENSO compared to observations (see supplements S7), the Atlantic ITCZ still exhibits an underestimation of the F_S response by the models (see supplements S2). Figure 10b reveals that the underestimated F_S response of the models in the Atlantic ITCZ is related to a too weak precipitation response in that region (r = −0.75). The deficient precipitation and related cloud response of the models is likely linked to the model mean convective activity in that region which is known to be biased low in association with local biases, such as too cold SSTs (Richter et al. 2014).

Considering the full tropical Atlantic, a scatter plot of Rad_S sensitivity versus turbulent flux sensitivity (Fig. 10c) shows that generally models with a strong response of turbulent fluxes to ENSO tend to have low Rad_S sensitivity and vice versa. This highlights that considerable differences exist regarding the contributions to the F_S response from the various processes described above, but F_S regression coefficients in the tropical Atlantic as a measure of overall teleconnection strength at zero lag are uniformly low in the models (see Fig. 9b).

For brevity, and as observation-based results are comparatively uncertain in the Indian Ocean (Mayer et al. 2014), we do not show a separate assessment of that basin but proceed with the zonal mean results.

3.6 Tropical zonal mean response

The zonally averaged response of net radiation at TOA (Fig. 11a) qualitatively resembles the results for the tropical Pacific (Fig. 3a), indicating that the Rad_TOA response to ENSO in the tropical Pacific dominates the zonal mean. The peak response from observations is −0.10 ± 0.03 PW K⁻¹ at 4 months lag (−0.12 ± 0.04 PW K⁻¹ for the CERES period). The biased Pacific response shown by most models (Sect. 3.3) is most notable at small lags (Fig. 11a). A large fraction of the models show negative regression coefficients only at excessive positive lags.

Fig. 11

Regression of a Rad_TOA, b DIVFA, and c OHCT300 onto N3.4 averaged over all three tropical (30N–30S) ocean basins

The zonal mean atmospheric energy export response to ENSO (Fig. 11b) is relatively small owing to compensating responses of the tropical Pacific and the other tropical basins. As described by Mayer et al. (2014), the DIVFA response is small at zero lag, when this compensation is strongest, and it peaks at 8 months lag (0.10 ± 0.06 PW K⁻¹), when the strength of the teleconnections ceases. The zonally averaged response of DIVFA to ENSO of many models compares favorably with results from reanalyses, with a few tending to underestimate the response (CESM1-CAM5, CCSM4, NorESM1-M).

The zonal mean OHCT300 response is relatively weak at small lags as the strong energy dis-/recharge signal in the tropical Pacific (see Fig. 3d) is largely compensated by OHCT300 responses of the opposite sign in the other basins. However, ocean reanalyses show moderately negative OHCT300 regression coefficients for lags between −12 and +22 months, with the strongest response around 1 year lag (−012 ± 0.08 PW K⁻¹, see Fig. 11c). Results of the regression analysis for the 1992–2013 period are very similar, but uncertainties for the zonally averaged OHCT700 response are large and therefore not discussed here. All models show ocean heat loss (gain) during El Niño (La Niña) events at least at some lags (Fig. 11c). However, similar to the results for the Pacific basin, the biased response of Rad_TOA (see Sect. 3.3) has a clear imprint on the zonally averaged OHCT300 to ENSO, leading to a (partly strong) positive OHCT300 response around zero lag. Averaging the months with a negative observed OHCT300 response (lag −12 to +22 months), the observational estimate over these 35 months is about −0.06 PW K⁻¹. Only the MIROC5 and GFDL-ESM2M models exhibit a similar time-averaged response (−0.08 PW K⁻¹ and −0.05 PW K⁻¹, respectively), while all other models show a too weak response, some of which even show a positive response over this period (e.g., IPSL-CM5A-MR). Hence, the zonal mean OHC300 variability associated with ENSO is underestimated in all models except for two.

4 Conclusions

The variability of the coupled atmosphere–ocean energy budget in association with ENSO bas been evaluated from observational datasets and CMIP models. Investigation of the response of the tropical Pacific energy budget to ENSO reveals serious model deficiencies. Most of the models considered underestimate and some completely lack an area-averaged ENSO signal in 0–700 m OHCT, while reanalyses clearly show pronounced basin-wide OHC discharge (recharge) associated with El Niño (La Niña) (see Sect. 3.2). Various shortcomings of the models contribute to the underestimation of this basic feature of ENSO.

First, most models exhibit a biased response of Rad_TOA to ENSO which projects on surface fluxes and consequently also on OHCT. This is related to biased mean convective activity in the eastern Pacific ITCZ region in many models, with some incorrectly staying in a subsidence regime independent of ENSO state (Bellenger et al. 2014). Radiation is then mainly modulated through changes in low level cloud amount, leading to a positive response of TOA net radiation to ENSO in this region, as opposed to the expected neutral response of Rad_TOA to SST anomalies (Kiehl 1994). Models with unrealistically high SST variance correctly switch between subsident and convective states in association with ENSO. However, these models also suffer from problems with low clouds and simulate an ASR response of the wrong (positive) sign for moderate SST anomalies. In combination with excessively strong non-linearities in the OLR response associated with convective cloud tops, the Rad_TOA response to ENSO in the eastern Pacific ITCZ region is positive also for this type of models (see Sect. 3.3).

Second, the well-known underestimation of the Bjerknes Feedback and more generally the biased response of wind stress curl patterns to ENSO lead to a biased local redistribution of OHC during ENSO events. All models exhibit at least reasonable spatial structure in the OHCT response to ENSO, but it is generally deficient in magnitude compared to reanalyses. For example, strong ocean cooling (warming) in the SPCZ region associated with Ekman pumping during warm (cold) ENSO events as found from reanalyses is underestimated by the models, contributing to the basin-wide underestimation of the modeled OHCT response to ENSO (see Sect. 3.4).

Third, too weak of a vertical connection between OHC and SST anomalies in the N3.4 region as measured by the ratio of their respective temporal standard deviations is a feature common to all models considered. The generally deficient Bjerknes Feedback in the models is unlikely to be the sole reason for this deficiency as this behavior is also present in an ocean model run forced by observed winds (CORE2). This suggests that model physics are not tuned ideally, at least for the considered region (see Sect. 3.1).

Teleconnections to the tropical Atlantic are found to be represented too weakly in all considered models. Especially the positive response of net surface energy flux to ENSO is uniformly underestimated by about 50 %, which projects also on the OHC response in the tropical Atlantic. We identify two model shortcomings that contribute to this biased response including (1) a too weak trade wind response to ENSO that is likely associated with errors in the location of Pacific SST anomalies (Taschetto et al. 2015) and (2) the failure of the tropospheric temperature mechanism which likely relates to deficient mean Atlantic ITCZ precipitation.

The response of tropical zonal mean TOA net radiation is lagged compared to observations, including unrealistic net energy input to the system during the peak of El Niño events. This biased behavior can be attributed to cloud and precipitation biases in the eastern Pacific ITCZ region as discussed above. The biased TOA response projects on net surface energy flux and thus OHC in the Pacific but the dynamical coupling between atmosphere and ocean also plays a role. Although the OHC response to ENSO in the tropical Atlantic which tends to partly compensate the area-averaged Pacific OHC signal (Mayer et al. 2014) is clearly underestimated by the models, the tropical zonal mean OHC variability associated with ENSO is far too weak in all but two models. A ranking of model performance based on the distance between observations and models as found from central diagnostics of this study (Figs. 2c, 3e, 5, 9c, 11c) reveals that of the coupled CMIP5 models GFDL-ESM2M, MIROC5, and CESM1-CAM5 perform best. The CORE2 run outperforms all considered coupled models, although it also exhibits shortcomings like the too weak link between SST and OHC in the N3.4 region (Fig. 2a–d).

This study shows that key aspects of ENSO, namely (1) net radiative energy loss (gain) at TOA, (2) ocean heat discharge (recharge) in the tropical Pacific and (3) compensating OHC tendencies of the opposite sign in the tropical Atlantic and Indian Oceans during warm (cold) events, are underestimated in all considered models and partly missing in some models. Moreover and in accordance with (Flato et al. 2013), our results also show that the main improvement of CMIP5 models over preceding CMIP3 models regarding the energetic aspects of ENSO explored in the present study is the reduced number of outliers.

The biases identified here in coupled models have implications for efforts to infer climate sensitivity from the observational record (e.g., Dessler 2010; Trenberth et al. 2015). The goal of these works is to infer feedbacks of key processes (i.e. clouds) that are fundamental to long-term changes. A related challenge is that the observed magnitudes of changes in surface temperature are governed not only by the magnitude of these feedbacks but also by potentially unrelated factors, such as properties of the mean state (e.g. ocean mixed layer depth) and other processes (e.g. mixing strength). Here we show that many of these additional factors are likely biased in models and hence may preclude a direct assessment of the feedbacks that govern sensitivity.

Appendix 1 List of acronyms

Table 3