Abstract
A multi-scale moisture budget analysis is used to identify the mechanisms responsible for the sensitivity of the water cycle to spatial resolution using idealized regional aquaplanet simulations. In the higher resolution simulations, moisture transport by eddy fluxes dry the boundary layer enhancing evaporation and precipitation. This effect of eddies, which is underestimated by the physics parameterizations in the low-resolution simulations, is found to be responsible for the sensitivity of the water cycle both directly, and through its upscale effects on the transport of mean moisture by the mean circulation. Correlations among moisture transport by eddies at adjacent ranges of scales provides a potential for reducing this sensitivity by representing the unresolved eddies by their marginally resolved counterparts.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Regional models have been extensively used for weather forecast and climate process studies for decades because they can resolve mesoscale atmospheric processes and more detailed topography and land-use characteristics at lower computational cost than conventional GCMs. Evidence of improvements in simulating the magnitude and frequency distribution of precipitation with increased spatial resolution, especially over regions with strong orography or land-use contrast, is widely documented (Giorgi and Marinucci 1996; Leung and Qian 2003; Gent et al. 2009). However, the overall value of using regional models with high spatial resolution to downscale climate information is still not clear. This is partly because their internal physics does not necessarily allow them to produce large-scale circulation consistent with the forcing imposed on the lateral boundaries (Castro et al. 2005). Even if a regional high-resolution model uses the same physics package as the forcing GCM, inconsistency in the large-scale circulation may still occur if the physics package is sensitive to spatial resolution, thus compromising the value of the regional model as a tool for downscaling. The issue of physics dependence on spatial resolution is an important area of research not only because of its implications for nested regional modeling, but also for variable and high resolution global modeling, which is becoming increasingly viable for climate modeling at the regional scale.
A survey of recent studies on model sensitivity to spatial resolution suggests that whether increased resolution improves or degrades a simulation appears to depend on the model as well as the specific processes being examined. Using the Japanese Meteorological Agency global spectral model (JMA-GSM) run at 20 km grid-spacing, Mizuta et al. (2006) showed that the model captures the global distribution of precipitation and surface pressure well but it over estimates the magnitude of precipitation as well as upper tropospheric temperature compared to observations. In the ECMWF model (Jung et al. 2012), on the other hand, improvement in tropical precipitation and tropical atmospheric circulation is found with successive increase of spatial resolution from T159 (126 km), T511 (39 km), T1279 (16 km), to T2047 (10 km), with most improvement found between resolution of 126 and 39 km. In a similar study using Geophysical Fluid Dynamics Laboratory (GFDL) AM2 run at 2°, 1°, 0.5°, and 0.25°, Lau and Ploshay (2009) showed that higher-resolution models captured the precipitation modulation produced by topographical forcing, but errors in precipitation that were already in the coarser grid simulations were enhanced. In a recent study on the impact of resolution of climate model forecasts of precipitation during tropical warm pool-international cloud experiment (TWP-ICE) using the community atmospheric model (version 4), Boyle and Klein (2010) showed that the model biases in mean precipitation are not improved by resolution. In fact, they find that the finest resolution simulation (0.25° grid-spacing) overestimates precipitation as well as diabatic heating by the largest amount.
While there is a long list of studies that document the sensitivity of precipitation to model spatial resolution, studies that aim to understand the mechanisms of the sensitivities and/or propose methods to eliminate or reduce them are just beginning to appear (Arakawa et al. 2011 is one example). Traditionally cumulus parameterizations aim to represent the eddy transport of temperature and moisture (and sometimes momentum) as well as their sub-grid scale sources and sinks. They are generally designed for grid spacing of the order of hundreds of kilometers where statistical balance between convection and the large-scale environment, often called “convective quasi-equilibrium” (Arakawa and Schubert 1974) is assumed. If there is no external fine-scale information introduced to the system through topography, land use variability, etc., the resolved fields obtained from a low resolution model simulation that uses a cumulus parameterization should be consistent with those obtained from a cloud resolving simulation with the same dynamical model when spatially averaged to the low resolution of the former. From a model physics point of view, this means the parameterized sources of heat and moisture in the low resolution model must match the required parameterized source (RPS, after Jung and Arakawa 2004) obtained from the same model run at cloud resolving scale (i.e., without convective parameterizations). Jung and Arakawa (2004) used a two-dimensional cloud system resolving model (CSRM) and a large-scale dynamical model, which is a coarser resolution version of CSRM, to investigate the sensitivity of the RPS to model resolution. They found that the RPS is highly dependent on horizontal resolution in the range of typical resolutions of mesoscale models as well as the model physics time step. Therefore they note that model physics in future prediction models should produce the resolution dependencies so that the need for retuning parameterizations as resolution changes can be minimized.
As discussed in the above studies, alleviating model sensitivity to spatial resolution by allowing the parameterized sources to evolve through the range of spatial resolutions in a way that matches the required parameterized sources derived from higher resolution simulations is imperative to yield optimal model skill at a wide range of scales. As a step toward this end, this study applies a multi-scale moisture budget analysis on idealized regional model simulations to:
-
1.
identify the causes of model sensitivity of the water cycle to spatial resolution,
-
2.
quantify the errors in the eddy fluxes from cumulus parameterizations at various scales and,
-
3.
explore the relationships among eddy fluxes at adjacent scales for potential parameterization applications.
2 Model description and experiment set-up
The model used in this study is the advanced research weather research and forecasting (WRF V3.2, Skamarock et al. 2008) model coupled with the community atmospheric model version 4 (CAM4, Collins et al. 2004) physics package. As part of a project to compare the effects of dynamical frameworks and model resolution on climate simulations using three different dycores of CAM and WRF, the CAM4 physics package was chosen to maintain consistency across the models (Hagos et al. 2013). The CAM4 physics schemes for deep convection (Zhang and McFarlane 1995 after modifications by Neale et al. 2008; Richter and Rasch 2008), stratiform cloud (Rasch and Kristj’ansson 1998), boundary layer turbulence (Holtslag and Boville 1993), and radiation (Collins et al. 2004) were ported to WRF with an attempt to change them as little as possible from how they are used in CAM4. However, it should be noted that some differences are inevitable due to differences in model infrastructure, and some of the differences could lead to subtle changes in the behavior of the schemes in WRF versus in CAM4. The most important difference is the order in which the physics schemes are called. In CAM4, each scheme is called sequentially, with the model state updated at the end of each scheme before the next is called. So, each scheme sees a different model state. By comparison, WRF calls each physics scheme using the same model state, accumulates the tendencies from all the schemes during a given time step, and then applies the tendency after all the schemes have been called. The one exception is microphysics, which is called at the end of the time step after tendencies from advection and the other schemes have been applied.
Another potentially significant difference between CAM4 and WRF is the time step. In CAM4, the typical time step is 30 min, which is used for both advection and physics. In WRF, the higher resolutions require shorter time steps. In this study the physics schemes are called every 10 min while the dynamics time step is 2 min. Cloud fraction is calculated in the radiation scheme using the methodology from Randall (1996). Also, the bulk aerosol treatment used in CAM4 is not used in the WRF simulations.
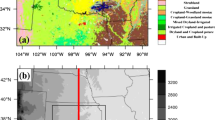
To assess the sensitivity to model resolution over a wide range of scales, this study uses two nested aquaplanet experiments with zonally uniform and time invariant SST. In a typical regional climate simulation, the lateral boundary conditions for the regional simulation are derived from a global climate simulation. In this configuration, the regional simulation may differ from the global simulation not only because of grid resolution, but also because of differences in the numerical solvers and possibly physics parameterizations. Since our goal is to assess the effects of model resolution on moisture transport by eddy fluxes, we choose to use nested configurations of WRF to compare the high-resolution and low-resolution simulations in the same modeling framework. Because wave propagations are prominent in the tropics, we select a large tropical channel domain for the coarse resolution to minimize the impacts of lateral boundary treatments (e.g., Ray et al. 2011). In the first experiment, a high-resolution regional domain with 0.2° grid spacing (hereafter HRM) is nested in a tropical channel domain with 1.0° grid spacing (TCM). In the second experiment, a cloud resolving regional domain with 0.04° grid spacing (CRM) is nested in a high-resolution tropical channel model with 0.2° grid spacing (HRTCM). The experiment set-up is depicted in Fig. 1. The two sets of simulations facilitate analysis of simulations spanning the range from 0.04°, 0.2°, to 1° grid spacing. The lateral boundary conditions for the tropical channel experiments and the sea surface temperature data for all the experiments are obtained from a CAM4 aquaplanet simulation where the SST is zonally uniform and constant in time using the meridional structure shown in Fig. 1b. Because of the zonal symmetry and the large tropical channel domain, the impacts of CAM4 boundary conditions on the WRF simulations should be small. Further details on the physics configuration and experimental set-up are provided in Table 1.
a The domain for two nested experiments and b the zonally uniform prescribed SST (k). The details of the experimental set-up are provided in Table 1
3 The sensitivity of the water cycle to resolution
3.1 Precipitation and moisture budget
Figure 2 shows comparisons of the mean total, convective, and non-convective precipitation averaged zonally over the nested region from the two experiments. The comparison between the high and the low-resolution domains of the nested runs is done over the same area that is covered by the interior of the high-resolution nested domain excluding the lateral boundary adjustment zone, which consisted of 1 specified point and 14 relaxation points. Thus, the large-scale forcings for the two simulations are comparable for this region. The figure shows that total precipitation increases as spatial resolution increases, with the resolved precipitation (non-convective, from microphysics) increasing while convective precipitation decreases with increased spatial resolution. Precipitation is particularly sensitive at the finer resolution; precipitation almost doubles as the grid spacing goes from 0.2° to 0.04°.
A moisture budget analysis is performed to study the dependence of the total water cycle on model resolution and to quantify the roles of eddy fluxes and the contribution of upscale feedbacks to the transport of mean moisture by the mean circulation. First, a comparison between the CRM and HRTCM simulations is considered. The moisture budget equation for HRTCM is given by
where \( \bar{v}_{3d} \) and \( \bar{q} \) are the three dimensional wind vector and water vapor mixing ratio at the resolution of HRTCM (0.2°). The three terms on the RHS of Eq. (1) represent atmospheric sources of water vapor (sinks if negative) due to microphysics (resolved condensation), cumulus parameterization, and the planetary boundary layer parameterization. For the CRM the equivalent equation is
Here \( \bar{v}_{3d} \) and \( \bar{q} \) are averages of the CRM grid points collocated within each HRTCM grid point, i.e., an average of the 5 by 5 block of CRM grid points that align with a corresponding HRTCM grid point. The mean moisture flux on the LHS of Eq. (2) is calculated by applying the advection routine on the coarsened fields, with the results having the same resolution as the LHS of Eq. (1). The moisture flux contributed by the range of scales between the fine and coarse grid resolutions is represented by the third term on the RHS of Eq. (2).
Figure 3 compares the terms in Eqs. (1) and (2). Note that \( Q_{cupara} \) and \( Q_{pbl} \) are combined into \( Q_{para} \) for brevity since both involve eddy transport of unresolved scales. Note that \( Q_{cupara} \) is zero for CRM since it does not use a cumulus parameterization. The transport of mean moisture by the mean circulation is deeper at higher resolution when comparing the CRM and HRTCM simulations, as indicated by the moisture transport by the mean flow, with peak convergence at 600 hPa for CRM and 750 hPa for HRTCM. This suggests a positive “upscale dynamical effect” by the smaller scales that strengthens convection. Specifically, at higher resolution the addition of the small scale clouds and motions that cannot be resolved in the coarse simulation generates additional mid-level heating that results in an overall increase in mean vertical moisture transport. This is consistent with the elevated microphysical drying (Fig. 3b) and associated heating (not shown). The increased tropospheric microphysical drying in CRM is balanced by the moistening due to the resolved eddy fluxes that transport moisture from the boundary layer to the troposphere (Fig. 3c). The eddy transport moisture from regions of evaporation to those of precipitation and dry the boundary layer. The response in the boundary layer to this drying is shown in Fig. 3d. The flux of moisture from the boundary layer to the upper troposphere increases the surface evaporation as well as precipitation.
A similar comparison is performed on the moisture budgets of TCM and HRM. In this case \( \bar{v}_{3d} \) and \( \bar{q} \) in HRM are averages over the grid size of TCM, so the HRM budget contains an additional term, similar to the last term in RHS of Eq. (2) that represents moisture transport by eddies resolved by the 0.2° grid spacing of HRM but not by the 1.0° grid-spacing of TCM. Both simulations contain the drying by the cumulus parameterization. Fig. 4a shows the comparison of the convergence of mean moisture by the mean circulation in HRM and TCM. The total moisture convergence from the two cases is comparable, with only a relatively small, negative upscale effect. At the higher resolution (HRM), the convergence of mean moisture by the mean circulation has slightly decreased at low levels compared to TCM. The resolved microphysical drying increases with resolution especially above 800 hPa as more moisture is supplied by the eddies (Fig. 4c) which dry the boundary layer in the process. This in turn increases the surface evaporation (Fig. 4d). The drying by the cumulus parameterization remains almost unchanged by the increased resolution (Fig. 4d).
3.2 Parameterized versus required drying
In the last subsection it was shown that the effects of increased resolution can be quantified by the eddy processes that transport moisture from the boundary layer to the free troposphere, and subsequently increasing the resolved precipitation. Ideally the suite of physics parameterizations in the model would account for this resolution sensitivity so that the results of model simulations, specifically total precipitation (drying) and the mean (resolved) moisture transport, would not change as the spatial resolution changes. Much of this adaption would presumably need to occur in the cumulus parameterization, since it is the main contributor to the handling of subgrid moisture transport above the boundary layer. The difference between the required parameterization drying and the actual model parameterized drying represents the scale-induced parameterization error of the model, i.e., the deviation from its higher resolution counterpart.
For the simulated water cycle to be resolution independent, the moisture transported by the mean (resolved) flow from HRTCM and CRM have to be equal over the area of each HRTCM grid column (\( \nabla \cdot \left( {\bar{v}_{3d} \bar{q}} \right)^{HRTCM} = \nabla \cdot \left( {\bar{v}_{3d} \bar{q}} \right)^{CRM} \)). The extent to which this equality fails represents the resolution dependence of the model. Therefore, from Eqs. (1) and (2),
where Q required is the required moisture source term to achieve scale invariance for the given set of physics parameterizations.
Figure 5a compares the required drying, Q required , with the parameterized cumulus drying. While resolution dependence is likely present in the other parameterizations as well, it is presumed that it is greatest in the cumulus scheme since it is responsible for producing the effect of eddies that move moisture from the boundary layer to the free troposphere. Clearly the cumulus parameterization underestimates drying near the surface (below 900 hPa), which is the source region for moisture that should be transported to higher levels. And the cumulus also underestimates drying above 700 hPa where condensational drying should take place. It is possible that the boundary layer parameterization is contributing to some of the differences near the surface, but at higher levels the difference should almost entirely be due to the cumulus scheme. Similar to Eq. (3), the drying required for the moisture transport in TCM to agree with that of HRM is given by
The comparison of this required drying with the cumulus parameterization is shown in Fig. 5b. Once again the parameterization underestimates the drying significantly especially near the surface, but above the boundary layer it is comparable to the required drying.
4 Behavior of moisture transport across scales
As was shown in the previous section, the improper representation of moisture transport by eddy fluxes causes resolution dependence for the water cycle in the model. The resolution induced error generated by a set of parameterizations needs to be corrected. And, one can potentially use the information within the resolved scales to add an adjustment term for this purpose. In this section, the behavior of the moisture transport at various scales, and co-variability of eddy fluxes at adjacent ranges of scales, is studied to explore the potential for representing unresolved eddy fluxes in terms of their resolved counterparts. The one-to-five ratio between the grid spacings of the parent and nested domains allows the calculation of moisture transport at intermediate scales. For CRM, which has a grid spacing of 0.04°, one can average the simulation over a five by five box of grid points to estimate what would be represented at 0.20° grid spacing, and over a three by three box of grid points to estimate the representation at 0.12° grid spacing. Similarly, one can estimate the moisture transport at 1.00 and 0.60 grid spacing from HRM, and at 5° and 3° grid spacing from TCM. The maximum upward moisture flux is calculated by vertically integrating the moisture divergence [LHS of Eqs. (1) and (2)] from the surface to the level at which the convergence changes sign from negative to positive.
Figure 6 shows the dependence of the maximum upward moisture flux on resolution for the various simulations over the overlapping portion of the domains. For all cases, the maximum upward transport of moisture increases with spatial resolution. The mean upward moisture transport at 0.2° for CRM is larger than that of HRTCM, which as noted above, indicates that resolving the small scale motions not only enhances transport by those newly resolved motions but also the transport by the already resolved large-scale circulation. In contrast, the mean upward moisture transport at 1.0° for HRM is smaller than that of TCM because of the negative upscale effect at these grid spacings, as discussed above. The opposite scale effect between the two pairs of simulations demonstrates the difficulty in dealing with the parameterization scale dependence. The behavior can change at different resolutions, and the resolution induced bias does not always change monotonically with grid spacing.
If, as shown above, the moisture transport increases with increasing resolution, one can ask if there is significant spatial and temporal relationship between eddy fluxes resolved by adjacent ranges of scales. In other words, can one use the smallest resolved eddies to parameterize the moisture transport by the even smaller unresolved eddies within a limited range of scales?
From a mathematical point of view, consider the eddy moisture flux divergence F(k) associated with eddies over a continuum of wave numbers between k 1 and k:
and suppose k r is a wave number between k 1 and k 2, which represents a particular model grid spacing. Therefore, for a narrow range of scales, \( \nabla \cdot (\overline{{v_{3d}^{\prime } q^{\prime } }} )_{{k_{r} \leftrightarrow k_{2} }} \) (the moisture transport by unresolved eddies) is approximated by
Once again for the narrow range of scales, we can assume that \( \frac{\partial F}{\partial k} \) remains constant between k 1 and k 2, so it can be calculated as
Substituting Eq. (7) into Eq. (6)
In other words, one can expect some correlation between the divergence of eddy moisture fluxes that are resolved by a certain grid spacing and those resolved by a finer grid spacing, assuming the change in resolution is sufficiently small.
Figure 7a shows the correlations between the divergences of eddy fluxes resolved over the range of 0.20° to 0.12° grid spacing and those between 0.12° to 0.04° grid spacing from the CRM simulation. The correlation is larger in regions away from strong precipitation such as at the upper levels (which are generally dry) and close to the surface. In general the correlations is 0.5 and above suggesting some potential for using the marginally resolved eddy fluxes to represent the unresolved eddy fluxes at this range of scales. Fig. 7b shows correlation between the divergences of eddy fluxes resolved over the range of 1.0°–0.60° grid spacing and those between 0.60° and 0.20° grid spacing from the HRM simulation. The correlations are much weaker, which is not surprising given the wide range of scales involved. The large values of correlation in the boundary layer over regions of evaporation points to the potential for representing the boundary layer drying by unresolved eddies using those that are resolved. This could reduce the sensitivity of evaporation and precipitation to spatial resolution.
5 Discussion
This study examines the role of eddies in the sensitivity of the regional water cycle to changes in spatial resolution for a pair of aquaplanet regional model simulations. This idealized setup excludes the effects of topography and land cover that would normally complicate resolution comparisons. The pair of nested experiments is designed to cover a wide range of scales. In the first experiment, a cloud resolving domain (0.04° horizontal grid spacing) is one-way nested in a tropical channel simulation with 0.2° grid spacing. In the second experiment, a regional domain with 0.2° grid spacing is one-way nested in a tropical channel with 1.0° grid spacing.
A moisture budget analysis is performed at multiple scales to quantify the contribution of eddy fluxes to resolution differences. Increased resolution increases eddy transport of moisture from the boundary layer to the mid troposphere. A change from 0.2° to 0.04° grid spacing doubles the total upward moisture flux (Fig. 6a) and precipitation (Fig. 1a) at the 0.2° grid scale through a positive upscale feedback on the mean moisture transport. In contrast, changing from 1.0° to 0.20° grid spacing increases the total upward moisture flux relatively modestly because of increased eddy fluxes and negative feedback on to the mean upward transport (Fig. 6b). In general, an increase in spatial resolution is accompanied by an increase in the eddy moisture flux divergence, which leads to an increase in the resolved (microphysical) precipitation and surface evaporation (Figs. 3, 4), which in turn is caused by increased moisture transport from the boundary layer to the free troposphere.
If one assumes the cumulus parameterization should have the largest role in compensating for scale induced changes to the moisture budget, one can compare the strength of the cumulus effect at different resolutions with the adjustment that would be necessary to obtain scale independent results. This comparison has been done, and the results differ between the two experiments. In the comparison between CRM and HRTCM, the parameterization underestimates the magnitude of the drying at all levels, in general, and to a larger extent near the surface where eddy fluxes dry the boundary layer (Fig. 5a). However, the comparison between HRM and TCM gives a different result, with the parameterization underestimating the drying within the boundary layer like the other experiment, but is comparable to the required drying at higher levels. The sign is even different for some mid-cloud levels.
Co-variability of the divergence of eddy moisture fluxes among adjacent ranges of scales is also investigated. Within the boundary layers for regions with evaporation, the moisture transported by eddies at scales ranging between \( 0.2^\circ \leftrightarrow 0.12^\circ \) and \( 0.12^\circ \leftrightarrow 0.04^\circ \) are correlated \( (corr \ge 0.7) \), which suggests a potential for representing unresolved eddy transport of moisture at the cloud resolving scale by resolved ones at the mesoscale. This could be used to reduce the sensitivity of the simulated hydrological cycle to spatial resolution. The correlation between the moisture transports by eddies in the range of \( 1.0^\circ \leftrightarrow 0.6^\circ \) and \( 0.6^\circ \leftrightarrow 0.2^\circ \) is, however, relatively small, indicating the difficulty in representing unresolved eddy moisture transport at the mesoscale by resolved ones at the larger scale. This can be expected from the nature of cloud organization. For the smaller grid spacings, the comparisons are basically between scales where clouds form and dissipate and mesoscale organization plays a minor role. However, the larger grid spacing comparison involves scales that are strongly controlled by mesoscale organization and much less by random cloud formation. In applying these results to reduce the sensitivity of the water cycle to spatial resolution, one could calculate fluxes at the scale of the given model grid and also at a coarser grid spacing based on the same meteorological state. Then, one could use the difference between the two to represent the fluxes by the unresolved eddies and use this information as an additional correction term when integrating the model in time.
In summary, the sensitivity of the water cycle to spatial resolution, which stems from the inadequacy of the physics parameterizations in representing eddy transport of moisture, remains an important challenge that needs to be addressed, or at least constrained and quantified, so that the benefits of multi-resolution grids can be realized.
References
Arakawa A, Schubert WH (1974) Interaction of a cumulus cloud ensemble with the large-scale environment, Part I. J Atmos Sci 31:674–701
Arakawa A, Jung J-H, Wu C-M (2011) Toward unification of the multiscale modeling of the atmosphere. Atmos Chem Phys 11:3731–3742. doi:10.5194/acp-11-3731-2011
Boyle J, Klein SA (2010) Impact of model horizontal resolution on climate model forecasts of tropical precipitation and diabatic heating for the TWP-ICE period. J Geophys Res 115:D23113. doi:10.1029/2010JD014262
Castro CL, Pielke RA Sr, Leoncini G (2005) Dynamical downscaling: assessment of value retained and added using the regional atmospheric modeling system (RAMS). J Geophys Res 110:D05108
Collins WD et al (2004) Description of the NCAR community atmosphere model (CAM 3.0), NCAR Technical Note NCAR/TN-464+ STR. National Center for Atmospheric Research, Boulder, Colo
Gent PR, Yeager SG, Neale RB, Levis S, Bailey DA (2009) Improvements in a half degree atmosphere/land version of the CCSM. Clim Dyn 34(6):819–833. doi:10.1007/s00382-009-0614-8
Giorgi F, Marinucci MR (1996) Improvements in the simulation of surface climatology over the European region with a nested modeling system. Geophys Res Lett 23(3):273–276. doi:10.1029/96GL00050
Hagos S, Leung L, Rauscher S, Ringler T (2013) Errors characteristics of two grid refinement approaches in aqua-planet simulations: MPAS-A and WRF. Mon Weather Rev. doi:10.1175/MWR-D-12-00338.1
Holtslag AAM, Boville BA (1993) Local versus nonlocal boundary-layer diffusion in a global climate model. J Clim 6:1825–1842
Jung J-H, Arakawa A (2004) The resolution dependence of model physics: illustrations from nonhydrostatic model experiments. J Atmos Sci 61:88–102
Jung T et al (2012) High-resolution global climate simulations with the ECMWF model in project Athena: experimental design, model climate, and seasonal forecast skill. J Clim 25:3155–3172
Lau N-C, Ploshay JJ (2009) Simulation of synoptic- and subsynoptic-scale phenomena associated with the East Asian summer monsoon using a high-resolution GCM. Mon Weather Rev 137(1):137–160
Leung LR, Qian Y (2003) The sensitivity of precipitation and snowpack simulations to model resolution via nesting in regions of complex terrain. J Hydrometeorol 4:1025–1043
Mizuta R et al (2006) 20-km-mesh global climate simulations using JMA-GSM model-mean climate states. J Meteor Soc Jpn 84:165–185
Neale RB, Richter JH, Jochum M (2008) The impact of convection on ENSO: from a delayed oscillator to a series of events. J Clim 21:5904–5924
Randall DA (1996) Parameterizing fractional cloudiness produced by cumulus detrainment. In: Proceedings of the workshop on cloud microphysics parameterizations in global atmospheric circulation models, WMO/TD-No, vol 713, pp 1–16
Rasch PJ, Kristj′ansson JE (1998) A comparison of the CCM3 model climate using diagnosed and predicted condensate parameterizations. J Clim 11:1587–1614
Ray P, Zhang C, Moncrieff MW, Dudhia J, Caron J, Leung LR, Bruyere C (2011) Role of the atmospheric mean state on the initiation of the Madden-Julian oscillation in a tropical channel model. Clim Dyn 36:161–184. doi:10.1007/s00382-010-0859-2
Richter JH, Rasch PJ (2008) Effects of convective momentum transport on the atmospheric circulation in the community atmosphere model, version 3. J Clim 21:1487–1499
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Barker DM, Duda MG, Huang X-Y, Wang W, Powers JG (2008) A description of the advanced research WRF Version 3. NCAR Technical Note, NCAR/TN–475+STR
Zhang GJ, McFarlane NA (1995) Sensitivity of climate simulations to the parameterization of cumulus convection in the Canadian Climate Centre general circulation model. Atmos Ocean 33:407–446
Acknowledgments
This work is supported by the Regional and Global Climate Modeling Program of the US Department of Energy Biological and Environmental Research Program. Dr. Gustafson is supported by a DOE Early Career Research and Dr. Singh is supported by Pacific Northwest National Laboratory’s Laboratory Directed Research and Development (LDRD) program. Computing resources are provided by the National Energy Research Scientific Computing Center (NERSC) and National Center for Computational Sciences (NCCS) through the INCITE Climate End Station project. Pacific Northwest National Laboratory is operated by Battelle for the U.S. Department of Energy under Contract DE-AC06-76RLO1830.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Hagos, S., Leung, L.R., Gustafson, W.I. et al. Eddy fluxes and sensitivity of the water cycle to spatial resolution in idealized regional aquaplanet model simulations. Clim Dyn 42, 931–940 (2014). https://doi.org/10.1007/s00382-013-1857-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-013-1857-y