Abstract
Underestimated rainfall over Amazonia was a common problem for the Coupled Model Intercomparison Project phase 3 (CMIP3) models. We investigate whether it still exists in the CMIP phase 5 (CMIP5) models and, if so, what causes these biases? Our evaluation of historical simulations shows that some models still underestimate rainfall over Amazonia. During the dry season, both convective and large-scale precipitation is underestimated in most models. GFDL-ESM2M and IPSL notably show more pentads with no rainfall. During the wet season, large-scale precipitation is still underestimated in most models. In the dry and transition seasons, models with more realistic moisture convergence and surface evapotranspiration generally have more realistic rainfall totals. In some models, overestimates of rainfall are associated with the adjacent tropical and eastern Pacific ITCZs. However, in other models, too much surface net radiation and a resultant high Bowen ratio appears to cause underestimates of rainfall. During the transition season, low pre-seasonal latent heat, high sensible flux, and a weaker influence of cold air incursions contribute to the dry bias. About half the models can capture, but overestimate, the influences of teleconnection. Based on a simple metric, HadGEM2-ES outperforms other models especially for surface conditions and atmospheric circulation. GFDL-ESM2M has the strongest dry bias presumably due to its overestimate of moisture divergence, induced by overestimated ITCZs in adjacent oceans, and reinforced by positive feedbacks between reduced cloudiness, high Bowen ratio and suppression of rainfall during the dry season, and too weak incursions of extratropical disturbances during the transition season.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The Amazonian rainforest accounts for approximately 15 % of global terrestrial photosynthesis (Field et al. 1998) so that future changes of rainfall in that region are needed for determining global carbon-climate feedbacks (Cox et al. 2004). However, CMIP3 models were shown to have highly variable biases in Amazonia precipitation and its seasonality (Li et al. 2006; Vera et al. 2006). Such biases and lack of understanding of their cause contribute to the large uncertainty in projecting future changes of the atmospheric CO2 concentration and climate (Friedlingstein et al. 2006).
Since the Intergovernmental Panel on Climate Change (IPCC) Fourth Assessment Report (AR4), considerable efforts have been made to reduce dry biases in the climate models that participated in the IPCC Fifth Assessment Report (CMIP5) (Dickinson et al. 2006). CMIP5 includes more than 50 models from 24 modeling groups with generally higher resolution and more ensemble members for individual experiments (Taylor et al. 2012). Are rainfall climatology, variability and their controlling processes realistically represented in CMIP5 models? If not, what are the main causes of such model biases?
What metrics should we use for model evaluation? The CMIP5 program has recommended a broad suite of metrics for characterizing general model performance (Gleckler et al. 2008). However, because this study is focused on the evaluation of rainfall biases over Amazonia and their underlying causes, it uses a process-based model evaluation.
Since IPCC AR4, our understanding on what control climatology and variability of Amazonian rainfall has advanced significantly. We take advantage of these recent improvements, as well as knowledge accumulated earlier, in determining the metrics. In particular, it has been established that SST anomalies over the adjacent tropical oceans are the primary forcing for drought and extreme events in some part of Amazonian basin (Chen et al. 2011; Davidson et al. 2012; Doi et al. 2012; Liebmann and Marengo 2001; Moura and Shukla 1981; Bombardi and Carvalho 2011), through their impacts on atmospheric circulation patterns and moisture transport (Wang and Fu 2002; Fu et al. 1999). Surface soil moisture and vegetation feedbacks, as well as land, regulate rainfall variability by altering the surface Bowen ratio and buoyancy of air in the boundary layer (Nepstad et al. 1999; Malhi and Wright 2004; Fu and Li 2004; Chen et al. 2011; Lee et al. 2011; Toomey et al. 2011). While both remote and local effects as mentioned above are important, their relative importance can change in different seasons (Seth et al. 2011).
This study evaluates eleven CMIP5 models and determines what biases in Amazonian rainfall and its seasonality still remain. It analyzes sea surface temperature (SST) and regional land surface forcing and their influences on precipitation to determine the possible causes for rainfall bias in different seasons and regions. The climate records over Amazonia are too short for evaluation of the sensitivity of rainfall to the warming trend of global SST even though its simulation is important for determining the fidelity of the climate projection. We also evaluate the partitioning between convective and large-scale precipitation because they are parameterized based on different large-scale conditions in models and can impact surface water partitioning between evapotranspiration (ET), infiltration, and runoff.
Section 2 describes the datasets, models and analysis methods used in this study. Section 3 reports the results of our analysis in detail for specialized readers. A brief summary of the main findings is provided at the end of each sub-section for general readers.
2 Data and methods
2.1 The CMIP5 simulations
This study examines the precipitation simulated in the historical runs of CMIP5 models and other key variables, a total of eleven models are available at this time. A general description is given in Table 1. These simulations were performed by different modeling groups that participated in the CMIP5, organized by the World Climate Research Programme’s (WCRP) Working Group on Coupled Modelling (WGCM) and to be addressed in the 5th Assessment Report (AR5) of the IPCC. All the models provided multiple ensemble runs in order to increase the signal-to-noise ratio except for GFDL-ESM2M and INM-CM4, and we average all the ensemble runs before comparing to observations. Models with fewer ensemble members will have more uncertainty due to random internal variability of the models (Deser et al. 2010). More details on the dynamic core and physical parameterization of these models and description of performed simulations can be found in corresponding references. The model outputs are being archived and made available to the scientific community by the Program Climate Model Diagnosis and Intercomparison (PCMDI) at their website: http://pcmdi3.llnl.gov/esgcet/home.htm;jsessionid=8B859722DD0B923B9E05C171806B87A4.
Some modeling groups provide a new set of models named Earth System Models (ESMs), which are atmosphere-ocean global climate models (AOGCMs) coupled to a carbon cycle model (Flato 2011). Simulations are run in various spatial resolutions. We interpolate different resolutions into 2.5° × 2.5° in order to minimize effects of resolution on our comparison. To reduce the noise in modeled rainfall, we use pentad-averaged precipitation derived from daily means for precipitation to assess its frequency distribution. For other fields, monthly data are employed to provide a reasonably comprehensive picture of model performance.
The historical experiment, which resembles the twentieth century simulation in CMIP3, is carried out with all forcing including changes of atmospheric composition due to anthropogenic and volcanic influences, solar forcing, aerosol emissions and land use change (Taylor et al. 2012). The simulations are initialized using pre-industrial conditions of 1850 and carried out to 2005. We use the time period of 1979 to 2005 for most fields, a period when the observational record is most reliable and available. The analysis of sea surface temperature (SST) is carried out for the period of 1950 to 2005 to adequately capture the modes of lower frequency SST variability.
2.2 Reference data
Beginning from 1979, satellite-based measurements along with ground-based observations substantially improved spatial and temporal sampling and reliability of the reanalysis products, supporting our choice of 1979–2005 periods for model evaluation.
The Global Precipitation Climatology Project (GPCP) provides combined precipitation products (Adler et al. 2003). Since GPCP daily precipitation only starts from 1992 and in order to include as many years as possible, we use the GPCP v1.2 pentad product (Xie et al. 2003) to assess the frequency distribution. Monthly CPC merged analysis of precipitation (CMAP) is also employed as another reference for the Taylor diagram. Many studies have compared these precipitation products (Shin et al. 2011), including over South America (Negrón Juárez et al. 2009).
The ECWMF ERA-Interim reanalysis data (Dee et al. 2011) has been demonstrated to be able to capture the ITCZ compared with observations (Žagar et al. 2011), and is also the best among the three state-of-art reanalysis products for the Amazonian region (Lorenz and Kunstmann 2012). Since the ERA-Interim has a reasonable terrestrial water balance, we assume that it has a better estimation of convective and large-scale precipitation than models, even though it is still quite uncertain. Other variables examined are mainly from the ERA-Interim, including winds, surface latent and sensible heat fluxes, surface solar radiation, geopotential height and water vapor transport.
We use the NOAA/NCDC Extended Reconstructed SST (ERSST) version 3b (Smith et al. 2008), available from 1854 to present. It is derived from the International Comprehensive Ocean-Atmosphere Data Set (ICOADS) data with missing values filled in by statistical methods. SST in this dataset since 1950 is compared to that of models in order to provide enough sample years to reduce measurement biases and uncertainties. The models with tripolar gridded SSTs have been interpolated into a common lat-lon grid with spatial resolution of 2.5° × 2.5°.
Shortened names are used for observations in the figures. If more than one datasets are used, we chose one dataset as the reference data and compared the other datasets to assess observational uncertainty.
2.3 Computation of variables and indices
To investigate the potential causes of precipitation bias, we will analyze whether atmospheric circulation, surface conditions or Pacific and Atlantic SSTs are reasonably simulated in these models. The variables we evaluate include the lower and higher tropospheric winds, 500 hPa geopotential height, surface fluxes, moisture convergence and SST indices.
Due to lack of instantaneous wind and atmospheric humidity information in the CMIP5 models outputs, we compute moisture convergence from the water budget (Trenberth et al. 2007) instead of the vertical integration of horizontal moisture transport, using the following equation:
where MC is moisture convergence, P is precipitation, E is evapotranspiration, and ΔTWV is the change in atmospheric total water vapor storage. Some models do not provide evapotranspiration, so E is calculated as:
where λ = 2.502 × 106 J kg−1 is latent heat of vaporization, and LH is upward surface latent heat flux.
To quantify the effects of teleconnection, several SST indices are calculated. The Niño 3 index is an average of SST anomalies (SSTA) in the region of 150°W–90°W and 5°N–5°S, and Niño 4 index is an average of SSTA in the region of 160°E–150°W and 5°N–5°S. The Atlantic Multidecadal Oscillation (AMO) is described as the area weighted average of SSTA over the northern Atlantic, basically from 0 to 70°N (Endfield et al. 2001). The detailed calculation procedure is found on the NOAA/ESRL website: http://www.esrl.noaa.gov/psd/data/timeseries/AMO/. The tropical Atlantic SST gradient (AtlG) is defined as the area averaged SSTA difference between the northern (60°W–30°W, 5°N–25°N) and southern (30°W–0°, 5°N–25°N) Atlantic (Giannini et al. 2004), and is important for the cloudiness in some regions of Amazonia (Arias et al. 2010).
3 Results
3.1 Comparisons of rainfall seasonality
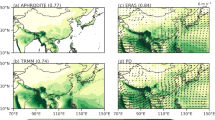
Figure 1 shows the spatial pattern of the seasonal mean total rainfall, convective and large-scale precipitation of the eleven models in northern South America. Total rainfall is compared with GPCP, and convective and large-scale rainfall is compared with ERA-Interim reanalysis (ERA-Int). Most models generally show reasonable patterns of seasonal precipitation (Fig. 1a). During the wet seasons (DJF and MAM), three Had-models, MPI-ESM and IPSL can adequately simulate the rainfall patterns over the Amazon basin. Maximum rainfall centers in the two GISS models are too far northward and that modeled by CCSM4 is too far eastward. INM-CM4 has enough rainfall over tropical South America but less in its central region.
In the dry season (JJA), only the two HadGEM2 models can capture the center of rainfall over the northwest corner of South America (Fig. 1a). Most of the models overestimate rainfall associated with the Atlantic ITCZ, especially the two GISS, two HadGEM and IPSL models. During the transition season (SON), the three Had-models and MPI-ESM capture the northwest-to-southeast spread of rainy area fall pattern as observed. CCSM and GFDL-CM3 also capture this rainfall pattern, but underestimate rainfall amounts. GFDL-ESM2M and IPSL show rainfall patterns similar to those of the dry season, thus substantially underestimating rainfall over southern Amazon. The majority of the models either overestimate the Atlantic ITCZ (the two GISS models) or the eastern Pacific ITCZ (MPI) or both (CCSM4, the two GFDL models, the three Had- models and IPSL). Such an overestimate of the ITCZs could enhance subsidence and moisture divergence over the Amazon, contributing to dry biases during the dry season. This problem also exists in CMIP3 models, showing that a misrepresentation of the tropical ITCZ can result in a bias in the annual cycle of precipitation over the Amazon (Bombardi and Carvalho 2009).
Most of the other models overestimate convective rainfall and underestimate large-scale rainfall during the wet seasons, but underestimate both convective and large-scale rainfall in the dry and transition seasons (Fig. 1b, c). CCSM4 is among the best in simulating convective and large-scale precipitation for all the seasons. The three Had-models strongly overestimate convective rainfall and underestimate large-scale rainfall in SON. The two GISS models substantially underestimate convective rainfall and overestimate large-scale rainfall in all four seasons (Fig. 1b, c).
To quantify the precipitation bias in Amazonia, we select four regions: the southern Amazon (Sama, 70°W–50°W, 15°S–5°S), northern Amazon (Nama, 70°W–55°W, 5°S–5°N), northwestern Amazon (NWama, 75°W–60°W, 10°S–5°N), and South American Monsoon System region (SAMS, 60°W–45°W, 17.5°S–5°S) shown in Fig. 2a. The southern Amazon has a wet season beginning in austral spring, peaking in summer and ending in austral fall (Marengo et al. 2001; Li and Fu 2004), while the northern Amazon differs in rainfall seasonality since it crosses the equator (Marengo 2005; Wang and Fu 2002). The northwestern Amazon is also an extension of the V index region, which was defined to describe the moisture transport from the equator to the southern Amazon (Wang and Fu 2002; Petersen et al. 2006). The South American Monsoon System region is very closely related to the South Atlantic Convergence Zone (SACZ; Vera et al. 2009).
Rainfall seasonality is stronger in Sama and SAMS than in Nama and NWama (Fig. 2b). Over Sama and SAMS, the wet seasons are DJF and MAM, and the dry and transition seasons are JJA and SON. In the wet seasons, the difference in precipitation across the models is not as significant as in dry seasons. Most models produce reasonable rainfall with mean biases ranging from −1.5 to 1.2 mm day−1. In the dry seasons, CCSM4, HadGEM2-CC, HadGEM2-ES and INMCM4 best simulate precipitation while HadCM3, GFDL-CM3, GFDL-ESM2M and IPSL significantly underestimate it. Indeed, GFDL-ESM2M and IPSL have no rain in JJA in Sama. Rainfall has the largest discrepancies between models in transition seasons due to the strong dry biases in the two GFDL models, IPSL and the two GISS models.
Over Nama and NWama, seasonal rainfall in CCSM4, the two GISS models, and the three Hadley models generally agree with observations. The two GFDL models, HadCM3 and IPSL show dry biases in rainfall by 3–4 mm day−1 (25–30 %) over the wet season and by as much as 4–5 mm day−1 (50–80 %) during the dry season.
Generally, models tend to have reasonable standard deviations compared with GPCP in Nama and NWama, even those models (the two GFDL models, MPI-ESM, IPSL) with a dry bias in the mean rainfall of dry season. For the latter models, dry season rainfall can be zero in Sama and SAMS in the interannually dry years.
Figure 3 shows the distribution of rainrate derived from pentad rainfall in the four regions. Results for the GISS-E2-H model are not shown because it does not provide daily precipitation. GFDL-ESM2M and IPSL both strongly overestimate the frequency of occurrence of pentads with no rain in the four regions (>50 % in Sama and SAMS, >40 % in Nama and >35 % in NWama). They also have fewer pentads of strong precipitation (>10 mm day−1 in a pentad) in Nama and NWama. GFDL-CM3 shows more pentads of no rain, but has a reasonable simulation of medium precipitation (>5 and <10 mm day−1 in a pentad) for Sama and SAMS.
No models realistically represent the observed distribution pattern of rainrates. The three Had-models overestimate medium rainrate and underestimate light rainrate, whereas the two GFDL models, CCSM, and IPSL underestimate medium rainrate over all four regions. The overestimate of light rainrate in the two GFDL models is similar to that in GFDL-CM2.0 (Dai 2006; Sun et al. 2006), while GFDL-CM3 has largely improved its medium to strong rainrate (1–10 mm day−1) in Sama and SAMS compared to the old version (Sun et al. 2006). CCSM4 is reasonable for Nama and NWama, but shows more non-rain pentads for Sama and SAMS. INM-CM4 is among the best for Sama and SAMS, but shows more pentads with medium and strong rainfall in Nama and NWama. The GISS models, similar to the old one GISS-ER (Sun et al. 2006; Dai 2006), underestimate medium and strong rainrate over the southern Amazon but overestimate it over tropical South America.
Taylor diagrams (Taylor 2001) are used to compare model performances for the annual cycle of precipitation with observations (Fig. 4). Overall, the models produce better annual cycles of precipitation in Sama and SAMS than in Nama and NWama. Rainfall has clear one cycle during a year in Sama and SAMS (Fig. 2b). Therefore, the correlations between the models and observation in Sama and SAMS are larger than 0.9. Two HadGEM2 models (‘G’ and ‘H’) have the least mean square error (MSE) in Sama, NWama and SAMS, though they underestimate the standard deviation for NWama. CCSM4 and INM-CM4 (‘A’ and ‘K’) are also among the best in Sama. CCSM4 variability is similar to that of GPCP in all regions except SAMS. Although the two GISS models (‘D’ and ‘E’) perform well in the Sama and SAMS regions, they are among the most poorly performing models in Nama and NWama. The two GFDL models and IPSL (‘B’, ‘C’ and ‘J’) also have large discrepancies in Sama and SAMS. IPSL has the least MSE in Nama. The larger standard deviation of GFDL-ESM2M in all the four regions is dominated by the dry bias during its dry and transition seasons.
Figure 5 compares the partitioning of models between convective and large-scale rainfall for four different seasons and regions. Except for the two GISS models, they generally underestimate large-scale rainfall in all seasons and all four regions. Over the Sama and SAMS regions, models generally overestimate convective rainfall during the wet season (DJF and MAM), and underestimate convective rainfall in the dry and transition seasons (JJA and SON), even though most models simulate reasonable total rainfall (Fig. 2b). Over the two northern Amazon regions (Nama and NWama), convective rainfall is generally unbiased except for MAM, during which several models (the three Hadley models and INM-CM4) overestimate convective rainfall (Fig. 5). Among all the models, the partitioning between convective and large-scale rainfall in CCSM4 agrees the closest to that of ERA-Int.
In short, the eleven CMIP5 models we evaluated generally capture realistically wet season rainfall amounts, although they overestimate convective rainfall and underestimate large-scale rainfall. Over the dry and transition seasons, most of the models underestimate rainfall over the four regions, i.e., except for HadGEM2-CC, HadGEM-ES, and INM-CM4, but overestimate rainfall associated with the Atlantic and eastern Pacific ITCZ. The low biases are stronger in Sama and SAMS, and weaker in Nama and NWama. Greatest inter-model discrepancy occurs in the transition season for all four regions. Both large-scale and convective rainfalls are underestimated.
3.2 Evaluation of surface energy and water balance and atmospheric circulation
A bias of its Atlantic ITCZ in a coupled model could result in a dry bias during the dry season in Amazonia (Doi et al. 2012). A strong Atlantic ITCZ may contribute to large divergence over tropical South America (Rao et al. 1996; Li et al. 2006). In addition, ET influences rainfall change during the transition season in Amazonia (Li and Fu 2004). Therefore, rainfall during the dry and transition seasons is sensitive to land use change or water stress of the rainforest. Since the main source of water for precipitation during dry season is ET and circulation-controlled moisture transport, it is crucial to look at the water budget and determine if either or both are biased in some models.
Figure 6 shows how different models determine rainfall amounts from ET and moisture convergence (MC) in JJA and SON. HadCM3 does not provide the total column water vapor content, so it is not included. Models with more realistic MC and ET generally have more realistic rainfall amounts. Over Sama and SAMS, most models have overestimated moisture divergence during the local dry (Fig. 6a) and transition seasons (Fig. 6b). Models that overestimate moisture divergence the most (MPI-ESM and IPSL or ‘I’ and ‘J’) have the strongest dry bias in rainfall and the lowest ET values. Two GISS models (‘E’ and ‘D’) have reasonable moisture divergence, but they significantly underestimate surface ET and rainfall. Thus, their dry biases are likely caused by either insufficient soil moisture storage and a dry atmospheric boundary layer, or by errors in their convective scheme that underestimates convective rainfall and so causes lower soil moisture and ET (Fig. 1b). GFDL-ESM2M (‘C’) and GFDL-CM3 (‘B’) have biases of MC similar to those of HadGEM2-CC (‘G’) and HadGEM2-ES (‘H’), but much lower ET and rainfall amounts. High ET in the two HadGEM2 models appears to compensate the impact of their excessive moisture divergence, and so they are able to produce realistic rainfall.
In the tropical regions Nama and NWama, about a half of the models overestimate ET, but underestimate moisture convergence and thus rainfall. The two HadGEM2 models overestimate both moisture convergence and ET, thus overestimate rainfall. CCSM4 underestimates MC and overestimates ET during JJA (Fig. 6a). Thus, its dry bias is likely caused by bias of circulation and consequent MC.
Whether an underestimate of MC is caused by an overestimate of the strength of tropical Atlantic and eastern Pacific ITCZ seems to be model dependent. For example, in some models (the two HadGEM2 models and MPI), MC is not underestimated even though the ITCZs are too strong (Figs. 6b, 1a). In other models (CCSM4, the two GFDL models, the two GISS models), MC is underestimated. Thus, too strong ITCZs over adjacent oceans are not always a cause for dry bias of rainfall over Amazonia. MC in the SAMS region is mainly influenced by the South Atlantic Convergence Zone (SACZ; Vera et al. 2009) and is not directly influenced by tropical ITCZs.
Surface conditions are also very important during the dry and transition seasons (Fu and Li 2004). Almost all the models overestimate surface net solar radiation, including the models that overestimate total rainfall (Fig. 7a). This high bias is due to an underestimate of cloudiness, which is also implied by their excessive divergence or weak convergence and their underestimate of large-scale rainfall (Fig. 6). Such a high bias of the surface solar radiation leads to a high bias in surface net radiation (Fig. 7b). Latent flux is generally realistic during DJF and MAM, except for its overestimate by the two GISS models and by INM in all four regions (Fig. 7c). During JJA, latent flux generally agrees with that of reanalysis over Nama and NWama, but is underestimated by 20–40 % in CCSM4, the two GFDL models, the two GISS models, IPSL and INM. During SON, latent flux is underestimated by 20–60 % in the two GFDL models and in MPI and IPSL in all four regions. As expected by surface energy balance, the models that underestimate surface latent flux overestimate surface sensible flux (Fig. 7d), since surface solar flux and net radiative flux (Fig. 7a, b) are overestimated.
To evaluate the role of land surface feedback in determining rainfall during the dry and transition seasons, we evaluate pre-seasonal latent heat versus rainfall to determine sensitivity of rainfall to the land surface. Figure 8a shows that the higher is the JJA latent heat, the larger is the SON precipitation, i.e., the latent flux in the dry season can influence rainfall during the transition season (Li and Fu 2004). In Sama and SAMS, the three Had-models are closest to the observations, whereas GFDL-ESM2M and IPSL show least agreement with observations. In SAMS, the differences in JJA latent heat between the three Had-models are not followed by plausible large differences in SON rainfall, because the occurrence of rainfall is more connected to moisture transport in this monsoon core area. Figure 8b shows a positive correlation between JJA precipitation and SON latent heat even in SAMS, which implies a positive land-atmosphere feedback in coupled models during the dry and transition season.
Figure 9 shows the seasonal mean of the 200 hPa zonal winds. In SON, several models including GFDL-ESM2M, the two GISS models, IPSL and INM-CM4 miss the weak westerly tongue from the tropical Pacific extending to eastern South America. The overestimated westerly winds implies a weaker cold air incursions in these five models, which can contribute to their lack of northwest-southeast advancement of rainfall in SON in these five models.
During DJF, the weak westerly wind area, representing the anticyclonic center, is overestimated over most of the models, except for IPSL, which underestimates the extent of its area. During MAM, the southern hemisphere subtropical jets are realistically represented in GISS-E2R, the three Had models and IPSL. The jets are too poleward in CCSM4, the two GFDL models, GISS-E2H and MPI. During JJA, the southern hemisphere subtropical jets are well represented by most of the models, except for CCSM4 and GFDL-ESM2M.
To summarize our results in this sub-section, the CMIP5 models we evaluated have reasonably well captured the observed large-scale circulation pattern during wet and dry seasons (DJF, MAM and JJA). During SON, i.e., the transition from dry to wet season, the models with large dry biases in rainfall show unrealistically strong 200 hPa westerly zonal winds over Amazonia (GFDL-CM3, GFDL-ESM2M and IPSL), implying weaker incursions of extra-tropical disturbances, which in turn reduce rainfall over the Amazon (Garreaud and Wallace 1998; Li et al. 2006). Surface solar flux and net radiation are overestimated by 10–100 % in most of the models in all seasons over the entire Amazon and SAMS regions, suggesting a significant underestimate of cloudiness and perhaps aerosols. Excessive net radiation is balanced by excessive sensible flux at the surface in most of models, except for the two GISS models. The overestimate of sensible flux is stronger during dry and transition seasons, when latent flux is underestimated in most of the models, except for CCSM, HadGEM2-CC and HadGEM2-ES and INM models. This combination of high bias in surface sensible flux and low bias in surface latent flux leads to strong overestimates of surface Bowen ratio, with convection suppressed during the dry and transition seasons (Li and Fu 2004). The dry biases of rainfall are well correlated with low biases of surface latent flux (or high bias in sensible flux and Bowen ratio) and lack of large-scale moisture convergence in models. Positive correlation between JJA surface latent flux and SON rainfall and JJA rainfall with SON surface latent flux in models suggest that dry biases in surface latent flux soil moisture feedback and rainfall can re-enforce each other through a positive soil moisture feedback.
3.3 Evaluation of rainfall variability and its connection to oceanic forcings
Observations suggest that the influence on rainfall variability, including droughts, over the Amazon by ENSO, the inter-hemispheric SST gradient in the tropical Atlantic and AMO (Moura and Shukla 1981) is mainly during DJF and MAM (Liebmann and Marengo 2001; Marengo et al. 2001). Doi et al. (2012) shows a bias in the Atlantic ITCZ could induce a dry bias in the dry season over the Amazon for the GFDL model. Thus, we evaluate how well the CMIP5 models can simulate the sensitivity of Amazonian rainfall to its oceanic sources of interannual and decadal variability.
Figure 10 shows the correlation between precipitation and Niño 3, Niño 4, AMO and AtlG in the wet seasons (DJF, MAM). Four models (GFDL-ESM2M, HadGEM2-CC and HadGEM2-ES and ISPL) can capture the relationships between precipitation and the Niño 3 and Niño 4 index, respectively. CCSM4 can capture these relationships over Nama (Fig. 10b), but not over NWama (Fig. 10c). However, these models also exaggerate relationships between rainfall in these regions and AMO and AtlG, respectively.
Over Sama, observations show significant correlation during DJF and MAM between rainfall anomalies in this region and the Niño3 index and with AtlG (Fig. 10a). The models (CCSM4, the two GFDL models, and HadCM3) that capture the correlation with ENSO in DJF and MAM, tend to miss the correlation with AtlG, whereas the models that capture the relationship with AtlG (GISS-E2R, HadGEM2-ES, and MPI) tends to miss the correlation with ENSO. Only IPSL and INM capture both of these relationships suggested by observations.
Over the SAMS region, while half of the models (GFDL-ESM2M, HadCM3, HadGEM2-CC, IPSL and INM) capture the correlation between rainfall anomalies in this region and Nino3 in MAM, they exaggerate the relationship in DJF (Fig. 10d). Most of the models capture the relationship in SAMS between rainfall in this region and AtlG.
In general, about half of the CMIP5 models we evaluated (the two GFDL models, the two HadGEM2, IPSL and INM models) capture, but exaggerate, the relationship between the regional rainfall anomalies and the Niño3 and Niño4 indices. The same model groups, along with CCSM4, also capture the relationship between rainfall anomalies over the Sama and SAMS regions and AtlG, but they exaggerate the relationship between rainfall anomalies over northern Amazon (Nama and NWama) and AtlG. Over northern Amazon (Nama, NWama), about half of the models (CCSM4, the two GFDL models, two HadGEM2 models and IPSL) show a spurious relationship between rainfall anomalies and AtlG. Roughly the same group of models (GFDL-CM3, HadGEM2-CC, HadGEM2-ES, MPI, and INM) also shows simply exaggerated relationship between regional rainfall and AMO.
4 Metrics evaluation
This section examines how well the simulation of CMIP5 models compare with observations of rainfall and other variables shown above. To assess the model performance relative to the reference observations, we use simple and popular statistical measures of model fidelity. One is the root-mean square error (RMSE) for a simulated field M corresponding to a reference O (Gleckler et al. 2008). Since the regions in this study are not large enough to get sufficient samples to determine RMSE of spatial pattern, we only use RMSE to account for errors in time series. Therefore, we apply RMSE to the mean seasonal cycle, and it is calculated as follows:
The index t corresponds to the time dimension, and T is the total time steps, i.e., 12 months. In order to have RMSE for all variables on the same scale and to make easy comparisons, Fig. 11 shows by color the rank of RMSE for each variable. Overall, HadGEM2-ES is the best model in most variables especially surface conditions and atmospheric circulation in all the four regions. The smallest errors of these processes could result in its best performance for rainfall simulation. The HadGEM2-ES does not necessarily have the most reasonable SST indices compared with observations, and its relationships between these SST indices and rainfall are not as strong as in some other models. HadGEM2-CC has better surface conditions while its atmospheric circulation and SST indices are worse, which suggests the significance of SST bias on influencing the rainfall simulation. GFDL-ESM2M has overall the largest RMSE for rainfall, both large-scale and convective. GFDL-CM3 and IPSL have large RMSE in Sama and SAMS. Although GFDL-CM3 is reasonable in simulating Niño 4, AMO, AtlG and moisture convergence, some other variables particularly the MC and surface fluxes are not well reproduced.
5 Discussion
5.1 How does CMIP5 perform compared with CMIP3?
Figure 1a shows that most CMIP5 models still have dry bias in the dry season (JJA) as was the case in CMIP3 models. However, we can see that CMIP5 has some improvements. For instance, GFDL-CM3 has increased precipitation in tropical South America compared with the old version GFDL-CM2.0 (Vera et al. 2006), although it is still too dry. This improvement is mainly due to new treatments of aerosol indirect effect and deep and shallow cumulus convection in the new atmosphere model (AM3) (Donner et al. 2011). GFDL-ESM2M, still have a dry bias in the dry season, despite its using a new version of land model. Most CMIP5 models have more annual mean rainfall in the southern Amazon than their CMIP3 versions (Li et al. 2006). The new models also tend to have standard deviations of rainfall more similar to those of the observations (Fig. 2b) than the old ones (Vera and Silvestri 2009), especially in the wet seasons. However, the dry bias in the dry season still remains as the major issue in most of the models. The GISS models still has too strong an Atlantic ITCZ, while they underestimate rainfall amount over central South America throughout the year. IPSL still lacks rainfall in the dry and transition seasons over the southern Amazon, similar to its old version (Vera et al. 2006).
5.2 What causes the dry bias of rainfall over Amazonia in CMIP5 models?
The results in Sect. 3.2 suggest that large-scale circulation in most of the models is generally well simulated over South America during the dry season. Thus, it is probably not the main cause of the dry bias occurring then. Recall that the net surface radiative flux is overestimated all year round, and is balanced by excessive surface latent flux during the wet season. The latter in turn cause excessive soil moisture loss during the wet season, hence reduced soil moisture storage that reduces latent flux and increases sensible flux during the subsequent dry season. These biases of surface latent and sensible fluxes would reduce dry season rainfall, further exacerbating surface dry biases through a positive soil moisture feedback. Dry biases in rainfall, together with underestimated cloudiness, can enhance atmospheric longwave cooling and compensational subsidence, which in turn causes excessive moisture divergence, and further suppresses rainfall. These positive feedbacks between land surface latent flux, rainfall, atmospheric radiation and large-scale circulation are likely responsible for the dry biases in most of the models. Underestimated cloudiness not only initiates these feedbacks during the wet season, but also enhances them during the dry season through increase of surface Bowen ratio and atmospheric radiative cooling.
In the models without dry biases, e.g., HadGEM2-CC, HadGEM2-ES, CCSM and INM, these positive feedbacks were circumvented in part by excessive wet season rainfall, which balances excessive latent flux. In CCSM4, ground water is used to maintain soil moisture storage, which effectively provides an unlimited soil water supply and high latent flux during the dry season.
During the transition season (SON), weak incursions of extratropical fronts, as suggested by excessively strong upper tropospheric westerly winds, likely contribute to the strong dry biases, in addition to the dry biases induced by excessive surface radiation in GFDL-CM3, GFDL-ESM2M, GISS-E2H, GISS-E2R and IPSL.
5.3 Uncertainty of the results
Since rainfall is a non-linear output influenced by various processes including both large-scale and local conditions, biases in the processes could be very crucial for rainfall simulations in the CMIP5 models. Large uncertainties in SST and surface fluxes in Amazonia have been reported for CMIP3 coupled models in previous IPCC AR4 and related studies (IPCC 2007; Li et al. 2006; Yu and Kim 2010), and they still remain in the current generation of GCMs. One way to reduce the noise-to-signal ratio is to run as many ensembles as possible for simulations (Deser et al. 2010). However, due to tremendous expense of running GCMs, not all the centers around the world could finish at least 5 ensembles for a single experiment. Only six out of eleven models in this study, shown in Table 1, give at least 5 ensembles for the historical experiment, and even fewer ensemble members were determined for future projections. Another important limitation is the resolution when it is important for topography and subgrid scale parameterizations. Evaluation of the influence of the uncertainties and differences in model design is beyond the scope of this study.
Several model studies also pay attention to the land use change in Amazonia and its potential influence on rainfall (Lee et al. 2011; Medvigy et al. 2012). For example, Lee et al. (2011) indicates that the vegetation and land use can be more important than remote SST forcing for the rainfall change in the southern Amazon region, particularly in the dry season. Since surface ET is crucial for the wet season onset and rainfall in the dry and transition seasons (Li and Fu 2004), reduced vegetation coverage as a result of land use change could lead to a decrease in surface ET and thus rainfall. While tropical Atlantic warming is demonstrated to be partly responsible for the decrease in dry season rainfall in Amazonia (Marengo et al. 2011), land use change and increased deforestation (Toomey et al. 2011) can exacerbate Amazonian rainfall change and induce more extreme drought events in the twenty-first century. The reasonable incorporation of such regional impacts in the models may improve estimates of the surface moisture and heat flux.
6 Conclusions
We have evaluated the performance of the eleven CMIP5 models for historical rainfall seasonality over Amazonia by comparing them to the GPCP and CMAP rainfall datasets, the ERA-Interim reanalysis product and NOAA/NCDC SST. The results show that the eleven models we evaluated adequately simulate the patterns of annual cycles in Sama and SAMS, but have a large range of performance in Nama and NWama.
The results show that these models generally capture the total rainfall amount during the wet season (DJF and MAM) over the entire Amazon and SAMS. During the dry and transition seasons (JJA and SON), most of the models underestimate total rainfall except for the HadGEM2-CC, HadGEM2-ES, CCSM4 and INM-CM4. The dry biases are strongest in southern tropical South America.
HadGEM2-CC and HadGEM2-ES generally capture the spatial distribution of rainfall over the Amazon basin during all seasons. During the transition season, the three Hadley models, CCSM4 and MPI-ESM realistically capture the northwest-southeast advancement of rainfall in South America that may be linked to the strength and location of subtropical jet, whereas the other models show a dry season rainfall pattern that leads to underestimation of rainfall during the transition season.
Except for the two GISS models (GISS-E2H and GISS-E2R), all others underestimate large-scale rainfall during all seasons. These models generally overestimate convective rainfall during the wet season and underestimate it during the dry and transition seasons. The two GISS models tend to have more large-scale rainfall than convective precipitation, possibly in part due to their lower resolution relative to other models. The two HadGEM2 models realistically capture the distribution of rainrate, as also for CCSM4 and INM-CM4 to a lesser extent. Other models tend to overestimate the occurrence of no rain events and moderate rainrate events. For example, GFDL-ESM2M and IPSL show too many pentads with no rain in the four regions (>50 % in Sama and SAMS, >40 % in Nama and >35 % in NWama), and too few pentads with strong rainfall in Nama and NWama.
Overall, HadGEM2-CC and HadGEM-ES most realistically capture the spatial and seasonal distributions, as well as distribution of rainrate in all the regions of our analysis.
To investigate the possible reasons for rainfall bias in different seasons over Amazonian regions, we have examined surface conditions, atmospheric circulation, SST forcing and water budgets. In the dry and transition seasons, both less moisture convergence or more divergence and lower surface ET are responsible for an underestimate of rainfall. The underestimate of MC by some models (CCSM4, GFDL-CM3, and the two GFDL models) is connected to, and is probably caused by, excessive rainfall over the tropical Atlantic or/and eastern Pacific ITCZs. Other models (the two GISS models for Sama and SAMS) have realistic MC so that low ET accounts for their underestimate of dry season rainfall.
Surface solar and net radiative fluxes are overestimated during all seasons and over all four regions. Surface sensible fluxes are generally overestimated, compensating for their excessive net surface solar radiation and leading to high Bowen ratios. During dry and transition seasons, the high bias in surface sensible flux and Bowen ratio reduces surface latent flux and may suppress rainfall, leading to underestimation.
The westerly 200 hPa zonal wind over the southern Amazon region is excessively strong during the transition season (SON) in some of the models with dry bias that fail to capture the southeast spread of the rainy area (the two GFDL models and IPSL). This connection suggests that these excessively strong westerly winds weaken incursions of the extratropical synoptic disturbance, and so underestimate rainfall during the transition season.
The evaluation of correlation coefficients between regional rainfall anomalies and the interannual and decadal oceanic variability indices suggest that about half of the CMIP5 models (the two GFDL models, the two HadGEM2, IPSL, and INM models) capture, but exaggerate, the relationship between the regional rainfall anomalies and the Niño3 and Niño4 indices. The same groups of models, along with CCSM4, also capture the relationship between rainfall anomalies over Sama and SAMS regions and AtlG, but exaggerate the relationship between rainfall anomalies over the northern Amazon (Nama and NWama) and AtlG, and also show a spurious relationship between rainfall anomalies and AtlG. The rest of CMIP5 models do not show significant correlations between their rainfall variability over Amazonia and the SAMS region, or Niño and AtlG.
We also have used RMSE and correlations to rank model performance for precipitation and related physical processes. HadGEM2-ES outperforms other models in most variables especially surface conditions and atmospheric circulation in all four regions. GFDL-ESM2M has only one ensemble member; thus its has a high RMSE and its output could be dominated by random internal variability.
Dry biases during the dry and transition seasons still exist in the majority of the models and appear to be caused by three factors. First, excessive surface solar radiation, which exists even in the models that overestimate rainfall, persists through all seasons, presumably due to underestimate of cloudiness. During dry seasons, to balance excessive net radiation at the surface, sensible flux, thus Bowen ratio, have to increase. These biases would reduce air buoyancy in the atmospheric boundary layer and suppress convection. Second, in some models, excessively strong ITCZs over the tropical Atlantic and eastern Pacific could cause unrealistically strong moisture divergence and low cloud amounts over Amazonia (e.g., the two GFDL models). These biases would contribute to a dry bias of rainfall in these models. Third, an overestimate of upper tropospheric westerly winds in the two GFDL models and IPSL, may lead to an underestimate of incursions of extratropical synoptic disturbances during the transition season (SON), and cause dry bias in rainfall.
References
Adler RF, Huffman GJ, Chang A, Ferraro R, Xie P, Janowiak J, Rudolf B, Schneider U, Curtis S, Bolvin D, Gruber A, Susskind J, Arkin PA, Nelkin E (2003) The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present). J Hydrometeorol 4:1147–1167
Arias PA, Fu R, Hoyos CD, Li W, Zhou L (2010) Changes in cloudiness over the Amazon rainforests during the last two decades: diagnostic and potential causes. Clim Dyn 37(5–6):1151–1164. doi:10.1007/s00382-010-0903-2
Bombardi RJ, Carvalho LMV (2009) IPCC global coupled model simulations of the South America monsoon system. Clim Dyn 33(7–8):893–916. doi:10.1007/s00382-008-0488-1
Bombardi RJ, Carvalho LMV (2011) The South Atlantic dipole and variations in the characteristics of the South American Monsoon in the WCRP-CMIP3 multi-model simulations. Clim Dyn 36(11–12):2091–2102. doi:10.1007/s00382-010-0836-9
Chen Y, Randerson JT, Morton DC, DeFries RS, Collatz GJ, Kasibhatla PS, Giglio L, Jin Y, Marlier ME (2011) Forecasting fire season severity in South America using sea surface temperature anomalies. Science 334(6057):787–791. doi:10.1126/science.1209472
Collins M, Tett SFB, Cooper C (2001) The internal climate variability of HadCM3, a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 17(1):61–81. doi:10.1007/s003820000094
Collins WJ, Bellouin N, Doutriaux-Boucher M, Gedney N, Halloran P, Hinton T, Hughes J, Jones CD, Joshi M, Liddicoat S, Martin G, O’Connor F, Rae J, Senior C, Sitch S, Totterdell I, Wiltshire A, Woodward S (2011) Development and evaluation of an Earth-system model—HadGEM2. Geosci Model Dev Discuss 4(2):997–1062. doi:10.5194/gmdd-4-997-2011
Cox PM, Betts RA, Collins M, Harris PP, Huntingford C, Jones CD (2004) Amazonian forest dieback under climate-carbon cycle projections for the 21st century. Theor Appl Climatol 78. doi:10.1007/s00704-004-0049-4
Dai A (2006) Precipitation characteristics in eighteen coupled climate models. J Clim 19:4605–4630
Davidson EA, de Araújo AC, Artaxo P, Balch JK, Brown IF, Bustamante C, Coe MT, DeFries RS, Keller M, Longo M, Munger JW, Schroeder W, Soares-Filho BS, Souza CM, Wofsy SC (2012) The Amazon basin in transition. Nature 481(7381):321–328. doi:10.1038/nature10717
Dee DP, Uppala SM, Simmons AJ, Berrisford P, Poli P, Kobayashi S, Andrae U, Balmaseda MA, Balsamo G, Bauer P, Bechtold P, Beljaars ACM, van de Berg L, Bidlot J, Bormann N, Delsol C, Dragani R, Fuentes M, Geer AJ, Haimberger L, Healy SB, Hersbach H, Hólm EV, Isaksen L, Kållberg P, Köhler M, Matricardi M, McNally AP, Monge-Sanz BM, Morcrette JJ, Park BK, Peubey C, de Rosnay P, Tavolato C, Thépaut JN, Vitart F (2011) The ERA-interim reanalysis: configuration and performance of the data assimilation system. Q J Roy Meteor Soc 137(656):553–597. doi:10.1002/qj.828
Deser C, Phillips A, Bourdette V, Teng H (2010) Uncertainty in climate change projections: the role of internal variability. Clim Dyn 38(3–4):527–546. doi:10.1007/s00382-010-0977-x
Dickinson RE, Oleson KW, Bonan G, Hoffman F, Thornton P, Vertenstein M, Yang Z-L, Zeng X (2006) The community land model and its climate statistics as a component of the community climate system model. J Clim 19(11):2302–2324. doi:10.1175/jcli3742.1
Doi T, Vecchi GA, Rosati AJ, Delworth TL (2012) Biases in the Atlantic ITCZ in seasonal-interannual variations for a coarse and a high resolution coupled climate model. J Clim. doi:10.1175/jcli-d-11-00360.1
Donner LJ, Wyman BL, Hemler RS, Horowitz LW, Ming Y, Zhao M, Golaz J-C, Ginoux P, Lin SJ, Schwarzkopf MD, Austin J, Alaka G, Cooke WF, Delworth TL, Freidenreich SM, Gordon CT, Griffies SM, Held IM, Hurlin WJ, Klein SA, Knutson TR, Langenhorst AR, Lee H-C, Lin Y, Magi BI, Malyshev SL, Milly PCD, Naik V, Nath MJ, Pincus R, Ploshay JJ, Ramaswamy V, Seman CJ, Shevliakova E, Sirutis JJ, Stern WF, Stouffer RJ, Wilson RJ, Winton M, Wittenberg AT, Zeng F (2011) The dynamical core, physical parameterizations, and basic simulation characteristics of the atmospheric component AM3 of the GFDL global coupled model CM3. J Clim 24(13):3484–3519. doi:10.1175/2011jcli3955.1
Dunne JP, John JG, Adcroft AJ, Griffies SM, Hallberg RW, Shevliakova E, Stouffer RJ, Cooke W, Dunne KA, Harrison MJ, Krasting JP, Malyshev SL, Milly PCD, Phillipps PJ, Sentman LA, Samuels BL, Spelman MJ, Winton M, Wittenberg AT, Zadeh N (2012) GFDL’s ESM2 global coupled climate-carbon earth system models. part I: physical formulation and baseline simulation characteristics. J Clim 25:6646–6665. doi:10.1175/jcli-d-11-00560.1
Endfield DB, Mestas-Nunez AM, Trimble PJ (2001) The Atlantic multidecadal oscillation and its relation to rainfall and river flows in the continental U.S. Geophys Res Lett 28(10):2077–2080
Field CB, Behrenfeld MJ, Randerson JT, Falkowski P (1998) Primary production of the biosphere: integrating terrestrial and oceanic components. Science 281(5374):237–240. doi:10.1126/science.281.5374.237
Flato GM (2011) Earth system models: an overview. WIREs Clim Change 2(6):783–800. doi:10.1002/wcc.148
Friedlingstein P, Cox P, Betts R, Bopp L, von Bloh W, Brovkin V, Cadule P, Doney S, Eby M, Fung I, Bala G, John J, Jones C, Joos F, Kato T, Kawamiya M, Knorr W, Lindsay K, Matthews HD, Raddatz T, Rayner P, Reick C, Roeckner E, Schnitzler KG, Schnur R, Strassmann K, Weaver AJ, Yoshikawa C, Zeng N (2006) Climate-carbon cycle feedback analysis: results from the C4MIP model intercomparison. J Clim 19(14):3337–3353. doi:10.1175/jcli3800.1
Fu R, Li W (2004) The influence of the land surface on the transition from dry to wet season in Amazonia. Theor Appl Climatol 78:97–110. doi:10.1007/s00704-004-0046-7
Fu R, Zhu B, Dickinson RE (1999) How do atmosphere and land surface influence seasonal changes of convection in the tropical Amazon? J Clim 12:1306–1321
Garreaud RD, Wallace JM (1998) Summertime incursions of midlatitude air into subtropical and tropical South America. Mon Weather Rev 126:2713–2733
Gent PR, Danabasoglu G, Donner LJ, Holland MM, Hunke EC, Jayne SR, Lawrence DM, Neale RB, Rasch PJ, Vertenstein M, Worley PH, Yang Z-L, Zhang M (2011) The community climate system model version 4. J Clim 24(19):4973–4991. doi:10.1175/2011jcli4083.1
Giannini A, Saravanan R, Chang P (2004) The preconditioning role of tropical Atlantic variability in the development of the ENSO teleconnection: implications for the prediction of Nordeste rainfall. Clim Dyn 22(8):839–855. doi:10.1007/s00382-004-0420-2
Gleckler PJ, Taylor KE, Doutriaux C (2008) Performance metrics for climate models. J Geophys Res 113(D6). doi:10.1029/2007jd008972
IPCC (2007) Climate change 2007: the physical science basis. In: Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) Contribution of working group I to the fourth assessment report of the intergovermental panel on climate change
Jones CD, Hughes JK, Bellouin N, Hardiman SC, Jones GS, Knight J, Liddicoat S, O’Connor FM, Andres RJ, Bell C, Boo KO, Bozzo A, Butchart N, Cadule P, Corbin KD, Doutriaux-Boucher M, Friedlingstein P, Gornall J, Gray L, Halloran PR, Hurtt G, Ingram WJ, Lamarque JF, Law RM, Meinshausen M, Osprey S, Palin EJ, Parsons Chini L, Raddatz T, Sanderson MG, Sellar AA, Schurer A, Valdes P, Wood N, Woodward S, Yoshioka M, Zerroukat M (2011) The HadGEM2-ES implementation of CMIP5 centennial simulations. Geosci Model Dev 4(3):543–570. doi:10.5194/gmd-4-543-2011
Lee J-E, Lintner BR, Boyce CK, Lawrence PJ (2011) Land use change exacerbates tropical South American drought by sea surface temperature variability. Geophys Res Lett 38(19). doi:10.1029/2011gl049066
Li W, Fu R (2004) Transition of the large-scale atmospheric and land surface conditions from the dry to the wet season over amazonia as diagnosed by the ECMWF re-analysis. J Clim 17:2637–2651
Li W, Fu R, Dickinson RE (2006) Rainfall and its seasonality over the Amazon in the 21st century as assessed by the coupled models for the IPCC AR4. J Geophys Res 111(D2). doi:10.1029/2005jd006355
Liebmann B, Marengo JA (2001) Interannual variability of the rainy season and rainfall in the Brazilian Amazon basin. J Clim 14:4308–4318
Lorenz C, Kunstmann H (2012) The hydrological cycle in three state-of-the-art reanalyses: intercomparison and performance analysis. J Hydrometeorol. doi:10.1175/jhm-d-11-088.1
Malhi Y, Wright J (2004) Spatial patterns and recent trends in the climate of tropical rainforest regions. Philos Trans R Soc Lond B Biol Sci 359(1443):311–329. doi:10.1098/rstb.2003.1433
Marengo JA (2005) Characteristics and spatio-temporal variability of the Amazon River basin water budget. Clim Dyn 24(1):11–22. doi:10.1007/s00382-004-0461-6
Marengo JA, Liebmann B, Kousky VE, Filizola NP, Wainer IC (2001) Onset and end of the rainy season in the Brazilian Amazon Basin. J Clim 14:833–852
Marengo JA, Tomasella J, Alves LM, Soares WR, Rodriguez DA (2011) The drought of 2010 in the context of historical droughts in the Amazon region. Geophys Res Lett 38(12). doi:10.1029/2011gl047436
Marsland SJ, Haak H, Jungclaus JH, Latif M, Röske F (2003) The Max-Planck-Institute global ocean/sea ice model with orthogonal curvilinear coordinates. Ocean Model 5(2):91–127. doi:10.1016/s1463-5003(02)00015-x
Marti O, Braconnot P, Dufresne JL, Bellier J, Benshila R, Bony S, Brockmann P, Cadule P, Caubel A, Codron F, de Noblet N, Denvil S, Fairhead L, Fichefet T, Foujols MA, Friedlingstein P, Goosse H, Grandpeix JY, Guilyardi E, Hourdin F, Idelkadi A, Kageyama M, Krinner G, Lévy C, Madec G, Mignot J, Musat I, Swingedouw D, Talandier C (2010) Key features of the IPSL ocean atmosphere model and its sensitivity to atmospheric resolution. Clim Dyn 34(1):1–26. doi:10.1007/s00382-009-0640-6
Martin GM, Bellouin N, Collins WJ, Culverwell ID, Halloran PR, Hardiman SC, Hinton TJ, Jones CD, McDonald RE, McLaren AJ, O’Connor FM, Roberts MJ, Rodriguez JM, Woodward S, Best MJ, Brooks ME, Brown AR, Butchart N, Dearden C, Derbyshire SH, Dharssi I, Doutriaux-Boucher M, Edwards JM, Falloon PD, Gedney N, Gray LJ, Hewitt HT, Hobson M, Huddleston MR, Hughes J, Ineson S, Ingram WJ, James PM, Johns TC, Johnson CE, Jones A, Jones CP, Joshi MM, Keen AB, Liddicoat S, Lock AP, Maidens AV, Manners JC, Milton SF, Rae JGL, Ridley JK, Sellar A, Senior CA, Totterdell IJ, Verhoef A, Vidale PL, Wiltshire A (2011) The HadGEM2 family of met office unified model climate configurations. Geosci Model Dev 4(3):723–757. doi:10.5194/gmd-4-723-2011
Medvigy D, Walko RL, Avissar R (2012) Simulated links between deforestation and extreme cold events in South America. J Clim 25(11):3851–3866. doi:10.1175/jcli-d-11-00259.1
Moura AD, Shukla J (1981) On the dynamics of droughts in Northeast Brazil: observations, theory and numerical experiments with a general circulation model. J Atmos Sci 38(12):2653–2675. doi:10.1175/1520-0469(1981)038<2653:otdodi>2.0.co;2
Negrón Juárez RI, Li W, Fu R, Fernandes K, de Oliveira Cardoso A (2009) Comparison of precipitation datasets over the tropical South American and African continents. J Hydrometeorol 10(1):289–299. doi:10.1175/2008jhm1023.1
Nepstad DC, Verssimo A, Alencar A, Nobre C, Lima E, Lefebvre P, Schlesinger P, Potter C, Moutinho P, Mendoza E, Cochrane M, Brooks V (1999) Large-scale impoverishment of Amazonian forests by logging and fire. Nature 398(6727):505–508
Petersen WA, Fu R, Chen M, Blakeslee R (2006) Intraseasonal forcing of convective and lightning activity in the Southern Amazon as a function of cross-equatorial flow. J Clim 19:3180–3196
Raddatz T, Reick C, Knorr W, Kattge J, Roeckner E, Schnur R, Schnitzler KG, Wetzel P, Jungclaus J (2007) Will the tropical land biosphere dominate the climate–carbon cycle feedback during the twenty-first century? Clim Dyn 29(6):565–574. doi:10.1007/s00382-007-0247-8
Rao VB, Cavalcanti IFA, Hada K (1996) Annual variation of rainfall over Brazil and water vapor characteristics over South America. J Geophys Res 101(D21):26539–26551. doi:10.1029/96jd01936
Schmidt GA, Ruedy R, Hansen JE, Aleinov I, Bell N, Bauer M, Bauer S, Cairns B, Canuto V, Cheng Y, Del Genio A, Faluvegi G, Friend AD, Hall TM, Hu Y, Kelley M, Kiang NY, Koch D, Lacis AA, Lerner J, Lo KK, Miller RL, Nazarenko L, Oinas V, Perlwitz J, Perlwitz J, Rind D, Romanou A, Russell GL, Sato M, Shindell DT, Stone PH, Sun S, Tausnev N, Thresher D, Yao M-S (2006) Present-day atmospheric simulations using GISS ModelE: comparison to in situ, satellite, and reanalysis data. J Clim 19(2):153–192. doi:10.1175/jcli3612.1
Seth A, Rauscher SA, Rojas M, Giannini A, Camargo SJ (2011) Enhanced spring convective barrier for monsoons in a warmer world? Clim Change 104(2):403–414. doi:10.1007/s10584-010-9973-8
Shin D-B, Kim J-H, Park H-J (2011) Agreement between monthly precipitation estimates from TRMM satellite, NCEP reanalysis, and merged gauge-satellite analysis. J Geophys Res 116(D16). doi:10.1029/2010jd015483
Smith TM, Reynolds RW, Peterson TC, Lawrimore J (2008) Improvements to NOAA’s historical merged land–ocean surface temperature analysis (1880–2006). J Clim 21(10):2283–2296. doi:10.1175/2007jcli2100.1
Sun Y, Solomon S, Dai A, Portmann RW (2006) How often does it rain? J Clim 19:916–934
Taylor KE (2001) Summarizing multiple aspects of model performance in a single diagram. J Geophys Res 106(D7):7183–7192. doi:10.1029/2000jd900719
Taylor KE, Stouffer RJ, Meehl GA (2012) An overview of CMIP5 and the experiment design. Bull Am Met Soc 93(4):485–498. doi:10.1175/bams-d-11-00094.1
Toomey M, Roberts DA, Still C, Goulden ML, McFadden JP (2011) Remotely sensed heat anomalies linked with Amazonian forest biomass declines. Geophys Res Lett 38(19). doi:10.1029/2011gl049041
Trenberth KE, Smith L, Qian T, Dai A, Fasullo J (2007) Estimates of the global water budget and its annual cycle using observational and model data. J Hydrometeorol 8(4):758–769. doi:10.1175/jhm600.1
Vera C, Silvestri G (2009) Precipitation interannual variability in South America from the WCRP-CMIP3 multi-model dataset. Clim Dyn 32(7–8):1003–1014. doi:10.1007/s00382-009-0534-7
Vera C, Silvestri G, Liebmann B, González P (2006) Climate change scenarios for seasonal precipitation in South America from IPCC-AR4 models. Geophys Res Lett 33(13). doi:10.1029/2006gl025759
Vera CS, Gonzalez P, Silvestri G (2009) About uncertainties in WCRP/CMIP3 climate simulations over South America. In: Proceedings of the 9th international conference on southern hemisphere meteorology and oceanography, p 10
Volodin E, Dianskii N, Gusev A (2010) Simulating present-day climate with the INMCM4.0 coupled model of the atmospheric and oceanic general circulations. Izvestiya Atmos Ocean Phys 46(4):414–431. doi:10.1134/s000143381004002x
Wang H, Fu R (2002) Cross-equatorial flow and seasonal cycle of precipitation over South America. J Clim 15:1591–1608
Xie P, Janowiak JE, Arkin PA, Adler R, Gruber A, Ferraro R, Huffman GJ, Curtis S (2003) GPCP pentad precipitation analyses: an experimental dataset based on gauge observations and satellite estimates. J Clim 16(13):2197–2214. doi:10.1175/2769.1
Yu J-Y, Kim ST (2010) Identification of central-Pacific and eastern-Pacific types of ENSO in CMIP3 models. Geophys Res Lett 37(15):L15705. doi:10.1029/2010gl044082
Žagar N, Skok G, Tribbia J (2011) Climatology of the ITCZ derived from ERA Interim reanalyses. J Geophys Res 116(D15). doi:10.1029/2011jd015695
Acknowledgments
We would like to thank Drs. Sergey Malyshev and Elena Shevliakova for their great help with navigating the GFDL supercomputer system and with analyzing the model output at an early stage. We also thank other scientists at GFDL for their invaluable suggestions and comments on our work. We acknowledge colleagues in our group for downloading part of the CMIP5 data sets. This work is supported by the National Science Foundation (NSF) AGS-0937400, the NOAA Climate Program Office Modeling, Analysis, Prediction and Projection (MAPP) Program through Grant NA10OAAR4310157 and Jackson School facilities.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
About this article
Cite this article
Yin, L., Fu, R., Shevliakova, E. et al. How well can CMIP5 simulate precipitation and its controlling processes over tropical South America?. Clim Dyn 41, 3127–3143 (2013). https://doi.org/10.1007/s00382-012-1582-y
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-012-1582-y