Abstract
Seasonal extreme daily precipitation is analyzed in the ensemble of NARCAPP regional climate models. Significant variation in these models’ abilities to reproduce observed precipitation extremes over the contiguous United States is found. Model performance metrics are introduced to characterize overall biases, seasonality, spatial extent and the shape of the precipitation distribution. Comparison of the models to gridded observations that include an elevation correction is found to be better than to gridded observations without this correction. A complicated model weighting scheme based on model performance in simulating observations is found to cause significant improvements in ensemble mean skill only if some of the models are poorly performing outliers. The effect of lateral boundary conditions are explored by comparing the integrations driven by reanalysis to those driven by global climate models. Projected mid-century future changes in seasonal precipitation means and extremes are presented and discussions of the sources of uncertainty and the mechanisms causing these changes are presented.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Extreme weather events can impose significant stress on human and natural systems. Instrumental records indicate that the probability of intense precipitation has increased over much of the extratropics (Groisman et al. 2005). Furthermore, widespread changes in the frequency and severity of intense storms are projected over the course of this century due to human changes to the composition of the atmosphere (Solomon et al. 2007; Sun et al. 2007; Gutowski et al. 2008; Boberg et al. 2009; Karl et al. 2009). Confidence in these projections of future extreme precipitation is undermined by current climate models’ inability to reproduce the observed extreme precipitation statistics of the recent past. In the models used in preparation for the 4th Assessment Report of the Intergovernmental Panel on Climate change, part of this inability is due to inadequacies in the models’ formulation of moist physics while another part is simply due to the low horizontal and vertical resolution of the grid used to represent the globe. A recent analysis of a single global atmospheric model concluded that horizontal resolution is a key factor in that model’s ability to simulate observed extreme precipitation over the contiguous United States (Wehner et al. 2010). That study found that at horizontal resolutions coarser than approximately 50 km, simulated extreme precipitation rates were substantially lower than observed. Eight different regional models integrated as part of the North American Regional Climate Change Assessment Program (NARCCAP) are based on grids of approximately 50 km and provide an opportunity in the present study to explore the effect of differences in model formulation on extreme precipitation statistics at high resolution.
Generalized extreme value theory (GEV) has been previously applied in many studies to describe the statistical behavior of the tails of the distribution of daily averaged precipitation rates (Zwiers and Kharin 1998; Kharin and Zwiers 2000; Kharin and Zwiers 2005; Frei et al. 2006; Beniston et al. 2007; Kharin et al. 2007; Fowler et al. 2007; Schliep et al. 2010; Fowler et al. 2010). A typical methodology to arrive at a GEV description of the tails is to first form a distribution of the “block maxima” extracted from all of the values. In the cited studies, the block maxima are generally the annual or seasonal maxima of daily averaged precipitation. Then fitting techniques such as maximum likelihood or L-moments are applied to this secondary distribution. Further details of GEV distributions and return values are shown in the “Appendix”. Wang and Zhang (2008) presented a statistical downscaling approach fitting precipitation GEV distributions using large-scale circulation and humidity as covariates to provide regional information about changes in precipitation extremes from a global climate model. Enabled by the NARCCAP ensemble of regional climate models, this paper presents a dynamical downscaling approach as an alternative.
Errors in return value estimates from these GEV distributions can be strong functions of the relative magnitude of the chosen return period and the length of the parent data set that the distribution is drawn from. In this study, 20 year return values of seasonal maximum daily precipitation rates are the main variable of interest to represent very rare and extreme events. This return period length is chosen both to be comparable to previous studies (i.e. Kharin et al. 2007; Wehner et al. 2010) and also to mitigate uncertainty in the fit of the extreme value distributions. This latter point is discussed in some detail in Sect. 6. Note that in the NARCCAP protocols, a 20 year return period is shorter than the specified integration periods.
Projected changes in mean precipitation exhibit strong seasonality because the mechanisms for change may be different (Karl et al. 2009). The character of observed extreme precipitation in North America will be revealed in this study to be strongly seasonally dependent as are its projected changes. The ability of the NARCCAP regional climate models to reproduce the 20 year return values of seasonal maximum daily precipitation rates is quantified in this study through the use of several error metrics defined later in the text. These error metrics are averaged over the entire contiguous United States and also its eastern and western portions. These regions are chosen based on the availability of high quality gridded daily observed precipitation rates. The error metrics are also applied to the average seasonal maximum precipitation and seasonal total precipitation rates. By studying the average of the seasonal maxima distribution, insight into the models’ ability to reproduce less rare precipitation events is provided. Comparing the error metrics from both the less rare and very rare precipitation rates with those applied to the average total seasonal precipitation provides useful information about the models abilities to reproduce the width and shape at the upper end of the distribution.
The NARCCAP models are described in the Sect. 2 along with the presentation of maps of 20 year return value of the seasonal maximum daily precipitation rates for two sets of gridded observations and individual NARCCAP models. The error metrics are defined and applied to the models in Sect. 3. Multi-model average changes in extreme precipitation are presented and discussed in Sect. 4. A multi-model weighting scheme based on a subset of the error metrics is discussed in Sect. 5. Sources and magnitudes of uncertainty in modeled precipitation statistics are discussed in Sect. 6. Results are summarized in Sect. 7. Finally, an “Appendix” provides details of GEV distribution formulations as used in this study.
2 The NARCCAP regional models and observations
The NARCCAP is a coordinated multi-model numerical experiment (Mearns et al. 2009). Eight different regional climate models are integrated at similar resolutions over identical periods and with a variety of lateral boundary conditions. Regional climate models simulate only a portion of the planet and require lateral boundary information to be fully complete. In the NARCCAP experiments, all models simulate atmospheric and land conditions only. The limited surface areas covered by ocean have specified sea surface temperatures. The lateral boundary information generally includes fluxes of energy, moisture and momentum and must come from some external source. Full details of the experiment are described on the NARCCAP website, http://www.narccap.ucar.edu/.
In the NARCCAP specifications, these lateral boundary conditions are specified in two different ways. In the first set of the experiments, all eight regional models are identically driven over the period 1979–2003 with the same information provided by the reanalysis of the National Center for Environmental Prediction (NCEP-2). A “reanalysis” is constructed from the output data of a highly constrained climate model. In the NCEP-2 reanalysis, the climate model is a global atmospheric model. Output data from the reanalysis model is provided at a regridded horizontal resolution of 2.5° and 17 vertical levels (Kalnay et al. 1996; Kanamitsu et al. 2002). The constraints are provided by a data assimilation technique based on ensemble Kalman filtering method that incorporates available observations. The assimilated data can include satellite, balloon and in situ observations and is both spatially and temporally heterogeneous. Reanalysis data is often used as a proxy for observations when direct observations are not available. However, it is important in such applications to note that it is the output from a model and contains biases specific to that model.
The second set of NARCCAP experiments replaces the NCEP reanalysis boundary conditions with boundary information provided from selected fully coupled global climate models. Unlike the NCEP driven experiments, these boundary conditions are not all the same and come from four different global models. Due to computational limitations, not every regional model is driven by all of the global models. In fact, no regional model is driven by more than two global models, complicating intercomparison of this portion of the NARCCAP experiments. Also, this second set of NARCCAP experiments spans two different time periods. The first period, 1968–1999, permits comparison with the NCEP driven experiments to ascertain the effect of changing the quality of the lateral boundary conditions. It is presumed that the NCEP fluxes, due to the data assimilation constraints, are closer to reality than that coming from the relatively unconstrained global climate models. Later in this study, we will examine this forcing difference on simulated precipitation statistics. The second time period for this set of NARCCAP experiments spans 2038–2070 and permits assessment of mid twenty-first century changes relative to late twentieth century values. The forcing scenario for these future simulations in both the global and regional climate models was chosen to be SRES A2 (Nakićenović and Swart 2000). This scenario is often referred to as “business as usual” and is the highest greenhouse gas concentration scenario at the end of the twenty-first century in the CMIP3 database (www-pcmdi.llnl.gov). However, over much of the 2038–2070 period, the differences in climate model response to the various SRES scenarios are not statistically significant (Solomon et al. 2007).
The eight different regional models differ only slightly in horizontal and vertical resolution. However, they differ greatly in their formulation, especially in the parameterized subgrid scale processes that act as source terms to the equations of motion. Often referred to simply as “physics”, these processes include subgrid scale turbulence, radiative transport, boundary layer effects and moist processes. The last of these is probably most relevant to this study and generally includes parameterized treatments of shallow and deep convective cloud processes as well as larger scale cloud physics. We now very briefly describe and name the individual NARCCAP regional models in alphabetical order by acronym. The interested reader is referred to the paper by Mearns et al. (2009) and the specific model citations for more details about these models. For clarity purposes, model acronyms in upper case refer to regional climate models and model acronyms in lower case refer to global climate models.
The Canadian Regional Climate Model (CRCM) is documented by Music and Caya (2007). This model was forced by both the Coupled Global Climate Model Version 3 (cgcm3) (Flato et al. 2000) developed at the Canadian Centre for Climate Modelling and Analysis and the Community Climate System Model version 3.0 (ccsm) (Collins et al. 2006) developed at the National Center for Atmospheric Research in addition to the NCEP reanalysis.
The Experimental Climate Prediction Center/Regional Spectral Model was developed at the University of California-San Diego and the Scripps Institute of Oceanography as a local version of the NCEP Regional Spectral Model (Juang and Kanamitsu 1994; Juang et al. 1997). Two versions of this regional model were contributed to the NARCCAP project. The first of these (ECPC) was forced by the NCEP reanalysis and was not forced by any global climate model output. A second contribution (ECP2) was forced by both by the NCEP reanalysis and the Geophysical Fluid Dynamics Laboratory’s global climate model named CM2, referred to in the NARCCAP dataset as gfdl (Delworth et al. 2006).
The Hadley Regional Model (HRM3) was developed by the Hadley Center at the UK MetOffice (Jones et al. 2004). It is also sometimes referred to as PRECIS. This model was forced by output from the Hadley Climate Model (hadcm3) (Pope et al. 2000; Collins et al. 2001) in addition to the NCEP reanalysis.
The Penn State/NCAR mesoscale model (MM5I) integrations were performed by the Iowa State University and is documented in Grell et al. (1995). This model was forced by output from the Community Climate System Model version 3.0 (ccsm) in addition to the NCEP reanalysis.
The Regional Climate Model (RCM3) is supported by the Abdus Salam International Centre for Theoretical Physics (Giorgi et al. 1993) and the NARCCAP contribution was made by the University of California-Santa Cruz. This model was forced by output from the Coupled Global Climate Model (cgcm3) and the Geophysical Fluid Dynamics Laboratory’s CM2 (gfdl) in addition to the NCEP reanalysis.
Two versions of the Weather Research Forecasting model were contributed to the NARCCAP project (Skamarock et al. 2005) One of these, referred to as WRFG, was forced by output from the Community Climate System Model version 3.0 (ccsm) and the Coupled Global Climate Model Version 3 (cgcm3) in addition to the NCEP reanalysis. The other, referred to as WRFP, was only forced by the NCEP reanalysis. The principal difference between these two model formulations is described on the NARCCAP website: “Data from the Weather Research and Forecasting model was originally designated WRFP, the P standing for PNNL (Pacific Northwest National Lab), the home of the modeling group running this model. Data from the updated model has been designated WRFG. In the WRFP run, the model used the Kain-Fritsch convective parameterization scheme (Kain 2004). The updated model uses the Grell scheme instead, which improves the reproduction of temperature and precipitation (Grell and Devenyi 2002). The G in WRFG stands for Grell.”
Three of the regional models, CRCM, ECPC and ECP2, were subject to a “spectral nudging” technique, which imposes a degree of restoration in the interior of the region to the external forcing fields provided by the NCEP reanalysis or the global climate models. The remainder of the regional models were unconstrained in the interior of the region.
The output from the highest resolution version of a global atmospheric model used in the earlier study by Wehner et al. (2010), the Community Atmospheric Model (fvCAM2.2) is also analyzed in some figures below. This data spans a slightly different period, 1979–1996, but provides a useful comparison in this study to a high-resolution global model.
Gridded observations of accumulated daily precipitation over the contiguous United States (CONUS) used to calculate mean and extreme precipitation statistics are available from two different high-resolution sources. Both sources used the same raw weather station data but differed in the gridding process. The first of these gridded observations is the “NOAA CPC (Climate Prediction Center) 0.25 × 0.25 Daily US Unified Precipitation” dataset (Higgins et al. 2000). These observations are aggregated from three sources of station rain gauge data gridded to a 0.25° × 0.25° grid. Between 8,000 and 13,000 stations were quality controlled and gridded to about 18,000 grid points using a modified Cressman (1959) scheme. Hence, there are likely many grid points with no stations as well as many with multiple stations. The density of station data is least in the Western mountainous and desert regions. The second source of gridded CONUS daily precipitation, referred to here as the University of Washington (UW) dataset, was constructed by Maurer et al. (2002). These authors used the PRISM technique to add an elevation correction (Daly et al. 1997). This correction is particularly influential in mountainous regions where many of the weather stations are at a lower altitude than the average gridded elevation. This dataset is gridded on a 1/8° mesh. In some seasons and/or regions there are significant differences between the precipitation statistics of these two gridded daily precipitation datasets. These differences give some context to the differences between the regional models and either set of observations.
Calculation of mean and extreme precipitation statistics were performed on each regional model’s native grid. These results were then regridded by the NCAR Command Language (NCL) routine RCM2RGRID (http://www.ncl.ucar.edu) to the 0.5° × 0.625° grid used by fvCAM2.2 for plotting and analysis purposes. This grid is at a resolution of approximately 50 km, hence the data transformations from the regional grids are not too severe. The RCM2RGRID routine uses a simple inverse distance weighting and may not be conservative. This order of operations was chosen to save the computational cost of regridding the models’ entire daily precipitation dataset. Previous work (Wehner et al. 2010) reveals a dependence of extreme precipitation values on grid resolution. Hence, the daily observations were regridded to the coarser 0.5° × 0.625° grid prior to any statistical calculations to provide comparison at similar if not exact horizontal grid resolutions. As the regional model resolutions are of similar scale to the 0.5° × 0.625° mesh, significant biases are not expected.
3 Observed and simulated very extreme precipitation in the recent past
3.1 Observations
Figure 1a shows the 20-year return values of seasonal maximum daily precipitation rates obtained from the NCDC CPC gridded observations. Perhaps the most striking aspect of these four panels is the division between east and west centered near the Mississippi River. Also of interest is the seasonality exhibited by these very rare events. In the southeast US, the smallest values are in the summer (JJA) with values in the other three seasons roughly of the same magnitude. This is despite the fact that in the autumn (SON), extreme precipitation of this severity is likely due to Atlantic hurricane activity whereas the source of winter (DJF) and spring (MAM) extreme precipitation is likely from severe storms moving across the mid-continent. In the upper Midwest US, the situation is reversed with the largest magnitudes occurring in the summer. In much of coastal Western US, little precipitation of any form is realized in the summer and the observed extreme precipitation reflects this with a low value. In this part of the nation, the largest values are in winter and exhibit a dependence on orography. In the mountainous portion of the Western US and the western portion of the Great Plains, extreme precipitation is less than elsewhere, with a minimum in the winter for most areas. It should be noted again that the original station data is sparse in some areas. These features of spatial heterogeneity and seasonality can provide rigorous tests of the models’ ability to reproduce the real world.
Figure 1b shows the 20-year return values of seasonal maximum daily precipitation rates obtained from the UW gridded observed daily precipitation rates. Although the general character of these four seasonal plots is similar to those in Fig. 1a, there are important differences. The mountainous regions of the western United States have dramatically higher values in all seasons and much finer detail in the returns values calculated from Maurer dataset than in those calculated from the NCDC CPC dataset. Conversely, the large return values in the eastern United States are lowered by this change in daily datasets. The seasonality and the large east/west gradient are very similar in these two sets of figures. Differences in the seasonal mean precipitation between the two gridding methods is minimal relative to these differences in extreme precipitation. In general, NARCCAP model performance is judged to be in slightly better agreement with the UW dataset than with the NCDC CPC datasets. The model assessments presented below are confined to comparison with the UW gridded observations in the interests of brevity. However, conclusions about relative model performance are not significantly sensitive to which observations are used.
3.2 The NCEP reanalysis driven NARCCAP ensemble of the recent past
Figure 2a–g show the 20-year return values of seasonal maximum daily precipitation rates obtained for the output of NCEP driven regional models in alphabetical order. The odd shape of the colored portion of the maps show the actual regions simulated by each model and is a result of attempts to construct uniform grids centered over North America. Although similar, each regional model treats this issue in a slightly different manner. Visual inspection of these eight maps reveals the wide variation among the models. Some are uniformly too low as compared to the observed results in Fig. 1, while others are uniformly too high. Large east to west gradients are produced by all of the models, but the extent of the large eastern values varies greatly amongst models. Seasonality in the southeastern US varies widely amongst the models as well, with at least one model simulating the highest values in summer rather than the smallest. Simulation of the western US may fare a bit better in that all models simulate large values in the coastal regions except in the summer, consistent with the observations. Also, the simulations in the mountainous regions and the Great Plains are less than elsewhere with a seasonal minimum in the winter, also consistent with the observations.
No single model stands out as superior to its peers in Fig. 2 by a qualitative visual analysis. The introduction of performance metrics allows quantitative intercomparison between models. The area averaged percent error (E) or bias of a model result with respect to an observed result can be written as
where the sums over i and j are a sum over all grid points, O ij are the observed results, M ij are the modeled results and w ij are weighting factors unique to each grid cell reflecting the differences in cell areas. The weighting factors may be set to zero by a mask function to pick out specific areas of interest.
Figure 3 is a “performance portrait” showing the models’ percentage error in the seasonal mean precipitation, the average seasonal daily maximum precipitation rate and the 20-year return values of seasonal maximum daily precipitation rates in the simulations forced by the NCEP reanalysis. Performance portraits are a method to show a large amount of information by a graphical method (Covey et al. 2004). Results are shown for each of the four seasons and are averaged separately over the eastern and western portions of the contiguous US. The Eastern US is defined as all US land areas east of longitude 260°W. The Western US is defined as all US land areas west of that position. A metric for a single model is represented by a single rectangular box with four triangles within each box representing each of the four seasons as shown in the legend. The eight different models as forced by the NCEP reanalysis are shown as well as the high resolution global atmospheric model (fvcam2.2) and are arranged in columns. The rightmost columns show these same performance metrics comparing both results from the NCEP reanalysis itself and the NCDC CPC gridded observations to the UW gridded observations. Individual performance metrics are arranged in rows. The top two rows show the models’ percent errors in the seasonal 20-year return values averaged over the Eastern and Western US regions. Most of the models are biased high (indicated by the blue colors) in both regions for all seasons with only a few exceptions.
A performance portrait plot showing the models’ percentage error relative to the UW gridded observations in the seasonal mean precipitation, the average seasonal daily maximum precipitation rate and the 20 year return values of seasonal maximum daily precipitation rates in the simulations forced by the NCEP reanalysis. Results are shown for each of the four seasons and are averaged separately over the eastern and western portions of the contiguous US as defined in the text. The seasons are arranged as quadrants in each box as shown in the legend. Units are percent
The middle two rows of Fig. 3 show the models’ percent errors in the average seasonal maxima. The models’ errors in this moderate measure of extreme precipitation also reveal a significant positive bias and are strongly related to their return value errors. In contrast, the model percent errors in seasonal mean precipitation, shown in the bottom two rows of Fig. 3, are not very related to the errors in either measure of seasonal extreme precipitation. A comparison of the sign of the regional models’ mean precipitation errors to the sign of their errors in the two measures of extreme precipitation reveals a 51 % agreement rate. Many of the models are biased very low in the mean precipitation but very high in extreme precipitation. Hence, a model’s performance in simulating extreme precipitation cannot be predicted based on its ability to simulate mean precipitation. On the other hand, 80 % of the signs of the model errors in the average seasonal maximum precipitation rates agree with the signs of the model return value errors.
With the exception of the CRCM model, the regional models’ extreme precipitation rates are slightly closer to the UW data than to the NCDC CPC data. The regional model’s mean precipitation rates do not exhibit a clear preference although the ensemble mean precipitation rate is slightly closer to the NCDC CPC data than the UW data. The most striking features of Fig. 3 are the large errors exhibited by the WRFG model in the extreme precipitation rate. This discrepancy is puzzling as the mean precipitation rate error is relatively low and is not exhibited by WRFG when driven by the GCM boundary conditions as discussed further in Sect. 3c. The ensemble mean exhibits lower than average model error in the mean precipitation but the large WRFG error adversely effects the mean model’s error in extreme precipitation.
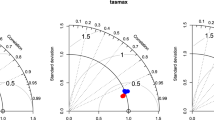
Another method to graphically depict model performance is provided by Taylor diagrams (Taylor 2001). A Taylor diagram is a radial plot where the distance from the origin is a normalized standard deviation of the model output (relative to observations)
and the cosine of the azimuthal angle is given by the centered pattern correlation factor of the model output with the observations (Houghton et al. 2001). In this study, the normalized standard deviation provides a measure of both the models’ spatial hetereogeneity and error. The centered pattern correlation factor, R, removes the bulk error and reveals information about the similarity in pattern between models and observation. A perfect simulation would be plotted at a distance of one from the origin and at an angle of 0°. The distance from a model’s actual point in the Taylor diagram to this point is proportional to the model’s root mean square error. Taylor (2001) originally interpreted skill in his diagrams in two different ways. His more recent provisional skill is defined as (Taylor 2001)
where R is the pattern correlation, \( \hat{\sigma } \) is the normalized standard deviation and α, β are scaling factors set to one in this analysis. The light gray contour lines in Fig. 4 represent this skill.
Taylor diagrams comparing seasonal precipitation statistics from the NCEP driven NARCCAP models compared to the UW gridded observations. The radial distance is the standard deviation across the entire contiguous US normalized by the observations and is a measure of spatial variation. The cosine of the azimuthal angle is given by the centered pattern correlation between models and observations. The black dot at unit distance and 0° from the origin would indicate perfect agreement. The distance to that dot represents a normalized root mean square error. Winter (DJF) is plotted as blue, spring (MAM) as green, summer (JJA) as red and autumn (SON) as brown. Markers indicating specific models are as in the legend. Top left mean precipitation. Bottom left average seasonal daily precipitation maxima. Bottom right 20 year return value of seasonal maximum daily precipitation
Figure 4 shows Taylor diagrams for seasonal mean precipitation (plot a), average seasonal precipitation maxima (plot b) and 20-year return value of seasonal maximum daily precipitation (plot c) averaged over the land areas of the entire contiguous US (CONUS). The eight NARCCAP regional models, the high resolution global model, the NCEP reanalysis and the NCDC CPC observations are each represented by different symbols as in the legend and the different seasons are represented by different colors. Centered correlation factors generally lie between 0.75 and 0.85 for all three precipitation statistics. Spreads in the normalized standard deviation are larger for the extremes than the means resulting in the largest root mean square errors occurring for the 20-year return values. Taylor’s modified skill scores for many of the models exceed 0.8 for the seasonal means but are decreased and more varying for the extremes. Agreement between the two sets of gridded observations is significantly better with seasonal mean skill scores exceeding 0.95. In contrast to the observed seasonal means, the comparisons of the two gridded observational datasets are indistinguishable from the comparisons of the models with the NCDC CPC observations for the extremes. Comparison of the NARCCAP models with the NCDC CPC observations in Taylor diagrams reveals poorer skill scores for all three precipitation statistics stemming mostly from smaller pattern correlation values. Skill scores averaged over seasons are summarized in Table 1.
As with the error metrics shown in Fig. 2, the WRFG model performs poorly on the extremes and is the only model with skill scores less than 0.5. Nonetheless, the ensemble average scores better than any individual NARCCAP model for the seasonal mean and extreme precipitation in Table 1 when judged against either gridded observation set.
As discussed earlier, structural features of the observed mean and extreme precipitation permit construction of very specific performance metrics. The strong east to west gradient is the first of these considered here. The “East/West Index” is defined first by calculating the area weighted averages over the Eastern US, Western US and CONUS regions as defined above. Normalizing the difference of the Western US and Eastern US averages by the CONUS average creates a quantity of interest to compare the models with observations. An index is created by either calculating the difference of the model and observed quantities or by calculating the ratio. In the case of the East/West Index, the difference revealed more interesting structure across models than did the ratio. The following equation summarizes the definition of the East/West Index,
The range of this index can span a wide range. Hence, for this index and for the others to follow, they are normalized in this study. Normalization allows evaluation of models across different performance aspects in a convenient and simple format. The normalization is imposed by determining the worst result across seasons for all sets of East/West indices and assigning it a value of ±100 depending on whether that result is positive or negative. The other results are then normalized with respect to that value. This choice of normalization allows comparison across seasons and between the three variables that are tested. In Fig. 5, the normalized indices relative to the UW gridded observations are presented as a performance portrait in a format similar to Fig. 3. The rows are divided into four groups. The bottom group of six rows presents the same area averaged errors shown in Fig. 3 except normalized for comparison to the other metrics. The second to the bottom group of three rows shows the East/West Index for seasonal mean precipitation, average seasonal precipitation maxima and 20-year return value of seasonal maximum daily precipitation. Negative values (blue in Fig. 5) of the East/West index indicate that the models’ Eastern US climatologies are overactive relative to their Western US climatologies and are most often the case in the winter, spring and fall seasons. In summer, some of the models exhibit the reverse behavior of overactive Western US climatologies. Compared to the averaged error index discussed above, the mean precipitation East/West index is a better predictor of the sign of the extreme precipitation indices with a combined 78 % chance of agreement. Furthermore, there is an 89 % agreement in the signs of the East/West indices when comparing between the two measures of extreme precipitation rates.
Relative errors and performance indices for the regions and seasons shown in Fig. 3 comparing the NCEP forced models with the CPC observations. Units are dimensionless relative to the worst performing model which is assigned a value of ±100
The shape of the distribution of observed daily precipitation rates provides another interesting model performance metric. A simple method of quantifying the relationship of the tail of the distribution to the rest of the distribution is to calculate the differences between combinations of the three precipitation statistics presented in this paper. The difference between the average seasonal maxima and the mean value provides one measure of the width of the parent distribution far down the tail. An even wider measure of the distribution size is provided by the difference of the return values and the means. The difference between the return values and the average seasonal maxima provides a measure of width of the GEV distribution at this point in the tail. The “Tail Index” is defined as
where statistic 1 or 2 are the mean values, the average seasonal maxima or the return values. This index is calculated as a ratio rather than a difference to compress the wider range of values across models than is found for the other indices. Unity is subtracted from the ratio to permit direct comparison to model performance in the other indices. The top six rows of Fig. 5 show the normalized version of the three Tail Indices averaged over the Eastern and Western US regions. Generally, the tail indices measuring the distribution width from the mean value are positive indicating that the tails of the models’ daily precipitation distribution are more distant from the mean than the observations. With only a few exceptions, model performance in replicating the difference of the 20-year return values from the mean values is similar to the model performance in the difference of the average seasonal maxima from the mean value. It also follows that these errors are directly related to errors in the GEV location parameter, ξ, in Eq. 8. 79 % of the errors in the difference between the average seasonal maxima and mean precipitation are positive, indicating that the location parameter is greater in those modeled results than in the NCDC CPC observations. Hence, the distribution of seasonal maximum daily precipitation rates is shifted to greater values (relative to the mean precipitation rate) for the models than for the observations. The difference between the 20-year return values and the average seasonal maxima is determined by the width and shape of the GEV distribution and not its location. Hence, errors in this difference, shown in the top two rows of Fig. 5, reflect errors in the GEV scale parameter, α and shape parameter, k in Eq. 7. For long return periods, the errors in return values (Eq. 10) would be more dependent on errors in the shape parameter than they would be for shorter return times. 81 % of these errors in the regional models are positive indicating a wider GEV distribution in those modeled results than in the observations. None of the negative results for any of the Tail Indices are sizable. Differences between mean and extreme precipitation statistics could be influenced by errors in estimates of mean precipitation due to excessive drizzle. To test this hypothesis, the seasonal mean precipitation was recalculated ignoring daily precipitation values less than 0.1 mm/day. Over the CONUS region used in these performance metrics, the reduction in model estimates of seasonal mean precipitation never exceeds 2 %. Larger reductions were noted in the extreme northern and southwestern portions of the regional domain for all NARCCAP models but do not enter into the calculation of the Tail indices.
Confidence in the above measures of model performance in simulating long period return values would be undermined if the GEV distribution is not a good fit to the sample of seasonal precipitation maxima. The goodness of fit of the GEV distribution to extreme precipitation has been discussed previously by Kharin and Zwiers (2000) and Kharin et al. (2007) by applying a Kolmogorov–Smirnov (KS) test to the transiently forced runs in the CMIP3 database of climate model integrations. They found that the GEV distribution adequately describes annual precipitation extremes for periods of approximately the same duration as considered in this study. They note that only in certain overly dry biased models is the GEV distribution fit poor. To assess the NARCCAP model behavior, an Anderson–Darling (AD) test was applied to the NCEP driven regional model output. This test is limited to the Weibull distribution, the GEV distribution (Eq. 8) with a negative shape parameter, k, but has more power at the tails than the KS test. The test reveals a systematically poor fit in the southwest corner of the NARCCAP domain for every regional model. During the JJA season, some of the models also exhibit a poor fit over dryer regions of the CONUS region. However, in the other three seasons, the fitted distribution adequately describes the distribution of seasonal maxima in the CONUS region implying that the estimates of 20-year return values used in the performance are robust. Note that estimates of average seasonal maxima are unaffected by the goodness of fit.
Figures 3, 4, 5 and Table 1 also contain performance measures of a high resolution (0.5° × 0.625°) global atmospheric model (fvCAM2.2), the NCEP reanalyses themselves and the two sets of observations as compared against each other. The comparisons of the two sets of gridded observations against each other reveal that the effects of elevation corrections are small for seasonal mean precipitation but significant for extreme precipitation as was also evident from a visual comparison of Fig. 1. In all cases, except the NCEP seasonal mean precipitation, agreement between these models and observations is better when the UW dataset is used then when the NCDC CPC dataset is used. Due to the small difference between the seasonal means of the two gridded observations, this effect is larger for the extremes than for the means.
The performance of the global model is essentially indistinguishable from the NARCCAP regional models even though it is not constrained over North America by the reanalysis.
The percent errors in the coarser resolution NCEP reanalysis are lower than any of the individual models (Fig. 3). However, its Taylor skill is in the middle of the range of model skills. Hence, the NARCCAP style of dynamical downscaling does not appear to offer significant benefits in improving skill in simulating mean or extreme precipitation when considering individual models. On the other hand, the NARCCAP ensemble average does exhibit greater Taylor skill than the NCEP reanalysis. However, this unweighted ensemble average is adversely affected by the large errors in the extreme precipitation produced by the WRFG model. Downweighting or even neglecting this particular model in the ensemble average calculations could further improve this downscaled simulation. Section 5 discusses the impact of model weighting on estimating precipitation statistics and their changes in the NARCCAP experiment.
3.3 The GCM driven NARCCAP ensemble of the recent past
Six of the NARCCAP models were driven by output from global climate models (GCM) over the period 1968–1999. Due to computational and fiscal constraints, not every regional model was driven by each gcm. Table 2 summarizes the nine combinations available from the NARCCAP Earth System Grid data portal. Presumably, the GCM representation of the lateral boundary conditions are not as realistic as those provided by the NCEP reanalysis as they are not directly constrained by observations. Hence, it is expected that simulated precipitation statistics from the GCM driven NARCCAP ensemble would be a less accurate representation of the observed precipitation statistics compared to those obtained from the NCEP driven NARCCAP ensemble. Taylor diagrams in Fig. 6 show this change in model performance as measured against the UW gridded observations. In Fig. 6, the NCEP driven RCM result is shown at the tail of an arrow as a unique symbol (as in the legend and Fig. 3). The GCM driven results are shown at the head of these arrows. Some NARCCAP models were driven by two gcms and have two arrows emanating from the tail. The different seasons are represented by the same colors as in Fig. 3. As expected, nearly all of the regional models are degraded by using the GCM output as lateral boundary conditions. Cases with the expected degradation in model skill exhibit a mix of degradations in both correlations and normalized standard deviations. However, all four seasons simulated by the WRFG model and the summer in the RCM3 model exhibit dramatic improvements in the simulation of the average seasonal maximum and return value measures of extreme precipitation. The reason for this improvement in model performance when the lateral boundary conditions are degraded is unclear. Examination of the performance portrait of model errors shown in Fig. 3, and the maps in Fig. 2e, f reveal that the simulated extremes in these seasons are far too large in the NCEP driven versions of these two models. From Fig. 6, these improvements come from a reduction in magnitude of the extreme precipitation rather than from any change in the pattern correlation with observations. Note that both RCM3 and WRFG were driven by two different GCM boundary conditions and each of these simulations performs better than their NCEP driven counterparts in these seasons. Three possible hypotheses as to the source of this error reduction come to mind. First, these particular NCEP driven simulations could be outliers. This possible explanation would be made more credible if the return value but not the average seasonal maximum was improved. If this were the case, a few very intense storms realized by chance over the 24 year NCEP simulation period (1979–2003) could cause the 20-year return value to be larger than would be expected from a longer period. However, this is not the case as the magnitude (and error) of the average seasonal maximum is also reduced in the GCM driven simulations suggesting that the large precipitation events in the NCEP driven simulations are larger than their counterparts in the GCM driven simulations for these two NARCCAP models. Confirmation or rejection of this hypothesis would require multiple realizations of both the NCEP and GCM driven model configurations. Unfortunately, these are not available in the NARCCAP experiment. A second hypothesis of the cause of this improvement is that the simulated extreme precipitation produced by these two models responds to the different lateral boundary conditions in very different ways. Noting that RCM3 and WRFG show improvement in either of the two different GCM driven simulations would suggest that they react adversely to the NCEP lateral boundary conditions. However, the CRCM, ECP2, HRM3 and MM5I models all exhibit better simulation of precipitation extremes when driven by NCEP than when driven by a GCM. This hypothesis gains some credibility by the unusual behavior in the southeast corner of the NARCCAP domains noted in the Sect. 3b. Recall that both ends of the precipitation distribution behave poorly for every model. This effect is worst for RCM3 and WRFG. One might speculate that interactions between the location of the southern boundary and the general circulation could propagate into the entire regional domain. However, multiple realizations with different domain sizes would be required to definitively accept or reject this hypothesis. The third hypothesis is that an error in model formulation or data submission is responsible for this discrepancy. However, this seems unlikely given the care attended to in the NARCCAP experiment.
Taylor diagrams similar to Fig. 4 comparing seasonal precipitation statistics from the NARCCAP models with the UW gridded observations. In this figure, the effect of lateral boundary conditions are shown. Results from the NCEP driven runs are at the tail of the arrows and results from the global model driven runs are at the heads of the arrows. Top left mean precipitation. Bottom left average seasonal daily precipitation maxima. Bottom right 20 year return value of seasonal maximum daily precipitation
Table 2 shows Taylor’s provisional skill value averaged over seasons for the GCM driven NARCCAP simulations of the recent past. Also, the ensemble average of the precipitation extreme and mean values performs significantly better than any individual model when compared to both datasets. Because of the reduction in the WRFG and RCM3 errors, variation in model performance across the GCM driven simulations is much smaller than for the NCEP driven simulations and is likely the reason why the ensemble average performs better in the GCM driven case than in the NCEP driven case relative to the individual models.
4 Projection of future changes in seasonal precipitation statistics
Projections of future climate change based on a single realization of a single climate model are limited in their credible detailed information at the regional scales targeted by the NARCCAP experiments. Especially for extreme event statistics, patterns of climate change in single realizations can be dominated by just a few storms. The real world, of course, is only a single realization, and future climate change will resemble single simulation projections in the sense that it will be realized with significant spatial heterogeneity. However, the exact details of this heterogeneity cannot be reproduced for extreme precipitation events by any single realization because of the natural chaotic behavior of the climate system regardless of model quality. Projections from large ensembles of realizations include many more extreme events than actually occur in the real world over the period of interest. Resulting maps of projected changes in extreme precipitation statistics are less spatially noisy as strong storms are more likely to occur at any given location. Because of these considerations, it is important to consider such ensemble projections at regional or finer scales in a probabilistic rather than in a deterministic sense.
The limited ensemble size of the NARCCAP projections poses significant challenges in quantifying such a probabilistic interpretation. Nonetheless, the high Taylor skill in the ensemble mean extreme precipitation of GCM driven simulations of the recent past shown in Fig. 6 and Table 2 suggests that such a multi-model projection still has merit. Confidence in projections of extreme precipitation changes from the CMIP3 or CMIP5 experiments is limited by the ability of the coarse resolution global models to reproduce storms of sufficient intensity (Kharin et al. 2007; Wehner et al. 2010). For instance, Wang and Zhang (2008) found that at the end of the twenty-first century the change in risk of current 20-year return values of precipitation rate was significantly larger using raw global model output (from cgcm3.1) than was estimated by a statistical downscaling method. This overestimation in the change in risk from direct application of the coarse resolution global model output may be a result of an underestimation in the return value itself. Kharin et al. (2007) state that the modest change in horizontal resolution of the cgcm3.1 from ~375 km to ~280 km produced a 15 % increase in the global average of the 20-year precipitation return value and that another global model experienced a 40 % increase when resolution changed from ~280 to ~110 km. Clearly, the effect of horizontal resolution on simulated extreme precipitation varies greatly between climate models. The NARCCAP regional models’ horizontal resolution of around 50 km is considerably higher than the CMIP global models. Wehner et al. (2010) found very large increases in precipitation return value estimates in the CONUS region in global GCM fvCAM2.2 when resolution was increased from about 200 km to about 50 km and that those larger values agreed much better with the NCDC CPC gridded observations but they did not estimate the effect on changes in those return values. It follows then that the NARCCAP regional models provide somewhat better estimates of severe storm statistics than the CMIP global models and that the changes in their extreme precipitation statistics may be larger. However, given the significant differences in moist physics parameterizations and in the absence of a direct comparison between the CMIP and NARCCAP experiments, no claims of superiority of either experiment are made here.
Figure 7 show the percent changes in the ensemble average of the GCM driven NARCCAP regional model simulations from the recent past (1968–1999) to the future (2038–2070). Each of the nine global model-regional model pairs is treated equally in this unweighted projection. Figure 7a shows the percent change in the seasonal mean precipitation rates. Consistent with the CMIP3 projections (Karl et al. 2009), the northern latitudes exhibit increases while the southern latitudes mostly show decreases. Also consistent with the CMIP3 projections is the character of the seasonal cycle in mean precipitation changes with the largest northern increases in winter and the largest southern decreases in summer. Due to the higher NARCCAP resolution, there is more apparent detail in these maps than in Karl et al. (2009) but some of this is not statistically significant (see Sect. 7 for a description of the hatching scheme). However, in general the regions projected to become drier in the NARCCAP projection are smaller than in the CMIP3 projection. In particular, the latitudes where the NARCCAP projection changes sign are considerably to south of that where the CMIP projection changes sign. On the time scale of these projections, increases in atmospheric water vapor induce a change in radiative forcing and a slowing down of the global atmospheric circulation (Held and Soden 2006). These NARCCAP seasonal mean precipitation projections are consistent with the Held and Soden (2006) conclusion that wet regions would get wetter and that dry regions would get dryer in a warmer world due to these mechanisms. Figure 7b shows the percent change in the average seasonal maximum daily precipitation over the same periods. At the continental scale, there are similarities between these maps and those depicted in Fig. 7a with the greatest increases in northern winter and the largest decreases in the southern summer. However, the magnitudes of these large changes (both positive and negative) are mostly reduced for this measure of extreme precipitation compared to those for mean precipitation. Figure 7c shows the percent change in the 20-year return value of the seasonal maximum daily precipitation over these same periods. The patterns of change in this more extreme measure of precipitation are similar to those in Fig. 7b except that regions of positive change experience larger changes and that regions of negative change experience smaller changes or even become slightly positive. Also, the return value changes are spatially noisier than for the average maxima changes. This may reflect the influence of a relatively few number of very intense storms in this calculation due to the limited number of model integrations.
a Multi-model average percent change in the seasonal mean precipitation from the recent past (1968–1999) to the future (2038–2070). Regions where the signal to noise ratio exceeds unity are hatched. b Multi-model average percent change in the average seasonal maximum daily precipitation from the recent past (1968–1999) to the future (2038–2070). Regions where the signal to noise ratio exceeds unity are hatched. c Multi-model average percent change in the 20-year return value of the seasonal maximum daily precipitation from the recent past (1968–1999) to the future (2038–2070). Regions where the signal to noise ratio exceeds unity are hatched (Units:percent)
Table 3 shows the pattern correlation factor between changes in mean and extreme precipitation over the entire NARCCAP region. The average maxima changes and mean changes are highly correlated ranging from 0.78 to 0.89. Pattern correlation factors between return value changes and mean changes are substantially less, ranging from 0.48 to 0.68. The average maxima changes and return value changes are also highly correlated although not perfectly so with correlation factors ranging from 0.85 to 0.92 over the NARCCAP region. These differences in correlation factors imply that the shape of the precipitation distribution changes in a complicated spatially dependent manner. Two leading mechanisms postulated to explain changes in extreme precipitation in a warmer climate are different from the Held and Soden (2006) explanation of future changes in mean precipitation. The first of these suggests because the maximum water vapor is controlled by the Clausius-Clapeyron relationship, changes in extreme precipitation are then largely determined by increases in temperature (Allan and Soden 2008; Allen and Ingram 2002; Kendon et al. 2010; Pall et al. 2007). A second mechanism for extreme precipitation put forth by O’Gorman and Schneider (2009a, b) is that such events are controlled by convective updrafts which would change in a complicated fashion in a warmer world (Sugiyama et al. 2010). If the Clausius-Clapeyron mechanism solely controlled extreme precipitation changes, there would no regions of decreases in Fig. 7b and c since air temperature only increases in these simulations of the future climate. If convective updrafts were the only mechanism controlling extreme precipitation changes, there would be little change in winter as such storms in North America do not typically involve large convective events. The co-location of substantial summertime decreases in the Southwestern US in all three figures suggests that a third mechanism, the availability of transported water vapor, is also important. However, the influence of this mechanism on extreme precipitation changes may diminish with increased rarity as reflected in the lower correlations between return value and mean changes compared to that between average maxima and mean changes (Table 3). It is likely that all three mechanisms contribute to some extent to changes in extreme precipitation. The relative importance of each mechanism likely depends on location, season and the rarity of the extreme events considered.
5 Model weighting
Weighting of models based on their relative ability to reproduce the observed climate of the recent past is a controversial topic. Given the wide range of model performance, it would seem reasonable that claims of detectible anthropogenic climate change or projections of future climate change would be made more robust if they are based on the most credible models. In practice, this has proven elusive. Motivated by trends in either observed or future trends in climatic variables, it would seem logical to focus on model skill in replicating model performance metrics based on trends themselves. However, this task is complicated by two factors. First, the observed trends in climate models are greatly dependent on the prescribed forcing. While most model simulations of the recent past are forced with the same greenhouse gas changes, they differ widely in their prescriptions of aerosols, ozone, volcanoes and solar intensity. This makes it difficult to separate the effects of differences in total radiative forcing changes from differences in climate model sensitivity. Second, for many fields, such as intense precipitation, the record of available observations are not long enough to establish the significance of any agreement or disagreement between observed and modeled trends because of substantial natural variability. For these reasons, most studies of model weighting have focused on models’ abilities to reproduce observed mean fields. For instance, Santer et al. (2008) examined the effect of up to seventy different temperature and humidity model performance metrics on the detection and attribution of satellite observed trends in atmospheric moisture over the global oceans and found that the inclusion or elimination of poorly performing models did not affect their central conclusion of a human influence. They do note that atmospheric moisture trends are particularly vigorous and that an affect might be found in the detectibility of other fields. Collins et al. (2010) examined fifteen different annual mean fields in both the CMIP3 multi-model ensemble as well as a perturbed physics ensemble of the global model, hadcm3, and found that there are no simple relationships between climate model errors in these fields and projections of future climate change. They conclude that the feedback between climate model errors and sensitivity is a multi-variate process but offer no multi-variate metrics to quantify this relationship due to a low likelihood that understanding would be increased or that their implementation in a weighted projection would be straightforward.
However as discussed in the previous section, in the case of extreme precipitation over the CONUS region (and perhaps mid-latitude land regions in general), there is weak evidence that higher resolution models produce larger changes in extreme precipitation than do lower resolution models and stronger evidence that higher resolution models produce more realistic intense storms. The potential for a relationship between the intensity of simulated extreme precipitation and the magnitude of its future change motivates at least an investigation into the effect of weighting the NARCCAP regional models.
The provisional Taylor skills (Eq. 3 and Tables 1, 2) provide a non-unique basis for a simple model weighting scheme for mean and extreme precipitation. Consider a weighting scheme defined by
where s are the provisional Taylor skills, i indicates a particular model and the sum is over N, the number of different models. If all models had the same skill, each model’s weight, w in the weighted ensemble average would be one. However, the models have different skills and two particular models (WRFG and RCM3) in the NCEP driven experiment perform much worse than their peers in their simulation of extreme precipitation (see Table 1). Both of these models simulate extreme precipitation to be significantly more intense than observed. Although not shown in this table, there is a strong seasonal dependence to these two models’ extreme precipitation skill with the summer season being the worst, followed by the fall season. Hence, the following discussion is based on model weights calculated from Eq. 6 on a seasonal basis based on their skill in reproducing the UW observed precipitation statistics. The average of these seasonal weights is shown in Table 4 for the individual NARRCAP models in the NCEP driven ensemble. For the WRFG NCEP driven simulation, the seasonal weights for the 20-year return value are DJF:0.73, MAM:0.61, JJA:0.38 and SON:0.47. For the RCM3 (which has an incorrect extreme precipitation season cycle in the southeast, see Fig. 2e), the seasonal weights are DJF:1.05, MAM:1.01, JJA:0.50 and SON:1.02. Since the lowest model weights are in the JJA season, the highest model weights are also in that season. However, since the JJA weights greater than one are spread out amongst the other six models, the highest value is only 1.30. The range of NARCCAP model weights in the other three seasons (except for WRFG) spans the range 0.95–1.11. The rather severe discounting of WRFG in all seasons and RCM3 in summer causes the weighted ensemble average to be more skillful than the equally weighted ensemble average as shown in Table 6. However, significant improvements in the 20-year return value skill and average seasonal maximum skill are confined to the summer season. Also, there is no significant improvement to the seasonal mean skill in any season as the range of individual model skills is tighter. Simply not including RCM3 and WRFG in an otherwise unweighted average produces essentially the same ensemble mean skill as the more complicated weighting scheme except for the JJA return value which is slightly degraded from the weighted average.
The range of NARCCAP model weighting factors for the GCM driven experiment (Table 5) is much less than it is for the NCEP driven experiment (Table 4). Hence, the effect of weighting on ensemble mean skill is much reduced. To summarize, the effects of using complicated weighting factors are small and difficult to justify over simply rejecting very poorly performing models. In the case of the NARCCAP projections, weighting individual models does little to increase confidence (Table 6).
6 Uncertainty quantification
Identification and quantification of uncertainty in climate model output is critical to understanding how much confidence can be placed in projections of future climate change. Hawkins and Sutton (2009) and Hawkins et al. (2011) discussed the time-evolving significance of three sources of uncertainty: imperfect initial conditions, structural model uncertainty and uncertainty about the human-induced alterations to forcings important to the climate system. The three types of uncertainty identified in the Hawkins et al. studies are, of course, not the only sources of uncertainty nor is the need for uncertainty quantification limited to projections.
For the NARCCAP ensemble, an estimate of the structural uncertainty can be made from the nine combinations of regional and global models, although the entire range of uncertainty is clearly not sampled (Masson and Knutti 2011). The other two uncertainty sources cannot be investigated in the NARCCAP ensemble due to limitations in the experimental design.
Uncertainty in the estimation of long period return values is also sensitive to the size of the parent data set in relation to the length of the period. This source of uncertainty is a reflection of the relative goodness of fit as well as how fully the tail of the extreme value distribution is sampled. Such sample size uncertainty is also relevant to the estimation of lower order statistics but to a lesser degree. As a data record lengthens, the sample size uncertainty decreases because confidence in the estimation of the GEV distribution parameters increases. A bootstrapping method to investigate the effect of sample size on return value estimation uncertainty was put forth by Hosking and Wallis (1997) and has been applied to climate model output in several studies (Kharin and Zwiers 2000, 2005; Wehner 2010). In this method, GEV parameters are first estimated from the actual available sample data. Then, a set of random samples distributed according to this GEV distribution is generated. GEV parameters and associated return values are then calculated for each of these random samples (of the same size as the actual sample). Standard measures of uncertainty, such as variance, can be calculated from these randomized extreme value statistics. This bootstrapping method provides an augmentation to the traditional goodness of fit analysis discussed in Sect. 3b by providing practical statements about the uncertainty of derived extreme value statistics.
This source of uncertainty was analyzed for each of the GCM driven NARCAPP models by generating fifty random samples at all of the models’ original grid points for both the past and future integrations. At the grid point scale, the ratio of the standard deviation across these random samples to the calculated 20-year return values averages about 4 % and generally is less than 10 %. Maps of this ratio for single model integrations are spatially noisy with no particular structures exhibited in any regions or seasons. For the skill values obtained from the Taylor diagrams, this source of uncertainty is negligible (skill varies much less than 1 %) over the entire CONUS region. These low values indicate that the NARCCAP integration periods (~30 years) are long enough to satisfactorily estimate the GEV parameters and obtain a good estimate of the 20-year return values for a particular individual simulation. Estimates of substantially longer period return values from datasets of this size would not be as accurate. Note, this bootstrapping method does not provide any information about how return values would vary from different realizations of the same NARCCAP model, as this is a property of model internal variability rather than a sample size issue.
To estimate the magnitude of this source of uncertainty in multi-model projections of future climate change, consider that the variance of a sum of random variables is the sum of the covariances of those random variables. Then the sample size variance, \( \sigma_{s}^{2} , \) of the unweighted multi-model difference, \( \mathop \Updelta \limits^{\_} , \) of the future state, F, and the past state, P, is:
and is simply the sum of covariances over all combinations of model past and future values. Here, N is the total number of models (which is nine for the GCM driven NARCCAP experiment). It is useful to aid intuition about this formula to consider two limiting cases. If all of the model past and future states are independent of each other and have equal variance \( \sigma_{s}^{2} , \) then \( \sigma_{s}^{2} (\mathop \Updelta \limits^{\_} ) \to 2\sigma_{s}^{2} /N \). If in the opposite limit that all of the model past and future states are completely correlated with each other and have equal variance \( \sigma_{s}^{2} , \) then \( \sigma_{s}^{2} (\mathop \Updelta \limits^{\_} ) \to 0. \)
Hence, the correlation between models is key to determining the magnitude of some of the sources of uncertainty in projections. Equation 7 would also permit the estimation of multi-model projection uncertainty from internal variability if multiple realizations of each model were available. Unfortunately they are not for the NARCCAP ensemble. However, this equation permits estimation of the sample size uncertainty in projections from the random return value generation procedure discussed above by calculating the covariances across the random dimension. Not unexpectedly, comparison of this multi-model sample size projection uncertainty with that from the individual models reveals a low degree of correlation between the randomly generated return values and that this source of uncertainty is reduced by adding more models.
The model formulation uncertainty could be calculated in a similar manner from the sum of covariances as \( \sigma_{M}^{2} (\mathop \Updelta \limits^{\_} ) = \sigma_{M}^{2} (\mathop F\limits^{\_} ) + \sigma_{M}^{2} (\mathop P\limits^{\_} ) - 2\text{cov} (\mathop F\limits^{\_} ,\mathop P\limits^{\_} ), \) where in this case the variances and covariance are calculated across models. Unlike in the sample size uncertainty estimation, the individual models’ past and future states are highly correlated with each other causing a significant reduction to the model formulation uncertainty from the covariance term. Again, in the limit of identical past and future variances and perfect correlation between the two, \( \sigma_{M}^{2} (\mathop \Updelta \limits^{\_} ) \to 0. \) Such a complete formulation of the projection uncertainty clearly reveals the intuitive result that this source of uncertainty is smaller for short-term projections, when the past and future are relatively highly correlated than it is for long-term projections when they are not. However for this source of uncertainty, it is simpler to calculate \( \sigma_{M}^{2} (\mathop \Updelta \limits^{\_} ) \) directly from the individual model projections of change and obtain the same result as Eq. 7. For the NARCCAP projections of changes in 20 year return values, the sample size uncertainty (expressed as a standard deviation) is about 10–20 % of the model formulation uncertainty over much of the land covered regions and should not be ignored when considering the statistical significance of projected changes. For the seasonal mean and average maximum precipitation rates, this source of uncertainty can be safely ignored for the NARCCAP ensemble. Assuming, as in Hawkins and Sutton (2009), that these two sources of uncertainty are independent, the total variance is simply the sum of the variances. The ratio of the multi-model average change to the square root of this total variance provides a convenient signal to noise (S/N) ratio at a 66 % statistical confidence level. Using the IPCC definition of “likely” (Solomon et al. 2007), any region where this S/N ratio is greater than one will likely experience a change of the same sign as the multi-model average change. Projections in areas where this is not the case have a confidence interval that spans zero. The regions where change is “likely” are hatched in Fig. 7. For the seasonal mean precipitation and average seasonal maximum daily precipitation changes, only the model formulation uncertainty is used on the S/N calculation. In general, projections in the more northern portions of the NARCCAP region are the most statistically significant, especially in the winter. Clausius-Clapeyron scaling is the most plausible mechanism for these robust changes. The nonlinear dependence of saturation humidity with temperature results in larger percent increases in the water holding capacity of the atmosphere per degree warming in colder regions than in warmer regions. This property together with larger temperature increases in the high latitudes than in the lower latitudes contribute to the robustness of the changes in mean and extreme precipitation in the northern regions. The profound drying of the seasonal mean precipitation in the southwest US in the spring and summer (and the northwest US summer) is also judged “likely” by this S/N criterion. The S/N ratio is larger for the 2038–2070 NARCCAP seasonal mean projection than it is for the 2080–2099 CMIP3 projection reported in the 2nd US National Assessment Report (Karl et al. 2009), especially for the summertime drying. It is difficult to ascertain whether that is a result of the higher resolution in the NARCCAP models or if the limited number of models inadequately samples the full uncertainty (Knutti et al. 2011). It is important to recall that only four different global models were used to drive the NARCCAP models and that the full range of CMIP3 model circulation changes in North America may not be realized. Also, as Hawkins and Sutton (2010) point out, the relative magnitudes of the projection and its uncertainties are a function of time. Hence, it is possible that there would be less confidence in later projections of seasonal mean precipitation changes with the NARCCAP models, if such were available.
The reduction of the seasonal maximum is very nearly in the “likely” category as well. However, such patterns of high confidence in the return value changes are much less spatially coherent than for the seasonal mean and maxima with no region of decrease achieving a “likely” judgment. Calculation of a 90 % confidence level (where S/N > 1.645) reveals that only very limited high latitude regions of wintertime mean precipitation increases are “very likely” in the IPCC parlance and that no changes in either measure of extreme precipitation can be determined to be “very likely” from the NARCCAP ensemble.
7 Conclusion
Precipitation statistics are analyzed from the NARCCAP regional modeling experiment. The higher resolution of these regional models offers promise towards more realistic simulation of extreme precipitation. Mean values, the average maxima daily precipitation and the 20-year return value of daily precipitation are compared to observations of the late twentieth century and projected into the future on a seasonal basis. Comparison with two sets of daily gridded precipitation obtained from the same raw CONUS station data reveals that the NARCCAP models perform significantly better in the simulation of extreme precipitation when judged against the higher resolution observations containing the PRISM elevation corrections. However despite similar horizontal resolutions, model performance is varied with large variations in their ability to simulate the extreme precipitation statistics. Furthermore, the NARCCAP models’ skill in simulating seasonal mean precipitation is a poor predictor of skill in seasonal extreme precipitation.
In addition to quantification of the models’ average biases in these precipitation statistics, metrics quantifying the contrast between the eastern and western halves of the contiguous US and the relationship between the tails and the mean of the distribution of daily precipitation are applied to the NCEP driven ensemble of NARCCAP simulations. The metrics related to the shape of the precipitation distribution reveal that most of the NARCCAP model distributions are wider at the tails than the observations. For some of these extreme metrics, the unweighted ensemble mean of the NCEP driven models is adversely affected by the RCM3 and WRFG outliers causing it to not be superior to every individual model.
Model performance is also illustrated via Taylor diagrams relating the correlation to observations and a weighted areal standard deviation. Skill values from these diagrams provide an opportunity to develop a model weighting scheme to calculate ensemble average precipitation statistics. For the NCEP driven ensemble, with the WRFG outliers in its extreme precipitation statistics, significant differences in model weighting factors are produced. These generate significant improvements in extreme precipitation skill for the weighted ensemble average than for the unweighted ensemble average. However, for the GCM driven ensemble, there is very little variation in weighting factors and ensemble average skill is not improved by their application. This result encourages the usage of the GCM driven ensemble without weighting for future projection purposes. It is difficult to justify any model weighting scheme more sophisticated than simply rejecting outlying poor performers.
The NARCCAP GCM driven ensemble produces robust changes in future mean precipitation qualitatively similar to the global CMIP3 models (Karl et al. 2009). Statistically significant increases are projected for most of the upper US and Canada in the winter and in most of Canada for the other three seasons. Statistically significant mean precipitation decreases in the western US during the summer and in the southwest US in the spring are also projected. Projections of future changes in the seasonal maxima precipitation and their 20-year return values follow the same general spatial pattern although are less statistically significant. Correlations between seasonal mean and extreme precipitation changes decrease as rarity increases, suggesting that a mixture of physical mechanisms is responsible. In the northern latitudes, increases in the water vapor holding capacity of the warmer atmosphere are likely responsible for both changes in mean and extreme precipitation. The western and southwestern US regions exhibiting statistically significant decreases in seasonal mean precipitation also exhibit decreases in extreme precipitation. It is suggested that these decreases in extreme precipitation are determined by a reduction in water vapor availability caused by the same circulation changes that lead to decreases in seasonal mean precipitation. Extreme precipitation changes thus are controlled by a complex interplay between circulation changes, local temperature changes and convective updraft changes. The relative mix of these mechanisms is a strong function of season, location and rarity of the extreme event. As previously pointed out by Wang and Zhang (2008), projected changes in the GEV parameters can reflect these mechanisms. Circulation changes primarily affect the location parameter, ξ, and hence have little impact on the spread of extreme values, while moisture increases have a strong impact on all the parameters including the scale and shape parameters, α and k, causing a shift in the far tail of the distribution to larger values. An investigation into the sources of projection uncertainty reveals that the uncertainty in 20-year return value changes due to limited sample sizes is smaller than but not negligible to the uncertainty arising due to differences in model formulation.
Confidence in these projections of future changes in precipitation statistics is undermined by the limitations of the NARCCAP ensemble of regional models. For instance, the small number of global models used to provide the lateral boundary conditions fails to fully sample the range of uncertainty to changes in the Hadley Circulation. Hence, the high statistical significance of the projected widespread US summertime drying should not lead to an interpretation that this result is robust. Furthermore, the skill in replicating observed mean and extreme precipitation statistics is not improved in the reanalysis driven experiments over the reanalysis itself. Rather the regional models developed their own errors resulting in significantly different precipitation climatologies challenging the notion that their output is a dynamically downscaled version of their input. Finally, unexplained differences between certain portions of the reanalysis and model driven experiments lead to conflicting interpretations of the NARCCAP models’ true predictive skill.
References
Allan R, Soden B (2008) Atmospheric warming and the amplification of precipitation extremes. Science 321:1481–1484
Allen M, Ingram W (2002) Constraints on future changes in climate and the hydrologic cycle. Nature 419:224–232
Beniston M, Stephenson DB, Christensen OB, Ferro CAT, Frei C, Goyette S, Halsnaes K, Holt T, Jylhä K, Koffi B, Palutikof J, Schöll R, Semmler T, Woth K (2007) Future extreme events in European climate: an exploration of regional climate model projections. Clim Change 81:71–95. doi:10.1007/s10584-006-9226-z
Boberg F, Berg P, Thejll P, Gutowski WJ, Christensen JH (2009) Improved confidence in climate change projections of precipitation evaluating using daily statistics from PRUDENCE ensemble. Clim Dyn 32:1097–1106
Castillo E, Hadi AS, Balakrishnan N, Sarabia JM (2004) Extreme value and related models with applications in engineering and sci ence. Wiley, New York
Coles S (2001) An introduction to statistical modeling of extreme values. Springer, London
Collins M, Tett SFB, Cooper C (2001) The internal climate variability of HadCM3, a version of the Hadley Centre coupled model without flux adjustments. Clim Dyn 17:61–81. doi:10.1007/s003820000094
Collins WD, Bitz CM, Blackmon ML, Bonan GB, Bretherton CS, Carton JA, Chang P, Doney SC, Hack JJ, Henderson TB, Kiehl JT, Large WG, McKenna DS, Santer BD, Smith RD (2006) The community climate system model Version 3 (CCSM3). J Clim 19:2122–2143
Covey C, AcutaRao KM, Gleckler PJ, Phillips TJ, Taylor KE, Wehner MF (2004) Coupled ocean-atmosphere climate simulations compared with simulations using prescribed sea surface temperature: effect of a “perfect ocean”. Glob Planet Change 41:1–14
Daly C, Taylor G, Gibson W (1997) The PRISM approach to mapping precipitation and temperature. In: 10th conference on applied climatology, Reno, NV, Am Meteor Soc, pp 10–12
Delworth T et al (2006) GFDL’s CM2 global coupled climate models—Part 1: formulation and simulation characteristics. J Clim 19:643–674. doi:10.1175/JCLI3629.1
Flato GM, Boer GJ, Lee WG, McFarlane NA, Ramsden D, Reader MC, Weaver AJ (2000) The Canadian centre for climate modeling and analysis global coupled model and its climate. Clim Dyn 16:451–467. doi:10.1007/s003820050339
Fowler HJ, Ekstroem M, Blenkinsop S, Smith AP (2007) Estimating change in extreme European precipitation using a multimodel ensemble. J Geophys Res 112:D18104. doi:10.1029/2007JD008619
Fowler HJ, Cooley D, Sain SR, Thurston M (2010) Detecting change in UK extreme precipitation using results from the climateprediction.net BBC climate change experiment. Extremes 13:241–267
Frei C, Schöll R, Fukutome S, Schmidli J, Vidale PL (2006) Future change of precipitation extremes in Europe: intercomparison of scenarios from regional climate models. J Geophys Res 111:D06105. doi:10.1029/2005JD005965
Giorgi F, Marinucci MR, Bates GT (1993) Development of a second generation regional climate model (RegCM2) I: boundary layer and radiative transfer processes. Mon Weather Rev 121:2794–2813
Grell GA, Devenyi D (2002) A generalized approach to parameterizing convection combining ensemble and data assimilation techniques. Geophys Res Lett 29:1693–1697
Grell G, Dudhia J, Stauffer D (1995) A description of the Fifth-Generation Penn State/NCAR Mesoscale Model (MM5) NCAR Technical Note, NCAR/TN-398 + STR
Groisman PYa, Knight RW, Easterling DR, Karl TR, Hegerl GC (2005) Trends in intense precipitation in the climate record. J Clim 18:1326–1350
Gutowski WJ, Hegerl GC, Holland GJ, Knutson TR, Mearns LO, Stouffer RJ, Webster PJ, Wehner MF, Zwiers FW (2008) Causes of observed changes in extremes and projections of future changes in weather and climate extremes in a changing climate. In: Karl TR, Meehl GA, Miller CD, Hassol SJ, Waple AM, Murray WL (eds), Regions of focus: North America, Hawaii, Caribbean, and U.S. Pacific Islands. A Report by the U.S. Climate Change Science Program and the Subcommittee on Global Change Research, Washington, DC
Held I, Soden B (2006) Robust responses of the hydrological cycle to global warming. J Clim 19:5686–5699
Higgins RW, Shi W, Yarosh E, Joyce R (2000) Improved US Precipitation Quality Control System and Analysis. NCEP/Climate Prediction Center ATLAS No. 7, National Centers for Environmental Prediction, Climate Prediction Center, Camp Springs, Maryland, available at http://www.cpc.ncep.noaa.gov/research_papers/ncep_cpc_atlas/7/index.html. Data is available at http://www.cdc.noaa.gov/cdc/data.unified.html
Hosking JRM, Wallis JR (1997) Regional frequency analysis. An approach based on L-moments. Cambridge University Press, Cambridge
Houghton, JT, Ding Y, Griggs DJ, Noguer M, van der Linden PJ, Dai X, Maskell K, Johnson CA (eds) (2001) Climate change 2001: The Scientific Basis. Contribution of Working Group I to the Third Assessment Report of the Intergovernmental Panel on Climate Change Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, p 881. See Appendix 12.3 for a discussion of pattern correlation
Jones R, Noguer M, Hassell D, Hudson D, Wilson S, Jenkins G, Mitchell J (2004) Generating high resolution climate change scenarios using PRECIS. Met Office Hadley Centre, Exeter, p 40
Juang H-M, Kanamitsu M (1994) The NMC nested regional spectral model. Mon Weather Rev 122:3–26
Juang H-M, Hong SY, Kanamitsu M (1997) The NCEP regional spectral model: an update Bull. Am Meteor Soc 78:2125–2143
Kain JS (2004) The Kain-Fritsch convective parameterization: an update.”. J Appl Meteor 43:170–181
Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, Gandin L, Iredell M, Saha S, White G, Woollen J, Zhu Y, Chelliah M, Ebisuzaki W, Higgins W, Janowiak J, Mo KC, Ropelewski C, Wang J, Leetmaa A, Reynolds R, Jenne R, Joseph D (1996) The NMC/NCAR 40-Year reanalysis project. Bull Am Meteor Soc 77:437–471
Kanamitsu M, Ebisuzaki W, Woollen J, Yang S-K, Hnilo JJ, Fiorino M, Potter GL (2002) NCEP-DOE AMIP-II Reanalysis (R-2). Bull Am Meteor Soc 83:1631–1643
Karl TR, Mellilo JM, Peterson TC (eds) (2009) Global climate change impacts in the United States: a state of knowledge report, Cambridge [England], Cambridge University Press (available at www.globalchange.gov)
Kendon E, Rowell D, Jones R (2010) Mechanisms and reliability of future projected changes in daily precipitation. Clim Dyn 35:489–509
Kharin VV, Zwiers FW (2000) Changes in the extremes in an ensemble of transient climate simulation with a coupled atmosphere-ocean GCM. J Clim 13:3760–3788
Kharin VV, Zwiers FW (2005) Estimating extremes in transient climate change simulations. J Clim 18:1156–1173
Kharin VV, Zwiers FW, Zhang X, Hegerl GC (2007) Changes in temperature and precipitation extremes in the IPCC ensemble of global coupled model simulations. J Clim 20:1419–1444
Masson D, Knutti R (2011) Climate model genealogy. Geophys Res Lett 38:L08703. doi:10.1029/2011GL046864
Maurer EP, Wood AW, Adam JC, Lettenmaier DP, Nijssen B (2002) A long-term hydrologically-based data set of land surface fluxes and states for the Conterminous United States, J Clim 15, 3237–3251 (data available at http://www.engr.scu.edu/~emaurer/data.shtml)
Mearns LO, Gutowski WJ, Jones R, Leung L-Y, McGinnis S, Nunes AMB, Qian Y (2009) A regional climate change assessment program for North America. EOS 90:311–312
Music B, Caya D (2007) Evaluation of the hydrological cycle over the Mississippi River Basin as simulated by the Canadian regional climate model (CRCM). J Hydrometeor 8:969–988
Nakićenović N, Swart R (eds) (2000) Special report on emissions scenarios: a special report of Working Group III on the Intergovernmental Panel on Climate Change. Cambridge University Press, Cambridge
O’Gorman P, Schneider T (2009a) Scaling of precipitation extremes over a wide range of climates simulated with an idealized GCM. J Clim 22:5676–5685
O’Gorman P, Schneider T (2009b) The physical basis for increases in precipitation extremes in simulations of 21st-century climate change. Proc Natl Acad Sci 106:14773–14777
Pall P, Allen M, Stone D (2007) Testing the Clausius-Clapeyron constraint on changes in extreme precipitation under CO2 warming. Clim Dyn 28:351–363. doi:10.1007/s00382-006-0180-2
Pope VD, Gallani ML, Rowntree PR, Stratton RA (2000) The impact of new physical parameterizations in the Hadley Centre climate model—HadAM3. Clim Dyn 16:123–146. doi:10.1007/s003820050009
Schliep E, Cooley D, Sain SR, Hoeting JA (2010) A comparison study of extreme precipitation from six different regional climate models via spatial hierarchical modeling. Extremes 13:219–239
Skamarock WC, Klemp JB, Dudhia J, Gill DO, Barker DM, Wang W, Powers JG (2005) A description of the advanced research WRF Version 2. NCAR Tech Notes-468 + STR (http://www.mmm.ucar.edu/wrf/users/docs/arw_v2.pdf)
Solomon S, Qin D, Manning M, Chen Z, Marquis M, Averyt KB, Tignor M, Miller HL (eds) (2007) Climate Change 2007: The physical science basis. Contribution of working group I to the fourth assessment report of the intergovernmental panel on climate change Cambridge University Press, Cambridge
Sugiyama M, Shiogama H, Emori S (2010) Precipitation extreme changes exceeding moisture content increases in MIROC and IPCC climate models. Proc Natl Acad Sci 107:571–575. doi:10.1073/pnas.0903186107
Sun Y, Solomon S, Dai A, Portmann RW (2007) How often will it rain? J Clim 20:4801–4818
Taylor KE (2001) Summarizing multiple aspects of model performance in single diagram, J Geophys Res 106:7183–7192 (also see http://www-pcmdi.llnl.gov/about/staff/Taylor/CV/Taylor_diagram_primer.htm)
Wang J, Zhang X (2008) Downscaling and projection of winter extreme daily precipitation over North America. J Clim 21:923–937
Wehner MF (2010) Sources of uncertainty in the extreme value statistics of climate data. Extremes 13:205–217. doi:10.1007/s10687-010-0105-7
Wehner MF, Smith R, Duffy P, Bala G (2010) The effect of horizontal resolution on simulation of very extreme US precipitation events in a global atmosphere model. Clim Dyn 32:241–247. doi:10.1007/s00382-009-0656-y
Zwiers FW, Kharin VV (1998) Changes in the extremes of the climate simulated by CCC GCM2 under CO2 doubling. J Clim 11:2200–2222
Acknowledgments
This work was supported by the Regional and Global Climate Modeling Program and the Earth System Modeling Program of the Office of Biological and Environmental Research in the Department of Energy Office of Science under contract number DE-AC02-05CH11231. NCEP Reanalysis data provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their Web site at http://www.esrl.noaa.gov/psd/. The (NARCCAP) for provided the data used in this paper through the Earth System Grid data portal at http://www.earthsystemgrid.org. NARCCAP is funded by the National Science Foundation, the US Department of Energy, the National Oceanic and Atmospheric Administration, and the US Environmental Protection Agency Office of Research and Development. CPC US Unified Precipitation data is provided by the NOAA/OAR/ESRL PSD, Boulder, Colorado, USA, from their web site at http://www.cdc.noaa.gov/. The author wishes to thank Charles Doutriaux, Peter Gleckler and Karl Taylor (Lawrence Livermore National Laboratory) with their help in producing the performance portraits and Taylor diagrams.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Appendix: generalized extreme value distribution
Appendix: generalized extreme value distribution
GEV theory is an asymptotic treatment of the tails of distributions with relatively few restrictions on its validity (Coles 2001; Castillo, et al. 2004). Hence, GEV theory has broad applicability to climate and other natural systems. The GEV distribution, F(x), is a three parameter function,
where ξ, α and k are called the location, scale and shape factors. The Gumbel distribution is a special case where the shape parameter, k, is zero. Formally, F(x) is the limiting cumulative distribution function of the maxima of a sample of independently and identically distributed random variables (Leadbetter et al. 1983). The three parameters of the GEV distribution may be quickly and accurately estimated from a sample of extreme values using a technique based on L-moments (Hosking and Wallis 1997) or a number of other techniques such as maximum likelhood. Here, F(x) represents the probability that the annual maximum of daily mean precipitation is less than x.
By further considering the tail of the appropriate GEV distribution function, one is truly describing rare events. The return value of a random variable, X T is that value which is exceeded, on average, once in a period of time, T. For example, when considering annual maxima of daily averaged variables, there is a 1/T chance of any daily average exceeding X T in a given year (where T is in years). Formally, this is straightforwardly defined as
where T 0 is a characteristic time whose value is 1 if T is measured in years. Solving for X T using the above definition of the GEV distribution yields (Castillo et al. 2004),
Hence, return values of annual or seasonal extrema are readily obtained by this inversion of the GEV distribution function after its three parameters have been estimated.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Wehner, M.F. Very extreme seasonal precipitation in the NARCCAP ensemble: model performance and projections. Clim Dyn 40, 59–80 (2013). https://doi.org/10.1007/s00382-012-1393-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-012-1393-1