Interpretation of the positive low-cloud feedback predicted by a climate model under global warming

Abstract

The response of low-level clouds to climate change has been identified as a major contributor to the uncertainty in climate sensitivity estimates among climate models. By analyzing the behaviour of low-level clouds in a hierarchy of models (coupled ocean-atmosphere model, atmospheric general circulation model, aqua-planet model, single-column model) using the same physical parameterizations, this study proposes an interpretation of the strong positive low-cloud feedback predicted by the IPSL-CM5A climate model under climate change. In a warmer climate, the model predicts an enhanced clear-sky radiative cooling, stronger surface turbulent fluxes, a deepening and a drying of the planetary boundary layer, and a decrease of tropical low-clouds in regimes of weak subsidence. We show that the decrease of low-level clouds critically depends on the change in the vertical advection of moist static energy from the free troposphere to the boundary-layer. This change is dominated by variations in the vertical gradient of moist static energy between the surface and the free troposphere just above the boundary-layer. In a warmer climate, the thermodynamical relationship of Clausius-Clapeyron increases this vertical gradient, and then the import by large-scale subsidence of low moist static energy and dry air into the boundary layer. This results in a decrease of the low-level cloudiness and in a weakening of the radiative cooling of the boundary layer by low-level clouds. The energetic framework proposed in this study might help to interpret inter-model differences in low-cloud feedbacks under climate change.

1 Introduction

As reported by the 4th Assessment Report (AR4) of the Intergovernmental Panel on Climate Change, current climate models still exhibit a wide range of climate sensitivity estimates (Solomon et al. 2007). Inter-model differences in cloud-climate feedbacks remain the main cause of these inter-model differences (Soden and Held 2006), with a large contribution from low-level cloud feedbacks (Bony and Dufresne 2005; Bony et al. 2006; Webb et al. 2006). The relative credibility of the different low-cloud feedbacks predicted by climate models has not been firmly established so far, although an observational study combined with an analysis of model simulations suggests some evidence for a positive low-level cloud feedback (Clement et al. 2009).

The difficulty of assessing the credibility of low-cloud feedbacks in climate models stems in part from the large number of processes and scales potentially involved in these feedbacks. Identifying and prioritizing better the primary physical controls of low-cloud feedbacks, at least in the world of climate models, would help to design relevant targeted process-oriented observational tests to assess these feedbacks. With this motivation in mind, the aim of this study is to analyze the physical mechanisms that primarily control the low-cloud feedback predicted by the IPSL-CM5A climate model, a model participating both in the Coupled Models Intercomparison Project Phase 3 (CMIP3, Meehl et al. 2007) and Phase 5 (CMIP5, Taylor et al. submitted) and characterized by a strongly positive cloud feedback (Soden and Held 2006) and a high climate sensitivity (Randall et al. 2007). The strong cloud feedback of this model originating mostly from low-latitudes, we will focus here on the analysis of the model cloud response to global warming in the tropics.

To identify the physical mechanisms likely to control low-level cloud feedbacks at first order, one approach consists in using simple or conceptual models whose physical characteristics can be readily comprehended (e.g. Miller 1997; Larson et al. 1999). However this approach may not necessarily be relevant to understand the cloud feedbacks that actually operate in climate models. An in-depth analysis of climate model outputs such as that undergone by Wyant et al. (2009) may better reveal the mechanisms at work in complex models. However, there are so many processes potentially involved in the control of low-cloud feedbacks in coupled ocean-atmosphere general circulation models (OAGCMs) that such an analysis remains difficult.

To facilitate this analysis, our approach consists in analyzing the response of tropical clouds to external forcings in several simulations performed with the same set of physical parameterizations but over a range of configurations more or less idealized: coupled ocean-atmosphere simulations run in a realistic configuration, atmosphere-only simulations, aqua-planet simulations, and one-dimensional simulations. Previous studies have shown the benefit of such an approach. For instance, by comparing three-dimensional (3D) atmospheric simulations with idealized simulations from a single-column model (SCM), Zhang and Bretherton (2008) could unravel the role of different physical parameterizations in controlling the low-cloud feedback in climate change; by comparing aquaplanet and realistic configurations of three climate models, Medeiros et al. (2008) showed that the response of shallow cumulus clouds to global warming was the primary cause of inter-model differences in cloud feedbacks among these models. Here, we will consider an even larger hierarchy of models to interpret the major characteristics of the low-cloud response to climate change predicted by the IPSL OAGCM.

Section 2 provides a brief description of the physical parameterizations used in the IPSL-CM5A OAGCM, and presents the main characteristics of the cloud response to climate change predicted by this model in CMIP5 coupled simulations. Section 3 compares the model cloud response to prescribed forcings in a hierarchy of model experiments and configurations and shows that major features of the cloud response to climate change found in OAGCM simulations can be reproduced in a one-dimensional (1D) framework. Section 4 investigates the physical mechanisms responsible for this response and Sect. 5 presents an analysis of the moist static energy (MSE) budget to provide an alternative interpretation of the IPSL results and suggest a more general mechanism of low-cloud feedback. Concluding remarks and perspectives are given in Sect. 6.

2 The cloud response to climate change predicted by the IPSL-CM5A-LR OAGCM

2.1 Brief description of the IPSL-CM5A-LR OAGCM

The IPSL-CM5A-LR OAGCM is the low-resolution version of the IPSL-CM5A model version used in CMIP5. Its atmospheric component, referred to as LMDZ4 (Hourdin et al. 2006), is largely similar to the one used in the IPSL-CM4 OAGCM of CMIP3 (Marti et al. 2005, 2010), except that both the vertical and horizontal resolutions have been improved (from 19 vertical levels and 3.7° × 2.5° longitude/latitude resolution in IPSL-CM4 to 39 vertical levels including 8 levels below 2 km- and 2.5° × 1.875° longitude/latitude resolution in IPSL-CM5A-LR, respectively), and that it can now be coupled to biogeochemical components so as to form the IPSL Earth System Model. ¹ More information about the IPSL-CM5A-LR (or IPSL-CM4) OAGCM can be found in Dufresne et al. (submitted).

Clouds are parameterized through a statistical cloud scheme describing the subgrid-scale variability of total water within each mesh of the model through a generalized log-normal Probability Density Function (PDF) bounded by zero on the lower side (Bony and Emanuel 2001). In (deep and shallow) convective situations, the statistical moments of this PDF are diagnosed from the in-cloud water content predicted in convective updrafts by the Emanuel parameterization (Emanuel 1991), modified by Grandpeix et al. (2004) and from the large-scale relative humidity field (Bony and Emanuel 2001). The skewness of the generalized log-normal PDF, which depends on the ratio between the variance and the mean of total water, is close to zero at low levels (therefore the PDF is close to a gaussian) but becomes more and more positive as height increases. A non-convective cloudiness is also predicted by the model using the same PDF but by computing the statistical moments of this PDF in a more ad-hoc fashion, by assuming that the total water variance is proportional to the mean total water, with a proportionality coefficient that varies linearly with pressure from 0.05 near the surface to 0.33 at 300 hPa (Hourdin et al. 2006). Two cloud schemes are called at each time step, and the maximum cloud fraction of the two schemes is used in radiation calculations. More information about the model physics can be found in Hourdin et al. (2006).

2.2 Overview of the cloud response to climate change

The climate sensitivity of the IPSL-CM5A-LR OAGCM is similar to that of IPSL-CM4. With an Equilibrium Climate Sensitivity of 4.4 K and a Transient Climate Response of 2.1 K (Fig. 1), this model ranges among the highest-sensitivity climate models of CMIP3 (Randall et al. 2007). A quantitative analysis of its radiative forcing and feedbacks shows that this high climate sensitivity stems from a strongly positive cloud feedback (Soden and Held 2006; Dufresne and Bony 2008). This strong feedback is associated with a large increase (in absolute sense) of the global NET (longwave + shortwave) Cloud Radiative Forcing (CRF) at the top of the atmosphere (by 0.5 W/m²/K, Table 1), which is dominated by the change in the shortwave (SW) component of the CRF (+1.3 W/m²/K). This weakening of the cooling effect of clouds as climate gets warmer arises mostly from low-latitudes (the change in SW CRF is more than two times larger in the tropics than in the extratropics) and is associated with a decrease of the cloudiness, especially of low-level clouds (Fig. 2).

Fig. 1

Time evolution of the globally-averaged change in surface temperature (a, in K), of the tropically-averaged change in LW (markers), SW (dashed line) and NET (solid line) cloud radiative forcing (b, in W.m⁻²), and of the tropically-averaged change in low-level cloud fraction (c, in %). Anomalies are computed for the so-called 1pctCO2 simulation (in which the CO₂ concentration increases by 1% per year) of the IPSL-CM5A-LR coupled ocean-atmosphere model, taking the first 10 years of the simulation as reference (5-month running mean)

Table 1 Global, tropical (30°S–30°N), and extra-tropical (90°S–30°S + 30°N–90°N) averages of changes in surface temperature, CRF components and low-level cloudiness predicted by the IPSL-CM5A-LR coupled model under climate change (changes correspond to the difference between the end and the beginning of the 1pctCO2 simulation)

Fig. 2

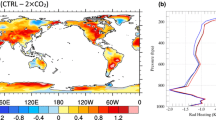
Left Low-level cloud fraction (a, in %), SW CRF (c, in W.m⁻²) and LW CRF (e, in W.m⁻²) averaged over the first 20 years of the 1pctCO2 simulation from the IPSL-CM5A-LR coupled ocean-atmosphere model. Right change in the same variables between the simulation at the time of CO₂ doubling (20-year average centered around the 70th year) and the beginning of the simulation

Many cloud regimes, ranging from deep convective to stratiform low-level clouds, may contribute to this change in tropically-averaged SW CRF. To determine their relative contribution, we use a simple compositing methodology (Bony et al. 2004) which consists in decomposing the large-scale atmospheric circulation in a series of dynamical regimes defined from the monthly large-scale vertical velocity at 500 hPa (ω). Within this framework, positive (negative) values of ω correspond to regimes of large-scale subsidence (convective regimes, respectively), and the PDF of ω is a measure of the statistical weight of each regime within the tropics (30°S–30°N). If C _ω is a composite of a geophysical field C (e.g. the SW CRF) in a regime defined by ω, and P _ω the PDF for this regime, the tropically-averaged C, noted $\bar{C}$, may then be defined as: $\bar{C} = \int_\omega P_\omega C_\omega d\omega$. The change in $\bar{C}$ may thus be linearly decomposed into three terms: a “dynamic” component related to the change in the large-scale atmospheric circulation ($\int_\omega C_\omega \delta P_\omega d\omega$), a “thermodynamic” component related to the change in C _ω for a given circulation regime ($\int_\omega P_\omega \delta C_\omega d\omega$), and a term of co-variation. The quantification of these different terms shows that, as in other models (e.g. Bony et al. 2004; Medeiros et al. 2008), the thermodynamic component largely dominates the tropically-averaged change in SW and NET CRF. This component accounts for the change in radiative cloud properties in each dynamical regime weighted by the PDF of this regime. As discussed in Bony et al. (2004), since the PDF is maximum in regimes of weak subsidence (for ω around 20 hPa/day), small changes in cloud properties within this regime can influence very strongly the tropically-averaged radiation budget owing to their large statistical weight.

The vertical profile of cloud fraction simulated by the IPSL-CM5A-LR OAGCM in regimes of weak subsidence (ω = 20 hPa/day), and its change under global warming are shown in Fig. 3. The model simulates a maximum cloud fraction (about 20 %) around 950 hPa, i.e. 0.6 km, thus well below the top of the PBL which occurs around 1 km. It is also at this level that the model predicts the largest decrease of the cloud fraction (and cloud water, now shown) in coupled simulations where CO₂ increases by 1 %/year. The aim of the following sections will be to analyze and to understand the origin of this change in low-level cloudiness.

Fig. 3

Vertical profile of cloud fraction (in %) predicted by the IPSL-CM5A-LR OAGCM in regimes of weak subsidence (ω₅₀₀ = 20 hPa/day) in the current climate (left) and its change under global warming at the time of CO₂ doubling (right)

3 Hierarchy of model configurations and experiments

3.1 Idealized atmospheric GCM experiments

The response of clouds to CO₂ increase and associated global warming in coupled ocean-atmosphere experiments may result from the interaction of a myriad of physical and dynamical processes, purely atmospheric and/or involving coupled interactions between the ocean and the atmosphere. To simplify the analysis and identify the dominant processes, we now analyze the response of clouds to a range of prescribed perturbations in model experiments run with exactly the same physical package but using different configurations.

One configuration consists in atmosphere-only experiments following the protocol of CMIP5 experiment #3.3.² In this experiment, commonly referred to as Atmospheric Model Intercomparison Project (AMIP) experiment (Gates 1992), the atmospheric component of the coupled ocean-atmosphere model is used in isolation using Sea Surface Temperatures (SST) prescribed from observations over the period 1979–2008. To distinguish the relative role of CO₂ increase and global warming in cloud changes, additional atmospheric experiments forced either by a globally uniform 4 K increase in SST (CFMIP2/CMIP5 experiment #6.8 referred to as AMIP4K) or by a prescribed quadrupling of the atmospheric CO₂ concentration (CFMIP2/CMIP5 experiments #6.5 referred to as AMIP4xCO2) are also performed.³

Aqua-planet experiments are also performed, in which the atmospheric model is run in perpetual equinox conditions using a specified, time-invariant distribution of SST zonally-uniform and symmetrical to the equator [the so-called “QOBS” distribution proposed by Neale and Hoskins (2000)]. These experiments run without any season nor land-atmosphere or ocean-atmosphere interactions, allow us to examine the response of clouds in a highly idealized framework and thus to assess the robustness of some predicted features. Aquaplanet experiments in which CO₂ is quadrupled ("Aqua4xCO2”) or in which the SST is uniformly increased by 4 K (“Aqua4K”) are also performed. These experiments correspond to the CFMIP2/CMIP5 experiments #6.7a, #6.7b and #6.7c, respectively.

The tropically-averaged change in CRF associated with the different experiments is given in Table 2. As in the OAGCM experiment, the change in NET CRF is dominated by the change in SW CRF. In all experiments, the change in SW CRF is also dominated by the thermodynamic component, which is itself dominated by the change in cloudiness that occurs in weak subsidence regimes (not shown). The vertical profile of cloud fraction simulated by the model in weak subsidence regimes in AMIP and aqua-planet configurations (Fig. 4) resemble very much that predicted in the OAGCM (Fig. 3), with however a slightly smaller cloud fraction at 950 hPa (about 13 vs. 20%), and a slightly larger cloudiness around 800 hPa in the aqua-planet configuration than in the more realistic AMIP or OAGCM configurations. The change in cloudiness between +4K and control experiments in AMIP and aqua-planet configurations are of same order as those found in OAGCM experiments (once normalized by the temperature change, which is roughly twice as large in +4K experiments than in the 1% CO₂ experiment at the time of CO₂ doubling), and occur at the same level. Note that these absolute changes are relative to their current climatological cloud profiles, which are slightly different in the three model configurations. In all configurations, the relative humidity decreases within the cloud layer and increases at the top of the boundary layer and above (Fig. 5), in association with an enhanced shallow convective activity. The response of clouds to the CO₂ radiative effect largely differs from the response to temperature change: both in AMIP and aqua-planet experiments, the cloud fraction changes little with CO₂, and exhibits only a weak increase around 950 hPa and a weak decrease around 800 hPa (Fig. 4).

Table 2 Tropically-averaged change in ocean surface temperature, CRF components and low-level cloudiness predicted by the atmospheric component of the IPSL-CM5A-LR climate model in AMIP and a aqua-planet simulations in uniform surface warming (+4K) experiments and in 4xCO2 experiments

Fig. 4

Vertical profile of cloud fraction (in %) predicted by the atmospheric IPSL-CM5A-LR AGCM in regimes of weak subsidence (ω₅₀₀ = 20 hPa/day) in AMIP (black lines) and aqua-planet (grey lines) simulations of the present-day climate (left) and in +4K (solid lines) or 4xCO2 (dotted lines) experiments (right)

Fig. 5

Same as Fig. 4 but for the relative humidity profile

Three main conclusions arise from this series of experiments: (1) the response of low-level clouds to temperature and CO₂ is similar in AMIP and aqua-planet experiments, suggesting that it is controlled by robust physical processes independent on their exact geographical distribution, and independent on land-surface processes at first order; (2) low-level clouds exhibit opposite responses to surface ocean warming and CO₂ radiative forcing: the former induces a decrease of low-level clouds and a weakening of their radiative effects while the latter induces an increase of low-level clouds and an enhanced cooling effect of clouds on climate (3) the response of clouds to climate change experiments performed with ocean-atmosphere coupling and associated with both surface warming and CO₂ increase is qualitatively and quantitatively much more consistent with the response of clouds to SST change, than to the response to CO₂ increase. It suggests that in the IPSL model, and contrary to some other models (Gregory and Webb 2008), the tropospheric adjustment to CO₂ radiative forcing exerts a much weaker impact on boundary-layer clouds than surface temperature changes. The sensitivity of low-level clouds to SST changes may stem from local and/or remote influences. To examine how much local processes may be responsible for this sensitivity, we now go one step further in the model hierarchy by considering Single Column Model (SCM) simulations forced by large-scale forcings representative of weak subsidence conditions. These simulations are run with exactly the same physical parameterizations as GCM experiments previously discussed.

3.2 Idealized Single-Column Simulations

To investigate the response of tropical low-clouds to climate change, we use the CFMIP-GCSS Intercomparison of Large Eddy Models and Single Column Models (CGILS) framework: the aim of this community project is to evaluate subtropical marine boundary layer cloud feedback processes in GCMs and in high-resolution process models using a set of idealized large-scale dynamical conditions.⁴ CGILS focuses on three cases of boundary-layer clouds occurring along a transect ranging from California to Hawaii (Teixeira et al. 2011) and representative of stratus, stratocumulus and shallow cumulus cloud types (Karlsson et al. 2010). For each case, idealized large-scale conditions representative of the present-day climate are derived from European Centre for Medium-Range Weather Forecasts (ECMWF) analysis, and idealized large-scale forcings representative of global warming conditions are derived by prescribing a +2 K SST increase and by assuming that the tropical temperature profile follows a moist adiabat, that the relative humidity remains constant, that profiles of horizontal heat and moisture advection are unchanged, and that large-scale subsidence is changed so as to balance the radiative cooling above the boundary layer (Zhang and Bretherton 2008). Climate change conditions are thus associated with a warmer, more stable atmosphere and a weakened vertical motion.

In this study, we focus on the so-called “S6” CGILS case, which corresponds to large-scale conditions very similar to those of the ω = 20 hPa/day dynamical regime (especially in terms of SST and vertical velocity profile). SCM simulations are performed for an SST of 298.8 K, a surface pressure of 1,014 hPa and a mean solar irradiance of 448.1 W/m², and they are initialized by specified temperature, humidity and wind conditions. As recommended by CGILS, a relaxation towards a specified temperature profile is applied to the predicted temperature profile between 600 hPa and the top of the atmosphere. The simulations are run for 200 days but a steady state is reached after about 20 days.

The time evolution of the vertical profile of cloud fraction predicted by the IPSL SCM is shown in Fig. 6a, together with the mean profile for present-day condition and its change under idealized climate warming. The SCM simulation exhibits a maximum cloud fraction (of about 25%) around 850 hPa with a secondary maximum around 950 hPa, and the cloud response to SST increase consists in a decrease of both cloud layers by a few percent. Although corresponding to similar large-scale conditions on the monthly time scale, these results thus differ considerably from the robust GCM characteristics associated with weak subsidence regimes (Fig. 4). How to interpret this difference?

Fig. 6

Left Time evolution of the cloud fraction simulated by the IPSL-CM5A Single-Column Model under so-called CGILS-S6 large-scale forcings (see text) with (a) and without (b) stochastic forcing applied on the large-scale vertical velocity. Right Time-averaged profile of cloud fraction simulated for the CGILS-S6 case in the Control experiment and its change under +2K experiments. Results are shown with (a) and without (b) stochastic forcing

3.3 Stochastic forcing

The examination of the time evolution of aquaplanet simulations in single geographical points belonging to the weak subsidence regime (monthly ω = 20 hPa/day) reveals a large high-frequency variability, with an alternance of shallow (and sometimes even deep) convection and suppressed conditions (Fig. 7). This variability, related to some internal synoptic variability of the atmosphere such as tropical waves, induces an alternance of cloud layers between 1,000 and 750 hPa, with a maximum occurence and amount at 950 hPa. The high-frequency variance of the GCM large-scale vertical velocity in regimes of weak subsidence is maximum in the upper troposphere, in agreement with NCEP2 meteorological reanalyses (Fig. 8). To investigate the influence that this high-frequency variability might have on the mean state, and also to reduce the proneness of the model to “grid-locking” the simulated cloud layers at particular vertical levels, especially near the trade inversion, we apply at each time step a stochastic forcing on the prescribed CGILS vertical velocity profile. For this purpose, we impose a white noise (of zero mean) that has the same variance as the vertical velocity profile of aqua-planet simulations in weak subsidence regimes, and we assume that stochastic fluctuations of the large-scale vertical velocity are vertically coherent (Fig. 8).

Fig. 7

Hourly sampling (during 1 month) of the vertical profile of cloud fraction (in %) derived from aqua-planet GCM outputs in a subtropical region of weak subsidence (left). The time average of this vertical profile is shown on the right

Fig. 8

Mean (thick lines) and standard deviation (dashed lines) of the vertical profile of large-scale vertical velocity derived from aqua-planet AGCM simulations (full) and the 6-hourly NCEP2 re-analysis (square markers) in regimes of weak subsidence

SCM simulations with a time-varying large-scale forcing (Fig. 6b) differ considerably from those with a stationary forcing (Fig. 6a), and the time-averaged cloud fraction obtained with transient forcing is much more consistent with GCM simulations (Fig. 4) than that obtained with stationary forcing. In particular, with time-varying forcing the maximum cloud fraction occurs at 950 hPa as in present-day GCM experiments, while it occurs at 800 hPa with stationary forcing. Idealized climate change experiments associated with a prescribed +2K and performed by applying a stochastic forcing on the perturbed vertical velocity profile (assuming that the variance at each vertical level remains similar) predict time-averaged changes in cloud fraction that qualitatively resemble those predicted in GCM experiments (Fig. 4), with however a larger magnitude. An additional SCM experiment with stochastic forcing in which the atmospheric CO₂ concentration is deliberately quadrupled (all other large-scale forcings remaining to their Control values) predicts a slight increase of the low-level cloud fraction and hence a negative cloud-radiative response (Table 3, experiment N) consistent with three-dimensional AMIP and aqua-planet 4xCO2 experiments (Fig. 4).

Table 3 Change in the top-of-atmosphere CRF (CRF _TOA ), in the tropospheric CRF (ACRF), in surface turbulent fluxes (SF latent plus sensible heat fluxes), and in the boundary-layer MSE vertical advection term (BVA, see text) obtained in different CGILS-S6 experiments (+2K-control) performed with the IPSL-CM5A SCM without any temperature relaxation in the upper troposphere

These results show that SCM simulations forced by CGILS large-scale forcings together with a white stochastic forcing qualitatively reproduce main features of the vertical cloud distribution predicted by the GCM, both under present-day conditions and climate change. In the rest of this study, we thus use stochastically-forced SCM simulations to further interpret the physical mechanisms that control the low-cloud response to external perturbations in the IPSL model.

4 Mechanisms responsible for the low-cloud response to external perturbations

4.1 Relative influence of the different forcings

In the CGILS framework, idealized climate change conditions are expressed through a change in SST, in the large-scale velocity profile, and in horizontal large-scale advections of temperature and moisture. In addition, the free-tropospheric temperature profile is relaxed towards a pre-defined, prescribed temperature profile. This relaxation of the free-trospospheric temperature in subtropical regions is meant to mimic the effect of gravity waves on the horizontal homogeneization of the tropical temperature above the boundary layer. To perform sensitivity tests aimed at unraveling the influence of different physical mechanisms on the subtropical low-cloud response, we deliberately remove it. However, the mean vertical profile of cloud fraction (Fig. 6b) obtained with and without temperature relaxation, as well as its response to climate change, are very close to each other (not shown).

A series of experiments is performed, in which individual climate change perturbations are applied one by one, and compared with the “Control” experiment (a SCM simulation forced by CGILS idealized forcings associated with present-day conditions, together with stochastic forcing and without temperature relaxation in the free troposphere). The radiative cloud response to these different forcings is quantified through the change in top-of-atmosphere (TOA) CRF and in atmospheric CRF (ACRF), defined as the difference between the CRF at TOA and at the surface. When all climate change forcings are applied (experiment A), the TOA CRF is weakened by about 13 W/m² (the TOA CRF being negative in the current climate, a positive anomaly corresponds to a weakening), and the ACRF (which is also negative in the current climate) is also weakened by about half as much (Table 3). When applying only the +2K SST perturbation (experiment B), the cloud radiative response is very close, albeit slightly weaker, to that obtained in experiment A. Applying only the change in vertical velocity (experiment C) also contributes to weaken the CRF and ACRF, but to a much lesser extent than in experiments A and B. Changes in horizontal temperature and moisture advections have either an opposite influence on CRF and ACRF (experiment D), or a weak influence (experiment E) comparable to that of experiment C. These results suggest that the change in SST constitutes the primary driver of the cloud radiative response in this subtropical cloud regime, and that other forcings related to dynamical changes have a secondary influence. These findings confirm that in our model, the subtropical cloud response to climate change is more driven by thermodynamical processes associated with SST changes, than by dynamical changes.

Two main physical processes dependent on surface temperature are likely to contribute to the response of clouds to SST: turbulence and radiation. Since both are related to each other through energy conservation (for given large-scale forcings, the source of energy of the atmosphere comes from surface turbulent fluxes, and the sink of energy is ensured by radiative cooling), we will focus on one of them only: the effect of SST changes on atmospheric radiative cooling, and its impact on the cloud distribution.

4.2 Influence of clear-sky radiative cooling changes

The increase in SST induces a warming and a moistening of the troposphere, which lead to an enhanced cooling of the atmosphere by clear-sky radiation (Fig. 9). To examine how much this change in clear-sky radiative cooling might contribute to the cloud response to SST, we repeat control and climate change SCM experiments by using a prescribed, stationary clear-sky radiative cooling (referred to as R ₀ and R′₀ for present-day and +2K climate conditions, respectively) instead of an interactive clear-sky radiative cooling. R ₀ and R′₀ are set to the time-averaged values of the clear-sky radiative cooling predicted in “Control” (Fig. 6b) and “Experiment A” (Table 3) SCM experiments, respectively.

Fig. 9

Change (relative to the control experiment) in the Clear-Sky radiative heating derived from +2K CGILS-S6 SCM experiments (a) and from AMIP (black) or aqua-planet (grey) AGCM experiments (b) in +4K (solid lines) or 4xCO2 (dotted lines) experiments in regimes of weak subsidence (ω₅₀₀ = 20 hPa/day). In CGILS and AGCM experiments associated with a uniform surface warming, the change in clear-sky radiative heating is normalized by the surface temperature change and thus expressed in K/day/K

The cloud-radiative response predicted by the SCM when substituting the time-varying clear-sky radiative cooling by a prescribed, time-invariant radiative cooling (R ₀ in present-day conditions and R′₀ in climate change), is fairly similar to that predicted by using an interactive clear-sky radiative cooling (compare experiments A and F in Table 3). Another experiment (G) identical to the “Control” experiment (present-day SST, horizontal advections, vertical velocity, etc) but imposing the clear-sky radiative cooling rate of the +2K experiment (R′₀) instead of R ₀ also predicts a cloud radiative response qualitatively similar to that obtained in actual climate change experiment (experiment A or F) when all forcings are applied. It seems therefore that the enhanced clear-sky radiative cooling associated with +2K conditions be sufficient to induce a low-cloud decrease and a low-cloud radiative response similar to that predicted by the IPSL model under climate change conditions. A similar conclusion is reached when considering the effect of 4xCO2 radiative forcing on low-level clouds and radiation (Table 3, experiment O). The reasons for the influence of the clear-sky radiative cooling on subtropical low-clouds is examined below.

The response of the clear-sky radiative cooling to global warming or 4xCO2 radiative forcing is shown in Fig. 9 for SCM and GCM (AMIP or aqua-planet) experiments: for each type of perturbation, both the vertically-integrated value and the vertical profile of the clear-sky radiative cooling change. To investigate the relative sensitivity of clouds to these two types of change, a series of experiments is performed in which a given perturbation of the vertically-integrated clear-sky radiative cooling ($\Updelta[R_0]$) is applied to the model, but distributed in different ways along the vertical (Table 3), localized either in the Upper Troposphere (UT, 100–400 hPa), in the Free Troposphere (FT, 400–700 hPa), in the Upper Cloud Layer (UCL, 900–700 hPa) or in the Cloud Layer (CL, surface-900 hPa). Experiments H and I show that the radiative response of clouds is as sensitive to the change in the vertically-averaged value ($\Updelta[R_0]$) as to the change in the vertical profile, and experiments J to M show that the response strongly depends on the altitude at which the perturbation is applied: low-level clouds decrease all the more that the clear-sky radiative perturbation is applied high in the troposphere. A perturbation applied within the boundary layer even enhances the low-level cloud fraction. These results suggest that the response of low-level clouds to a given radiative perturbation strongly depends on the change in the vertical atmospheric stratification associated with this perturbation. The reason for this influence is examined below by analyzing the energy budget of the troposphere.

5 An energetic interpretation of the low-cloud response to climate change

5.1 Moist static energy budget

Boundary-layer clouds exert a radiative cooling on the troposphere, which can be quantified through the so-called Atmospheric Cloud Radiative Forcing (ACRF). The ACRF is defined as the difference between the CRF at TOA and at the surface or, equivalently, as the vertically-integrated cloud perturbation of the tropospheric radiative cooling (defined as the all-sky minus clear-sky radiative heating rates) [R]−[R₀]:

$$ [ACRF] = [R] - [R_0] = \int\limits_{P_{SFC}}^{P_{toa}} (R-R_0) {\frac{dP} {g}} = CRF_{TOA} - CRF_{SFC} $$

(1)

The change in ACRF induced by different perturbations being strongly correlated with the change in SW CRF at the top of the atmosphere (Fig. 10, Table 3) and with the change in low-level cloud fraction (not shown), it may be used as a proxy for the cloud-radiative response that we aim to interpret.

Fig. 10

Relationship between changes in the NET cloud radiative forcing at the top of the atmosphere (CRF _TOA ) and within the troposphere (ACRF) changes predicted in the series of SCM experiments described in Table 3. Colored markers correspond to changes in CRF predicted in weak subsidence regimes by the AGCM in AMIP (red) or aqua-planet (blue) configurations in +4K (triangles) and 4xCO2 (diamonds) experiments

To understand what controls the cloud-radiative response to a given perturbation, and interpret in particular the strong sensitivity of low-level clouds to changes in the vertical stratification of the atmosphere, we analyze the tropospheric moist static energy (MSE) defined as h = c _p T + g z + L q where T is the temperature, c _p is the specific heat at constant pressure, z is height, g is the gravitational acceleration, L is the latent heat of vaporization at 0°C, and q is the specific humidity. The vertically integrated budget of MSE (brackets refer to vertical averages) may be expressed as:

$$ (LH + SH) + [R] - \left[\omega {\frac{\partial h}{\partial P}}\right] - [\overrightarrow{V}.\overrightarrow{\nabla} h] = 0 $$

(2)

where LH and SH are surface turbulent fluxes of latent and sensible heat, respectively, $\overrightarrow{V}$ is the horizontal wind, and ω the large-scale vertical velocity. The ACRF may then be expressed as:

$$ [ACRF] = -[R_0] - (LH + SH) + \left[\omega {\frac{\partial h}{\partial P}}\right] + [\overrightarrow{V}.\overrightarrow{\nabla} h] $$

(3)

Through this equation, the dimensionality of the cloud-feedback problem may be reduced to a problem of four components. In regimes of large-scale subsidence, the MSE of the planetary boundary-layer is increased by surface turbulent fluxes, and decreased by the emission of clear-sky radiation and by the downward advection of low-MSE from the free troposphere (Eq. 2). The presence of clouds also contributes to lower the PBL MSE through radiative cooling (ACRF), as well as the horizontal MSE advection. For a given horizontal advection of MSE, Eq. 3 shows that the radiative effects of clouds and the downward advection of low MSE into the PBL both contribute and eventually compete to balance the combined effect of surface fluxes and clear-sky radiative cooling on the PBL energy budget. It also shows that a change in the vertical profiles of large-scale subsidence and atmospheric stratification may change the magnitude of the vertically-integrated downward advection term of MSE $[\omega{\frac{\partial h}{\partial P}}]$.

Figure 11 compares the perturbations of the different terms of Eq. 3 in SCM experiments (G, J, K, L and M) in which a given vertically-averaged clear-sky radiative cooling is applied to the model with different vertical distributions (Sect. 2). In response to an increased [R ₀], surface fluxes always increase, all the more that the radiative cooling is applied near the surface (experiment M). However, the vertical advection term of MSE substantially depends on the vertical distribution of the clear-sky radiative perturbation and appears to be primarily responsible for differences in the cloud response among the different experiments: when the radiative cooling perturbation is applied in the upper troposphere, the change in the vertical stratification of MSE (the vertical velocity profile remains unchanged in this experiment but the MSE strongly decreases above the PBL) induces a strong negative anomaly of the vertical advection term which is not compensated by the increase in surface fluxes and is associated with a decreased low-cloud cover and a weakened ACRF (positive anomaly) to ensure energy conservation. At the other extreme, when the increased clear-sky radiative cooling perturbation is applied within the low-cloud layer, the vertical gradient of MSE in the lower troposphere weakens, which makes the vertical advection of MSE less negative in the PBL and leads to an enhanced low-level cloud cover and cloud radiative cooling. These experiments suggest that the impact of an external perturbation on the low-cloud cover strongly depends on how this perturbation affects the MSE vertical gradient within the PBL.

Fig. 11

Decomposition of the ACRF change predicted in different SCM experiments (see Table 3) into different components using the moist static energy budget of Eq. 3: changes in the clear-sky radiative cooling (in blue), in surface turbulent fluxes (in pink), in horizontal MSE advection (in cyan) and vertical MSE advection (in black) are all expressed in W.m⁻². Their sum compensate the change in ACRF (in red)

5.2 Physical understanding of the relationship between MSE advection term and low-level clouds

To understand physically the correlation between changes in the vertical gradient of MSE and changes in the low-level cloud cover, we examine the vertical profile of MSE normalized by the near-surface MSE value (Fig. 12) in SCM and GCM experiments. In the subsidence regimes of the tropics, the atmosphere exhibits a minimum MSE above the PBL (around 700 hPa) and thus a negative vertical advection term of MSE (−ω ∂h/∂P) below this minimum and a positive term above. In a warmer climate (SCM experiment A), the PBL deepens, the minimum MSE occurs higher in altitude and the MSE contrast between the near-surface and minimum MSE values increases: this induces a change in the MSE vertical advection term which maximizes between 900 and 700 hPa. A similar behaviour is found in GCM experiments, both in realistic (AMIP) and aqua-planet configurations.

Fig. 12

Mean vertical profile of MSE (top) and MSE vertical advection (bottom) derived from single-column model simulations (left) and from AMIP (solid lines) or aqua-planet (black lines with markers) AGCM simulations (right) in weak-subsidence regimes (ω₅₀₀ = 20 hPa/day). Control-climate simulations are plotted with solid lines, and global warming experiments (+2K in the case of SCM simulations, +4K in the case of GCM simulations) with dashed lines. Note that to emphasize the vertical gradient in MSE (or the MSE deficit relative to the near surface 1,000 hPa), the vertical profiles of MSE corresponding to climate warming experiments have been translated by an amount equal to the MSE change at 1,000 hPa so that both profiles correspond to the same near-surface value. Colored lines show the (translated) vertical profiles of MSE that would be obtained in AMIP (red line) and aqua-planet (blue line) +4K experiments if the change of MSE was due only to temperature change through the Clausius-Clapeyron relationship (i.e. by assuming a constant relative humidity)

Equation 3 and SCM sensitivity experiments (Fig. 11) suggest some correlation between the low-cloud radiative response and the change in vertical MSE advection. Since the sensitivity of the latter to climate change perturbations is maximum at the top of the PBL, we consider the vertically-integrated MSE vertical advection term between 900 and 700 hPa, an index hereafter referred to as boundary-layer vertical advection term or BVA (BVA = $\int_{900\,{\rm hPa}}^{700\,{\rm hPa}} -\omega {\frac{\partial h}{\partial P}} {\frac{dP} {g}}$). Figure 13 shows that across the range of SCM and GCM experiments, the change in low-level cloudiness (characterized by the change in PBL cloud fraction at the vertical level where the cloud fraction is maximum, which typically occurs around 950 hPa) is well correlated with the change in BVA (R ² = 0.55 with point M and R ² = 0.81 without). In response to a large range of perturbations (including changes in SST, CO₂ or large-scale subsidence), the change in BVA thus appears to be the term of Eq. 3 that correlates best with the change in ACRF, both in SCM and GCM experiments (Fig. 13).

Fig. 13

Relationship between the change in low-clouds, characterized by the 950 hPa low-level cloud fraction (where the cloud fraction is maximum; left) or by the ACRF integrated from the surface to 500 hPa; right) and the change in the vertical advection of MSE at the top of the boundary-layer ($\Updelta BVA$, see text for more details) derived from the series of SCM experiments described in Table 3. Colored markers correspond to changes in low-cloud fraction and BVA predicted in weak subsidence regimes by the AGCM in AMIP (red) or aqua-planet (blue) configurations in +4K (triangles) and 4xCO2 (diamonds) experiments

The vertical advection of MSE being dependent on both the vertical velocity profile and the vertical gradient in MSE, it may be perturbed both by local (e.g. surface temperature changes) and remote changes. Those latters may be associated with a change in the large-scale atmospheric dynamics (change in ω) or with a change in the free-tropospheric temperature profile, which is mainly controlled by deep convective processes. To clarify the origin of the change in low-level clouds, we thus examine in the next section the reasons for the change in BVA in GCM experiments.

5.3 Interpretation of low-cloud changes in GCM experiments

GCM experiments associated with a uniform (4 K) SST increase exhibit a decrease of low-level clouds while those associated with a 4xCO2 radiative forcing exhibit an increase of low-level clouds (Sect. 3.1, Fig. 4). These opposite responses are also associated with opposite changes in the vertical advection term of MSE in the PBL (Fig. 13). To interpret these different changes in BVA, we decompose the change in the MSE vertical advection term in three components as following:

$$ \Updelta \left[-\omega {\frac{\partial h}{\partial P}}\right] = \left[-{\frac{\partial h}{\partial P}}\Updelta \omega\right] + \left[-\omega \Updelta {\frac{\partial h}{\partial P}}\right] + \left[-\Updelta \omega \Updelta {\frac{\partial h}{\partial P}}\right] $$

(4)

Both in +4 K and 4xCO₂ experiments, the second right-hand-term quantifying the contribution of changes in the MSE vertical gradient represents more than 75 % of the total change in the two atmospheric models. The impact of ω changes on BVA is thus of secondary importance in modulating BVA in these experiments.

The robust change in the MSE vertical gradient and in BVA in surface warming experiments (Fig. 12) results from two factors. On the one hand, the deepening of the PBL, which is consistent with the expected growth of a marine shallow cumulus boundary layer in response to increased surface turbulent fluxes (Medeiros et al. 2005; Stevens 2007), rises the height of minimum MSE and then makes the vertical advection term of MSE more negative around the top of the PBL. However, a second and even more robust explanation is related to the non-linearity of the thermodynamic relationship of Clausius-Clapeyron, which increases the specific humidity (and thus MSE) with temperature at a larger rate near the surface than at altitude (changes in relative humidity play a secondary role, Fig. 12b). This enhances the MSE vertical gradient between the surface and the height of minimum MSE and then strengthens the import by large-scale subsidence of low-MSE from the free troposphere down to the surface. This effect, together with the deepening of the PBL, make BVA more negative and decreases the low-cloud fraction.

6 Conclusion and discussion

Using a hierarchy of models has made it possible to understand the physical reasons for the strong positive cloud feedback predicted by the IPSL-CM5A coupled ocean-atmosphere model under climate change. This feedback results primarily from the decrease, in a warmer climate, of tropical low-level clouds that occur in regimes of weak subsidence (e.g. over the trade winds). This decrease constitutes a robust feature of the model under global warming, reproduced by atmosphere-only experiments forced by a prescribed surface ocean warming, both in realistic (AMIP) and aqua-planet configurations. It is also reproduced by SCM simulations forced by CGILS forcings representative of shallow-cumulus conditions, provided that a stochastic forcing (aimed to mimic the large high-frequency variability of these regimes) is added to the prescribed large-scale vertical velocity profile. The analysis of SCM and GCM simulations has made it possible to clarify the reasons for the decrease of low-level clouds under global warming, and the increase of low-level clouds to 4xCO2 radiative forcing.

Under global warming, turbulent fluxes at the ocean surface increase together with the clear-sky radiative cooling of the troposphere. This enhances shallow cumulus convection, and the upward transport of moisture towards the free troposphere. In parallel, the change in specific humidity resulting from the change in temperature through the non-linear thermodynamical relationship of Clausius-Clapeyron leads to a larger vertical gradient in humidity and MSE between the surface and the level of minimum MSE above the top of the PBL. This strengthens the import of low MSE from the free troposphere down to the PBL. The enhanced vertical advection of MSE lowers the MSE of the PBL, leading to a decreased low-level cloud fraction and a weakened radiative cooling of the PBL by cloud-radiative effects (which becomes “less necessary” to balance the energy budget). This mechanism is summarized in an idealized way in Fig. 14.

Fig. 14

Schematic of the physical mechanisms controlling the positive low-cloud feedback of the IPSL-CM5A-LR OAGCM in climate change. In the present-day climate, tropical marine low-clouds primarily occur in regimes of large-scale subsidence. In these regimes, the moist static energy (MSE) of the PBL is increased by surface turbulent fluxes, and decreased by clear-sky radiative cooling, cloud-radiative cooling, and by the downward advection of low MSE from the free troposphere (the typical profile of MSE deficit on the right -defined as the difference between the MSE profile and the 1,000 hPa MSE- shows that the MSE minimum occurs around 700–850 hPa in weak subsidence regimes). Shallow cumulus clouds contribute to the vertical transport of humidity from the PBL to the lower free troposphere, and deep convection controls the free tropospheric temperature profile of the tropical belt. In a warmer climate, the change in the moist-adiabatic stratification of the tropical atmosphere, the enhanced vertical transport of humidity by shallow convection and the deeper PBL due to enhanced surface fluxes all tend lead to a decrease of the vertical gradient of MSE. However, the non-linearity of the Clausius-Clapeyron relationship leads to a larger increase in specific humidity at high temperatures and low altitudes than at lower temperatures and higher altitudes. This leads to an enhanced vertical gradient of specific humidity and MSE between the PBL and the lower free troposphere, and thus an enhanced import of low-MSE and dry air from the free troposphere down to the PBL. This decreases the low-level cloud fraction and weakens the cloud radiative cooling within the PBL

The increases of surface turbulent fluxes and of clear-sky radiative cooling constitute robust features of global warming experiments (e.g. Zhang and Bretherton 2008; Wyant et al. 2009; Xu et al. 2010), and the increase in vertical gradients of MSE and moisture under climate change is likely to be robust across models owing to its large dependence at first order on the Clausius-Clapeyron relationship. However, the relative magnitude of the change in MSE vertical advection versus the change in surface turbulent fluxes and radiative cooling is controlled by several factors which may depend on the type of perturbation applied to the climate system, and on the physical parameterizations of atmospheric models. These factors include the change in large-scale vertical velocity, the change in the vertical stratification of the tropical atmosphere above the free troposphere (which is partly controlled by remote deep convective processes), and the change in the moistening of the free troposphere by shallow cumulus convection. This latter process is likely to be particularly critical since it may partly oppose the robust effect of the Clausius-Clapeyron relationship on the MSE vertical gradient. Combined with the ubiquitous occurrence of shallow cumulus clouds over tropical oceans, it suggests (as already emphasized by earlier studies such as Bony et al. 2004; Medeiros et al. 2008) that the representation of shallow cumulus convection by climate models and its response to global warming is particularly critical for climate sensitivity and should be thoroughly tested. The relative magnitude of changes in MSE vertical advection versus surface fluxes or radiative cooling may also depend on the representation of the mean present-day climate by GCMs. Depending on how the different climate models simulate the present climate, the change in large-scale atmospheric circulation and the vertical stratification of the tropical atmosphere, a given external perturbation may thus lead to different low-level cloud responses. This presumably explains the wide range of low-level cloud responses predicted by climate models under climate change (e.g. Bony and Dufresne 2005; Webb et al. 2006; Medeiros et al. 2008), and thus the large uncertainty in climate sensitivity.

In a recent study using a Large-Eddy Simulation (LES) model to investigate the response of shallow-cumulus clouds to global warming in a nearly-constant relative humidity atmosphere (Rieck et al. submitted), a warmer climate was found to be associated with enhanced surface fluxes, a deeper boundary layer, a decreased relative humidity within the cloud layer, and a decrease of the low-level cloud fraction. As part of the CGILS project (Zhang et al., in preparation), idealized simulations of low-level clouds and of their response to climate change will be performed by several SCMs, LES models and Cloud Resolving Models (CRMs). It will then be possible to assess the extent to which the physical processes identified here as playing a key role in the control of shallow cumulus cloud feebacks in a climate model are also at work in other climate models and in high-resolution, explicit cloud models. Inter-model differences in the response of low-level clouds to climate change may then be interpreted in the light of the present results.

This study proposes a framework that may guide future investigations of low-level cloud feedbacks using models or observations. In particular, it suggests that examining how low-level clouds (and shallow cumulus clouds in particular) respond to changes in the vertical profile of MSE, as well as changes in large-scale vertical velocity might help to constrain the low-level cloud feedback from observations. A recent observational study by Kubar et al. (2011) shows that the low-cloud frequency is well correlated with the difference in MSE between 700 hPa and the surface. These observations, combined with our finding that the vertical advection of MSE by large-scale subsidence also constitutes an important control of the low-level cloud cover in climate change, suggest that it might be possible in a near future to constrain low-level cloud feedbacks from observations, and then to assess which of the model low-cloud feedbacks are likely to be the most reliable. This is will be investigated as part of the analysis of CMIP5 simulations and will be reported in a future paper.