Abstract
We synthesize variability and trends in multiple analyses of Antarctic near-surface temperature representing several independent source datasets and spatially complete reconstructions, and place these into the broader context of the behavior of other components of the climate system during the past 30–50 years. Along with an annual-mean trend during the past 50 years of about 0.1°C/decade averaged over Antarctica, there is a distinct seasonality to the trends, with insignificant change (and even some cooling) in austral summer and autumn in East Antarctica, contrasting with warming in austral winter and spring. Apart from the Peninsula, the seasonal warming is largest and most significant in West Antarctica in the austral spring since the late 1970s. Concurrent trends in sea ice are independent evidence of the observed warming over West Antarctic, with the decrease in sea ice area in the Amundsen and Bellingshausen Seas congruent with at least 50% of the inland warming of West Antarctica. Trends in near surface winds and geopotential heights over the high-latitude South Pacific are consistent with a role for atmospheric forcing of the sea ice and air temperature anomalies. Most of the circulation trend projects onto the two Pacific South American (PSA) modes of atmospheric circulation variability, while the Southern Annular Mode lacks a positive trend in spring that would otherwise cause a cooling tendency. The largest circulation trend is associated with the PSA-1 mode, a wave-train extending from the tropics to the high Southern latitudes. The PSA-1 mode is significantly correlated with SSTs in the southwestern tropical and subtropical Pacific. The increased SSTs in this region, together with the observed increase in rainfall, suggest that anomalous deep convection has strengthened or increased the occurrence of the Rossby wave-train associated with PSA-1. This hypothesis is supported by results from two ensembles of SST-forced atmospheric general circulation model simulations. Finally, the implications of the seasonality, timing, and spatial patterns of Antarctic temperature trends with respect to interpreting the relative roles of stratospheric ozone depletion, SSTs and increased atmospheric concentrations of greenhouse gasses are discussed.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Studies of climate change over West Antarctica and the adjacent South Pacific are hampered by the paucity of long observational records and by the presence of large interannual to decadal-scale variability. There are no permanent research stations in the ~3,700 km distance along the Pacific sector from the Rothera and Faraday/Vernadsky stations on the western Antarctic Peninsula to the McMurdo and Scott Base stations near the western Ross Ice Shelf (Fig. 1). Nonetheless, monitoring and understanding climate change in this region is of critical importance for estimating the contribution of the Antarctic Ice Sheet to global sea level rise from the combination of changes in ice sheet dynamics and the surface mass balance (e.g. Pritchard et al. 2009; Rignot et al. 2008; Monaghan et al. 2006).
Map of Antarctica, indicating station locations (green circles) and regions discussed in the text. The background colorscale on land is the long-term SON seasonal mean near-surface temperature from the M10 dataset. The colorscale over the ocean region indicates the mean sea ice concentration for SON and the vectors indicate the SON mean 10 m wind vectors. The purple line marks the approximate boundary of WAIS and EAIS. The green line marks the approximate boundary of the WA sub-region of WAIS, which excludes the Peninsula and the large basin containing the South Pole
The sparse in situ observational network indicates rapid near-surface temperature increases on the Antarctic Peninsula, and no change or slight decreases across East Antarctica (Turner et al. 2005). This spatial pattern has been attributed to a trend towards the positive phase of the Southern Annular Mode (SAM) (e.g. Thompson and Solomon 2002; Marshall 2007), the leading mode of variability in the extra-tropical atmospheric circulation, characterized by atmospheric pressure anomalies of opposite sign between the polar latitudes and the mid-latitudes. The positive SAM trend, implying lower pressures over the polar latitudes and relatively higher pressures over mid-latitudes, has been most pronounced in the austral summer and autumn, and has been attributed to forcing by stratospheric ozone depletion, and to a lesser extent, increases in greenhouse gasses (e.g. Arblaster and Meehl 2006). The SAM trend has greatly influenced temperature trends in East Antarctica (Marshall 2007). On the Peninsula, the SAM trend appears to have played a key role in the summer warming on the eastern side, but a limited role in the strong winter warming on the western side (Roscoe et al. 2006; Marshall 2007).
Relatively few studies have focused on temperature trends west of the Peninsula due to the comparative remoteness of this area and to the even sparser observational network. The relation between the SAM index and temperatures in West Antarctica is somewhat weaker than with temperatures in East Antarctica (e.g. van den Broeke et al. 2006; Schneider et al. 2004; Kwok and Comiso 2002; Marshall 2007). Looking specifically at the observational relationship between stratospheric ozone depletion events and subsequent geopotential height anomalies, Neff et al. (2008) found a strong asymmetry about the continent. While coastal East Antarctic stations show detectable negative tropospheric geopotential height (and by inference, temperature) anomalies in summer following spring ozone depletion, South Pole, Halley and McMurdo stations show no such response. Thus, the signal of ozone depletion and the SAM is not uniform across the continent.
In addition to spatially varying SAM-temperature relationships, other factors contribute to the differences in climate signals of East and West Antarctica. The West Antarctic and South Pacific sector is strongly influenced by atmospheric circulation anomalies originating as Rossby wave-trains forced from deep convection anomalies over the tropical Pacific on intraseasonal, interannual (ENSO) and lower-frequency timescales (e.g. Mo and Higgins 1998; Mo 2000; Bromwich et al. 2004; Turner 2004; Schneider and Steig 2008; Garreaud and Battisti 1999; Gregory and Noone 2008). The region has relatively low-lying topography, allowing a stronger synoptic-scale influence on temperature variations than over the high, East Antarctic plateau (Bromwich and Wang 2008). The flux of moist static energy entering Antarctica is greatest in the 60°W to 150°W sector (Genthon and Krinner 1998). The prevailing direction of heat and moisture transport in this region is onshore; this is reflected in the large annual surface mass balance in coastal West Antarctica (e.g. van de Berg et al. 2006). A recent study using archives from a polar-adapted forecast model found that West Antarctica is subject to frequent excursions of warm and moist marine air masses originating from the Ross and Amundsen Seas (Nicolas and Bromwich 2010). The strong poleward atmospheric heat and moisture transport may be one reason why the West Antarctic and Peninsula climate appears to be more strongly coupled with regional sea ice concentration and extent anomalies than does the East Antarctic (e.g. Jacobs and Comiso 1997; Weatherly et al. 1991).
Recently, a number of methods have been used to address the sparse observational coverage of West Antarctic climate, including analysis of remote sensing data, interpolation of data from the sparse station network, and merging of in situ records. Steig et al. (2009) combined satellite-derived temperature data with station data to produce a gridded reconstruction of Antarctic temperatures spanning 1957–2006. They reported an annual warming of West Antarctica of 0.18°C/decade for 1957–2006, maximized in the austral winter and spring. Chapman and Walsh (2007) used a distance-weighted interpolation of station and oceanic records to produce a 1° × 1° gridded reconstruction for 1950–2002. Their maps showed warming across most of West Antarctica. Monaghan et al. (2008) used a kriging method to produce a 1° × 1° reconstruction for 1960–2005. They reported generally positive trends for most of West Antarctica, but none were statistically significant. However, the Monaghan et al. reconstruction updated for years 1998–2007 using a new record for Byrd station (80°S, 120°W) exhibits larger and statistically significant temperature trends for West Antarctica (Bromwich et al. 2008). The updated reconstruction shows warming of West Antarctica in all seasons, significant in the austral spring and summer, and is in better agreement with the Steig et al. (2009) reconstruction than the Monaghan et al. (2008) version was. Recently, O’Donnell et al. (2010) proposed alternative methodology for the Steig et al. (2009) reconstruction, suggesting an annual warming trend for West Antarctica of 0.06°C/decade or 0.10°C/decade for 1957–2006, depending on the algorithm used to account for spatial and temporal relationships of the station data and satellite data.
Proxy data from ice cores (e.g. Schneider and Steig 2008; Thomas et al. 2009) and boreholes (e.g. Barrett et al. 2009) have also been developed to infer West Antarctic climate variability and trends over the past 50–200 years. An average of the ice core water stable isotope timeseries from West Antarctica suggests persistent warming through the second half of the twentieth century (Schneider and Steig 2008), as do ice cores from the western side of the Antarctic Peninsula (e.g. Thomas et al. 2009). Inversions of borehole temperature profiles also show warming on low-frequency timescales (e.g. Barrett et al. 2009).
Although a wealth of new datasets has become available, each has its own intrinsic uncertainties due to observational coverage and to assumptions that must be made in the methodologies, and it is not obvious that all the results are in agreement with one another. For example, satellite-derived estimates based on thermal infrared measurements (e.g. Comiso 2000; Kwok and Comiso 2002; Schneider et al. 2004) provide broad spatial coverage, but depend on effective cloud masking, and provide at best a clear-sky dataset that is generally cold biased. The magnitude of the cloud and cold bias can vary spatially and seasonally, raising questions about the inter-regional and inter-seasonal comparability of trends. Automated weather stations (AWS) also fill in gaps where permanent research stations do not exist, and they can optimally provide measurements every 6 min (e.g. van den Broeke et al. 2006). However, it is notoriously difficult to maintain AWS in good working condition in the Antarctic. Moreover, over time AWS instruments can become buried in snow and bias the measurements. Only a handful of AWS have operated for at least 20 years, barely long enough to establish a significant trend in the Antarctic. When combining records to make a reconstruction, assumptions need to be made concerning selection criteria for the input data and the statistical methods to be used. Even with the generally large spatial coherence and correlation length scales of temperature anomalies at polar latitudes (e.g. Hansen et al. 1999; Chapman and Walsh 2007), none of the reconstruction methods can escape the basic limitation of few in situ observations in West Antarctica, and all exhibit less skill in this region compared with other regions of the continent.
Each of the three major reconstructions of Antarctic temperature (Chapman and Walsh 2007; Monaghan et al. 2008, 2009; Steig et al. 2009) used different methodologies and somewhat different source datasets, as discussed below. Additionally, global-scale interpolations of station data (e.g. Hansen et al. 1999, 2010) also provide Antarctic coverage. Moreover, other datasets from satellites include temperature retrievals from the Microwave Sounding Unit (MSU; Johanson and Fu 2007) and estimates of sea ice concentrations from passive microwave observations (e.g. Comiso and Nishio 2008; Cavalieri and Parkinson 2008). To date, these data have been largely discussed independently of one another, and have not necessarily reported consistent results.
The first goal of this study is to provide intercomparison of the datasets discussed above. To this end, we perform a synthesis of observational records to address the questions of whether there is consistency among datasets and significant trends in East and West Antarctica. Our strategy is to use many independent datasets and derived reconstructions, and to examine relationships among variables that are physically linked, such as temperature, sea ice concentration, and geopotential height. Evaluating the quality and consistency of atmospheric Reanalysis is not a goal of this study, but we use it as a secondary data source when no other suitable observations readily exist. The second goal of this study is to address two simple questions; “Why is warming over the past 30–50 years greater in West Antarctica than in East Antarctica?” and, “Why is austral spring (September–October–November: SON) the season of largest warming?” Addressing these questions requires investigation of the sea ice-air temperature relationship as well as revisiting the relationships of Antarctic temperature and sea ice anomalies with variability and trends in the extratropical atmospheric circulation.
This paper is organized as follows. In Sect. 2, we discuss our datasets and methods. Our results are presented in Sect. 3, which is separated into several subsections. We first present a broad overview of trends since ~1960 according to the major reconstructions, but the bulk of our analysis is focused on the 1979-present period due to increased observational coverage and the amplification of some of the trends. We analyze the covariance of the temperature and sea ice trends, and discuss how wind changes may force the latter. Next, we relate the circulation and wind trends to the large-scale modes of extratropical Southern Hemisphere (SH) atmospheric circulation, using a combination of empirical orthogonal function (EOF) and regression analysis. Finally, atmospheric model simulations with prescribed sea surface temperatures (SSTs) illuminate the role of SST trends in forcing the observed circulation trends. In Sect. 4, we provide a summary and discussion of our results.
2 Data and methods
2.1 Data
Our analysis draws upon five temperature and sea ice datasets that can be considered independent sources (Table 1). The primary source of Antarctic observational data is the Reference Antarctic Data for Environmental Research (READER) archive (Turner et al. 2004) that contains monthly mean observations of near surface temperature, surface pressure and upper-air measurements from Antarctic research stations. In addition to data from traditional research stations, the READER archive also contains measurements from several AWS. Here, we use monthly mean temperatures directly from 18 stations in the READER dataset (Fig. 1). We do not use the AWS data directly, but instead draw upon the AWS-based reconstruction of Steig et al. (2009).
The other three sets of independent data come from satellite-based measurements. Surface skin temperatures have been derived from the thermal infrared channels of the Advanced Very High Resolution Radiometer (AVHRR), as discussed by Comiso (2000). Since Comiso (2000), the AVHRR data have been periodically updated using improved methods of cloud masking. Here, we use the version of the monthly mean AVHRR data for 1982–2006 used by Steig et al. (2009). Tropospheric temperature data retrieved from the Microwave Sounding Unit (MSU) (Johanson and Fu 2007) are another valuable satellite-derived product for Antarctic studies. Although not the same quantity as surface temperatures, MSU data are useful for diagnosing the causes of Antarctic temperature trends. They also help to confirm some of the surface measurements. Due to the high elevation of the Antarctic ice sheet and to the cold, dry and thin polar atmosphere, up to 40% of the total MSU tropopspheric signal actually comes from the surface (Johanson and Fu 2007).
Finally, passive microwave brightness temperatures from various satellite platforms have been extensively used to derive estimates of sea ice concentration. Here, we do not use the brightness temperatures directly, but rather use the compilation of sea ice concentration of Hurrell et al. (2008). The Hurrell et al. dataset is a blend of optimally interpolated SSTs and sea ice (Reynolds et al. 2002) and of the HadISST (Rayner et al. 2003) datasets. The SH sea ice data are reliable since 1979, but suffer from poor observational coverage before 1979, and revert to climatology before 1974. Although several different algorithms have been used to derive sea ice concentrations from the satellite measurements, our analyses based on the Hurrell et al. (2008) data are consistent with previous studies. These studies have unanimously shown statistically significant decreases in sea ice concentration, extent and ice season duration in the Bellingshausen and Amundsen seas, contrasted with increases in sea ice concentration, extent and ice season duration in the Ross Sea (Comiso and Nishio 2008; Stammerjohn et al. 2008; Cavaleri and Parkinson 2008; Turner et al. 2009; Liu et al. 2004; Parkinson 2002). Here, the sea ice data are used to illuminate how the trends in sea ice concentration relate spatially and temporally to the trends in land temperatures.
We present results from several derived datasets that cannot be considered completely independent because they have source data in common. However, these datasets use different methodologies and different tolerances for interpolating across data-sparse regions. Familiar global datasets that we briefly consider include SSTs from HadSST2 (Rayner et al. 2006) and combined SST and land temperatures from HadCRUT3v (Brohan et al. 2006). A similar combined SST-land temperature dataset known as the NOAA merged temperature analysis is also assessed (Smith et al. 2008). Finally, we use the 1,200-km version of the GISTEMP analysis (Hansen et al. 1999, 2010). The GISTEMP product is noteworthy for our study because it uses station data from the READER archive and, unlike HadCRUT3v, makes interpolations across large distances, covering much of the Antarctic ice sheet and adjoining Southern Ocean. The GISTEMP analysis uses linear weights that decrease as a function of distance from a station observation. Essentially, each grid point observation in the GISTEMP analysis is a distance-weighted average of the station data within 1200 km. Similar to the Hurrell et al. (2008) analysis, SSTs in the GISTEMP analysis are a concatenation of the Hadley Centre analysis thru 1981 (Rayner et al. 2003) and of the satellite-based optimally interpolated SSTs (Reynolds et al. 2002) for 1982 to present. However, in the polar sea ice zones, GISTEMP extrapolates the land surface air temperature anomalies over the oceans to a radial distance of 1,200 km (Hansen et al. 2010). The use of READER data in the GISTEMP analysis makes it much more useful for our study than the NOAA and HadCRUT3v datasets. We found that the latter two datasets do not have substantial Antarctic data, and thus they are not considered further.
As mentioned above, a few studies have focused on reconstructions of temperatures solely across the Antarctic domain. All have used the station data from the READER archive. The Chapman and Walsh (2007) reconstruction (referred to below as CHAPMAN) is the most similar to GISTEMP in that it uses distance-weighted interpolation to fill in data voids on a regular 1° × 1° degree grid. It incorporates a relatively large number of in situ data from both manned and automated weather stations and ship and buoy SST measurements, covering a large domain including the Antarctic continent and extending across the Southern Ocean to ~45°S. The weights are based on correlation length scales that generally decrease exponentially as a function of distance, rather than linearly, and are not fixed as in the GISTEMP analysis. Temporal variance is lost because the interpolation procedure smoothes the original input data. Results in the trend maps (e.g. Fig. 3) adhere closely to the trends at the stations, but the magnitudes of the trends drops off as the radial distance from the station increases.
In contrast to the distance-weighted approach, Steig et al. (2009) and Monaghan et al. (2008) used covariance methods to establish spatial relationships among the observing stations and the regions to be infilled. The use of spatial information accounts for the effects of topography and the atmospheric circulation (including teleconnections) on temperature variability. The Monaghan et al. study used the correlation structure in the ERA-40 reanalysis (Uppala et al. 2005) to define the weights on the observational records that are applied at each gridbox on 1° × 1° degree regular grid with a kriging method. A scaling is applied to the interpolated anomalies to restore variance lost in the weighting scheme. A disadvantage is that the calibration and variance is subject to the inherent biases in the ERA-40 reanalysis (Bromwich et al. 2007). The original Monaghan et al. dataset has been revised by incorporating a new blended station and AWS record from Byrd (80°S, 120°W) (Byrd operated as a traditional research station for a period from the late 1950s to the mid 1970s.) (Bromwich et al. 2008). The reconstruction has been further extended through 2009 (A. Monaghan, personal communication, 2010). The revised and extended version (referred to as M10) is used in this study. Only the years 1998–2009 are different in the M10 version from the original version presented by Monaghan et al. (2008).
Steig et al. (2009) presented a reconstruction (referred to as STEIGv1) using a regularized expectation maximization algorithm (Schneider 2001) to assess the spatial covariance of temperature anomalies in the AVHRR satellite observations. The covariance patterns are statistically related to the anomalies in the READER station data records, and these relationships are used to infill the domain of the Antarctic continent prior to the period of the satellite coverage. A calibration/verification procedure was applied, withholding a period of satellite observations to test how the reconstruction performed in the withheld period. This has the advantage of allowing explicit verification statistics to be calculated, and the patterns reconstructed are physically recognizable (e.g. temperature anomaly patterns related to the SAM and ENSO). However, this choice of a limited number of spatial patterns effectively filters the data so that some variance is lost. Also of note is that the satellite network is limited to clear-sky observations and the surface anomalies may not be the same as the 2-m air temperature anomalies. However, because only large-scale, first-order patterns are reconstructed, similar patterns of spatial/temporal covariance are found in the station data alone (otherwise, there would be very little skill in the reconstruction).
Additionally, Steig et al. (2009) presented an alternative version based on data from automated weather stations (AWS), rather than the satellite data (referred to as SteigAWS). A third version of the Steig et al. (2009) reconstruction (referred to as STEIGv2) used linearly detrended AVHRR data to define the spatial covariance patterns. These two alternatives provide sensitivity tests of the reconstruction to trends in the satellite data, which have uncertainties due to clouds. The AWS version avoids satellite data entirely to test whether the same large-scale patterns can be obtained even with a sparse observational network. The Steig et al. data were produced on a polar stereographic grid with approximately 25 × 25 km resolution (except for the AWS reconstruction, which is only computed at the AWS locations). Here, we regrid the Steig et al. data to a 1° × 1° degree regular grid so that they are directly comparable with the Monaghan et al. and Chapman and Walsh data.
Additional data that we use to aid our interpretations include geopotential height and 10-m wind fields from the National Centers for Environmental Prediction, version 2 (NCEP2) reanalysis for 1979-2008 (Kanamitsu et al. 2002), obtained from the NOAA Earth Systems Research Laboratory (http://www.esrl.noaa.gov/psd/data/gridded/). To confirm that our interpretations are not dependent on the reanalysis dataset used, we also examined circulation trends in the ERA-40 (Uppala et al. 2005) and JRA-25 (Onogi et al. 2007) reanalysis datasets, and found similar results. For precipitation, we used the Global Precipitation Climatology Project, version 2.1 (GPCP) (Adler et al. 2003), obtained at the National Center for Atmospheric Research (NCAR) (http://www.cgd.ucar.edu/cas/catalog/satellite/gpcp/gpcp_v21.html).
2.2 Methods
We separate the Antarctic continent into four domains: All Antarctica (ALL), East Antarctic Ice Sheet (EAIS), West Antarctic Ice Sheet (WAIS), and West Antarctica (WA) (Fig. 1). These geographic separations are made according the glaciological basins of Vaughan et al. (1999), which are delineated on a 1° × 1° mask as described by Monaghan et al. (2006). To calculate ALL, EAIS, WA or WAIS timeseries, we apply area-weighting using the cosine of latitude to account for the smaller size of 1° × 1° grid boxes at higher latitudes. Note that by this glaciological definition, part of EAIS is actually in the Western Hemisphere, namely the sector from 0°W to ~30°W, due to the orientation of the Trans-Antarctic Mountains, which separate the ice sheets. WAIS also includes a basin that extends through a gap in the Trans-Antarctic Mountains to the South Pole; this basin was excluded from the WA area. WA also excludes the glaciological basins of the Peninsula. We include the major ice shelves. For our sea ice area calculations, we define the Amundsen and Bellingshausen Sea (ABS) as the region of the Southern Ocean from 60°W to 130°W and also apply area weighting. The Bellingshausen Sea is the area from 60°W to 90°W. When referring to longitudinal sectors in this paper (e.g. 60°W to 130°W), we proceed in a westward (i.e. counterclockwise) direction around the continent.
We focus our discussions and interpretations on features that we find to be robust across a range of datasets. Our calculations of the statistical significance of least-squares linear trends in timeseries are based on the two-sided t-test methodology and adjustment for autocorrelation reviewed and outlined by Santer et al. (2000). We adjusted both the sample size and the degrees of freedom for indexing of the critical t-value according to the lag-1 autocorrelation of the regression residuals. Annual trends are calculated by averaging the monthly mean anomalies together and fitting the regression to the annual average timeseries.
Finally, we present results from two 5-member ensembles of atmospheric model simulations. The model used for both ensembles is the NCAR Community Atmosphere Model, version 3 (CAM3), configured at T85 (1.4° latitude × 1.4° longitude) horizontal resolution (Hurrell et al. 2006). The first set of simulations, referred to as Global Atmosphere-Global Ocean (GOGA) experiments, are forced with prescribed SST and sea ice concentrations from the observational datasets of Hurrell et al. (2008) for 1979–2008, with different initial conditions for each ensemble member. The second set of simulations, referred to as Tropical Ocean-Global Atmosphere (TOGA) experiments, are forced with observed SSTs for the 30°N–30°S domain only, while SSTs and sea ice concentrations outside of the domain are set to climatology. Further information on the model experiments may be found in Deser and Phillips (2009) and on http://www.cesm.ucar.edu/working_groups/Variability/experiments.html.
3 Results
3.1 Linear temperature trends
Linear trends of the temperature anomalies in the four Antarctic-focused datasets (including versions 1 and 2 of Steig et al. (2009)) are compared in Tables 2 and 3 for annual and seasonal means. Table 2 spans the entire period of each record (since 1958 or 1960), while Table 3 covers the period from 1979 to the end of the records (as early as 2002 for the CHAPMAN analysis and as recent as 2009 for the M10 analysis). The results in Table 2 indicate that temperature trends over the last 45–50 years for the Antarctic continent as a whole are in generally good agreement. Positive annual trends are found in all four reconstructed datasets, with an average trend of 0.12°C/decade. The annual trends are significant in the STEIGv1 and the M10 reconstructions. Similarly, the GISTEMP analysis shows an annual average trend of 0.13 ± 0.08°C/decade for the domain 64°S–90°S for 1958–2008. The confidence intervals overlap for all of the data, so there is no significant discrepancy among the reconstructions. While there has been debate about whether continent-averaged trends are meaningful (e.g. Turner et al. 2005), most assessment studies have consistently estimated an annual long-term trend on the order of 0.1°C/decade (e.g. Steig et al. 2009; Monaghan et al. 2008; Chapman and Walsh 2007; Jacka et al. 2004; van den Broeke 2000).
The trends exhibit a distinct seasonality. The trends in summer (DJF) and autumn (MAM) are comparatively small. In contrast, winter (JJA) and spring (SON) trends are uniformly positive and generally larger across the datasets. The winter trend reaches significance at the 90% level in STEIGv1, while the spring trend is significant at the 95% level in M10.
Trends for the EAIS domain largely mirror those for the continent as a whole because it comprises approximately 70% of the Antarctic land area. While no significant seasonal trends are found for EAIS, the positive annual trend is marginally significant in the M10 reconstruction. WAIS has significant positive trends in all seasons according to at least one of the reconstructions. However, the positive spring trend stands out as significant in three of the four datasets. Accordingly, the spring warming evident for all Antarctica largely comes from West Antarctica. All four of the datasets indicate that the spring and annual warming rates are slightly larger for the WA than the WAIS domain, while the winter warming trend is not statistically significant in the WA domain. The average central trend estimate of the four datasets for WAIS is 0.18°C/decade for the annual mean.
It is also interesting to compare the trends of the reconstructions with trends at the in situ stations that are within the Pacific sector, Faraday/Vernadsky and Scott Base. The well documented warming at Faraday/Vernadsky (Turner et al. 2005; King 1994) is significant in all seasons, however warming at Scott Base is only significant in spring. The British Antarctic Survey (http://www.antarctica.ac.uk/met/gjma/) provides a comparable, up-to-date analysis of trends in the READER station data, consistent with our results.
Trends for 1979-present (Table 3) for the WAIS and WA domains show a marked seasonal contrast, with the largest amplitude in spring, the only season when trends are statistically significant. Compared to the full period, trends since 1979 are similar in winter and stronger in spring. Faraday/Vernadsky and Scott Base mirror this change; starting in 1958 the spring trends are about 0.41°C/decade while starting in 1979 the trends are 0.6–0.8°C/decade.
For the All Antarctica and EAIS domains, the seasonality of 1979-present trends is even more distinctive than for the 1958-present trends. All of the datasets show negative trends in autumn and most show negative trends in summer. While these trends are not statistically significant, their consistency among datasets suggests that they are real and relevant for physical interpretations.
With regard to the 1979-present spring trend over WAIS, the 0.30°C/decade trend from the STEIGv2 reconstruction is a lower bound, because STEIGv2 utilized detrended AVHRR data to calibrate the reconstruction. The trend of 0.87°C/decade from the M10 reconstruction provides an upper estimate. For spring the new Byrd record incorporated into the M10 reconstruction has the greatest uncertainty of any season due to gaps in the AWS records that can occur in the late winter and early spring because of instrument failure (A. Monaghan, personal communication, 2010). This source of concern is somewhat mitigated by comparing the AWS-generated Byrd record with a record infilled with passive microwave satellite observations (e.g. Shuman and Stearns 2001; Bromwich et al. 2008); the independent passive microwave record also suggests strong upward trends in spring. Nonetheless, the 0.87°C/decade trend in the M10 record should be considered an upper bound. The large, positive trends at both Faraday and Scott Base lend credibility to the derived reconstructions. Stations in the vicinity of Faraday/Vernadsky and Scott Base, Rothera and McMurdo, respectively, also show large positive trends and thus confirm that the spring warming likely covers a large region, and is not an artifact of individual observational measurements, nor dependent on using the AVHRR data. As a central estimate, the average spring warming trend of the four datasets shown in Table 3 for WAIS since 1979 is 0.54°C/decade.
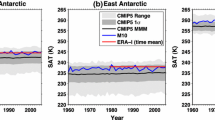
Timeseries of the temperature anomalies in the three Antarctic reconstructions are displayed in Fig. 2, for annual and spring means. These timeseries demonstrate that both the year–year variability and the trends are highly correlated among the datasets. The larger variance of the M10 reconstruction is because the variance is scaled to match that of the ERA-40 reanalysis (Monaghan et al. 2008), while the variance of the STEIGv1 reconstruction contains only the variance explained by the leading three EOFs of the satellite data (about 60%). The interpolation procedure of the CHAPMAN reconstruction reduces the amplitude of the reconstructed temperature anomalies.
Comparing the annual timeseries (Fig. 2), the EAIS and WAIS timeseries are similar from the 1960s through the 1980s, but show differences in the 1990s. Relatively cold years of the early and late 1990s are prominent in the EAIS records. The early 1990s anomaly is weak in the WAIS records, while the late 1990s cold anomaly is absent in the WAIS records. The cold anomalies in the annual mean for the EAIS arise largely from summer and autumn (not shown). Interpreted as a trend, these cold years have been linked to the positive phase of the SAM, which explains much of the cooling in coastal East Antarctica (Marshall, 2007). Cooling in the early 1990s could also be linked with the 1991 Mt. Pinatubo volcanic eruption (Jacka et al. 2004). Chapman and Walsh (2007) discussed a sensitivity of the sign of Antarctic temperature trends to the start and end dates of the analysis. The absence of large negative anomalies in the 1990s for the annual WAIS timeseries implies that the sign of the temperature trend for WAIS is less sensitive to start dates of the analysis than for EAIS and all Antarctica.
Comparing the spring (SON) timeseries (Fig. 2, right panel), the EAIS and WAIS records exhibit a broad agreement on the interannual scale but different trend structures. 1977 stands out as the coldest year of the entire record for both EAIS and WAIS for all of the datasets. Prior to this, persistent warmth occurred from 1970 to 1975, a prominent anomaly that has been noted before (Schwerdtfeger 1976; Mosley-Thompson et al. 1991) and is consistent with positive anomalies of atmospheric mass over the Antarctic (Swanson and Trenberth 1981), and with positive oxygen isotope anomalies in West Antarctic ice cores (Mosley-Thompson et al. 1991). The increase in atmospheric mass over Antarctica from the early 1960s to the early 1970s discussed by Swanson and Trenberth (1981) is physically consistent with the upward temperature trends of the early part of these records. This result is encouraging in light of the difficulty of verifying the reconstructions in the data sparse period before 1979. The more recent upward trend in WAIS temperatures began roughly in the late 1970s.
3.2 Spring temperature and sea ice trends 1979-present
Due to their large amplitude, statistical significance, and lack of discussion in previous work, the spring temperature trends are explored further in the remainder of this study. Figure 3 shows the spatial pattern of spring temperature and sea ice fraction trends in several datasets from 1979 to the most recent available year (varies by dataset), including global analyses that do not exclusively focus on the Antarctic.
Comparison of spring temperature trends in several datasets for 1979-present, as labeled. The top left panel also displays trends in sea ice fraction—note that the scale is reversed relative to the temperature scale; the 1979–2008 climatological 15% ice edge contour for SON is also shown (heavy black line). The open circles on each panel represent the trends at the READER stations. Gray shading indicates missing data or that not enough data were available to calculate a trend—a requirement was imposed that the gridpoint or station record contained at least 20 years of observations to display the trend. In the top left panel, the squares on the continent indicate the trends in the SteigAWS reconstruction
All of the datasets shown in Fig. 3 indicate positive temperature trends over West Antarctica. As discussed above, the magnitudes vary somewhat, ranging from about 0.3°C/decade to greater than 1°C/decade. The M10, GISTEMP, and CHAPMAN trend patterns are quite similar to each other, showing positive trends from Orcadas station near 40°W through West Antarctica to ~135°E. The spatial pattern of the STEIGv2 data is also quite similar, but the trend magnitudes are somewhat lower than M10 across West Antarctica and lower than the station observations at Scott Base and Faraday/Vernadsky. For West Antarctica, STEIGv1 is in good agreement with the other reconstructions, as is the SteigAWS. The only two station records with cooling trends are to the east of the Peninsula, Halley and Neumayer. This (insignificant) cooling is represented as a near-zero or negative trend in the GISTEMP, CHAPMAN, and M10 reconstructions, but not in the STEIGv1, AVHRR, or MSU. The lack of cooling in the MSU over Halley and Neumayer suggests that the negative trend may be confined to the near-surface levels.
Over East Antarctica, most of the reconstructions and the station data are in agreement, showing near-zero trends for coastal East Antarctica and some positive trends inland, around Vostok and the South Pole. The AVHRR data and STEIGv1 show (statistically insignificant) warming over coastal East Antarctica, in disagreement with the station data and the other reconstructions. This suggests that the AVHRR trends over coastal East Antarctica may not be reliable. The AVHRR data also show a patch of negative trends near the South Pole that are not supported by the station data or by any of the reconstructions. Collectively, the datasets show positive temperature trends across West Antarctica, and neutral trends in coastal East Antarctica, consistent with the timeseries discussed above (Fig. 2 and Table 3).
Sea ice concentration, which is independently measured and well observed by passive microwave satellite sensors, gives additional important information on changes in the Antarctic environment. The trends in sea ice concentration, expressed as fractional change per decade are plotted in Fig. 3 with the sign inverted with respect to the sign of the temperature trends. Negative sea ice trends (warm colors) predominate from the vicinity of Orcadas station near 40°W to the eastern Ross Sea at 130°W. Positive sea ice trends (cool colors) predominate from 140°W to 120°E, while trends are small from 120°E to the Greenwich Meridian. The trends are largest in the latitudes near the ice edge where the climatological concentration gradients are largest, and smallest near the inner ice pack where concentrations are typically above 85% (Fig. 1). Examination of sea ice trends in each month of the year shows that the large-scale spatial patterns of sea ice trends are remarkably persistent from month to month (not shown). While the trend magnitudes and northward extent of the anomalies differ by month, the pattern of Ross Sea increase and Amundsen-Bellingshausen Sea decrease is not unique to austral spring, a result consistent with many studies (e.g. Turner et al. 2009; Comiso et al. 2008; Stammerjohn et al. 2008; Jacobs and Comiso 1997).
The positive temperature trends over the WAIS are spatially adjacent to the negative trends in sea ice concentration over the Amundsen and Bellingshausen Seas. Although there has been a positive sea ice trend in the Ross Sea, it is quite distant from the coastline of West Antarctica from 130°W to the dateline, but approaches the coastline of East Antarctica from 130°E to 90°E. The positive sea ice trend near coastal EAIS is adjacent to the continental region that shows neutral or slightly negative temperature trends.
The adjacent and opposing trends in sea ice and air temperature suggest that the two are related. The negative sea ice-temperature relationship is intuitive and has been observed before in the Peninsula region (e.g. Turner et al. 2005; Jacobs and Comiso 1997; King 1994; Weatherly et al. 1991). Several ocean-air-sea ice feedback processes may be operating (Meredith and King 2005; Hanna 1996), though it has been difficult to pin down their relative roles in the observational studies (King 1994; Jacobs and Comiso 1997). Here, we do not address the feedback processes, but instead show that the sea ice trends are consistent with the regional temperature and atmospheric circulation trends, lending confidence to the systematic view of change in the Antarctic.
Over the Southern Ocean to the north of the sea ice edge, the temperature trend patterns are broadly similar among the datasets. Note that the datasets show different quantities; in the sea ice zone the GISTEMP, M10 and CHAPMAN data represent air temperature (though CHAPMAN air temperatures are inferred from SST input data); north of the sea ice edge the M10 and CHAPMAN data represent air temperature while GISTEMP represents SST; MSU represents tropospheric-average temperatures everywhere. For much of the ocean, the trends are nearly zero. Around the Peninsula, warming trends prevail. Some of the datasets show cooling in the South Atlantic from 30°E to 30°W, though this is strongest in the CHAPMAN data that end in 2002. Cooling is also observed in the South Pacific at ~60°S, ~150°W, extending toward the southern tip of South America, especially in the M10 and MSU data.
Jacobs and Comiso (1997) noted the strong sea ice-temperature correlation at Faraday/Vernadsky, and, on the basis of the negative trend in sea ice extent in the Amundsen-Bellingshausen Sea, suggested that the warming trend then observed in the Peninsula might extend westward along the Amundsen Sea coastline. The results above and in Fig. 4 support the Jacobs and Comiso (1997) conjecture. Figure 4 shows the SON timeseries for WA temperature anomalies from M10 compared with sea ice area in the Amundsen-Bellingshausen Sea. The correlation is −0.73, significant at the 95% level, and nearly identical to the correlation for sea ice lagging temperature by 1 month (not shown); sea ice anomalies lagging temperature anomalies by ~1 month typically gives the strongest correlation in the Antarctic (e.g. King 1994; Jacobs and Comiso 1997). Spring stands out as having the largest seasonal correlation of WA temperature anomalies and Amundsen-Bellingshausen sea ice anomalies, as the correlations are much weaker in other seasons (<−0.3 and not significant).
Comparing the reconstructions, the correlation of ABS ice area with the WA temperature timeseries is r = −0.58 (P < 0.05) for STEIGv1, −0.58 (P < 0.05) for STEIGv2, and −0.40 (P < 0.10) for CHAPMAN. Due to the higher covariance of sea ice and WA temperature anomalies in the M10 dataset, we use M10 data to illustrate the rest of the analyses in our paper. Qualitatively similar results to those discussed below can be obtained with the STEIGv1 or STEIGv2 datasets, but the results are stronger with the M10 dataset. Additionally, the M10 dataset provides the longest period of overlap with the sea ice data and with the NCEP2 Reanalysis. While the M10 dataset exhibits a larger spring warming trend on WAIS than the other datasets, the spatial pattern and magnitudes of trends closely match those of the READER station data (Fig. 3) where overlap occurs.
3.3 Forcing of sea ice anomalies
The 1979–2008 trends in the 10-m winds from NCEP2 are displayed in Fig. 5a, together with changes in sea ice concentration and temperature on land from M10. These changes can be compared with the climatology in Fig. 1. Winds can influence sea ice concentration in several ways, including via atmospheric thermal advection, oceanic Ekman currents, and wind-driven dynamic transport (e.g. Holland and Raphael 2006). The wind trends shown in Fig. 5a are qualitatively consistent with a role in forcing the sea ice trends via Ekman transport and atmospheric thermal advection. Specifically, in the 0°W–30°W sector, southerly wind trends advecting cold air equatorward coincide with increased sea ice concentration. Similarly, southerly wind trends occur near the ice edge in the Ross Sea from 150°W to 150°E, where ice concentration has increased. In the Weddell Sea from 30°W to 60°W, northerly wind trends advecting warm air poleward coincide with decreased sea ice concentration. In the ABS the wind trends are northerly to easterly. The easterly wind trends could enhance poleward Ekman transport (e.g. Hall and Visbeck 2002) while the northerly wind trends are consistent with warm air advection over the ice pack. The wind trends in the Eastern Hemisphere are relatively weak. Inspection of wind trends in other reanalysis datasets, including ERA-40 (Uppala et al. 2005), JRA-25 (Onogi et al. 2007), and the National Aeronautics and Space Administration Modern Era Retrospective Analysis for Research and Applications (NASA-MERRA) dataset (Bosilovich et al. 2006), reveals similar overall patterns (not shown).
(a–b) Maps of 30-year (1979–2008) changes in Antarctic continental temperature from M10 (colors on Antarctic land), sea ice fraction (colors over ocean; note the scale is reversed with respect to temperature), and 10-m winds (vectors; omitted south of 75°S.). Stippling indicates where the sea ice or temperature trends are significant at the 95% level. a Wind changes for SON, b wind changes for JAS, overlaid on the same SON sea ice and temperature changes. On the bottom panels (c–d), the SON temperature changes that are linearly congruent with the SON trends in sea ice area for (c) the Bellingshausen Sea and (d) the ABS. Stippling indicates where the sea ice-temperature regression coefficients with detrended timeseries are significant at the 95% level
Some previous analyses concluded that sea ice has a maximum response to sea level pressure and wind forcing at 1–3 month lag (e.g. Holland and Raphael 2006; Yuan and Li 2008), though sea ice-SLP correlations are still relatively high at zero-lag (Yuan and Li 2008). In Fig. 5b, the July–August–September (JAS) winds are overlaid on the same SON sea ice and continental air temperature trends. The JAS and SON wind trends are similar in the Weddell and ABS, but the cyclonic anomaly in the vicinity of 150°W in the Ross Sea is much weaker in JAS. Hence, the JAS wind vectors overlying the SON ice anomaly in the Ross Sea are polewards, inconsistent with the SON trends. However, stronger westerlies to the north of the Ross Sea ice edge in both seasons could contribute to equatorward Ekman transport (Hall and Visbeck 2002).
The terrestrial temperature change that is linearly congruent with the ABS and Bellingshausen sea ice trends are displayed in Fig. 5c, d. This illustrates that up to 50%, or ~1.5°C of the ~3° 30-year change in the M10 data is linearly congruent with the decrease in the ABS sea ice area. Considering the Bellingshausen Sea separately (Fig. 5c) illustrates that up to about 80%, or 1.2°C of the 1.5°C spring (central) Peninsula warming and a portion (0.6°C to 0.9°C, or 20–30%) of the inland WAIS warming is consistent with the Bellingshausen Sea sea ice changes alone. However, the ABS sea ice area shows a larger area of statistically significant temperature regression coefficients than the Bellingshausen Sea sea ice. Some cooling on the EAIS also appears to be connected with the ABS sea ice trends, likely through organized patterns of atmospheric circulation changes. Note that we computed sea ice–temperature regression coefficients with detrended data and then multiplied these by the trend of the sea ice area to obtain the congruent temperature change. This calculation serves to support the idea that sea ice trends may be contributing to temperature trends and/or vice versa, but does not prove a chain of causality. In fact, it suggests that other, large-scale processes should be considered.
3.4 Relationship of temperature and sea ice anomalies with trends in the SH atmospheric circulation
It is well established that large-scale modes of the extratropical SH atmospheric circulation have strong impacts on Antarctic sea ice (e.g. Yuan and Li 2008; Stammerjohn et al. 2008; Holland and Raphael 2006; Liu et al. 2004; Kwok and Comiso 2002; Yuan and Martinson 2000) and on continental temperature anomalies (e.g. Marshall 2007; van den Broeke and van Lipzig 2004; Schneider et al. 2004; Kwok and Comiso 2002; Turner 2004; Bromwich et al. 2004; Thompson and Solomon 2002). The leading mode is typically referred to as the Southern Annular Mode (SAM), though sometimes referred to as the Antarctic Oscillation. The second mode is usually termed the Pacific-South American (PSA or PSA-1) pattern because it resembles its northern counterpart, the Pacific-North American (PNA) pattern, and like the PNA, it is known to respond significantly to ENSO forcing (e.g. Turner 2004). The third mode is often referred to as PSA-2 (e.g. Mo and Higgins 1998; Mo 2000). The association of PSA-2 with tropical variability is less clear than PSA-1. According to Mo (2000), PSA-2 is related to the quasi-biennial component of ENSO variability. However, other authors have described PSA-1 and PSA-2 as geographically fixed oscillatory patterns that are only excited by ENSO variability in the austral spring (Robertson and Mechoso 2003). The amplification of the SH ENSO signature, which largely projects on PSA-1, in austral spring compared with the other seasons was discussed by Jin and Kirtman (2009) and shown to reflect the seasonality of the SH atmosphere, rather than the seasonality of ENSO forcing.
To best capture the changes in atmospheric circulation associated with sea ice anomalies in the ABS and temperature anomalies on the WAIS, we calculate the leading three EOFs of area-weighted seasonal mean anomalies of 850 hPa geopotential height (Z850) for the domain 30°S–75°S and 180°W–0°W from the NCEP2 data using the covariance matrix. The results are illustrated as regression maps of the leading detrended Z850 principal components (PCs) timeseries with detrended fields of Z850, Antarctic continental temperature, and SH sea ice anomalies (Fig. 6a–c). Note that we used the trended seasonal mean data for the EOF analysis so that we could calculate trends in Antarctic temperature and sea ice that are linearly congruent with trends in the modes of atmospheric circulation. The patterns in Fig. 6a–c are similar using the full range of longitudes for the EOF analysis rather than the Western Hemisphere alone, but more of the variance in the region of interest and trends (Fig. 6d–f) are captured using the smaller domain.
Top row (a–c): Regressions of the leading detrended Z850 PC timeseries with anomalies in continental Antarctic temperature from M10 (colors on Antarctic land), sea ice concentration (colors over ocean; (note the sea ice colorscale is reversed with respect to the temperature colorscale), and geopotential height (contours). The temperature units are °C per standard deviation of the PC; the sea ice units are percent/−10 per standard deviation of the PC; the Z850 contours are meters per standard deviation of the PC, and the contour spacing is 10 m, with positive values solid lines and negative values dashed lines. Bottom row (d–f): 30-year (1979–2008) trends in temperature, sea ice, and Z850 linearly congruent with trends in the PCs. In (d–f) the temperature units are °C per standard deviation of the PC per 30 years; the sea ice units are percent/−10 per standard deviation of the PC per 30 years; the Z850 contours are meters per standard deviation of the PC per 30 years, and the contour spacing is 10 m, with positive values solid lines and negative values dashed lines
For consistency with the idea that wind forcing precedes sea ice concentration anomalies by ~2 months (Yuan and Li 2008), we also computed the PCs of Z850 for JAS and regressed these upon SON Antarctic sea ice and continental temperature anomalies (not shown). The resulting regression coefficients are much weaker, and almost none of the sea ice and WAIS temperature trends in SON are congruent with circulation trends in JAS. For SON, similar regression patterns are obtained if different atmospheric levels (e.g. Z1000, Z500) are used instead of Z850, but Z850 was found to have the greatest correspondence with ABS sea ice anomalies (not shown).
The first mode resembles the SAM and explains 42% of the variance of the Z850 anomalies, and has a strong influence on Antarctic temperature and sea ice anomalies (Fig. 6a). In the Western Hemisphere, on the Peninsula and over the sea ice, the circulation changes associated with the SAM are consistent with thermal advection by the anomalous winds. Over the polar plateau and coastal escarpment of East Antarctica, where regression coefficients are 0.5°C to 0.9°C (and are even higher in DJF and MAM, not shown, but see Marshall (2007)) another explanation is necessary. Since the strong association between the SAM and East Antarctic climate is not often clearly addressed in the literature, we discuss it here in conceptual terms. Climatologically, a surface high is present over the ice sheet, while to the north of the continent at ~60°S lies the circumpolar trough. These features are coupled through a thermally direct circulation that represents the mean meridional circulation at the high latitudes (Parish and Bromwich 2007). This circulation and its poleward heat transport must exist to balance the surface energy budget, especially the strong longwave cooling term (e.g. Warren 1996). Near the southern limit of the circumpolar trough at the latitude of ~65°S, rising motion occurs and turns polewards aloft (Parish and Bromwich 2007). Slow subsidence occurs over the continent and explains the surface high. The surface energy budget is balanced through turbulent mixing at the boundary layer and sensible heat flux (e.g. Warren 1996; van den Broeke et al. 2006). The surface katabatic wind regime, directed equatorwards and down the Antarctic coastal escarpment, closes the lower branch of the circulation (Parish and Bromwich 2007).
By definition, a positive phase of the SAM implies lower than normal surface pressure over the Antarctic continent and reduced mean meridional circulation, and negative SAM implies the opposite. This basic explanation of reduced meridional heat transport associated with positive SAM is consistent with the modeling study of van den Broeke and van Lipzig (2004). Over the coastal escarpment, the regression coefficients of temperature anomalies with the SAM are an indication that the SAM is tied with the surface energy balance and modulation of the thermally direct circulation as described by Parish and Bromwich (2007); the katabatic winds mix sensible heat towards the surface to balance longwave cooling (van den Broeke et al. 2006). Should positive SAM perturb this balance, lower than normal surface temperatures would result. Reduced subsidence over the continent leads to the anomalous surface low pressure. Ozone depletion can perturb the meridional circulation both by modifying the vertical temperature gradient that exists above the continent as well as the large-scale meridional temperature gradient.
The second and third modes are distinct from the SAM. They explain 19 and 11% of the variance, respectively. The third mode is similar to PSA-1 of Mo (2000), which is strongly correlated with the SOI and with SSTs in the tropical Pacific in an ENSO-like pattern. The tropical SST correlation with PSA-1 maximizes in austral spring (Mo 2000). The second mode, similar to Mo’s PSA-2, exhibits a zonal wavenumber-3 structure in the SH mid-high latitudes. Both PSA-like modes are associated with significant anomalies of Antarctic sea ice concentration and temperature (Fig. 6b–c).
3.5 Trends in the circulation and congruent trends in Antarctic temperatures and sea ice
How do the modes of atmospheric variability relate to the trends, and why are the trends maximized in spring? The temperature, sea ice, and Z850 trends that are linearly congruent with trends in the first three PCs of Z850 are shown in Fig. 6d–f. This figure indicates that the observed trends are most influenced by trends in the third PC. The trend in PC3 is congruent with about 1°C, or about a third of the warming in some areas of the WAIS, 15–20% reduction in sea ice concentration in the Bellingshausen Sea, and a 9–14% increase in sea ice concentration in the Ross Sea. The trend in PC2 is congruent with an additional 2–14% decrease in sea ice concentration in the Amundsen Sea and a relatively small amount of warming (~0.5°C) in WA. The trends congruent with PC1 are comparatively weak and insignificant. The lack of a significant trend associated with PC1 is consistent with the lack of a trend in the SAM in austral spring (Marshall 2007). However, the SAM has undergone a significantly positive trend in summer (DJF) and autumn (MAM) and a weaker positive trend in winter (Marshall 2007). Thus, the seasonal characteristics of the SAM trends are consistent with the lack of significant warming trends in WA and EAIS in DJF, MAM and JJA, while circulation trends not associated with the SAM must explain the warming of WA in SON.
Figure 7a displays the observed trends in temperature, sea ice and geopotential height. By geostrophic balance, the trends in Z850 are qualitatively consistent with the near-surface wind trends shown in Fig. 5a. Positive height trends are evident over the south Atlantic while negative trends are evident in the South Pacific, contrasted with positive height trends in the subtropical Pacific. Broadly, the Z850 trend pattern of a north–south dipole over the South Pacific and an east–west dipole in the high southern latitudes with a node near the Peninsula, is reminiscent of the PSA-1 pattern, consistent with the congruency analysis for the third Z850 PC above.
a 30-year (1979–2008) trends in temperature from M10 (colors on Antarctic land), sea ice concentration (colors over ocean; note the sea ice colorscale is reversed with respect to the temperature colorscale), and Z850 (contours). The temperature units are °C per 30 years; the sea ice units are percent/−10 per 30 years; the Z850 contours are meters per 30 years, and the contour spacing is 10 m, with positive values solid lines and negative values dashed lines. b The trends that are explained by trends congruent with the second and third modes of atmospheric circulation (sum of Fig. 6e–f). c Residual trends, not explained by the two modes of atmospheric circulation
While the observed circulation trends project most strongly onto the third Z850 PC, the second Z850 PC is congruent with larger circulation trends in the western Amundsen and eastern Ross Sea (Fig. 6e). The observed trend pattern over the South Pacific (Fig. 7a) is therefore best captured by a combination of the second and third modes of Z850. Figure 7b displays the total trends in temperature, sea ice and geopotential height that are explained by these two modes and the residual, unexplained trends are shown in Fig. 7c. At least 30 m of the maximum decrease of 50 m in the cyclonic pattern centered at 150°W, 60°S is explained by the two modes combined. Furthermore, virtually all of the negative trends in ice concentration in the Amundsen Sea and a third or more of the negative sea ice trends in the Bellingshausen Sea are explained, along with a third or more of the positive sea ice trends in the Ross Sea. On land, about 20–40% of the warming across the WA domain and all of the cooling in the 0°W–30°W sector is explained. The pattern of temperature trends associated with the two circulation modes (Fig. 7b) closely resembles the pattern of temperature trends associated with trend in the sea area in the ABS (Fig. 5d). This quantitative result confirms our qualitative description of the near-surface wind trends (Sect. 3) and their likely forcing of the sea ice trends.
Comparing the two figures (5d and 7b), it is apparent that the sea ice area explains about a third more of the temperature increases than does the atmospheric circulation directly. However, the covariance between the temperature and the circulation fields is greater if regression coefficients are calculated with the original rather than the detrended timeseries. When the congruency analysis is done with trended data (Fig. 8a), the spatial patterns are very similar to the detrended case (Fig. 7b), suggesting that the trends do not result in spurious regression values, but the explained trend is greater. The patterns congruent with the atmospheric circulation (Fig. 8a) are remarkably similar to the patterns associated with the ABS sea ice area (Fig. 8b). The region over which the circulation (Fig. 8a) and sea ice (Fig. 8b) regression values are statistically significant at 95% confidence closely matches the region of statistically significant temperature trends (Fig. 5a). This result strongly supports our interpretation of the low-level wind trends (Fig. 5a) and their role in driving the anomalies of sea ice concentration in the ABS and of temperature on the WAIS.
30-year (1979–2008) changes in temperature from M10 (colors on Antarctic land), sea ice concentration (colors over ocean; note the sea ice colorscale is reversed with respect to the temperature colorscale), and Z850 (contours) that are congruent with (a) The second and third modes of atmospheric circulation and b The sea ice area in the Amundsen-Bellingshausen Sea. In both panels, the temperature units are °C per 30 years; the sea ice units are percent/−10 per 30 years; the Z850 contours are meters per 30 years, and the contour spacing is 10 m, with positive values solid lines and negative values dashed lines. In this analysis, trends were left in the timeseries to calculate the regression coefficients
The consistency of the sea ice trends with the circulation trends, and in turn of the temperature trends with the sea ice trends, suggests that the circulation trends are realistic, and not an artifact of the reanalysis. Although trends in the reanalysis can be problematic at high latitudes, the existence of positive height trends over the continent in spring (Fig. 9a) is confirmed by the results of Neff et al. (2008). Using radiosonde data from READER, they found both a seasonal cycle and a geographical asymmetry to the height trends. Seasonally, at all of the seven coastal and interior station records examined by Neff et al. (2008), positive trends maximized in September, while May showed maximum negative trends. October and November also showed positive trends. Geographically, trends in Z500 were greatest at the South Pole and McMurdo stations and smallest over coastal East Antarctica. Neff et al. (2008) did not have data to analyze for West Antarctica or the Peninsula. Although Neff et al. (2008) analyzed the Z500 level, trend patterns at Z850 and Z500 in the NCEP2 data are quite similar (not shown).
a Trends (1979–2008) in SON Z850 from NCEP2 (black contours; negative dashed and positive solid; interval of 6 m/decade); surface temperature from GISTEMP (background colorscale in units of °C/decade; air temperature in the polar sea ice zones and SST elsewhere); and GPCP precipitation (positive green contours, negative red contours, contoured at −0.7, −0.3, −0.1, 0.1, 0.3, and 0.7 mm/day/decade, shown only for 45°S–45°N). The purple box in the central southern tropical Pacific outlines the region used for the SST timeseries (taken from HadSST2) discussed in the text and displayed in Fig. 10. b Trends surface temperature from the GOGA CAM3 simulations (background colorscale; air temperature over sea ice and SST elsewhere) along with the Z850 trend produced by the model simulations (black contours; negative dashed and positive solid; interval of 3 m/decade) and the simulated convective precipitation trends (positive green contours, negative red contours, contoured at −0.7, −0.3, −0.1, 0.1, 0.3, and 0.7 mm/day/decade, shown only for 45°S–45°N. (c) As in (b) but for the TOGA CAM3 simulations. In both GOGA and TOGA simulations, the surface temperature over sea ice can respond to both prescribed sea ice and simulated atmospheric circulation changes, which explains differences with observations
The pattern of small height trends over coastal East Antarctica and larger trends to the west and inland at South Pole found by Neff et al. (2008), is broadly consistent with the pattern shown in the reanalysis. Surface pressure trends from the READER dataset are also predominantly positive in spring (not shown), consistent with the SAM trends calculated by Marshall (2007). Although it does not cover the South Pole, the warming pattern evident in the MSU data (Fig. 3) is consistent increased atmospheric thickness from the surface to the mid troposphere and rising geopotential height over the continent and in the Weddell Sea sector. Likewise, the cooling in the South Pacific Sector over the Ross Sea Ice edge and to the north of it (Fig. 3) corresponds with the northern side of the negative geopotential height trend evident in NCEP2 that implies anomalous equatorward advection of cold air.
The analysis of the sea ice trends congruent with the atmospheric circulation is not without limitations. The two PSA modes together do not account for the decrease of sea ice in the 30°W–60°W sector. While it is tempting to attribute the unexplained sea ice trends to other factors such as increased upwelling of relatively warm circumpolar deepwater (Thoma et al. 2008), an intensification of the hydrological cycle and increased ocean stratification (Liu and Curry 2010), or eastward propagation of sea ice anomalies (Holland et al. 2005), the observed northerly wind trends (Fig. 5a) are qualitatively consistent with the decrease in sea ice in the 30°W–60°W sector. A positive phase of the SAM, contributing to stronger westerlies in this sector (Fig. 6a) could also explain the sea ice trend. The SAM has not had a significant trend in SON, but the sea ice and SST anomalies associated with the positive SAM the rest of the year could persist. Thus, at least for the spring season, it seems unnecessary to invoke processes other than the atmospheric circulation to explain trends in Antarctic sea ice.
Liu et al. (2004) conducted a congruency analysis similar in some respects to ours, but had difficulty in explaining Antarctic sea ice trends in terms of changes in the SAM and ENSO. Our method is more successful, at least for spring. This is likely because we maximized the covariance between the sea ice field and the atmospheric circulation by restricting our time averaging to the seasonal mean and restricting our spatial domain to 0°–180°W and 30°–75°S. Inevitably, indices calculated from local data will explain more local variance than those based on remote data. Their SAM index, while based on mid-high latitude Z850 data, projects more weakly onto sea ice anomalies in the South Pacific sector than do the PSA modes (Yuan and Li 2008). The Niño3 index used by Liu et al. (2004) only indirectly relates to the Antarctic sea ice field. Moreover, the Niño3 index does not capture the low frequency, decadal scale variations of tropical climate that could influence the extratropics (Deser et al. 2004).
3.6 Relationship of high-latitude circulation trends with global observed SST trends and model results
While we have shown a close relationship between trends in Antarctic temperatures, sea ice, and the high-latitude atmospheric circulation in the austral spring, the question remains how these high-latitude trends fit into the global context of SST and atmospheric circulation changes. Given that the high-latitude trends are closely associated with the two PSA modes, and that these modes have been linked with ENSO variability (e.g. Mo 2000) and with tropical deep convection (Mo and Higgins 1998), it is natural to hypothesize that the high-latitude trends may be driven by changes in low-latitude SSTs. Additionally, SST is a more likely driver than either trends in the atmospheric concentrations of greenhouse gasses or stratospheric ozone depletion, which project most strongly onto to the SAM, not onto the PSA modes (e.g. Arblaster and Meehl 2006). Moreover, due to the seasonality of the SH atmosphere, the maximum high-latitude response to ENSO forcing is observed in the austral spring (Jin and Kirtman 2009); it is reasonable to expect that the seasonality of the strong tropical-high latitude linkage applies to the lower frequency as well as the interannual ENSO timescale.
Observed 1979–2008 trends in global surface temperatures, Z850 and low-latitude precipitation are shown in Fig. 9a, and the simulated trends in Z850 and precipitation from the GOGA and TOGA ensemble means are shown in Fig. 9b, c, respectively. In GOGA, the simulated Z850 trend pattern in SON broadly resembles the pattern observed in the NCEP2 data. Specifically, the model is successful in reproducing the decrease in heights over the high-latitude South Pacific and increases in heights over the southern subtropical Pacific and high-latitude South Atlantic. There are also some differences between the observed and modeled circulation trends, including a westward shift of the south Pacific center of action and a lack of negative trends over the Antarctic continent in nature. The tropical Pacific near the dateline is an important region for the origination of Rossby wave-trains forced by changes in atmospheric deep convection that result in teleconnections to the high-latitude South Pacific and Atlantic such as occur during ENSO events (e.g. Bromwich et al. 2004; Turner 2004). In terms of precipitation trends in this region, a proxy for anomalous deep convection, the observations indicate a general increase within the South Pacific Convergence Zone (SPCZ) (trends of up to 0.6 mm/day/decade) and a decrease to the east of the SPCZ. This precipitation pattern is consistent with the underlying SST trend pattern, which exhibits an increase in the western equatorial Pacific extending southeastward into the subtropics. The SST trends are near-zero directly along the equator in the central Pacific and negative in the eastern Pacific. The model, forced with observed SSTs, generally reproduces the observed pattern of precipitation trends in the central and western tropical Pacific, with increases in convective precipitation of up to 0.8 mm/day/decade.
The TOGA ensemble produces very similar tropical precipitation trends as GOGA. The largest high-latitude geopotential height trend is correctly located over the South Pacific sector. However, the high-latitude circulation pattern exhibits a stronger zonal symmetry and generally weaker magnitude than in GOGA or in observations. One reason for the differences between TOGA and GOGA may be the differences in simulated rainfall at the southern edge of the tropics in the 25°–30°S band. Specifically, both observations and GOGA indicate increased precipitation to the northeast of New Zealand extending to 30°S. The TOGA experiment may suppress this precipitation trend because the prescribed SSTs are damped in the 20°–30°S band (Deser and Phillips 2009).
Regardless of the exact reasons for differences in the TOGA and GOGA experiments, the model results support the notion that SSTs in the tropics to subtropics have played a role in forcing the atmospheric circulation trends over the SH in austral spring. Additional diagnostics beyond the scope of this study will be needed to isolate the mechanisms linking the prescribed SST trends to the simulated high-latitude circulation trends. Nonetheless, the observed and simulated low-latitude precipitation trends, together with observations and theory linking the PSA patterns to Rossby wave propagation (e.g. Mo and Higgins 1998; Jin and Kirtman 2009), qualitatively suggest that the increased occurrence or strengthening of Rossby wave propagation has contributed to the PSA-like circulation trends in the SH high latitudes.
The SST trend pattern coincident with the Z850 trend (Fig. 9a) resembles the SST correlation pattern associated with PSA-1 (e.g. Mo 2000). To further explore the role of remote SST trends in the observed trends in the high Southern latitudes, we averaged SSTs from the HadSST2 dataset over the central southern tropical Pacific region where correlations with the PC timeseries corresponding to PSA-1 are the highest, the SST trends are among the largest in the SH, and the precipitation trend is positive (purple box in Fig. 9a). This SST timeseries is displayed in Fig. 10 and compared with the WAIS temperature record from M10 and the in situ temperature record from Faraday/Vernadsky. Table 4 shows the correlations among the timeseries of WAIS temperature, ABS sea ice area, Faraday/Vernadsky temperature, tropical SST, the third PC of Z850, and the combined second and third PCs of Z850. The WAIS temperature timeseries is significantly correlated with all of the other timeseries. Interestingly, WAIS, Faraday/Verdnadsky, and the SST timeseries have all had larger trends since 1979 than for the full period. The third PC of Z850, only available since 1979, is significantly correlated with the SST timeseries. This is again suggestive that SSTs have played a role in forcing high-latitude SH climate trends. Essentially, the correlations of the observational data and the model results are consistent with the hypothesis that increasing low-latitude SSTs have forced anomalous deep convection and rainfall, in turn forcing Rossby wave-trains to the South Pacific. As we have shown, the anomalous atmospheric circulation in the South Pacific largely explains the sea ice and air temperature trends in the Pacific sector of the Antarctic.
Timeseries of WAIS temperature anomalies compared with Faraday temperature anomalies and SST anomalies in the region outlined in Fig. 9a
Given that the past 30–50 years is a relatively short period for evaluating long-term trends, the SST trends themselves could be viewed as a manifestation of large-scale modes of multidecadal Pacific variability (e.g. Zhang et al. 1997; Deser et al. 2004) or as part of the century scale positive SST trends associated with climate change (e.g. Deser et al. 2010); it is likely that both multidecadal climate variability and climate change have contributed to the SST trend pattern evident in Fig. 9 and used to force the model. In the Antarctic, it is also important to recognize that interannual to decadal-scale variability in circulation, sea ice and temperature is quite large, so the pattern of strong West Antarctic warming may not necessarily continue in concert with the global warming trend.
4 Summary and discussion
We have presented three main groups of results. First, the consistency of Antarctic temperature trends among several datasets was assessed, including their seasonal and spatial characteristics. Second, the significant temperature trends in spring were discussed in the context of trends in other observed variables, including sea ice concentration and the atmospheric circulation. Third, we formulated a hypothesis concerning low-latitude SST trends and their influence on Rossby wave propagation as a driving mechanism of the high-latitude circulation trends and provided preliminary evidence in support of this hypothesis.
We first presented a survey of trends since ~1958 and 1979 in several Antarctic temperature datasets, including statistical reconstructions and selected in situ station data. Although there are large variances about the trends, the datasets are consistent in showing a ~50-year annual warming trend of roughly 0.1°C/decade. That the aggregate trends are in good agreement is not surprising given that the reconstructions rely on largely similar underlying sets of READER station records. More interesting are the trends’ seasonal and regional characteristics. Since 1958, West Antarctica has warmed more than East Antarctica, and warming has been greatest in spring. There are more pronounced contrasts since 1979: autumn and, to a lesser extent, summer have predominantly negative trends in East Antarctica, while spring has large, statistically significant warming trends in West Antarctica. Although strong winter warming in the Peninsula region (Turner et al. 2005) and over West Antarctica has been a focus of other studies (Steig et al. 2009; Ding et al. 2010), we found that winter trends in West Antarctica have not been statistically since 1979 (Table 3), though they are significant at Faraday/Vernadsky. Large and statistically significant winter warming trends in the Peninsula, and insignificant but positive winter trends in West Antarctica were reported by O’Donnell et al. (2010) for 1958–2006. While showing more cooling over Marie Byrd Land and the Ross Ice Shelf in the austral autumn and winter than Steig et al. (2009), the O’Donnell et al. (2010) reconstruction shows negligible differences for austral spring, with positive spring temperature trends in West Antarctica twice the magnitude of any other season. Thus, the spring warming trend of West Antarctica is a robust result, evident across a wide range of datasets. The seasonal and regional characteristics of the Antarctic temperature datasets make them useful for interpreting the physical mechanisms that drive Antarctic climate variability, and for informing future interpretations and model evaluations of Antarctic climate change.
We focused on the large spring warming trend since 1979 across West Antarctica that is evident in nearly all of the temperature datasets, including the in situ records at Scott Base and Faraday/Vernadsky. While we have not evaluated all of the feedback mechanisms and internal and external forcing factors involved, we have shown evidence that the West Antarctic warming is consistent with the regional decline of sea ice in the ABS and with the atmospheric circulation trends over the Southern Oceans. For example, West Antarctic temperature anomalies, excluding the Peninsula, are correlated with sea ice area of the ABS at −0.73, and the trend in sea ice area is linearly congruent with at least half of the warming of the WAIS and Antarctic Peninsula. Further research will be needed to characterize the physical mechanisms responsible for this correlation, and why it appears to reach a maximum in spring. Our results extend previous work, which has linked the winter warming of the Peninsula region, particularly its western side, to negative trends in sea ice concentration and extent in the Bellingshausen Sea (Turner et al. 2005; Meredith and King 2005; Jacobs and Comiso 1997; King 1994). Sea ice-temperature relationships are complex (e.g. Hanna 1996), and none of the studies have provided clear explanations of the chain of causality.
While other studies have had limited success in quantitatively explaining Antarctic sea ice trends in terms of the atmospheric circulation (Liu et al. 2004; Stammerjohn et al. 2008), our congruency analysis of sea ice trends with the atmospheric circulation (Figs. 7b, 8a) explains nearly all of the negative sea ice trend in the Amundsen Sea and a significant portion of the negative trends in the Bellingshausen Sea and positive trends in the Ross Sea. As a consistency check, we regressed the timeseries of Amundsen-Bellingshausen sea ice area onto the circulation and temperature data (Fig. 8b), and found remarkably similar spatial patterns to the regression of the combined second and third modes of the atmospheric circulation on sea ice and temperature fields (Fig. 8a). This suggests that the atmospheric circulation trends have influenced both the sea ice concentration and the temperature trends in the Pacific sector of the Antarctic. Importantly, the region of temperature trends explained by trends in sea ice and the atmospheric circulation is the region of trends that are statistically significant. As discussed above, there is a possible role for sea ice positively reinforcing the temperature trends. This idea is partially supported by the result that the ABS sea ice area timeseries explains somewhat more temperature change over West Antarctica than do the PCs of geopotential height.
It is possible that other processes have contributed to Antarctic sea ice trends. Most studies of sea ice trends have shown that the negative trends in the ABS and the opposite trends in the Ross Sea, are persistent year-round (e.g. Turner et al. 2009; Comiso and Nishio 2008; Cavaleri and Parkinson 2008; Stammerjohn et al. 2008). Some authors have assessed how anomalies in one season could reappear in the next or even a year later (Gloersen and White 2001; Stammerjohn et al. 2008), while others have focused on the eastward propagation of sea ice anomalies (e.g. White and Peterson 1996). Such persistence mechanisms suggest that atmospheric circulation anomalies for a given season may not fully explain the pattern of sea ice anomalies within that season. This is important in that the atmospheric circulation trends over the Antarctic vary substantially by season, with summer and autumn exhibiting decreases in sea level pressure over the circumpolar trough and over the continent. By contrast, spring has weakly positive pressure trends over the continent and strong zonal asymmetry in the Southern Ocean. While our congruency analysis can explain the spatial pattern of positive sea ice trends in the Ross Sea and negative sea ice trends in the Amundsen-Bellingshausen Seas, it does not capture the negative trends in the Weddell Sea.
We showed that it is the combination of the second and third PCs of Z850 data in the high-latitude SH that best capture the trend in Z850 and best explain the trends in sea ice and temperature. The two spatial patterns associated with these PCs resemble the PSA-2 and PSA-1 patterns of Mo (2000), respectively. As PSA-1 has been clearly linked with tropical variability on a range of timescales, we explored evidence that low-latitude SSTs may have played a role. The broad pattern of SST trends resembles the pattern of SST anomalies associated with the PSA-1 (Fig. 9a). SST trends are most significantly positive in the central to western part of the southern tropical Pacific, where positive correlations with the PSA-1 pattern are the highest. On average, SSTs in this region have a strong positive correlation with temperature anomalies at Faraday station, via a PSA-like teleconnection. From our EOF analysis of Z850, the third PC, which most closely resembles PSA-1, is significantly correlated with the SST anomalies (Table 4).
Regarding model results, the GOGA ensemble, forced with observed SSTs and sea ice concentration, was able to reproduce the wave-like, PSA trend pattern, albeit the center of action was too far to the east in the South Pacific compared with observations. The TOGA ensemble correctly placed the maximum high-latitude circulation trend in the South Pacific sector, but overall simulated too zonally symmetric of a response compared with observations. We suggest that these differences are due to differences in the prescribed SST field in the two sets of experiments and the corresponding responses of deep convection. In particular, in the region that we highlighted above, GOGA produced a stronger rainfall response. Taken together, these results suggest that SST trends extending into the subtropics may be important for influencing circulation trends in the SH high latitudes. The observational and model results broadly support our hypothesis, but suggest that further work is needed to diagnose the causes of the high-latitude circulation trends in models and observations.
Both ensembles exhibit geopotential height trends that are too negative over the continent. The observed positive height trends over the continent may be indicative of a thermal response to greenhouse gas increases (Neff et al. 2008), counteracting the negative height trends associated with ozone depletion and the dynamical response to greenhouse gas increases (Arblaster and Meehl 2006). Recent changes in the location of maximum spring stratospheric ozone depletion (Evtushevsky et al. 2008) may also be contributing to the negative geopotential height trends in the South Pacific sector and to the east–west asymmetry of Antarctic climate change.
In summary, we showed that the spring temperature anomalies over the WAIS are significantly correlated with sea ice in the ABS, with temperature anomalies at Faraday/Vernadsky, with geopotential height anomalies in the South Pacific, and with SSTs in the southern tropical western Pacific (Table 4). Trends in all of these data are in the direction that would be expected based on studies of the interannual variability in detrended datasets. Results from formal observational data assimilation into a numerical climate model of intermediate complexity are qualitatively in agreement with ours (Goosse et al. 2009). We note however that we have not separated the relative roles of multidecadal variability and externally forced climate change, nor fully discriminated the relative roles of tropical SSTs and extratropical SSTs and sea ice in explaining the circulation trends at high Southern latitudes.
As the spring warming over west Antarctica represents the only significant trend in the interior of Antarctica (excluding Peninsula) for 1979-present, it deserves consideration in studies that seek to understand and model Antarctic climate change. We note that our interpretation that SSTs have played a role in forcing Antarctic climate change is not necessarily at odds with interpretations that focus on the role of stratospheric ozone depletion (e.g. Thompson and Solomon 2002; Perlwitz et al. 2008; Son et al. 2009). Our assessment underscores that temperatures across East Antarctica have not changed significantly, and have even cooled slightly in austral summer and autumn (though no significantly so) since 1979. This observation is very consistent with the seasonality of the SAM trends and their relationships with East Antarctic temperatures (Marshall 2007), as well as with the expected seasonality of the response to stratospheric ozone depletion and the period since 1979 when it has been a significant forcing (e.g. Thompson and Solomon, 2002; Arblaster and Meehl, 2006).
Fogt et al. (2009) addressed the role of ozone depletion in SAM trends by using coupled model output from Twentieth Century runs compared with a long-term, seasonally resolved reconstruction of the SAM index. They argued that the summer SAM trend is consistent with ozone depletion, while the autumn trend may be due to natural variability. Neff et al. (2008) showed that even when the ozone signal is strongest at the surface in summer, the response is highly asymmetric about the continent. Li et al. (2010) found, based on model results, that Indian Ocean warming has partially offset the trend in the SAM caused by ozone depletion. While the projected gradual recovery of the ozone hole is likely to be an important driver of 21st Century Antarctic climate change in general (e.g. Perlwitz et al. 2008; Son et al. 2009), regional predictions of West Antarctic climate change will need to take into account low-latitude SST and regional sea ice changes. Our results point to the need for future observational and modeling studies to focus on the regional and seasonal characteristics of Antarctic climate change, the regional response to ozone depletion, the influence of tropical variability and climate change on Antarctic climate, and on the mechanisms that link sea ice and air temperature in Antarctica.
References
Adler RF, Huffman GJ, Chang A, Ferraro R, Xie PP, Janowiak J, Rudolf B, Schneider U, Curtis S, Bolvin D, Gruber A, Susskind J, Arkin P, Nelkin E (2003) The version-2 global precipitation climatology project (GPCP) monthly precipitation analysis (1979-present). J Hydrometeorol 4:1147–1167
Arblaster JM, Meehl GA (2006) Contributions of external forcings to southern annular mode trends. J Clim 19:2896–2905
Barrett BE, Nicholls KW, Murray T, Smith AM, Vaughan DG (2009) Rapid recent warming on Rutford Ice Stream, West Antarctica, from borehole thermometry. Geophys Res Lett 36:L02708. doi:10.1029/2008GL036369
Bosilovich MG, Schubert SD, Rienecker M, Todling R, Suarez M, Bacmeister J, Gelaro R, Kim GK, Stajiner I, Chen J (2006) NASA’s modern era retrospective-analysis for research and applications (MERRA). US CLIVAR Variations 4:5–8
Brohan P, Kennedy JJ, Harris I, Tett SFB, Jones PD (2006) Uncertainty estimates in regional, global observed temperature changes: a new data set from 1850. J Geophys Res Atmos 111:D12106. doi:10.1029/2005JD006548
Bromwich DH, Wang S (2008) A review of the temporal and spatial variability of Arctic and Antarctic atmospheric circulation based upon ERA-40. Dyn Atmos Oceans 44:213–243
Bromwich DH, Monaghan AJ, Guo ZC (2004) Modeling the ENSO modulation of Antarctic climate in the late 1990s with the polar MM5. J Clim 17:109–132
Bromwich DH, Fogt RL, Hodges KI, Walsh JE (2007) A tropospheric assessment of the ERA-40, NCEP, and JRA-25 global reanalyses in the Polar Regions. J Geophys Res Atmos 112:D10111. doi:10.1029/2006JD007859
Bromwich DH, Monaghan AJ, Colwell SR (2008) Surface temperature and mid-tropospheric temperature change in Antarctica. Eos 89 (Fall meeting), abstr. C41A-0497
Cavalieri DJ, Parkinson CL (2008) Antarctic sea ice variability and trends, 1979–2006. J Geophys Res Oceans 113:C07004. doi:10.1029/2007JC004564
Chapman WL, Walsh JE (2007) A synthesis of Antarctic temperatures. J Clim 20:4096–4117
Comiso JC (2000) Variability and trends in Antarctic surface temperatures from in situ and satellite infrared measurements. J Clim 13:1674–1696
Comiso JC, Nishio F (2008) Trends in the sea ice cover using enhanced and compatible AMSR-E, SSM/ I, and SMMR data. J Geophys Res Atmos 113:C02S07. doi:10.1029/2007JC420057
Deser C, Phillips AS (2009) Atmospheric circulation trends, 1950–2000: the relative roles of sea surface temperature forcing and direct atmospheric radiative forcing. J Clim 22:396–413
Deser C, Phillips AS, Hurrell JW (2004) Pacific interdecadal climate variability: linkages between the tropics and North Pacific during boreal winter since 1900. J Clim 17:3109–3124
Deser C, Phillips AS, Alexander MA (2010) Twentieth Century tropical sea surface temperature trends revisited. Geophys Res Lett 37:L10701. doi:10.1029/2010GL043321
Ding Q, Steig EJ, Battisti DS, Kuttel M (2010) Recent West Antarctic warming caused by central tropical Pacific warming. Eos 90 (Fall meeting), abstr. A41D-0126
Evtushevsky OM, Grytsai AV, Klekociuk AR, Milinevsky GP (2008) Total ozone and tropopause zonal asymmetry during the Antarctic spring. J Geophys Res Atmos 113:D00B06. doi:10.1029/2008JD009881
Fogt RL, Perlwitz J, Monaghan AJ, Bromwich DH, Jones JM, Marshall GJ (2009) Historical SAM variability. Part II: twentieth-century variability and trends from reconstructions, observations, and the IPCC AR4 models. J Clim 22:5346–5365
Garreaud RD, Battisti DS (1999) Interannual (ENSO) and interdecadal (ENSO-like) variability in the Southern Hemisphere tropospheric circulation. J Clim 12:2113–2123
Genthon C, Krinner G (1998) Convergence and disposal of energy and moisture on the Antarctic polar cap from ECMWF reanalyses and forecasts. J Clim 11:1703–1716
Gloersen P, White WB (2001) Reestablishing the circumpolar wave in sea ice around Antarctica from one winter to the next. J Geophys Res-Oceans 106:4391–4395
Goosse H, Lefebvre W, de Montety A, Crespin E, Orsi AH (2009) Consistent past half-century trends in the atmosphere, the sea ice and the ocean at high southern latitudes. Clim Dyn 33:999–1016
Gregory S, Noone D (2008) Variability in the teleconnection between the El Nino-Southern Oscillation and West Antarctic climate deduced from West Antarctic ice core isotope records. J Geophys Res Atmos 113:D17110. doi:10.1029/2007JD009107
Hall A, Visbeck M (2002) Synchronous variability in the Southern Hemisphere atmosphere, sea ice, and ocean resulting from the annular mode. J Clim 15:3043–3057
Hanna E (1996) The role of Antarctic sea ice in global climate change. Prog Phys Geogr 20:371–401
Hansen J, Ruedy R, Glascoe J, Sato M (1999) GISS analysis of surface temperature change. J Geophys Res-Atmos 104:30997–31022
Hansen J, Reudy R, Sato M, Lo K (2010) Global surface temperature change. Rev Geophys 48:RG4004. doi:10.1029/2010RG000345
Holland MM, Raphael MN (2006) Twentieth century simulation of the Southern Hemisphere climate in coupled models. Part II: sea ice conditions and variability. Clim Dyn 26:229–245
Holland MM, Bitz CM, Hunke EC (2005) Mechanisms forcing an Antarctic dipole in simulated sea ice and surface ocean conditions. J Clim 18:2052–2066
Hurrell JW, Hack JJ, Phillips AS, Caron J, Yin J (2006) The dynamical simulation of the Community Atmosphere Model version 3 (CAM3). J Clim 19:2162–2183
Hurrell JW, Hack JJ, Shea D, Caron JM, Rosinski J (2008) A new sea surface temperature and sea ice boundary dataset for the Community Atmosphere Model. J Clim 21:5145–5153
Jacka TH, Budd WF, Holder A (2004) A further assessment of surface temperature changes at stations in the Antarctic and Southern Ocean, 1949–2002. Ann Glaciol 39:331–338
Jacobs SS, Comiso JC (1997) Climate variability in the Amundsen and Bellingshausen Seas. J Clim 10:697–709
Jin D, Kirtman BP (2009) Why the Southern Hemisphere ENSO responses lead ENSO. J Geophys Res 114:D23101. doi:10.1029/2009JD012657
Johanson CM, Fu Q (2007) Antarctic atmospheric temperature trend patterns from satellite observations. Geophys Res Lett 34:L12703. doi:10.1029/2006GL029108
Kanamitsu M, Ebisuzaki W, Woollen J, Yang SK, Hnilo JJ, Fiorino M, Potter GL (2002) NCEP-DOE AMIP-II reanalysis (R-2). Bull Am Meteorol Soc 83:1631–1643
King JC (1994) Recent climate variability in the vicinity of the Antarctic Peninsula. Int J Climatol 14:357–369
Kwok R, Comiso JC (2002) Spatial patterns of variability in antarctic surface temperature: connections to the Southern Hemisphere Annular Mode and the Southern Oscillation. Geophys Res Lett 29:1705. doi:10.1029/2002GL015415
Li S, Perlwitz J, Hoerling MP, Chen X (2010) Opposite annular responses of the Northern and Southern Hemisphere to Indian Ocean Warming. J Clim 23:3720–3738
Liu J, Curry JA (2010) Accelerated warming of the Southern Ocean and its impacts on the hydrological cycle and sea ice. Proc Nat Acad Sci 107:14987–14992
Liu J, Curry JA, Martinson DG (2004) Interpretation of recent Antarctic sea ice variability. Geophys Res Lett 31:L02205. doi:10.1029/2003GL018732
Marshall GJ (2007) Half-century seasonal relationships between the Southern Annular Mode and Antarctic temperatures. Int J Climatol 27:373–383
Meredith MP, King JC (2005) Rapid climate change in the ocean west of the Antarctic Peninsula during the second half of the twentieth-century. Geophys Res Lett 32:L19604. doi:10.1029/2005GL024042
Mo KC (2000) Relationships between low-frequency variability in the Southern Hemisphere and sea surface temperature anomalies. J Clim 13:3599–3610
Mo KC, Higgins RW (1998) The Pacific-South American modes and tropical convection during the Southern Hemisphere winter. Mon Weather Rev 126:1581–1596
Monaghan AJ, Bromwich DH, Fogt RL et al (2006) Insignificant change in Antarctic snowfall since the international geophysical year. Science 313:827–831
Monaghan AJ, Bromwich DH, Chapman W, Comiso JC (2008) Recent variability and trends of Antarctic near-surface temperature. J Geophys Res Atmos 113:D04105. doi:10.1029/2007JD009094
Mosley-Thompson E, Dai J, Thompson LG, Grootes PM, Arbogast JK, Paskievitch JF (1991) Glaciological studies at Siple Station (Antarctica)—potential ice-core paleoclimatic record. J Glaciol 37:11–22
Neff W, Perlwitz J, Hoerling M (2008) Observational evidence for asymmetric changes in tropospheric heights over Antarctica on decadal time scales. Geophys Res Lett 35:L18703. doi:10.1029/2008GL035074
Nicolas J, Bromwich DH (2010) Marine signature in West Antarctica. J Clim (in press)
O’Donnell R, Lewis N, McIntyre S, Condon J (2010) Improved methods for PCA-based reconstructions: case study using Steig et al. (2009) Antarctic temperature reconstruction. J Clim (in press)
Onogi K, Tslttsui J, Koide H et al (2007) The JRA-25 reanalysis. J Meteorol Soc Jpn 85:369–432
Parish TR, Bromwich DH (2007) Reexamination of the near-surface airflow over the Antarctic continent and implications on atmospheric circulations at high southern latitudes. Mon Weather Rev 135:1961–1973
Parkinson CL (2002) Trends in the length of the Southern Ocean sea-ice season, 1979–1999. Ann Glaciol 34:435–440
Perlwitz J, Pawson S, Fogt RL, Nielsen JE, Neff WD (2008) Impact of stratospheric ozone hole recovery on Antarctic climate. Geophys Res Lett 35:L08714. doi:10.1029/2008GL033317
Pritchard HD, Arthern RJ, Vaughan DG, Edwards LA (2009) Extensive dynamic thinning on the margins of the Greenland and Antarctic ice sheets. Nature 461:971–975
Raphael MN (2004) A zonal wave 3 index for the Southern Hemisphere. Geophys Res Lett 31:L23212. doi:10.1029/2004GL020365
Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, Rowell DP, Kent EC, Kaplan A (2003) Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res Atmos 108:4407. doi:10.1029/2002JD002670
Rayner NA, Brohan P, Parker DE, Folland CK, Kennedy JJ, Vanicek M, Ansell TJ, Tett SFB (2006) Improved analyses of changes and uncertainties in sea surface temperature measured in situ sice the mid-nineteenth century: the HadSST2 dataset. J Clim 19:446–469
Reynolds RW, Rayner NA, Smith TM, Stokes DC, Wang WQ (2002) An improved in situ and satellite SST analysis for climate. J Clim 15:1609–1625
Rignot E, Bamber JL, van den Broeke MR, Davis C, Li Y, van de Berg WJ, van Meijgaard E (2008) Recent Antarctic ice mass loss from radar interferometry and regional climate modelling. Nat Geosci 1:106–110
Robertson AW, Mechoso CR (2003) Circulation regimes and low-frequency oscillations in the South Pacific sector. Mon Weather Rev 131:1566–1576
Roscoe HK, Marshall GJ, King JC (2006) Low potential for stratospheric dynamical change to be implicated in the large winter warming in the central Antarctic Peninsula. Q J R Meteorol Soc 132:803–820
Santer BD, Wigley TML, Boyle JS, Gaffen DJ, Hnilo JJ, Nychka D, Parker DE, Taylor KE (2000) Statistical significance of trends and trend differences in layer-average atmospheric temperature time series. J Geophys Res-Atmos 105:7337–7356
Schneider T (2001) Analysis of incomplete climate data: estimation of mean values and covariance matrices and imputation of missing values. J Clim 14:853–871
Schneider DP, Steig EJ (2008) Ice cores record significant 1940s Antarctic warmth related to tropical climate variability. Proc Natl Acad Sci USA 105:12154–12158
Schneider DP, Steig EJ, Comiso JC (2004) Recent climate variability in Antarctica from satellite-derived temperature data. J Clim 17:1569–1583
Schwerdtfeger W (1976) Changes of temperature-field and ice conditions in area of Antarctic Peninsula. Mon Weather Rev 104:1441–1443
Shuman CA, Stearns CR (2001) Decadal-length composite inland West Antarctic temperature records. J Clim 14:1977–1988
Smith TM, Reynolds RW, Peterson TC, Lawrimore J (2008) Improvements to NOAA’s historical merged land-ocean surface temperature analysis (1880–2006). J Clim 21:2283–2296
Son S, Tandon NF, Polvani LM, Waugh DW (2009) Ozone hole and Southern Hemisphere climate change. Geophys Res Lett 36:L15705. doi:10.1029/2009GL038671
Stammerjohn SE, Martinson DG, Smith RC, Yuan X, Rind D (2008) Trends in Antarctic annual sea ice retreat and advance and their relation to El Nino-Southern Oscillation and Southern Annular Mode variability. J Geophys Res Oceans 113:C03S90. doi:10.1029/2007JC004269
Steig EJ, Schneider DP, Rutherford SD, Mann ME, Comiso JC, Shindell DT (2009) Warming of the Antarctic ice-sheet surface since the 1957 international geophysical year. Nature 457:459–463
Swanson GS, Trenberth KE (1981) Interannual variability in the Southern-Hemisphere Troposphere. Mon.Weather Rev. 109:1890–1897
Thoma M, Jenkins A, Holland D, Jacobs S (2008) Modelling circumpolar deep water intrusions on the Amundsen Sea continental shelf, Antarctica. Geophys Res Lett 35:L18602. doi:10.1029/2008GL034939
Thomas ER, Dennis PF, Bracegirdle TJ, Franzke C (2009) Ice core evidence for significant 100-year regional warming on the Antarctic Peninsula. Geophys Res Lett 36:L20704. doi:10.1029/2009GL040104
Thompson DWJ, Solomon S (2002) Interpretation of recent Southern Hemisphere climate change. Science 296:895–899
Turner J (2004) The El Nino-southern oscillation and Antarctica. Int J Climatol 24:1–31
Turner J, Colwell SR, Marshall GJ, Lachlan-Cope TA, Carleton AM, Jones PD, Lagun V, Reid PA, Iagovkina S (2004) The SCAR READER project: toward a high-quality database of mean Antarctic meteorological observations. J.Clim. 17:2890–2898
Turner J, Colwell SR, Marshall GJ, Lachlan-Cope TA, Carleton AM, Jones PD, Lagun V, Reid PA, Iagovkina S (2005) Antarctic climate change during the last 50 years. Int J Climatol 25:279–294
Turner J, Comiso JC, Marshall GJ, Lachlan-Cope TA, Bracegirdle T, Maksym T, Meredith MP, Wang Z, Orr A (2009) Non-annular atmospheric circulation change induced by stratospheric ozone depletion and its role in the recent increase of Antarctic sea ice extent. Geophys Res Lett 36:L08502. doi:10.1029/2009GL037524
Uppala SM, Kallberg PW, Simmons AJ et al (2005) The ERA-40 re-analysis. Q J R Meteorol Soc 131:2961–3012
van de Berg WJ, van den Broeke MR, Reijmer CH, van Meijgaard E (2006) Reassessment of the Antarctic surface mass balance using calibrated output of a regional atmospheric model. J Geophys Res Atmos 111:D11104. doi:10.1029/2005JD006495
van den Broeke MR (2000) On the interpretation of Antarctic temperature trends. J Clim 13:3885–3889
van den Broeke MR, van Lipzig NPM (2004) Changes in Antarctic temperature, wind and precipitation in response to the Antarctic Oscillation. Ann Glaciol 39(39):119–126
van den Broeke M, Reijmer C, van As D, Boot W (2006) Daily cycle of the surface energy balance in Antarctica and the influence of clouds. Int J Climatol 26:1587–1605
Vaughan DG, Bamber JL, Giovinetto M, Russell J, Cooper APR (1999) Reassessment of net surface mass balance in Antarctica. J Clim 12:933–946
Warren SG (1996) Antarctica. In: Encyclopedia of climate and weather 1. Oxford University Press, Oxford, pp 32–39
Weatherly JW, Walsh JE, Zwally HJ (1991) Antarctic sea ice variations and seasonal air-temperature relationships. J Geophys Res-Oceans 96:15119–15130
White WB, Peterson RG (1996) An Antarctic circumpolar wave in surface pressure, wind, temperature and sea-ice extent. Nature 380:699–702
Yuan X, Li C (2008) Climate modes in southern high latitudes and their impacts on Antarctic sea ice. J Geophys Res Oceans 113:C06S91. doi:10.1029/2006JC004067
Yuan XJ, Martinson DG (2000) Antarctic sea ice extent variability and its global connectivity. J Clim 13:1697–1717
Zhang Y, Wallace JM, Battisti DS (1997) ENSO-like interdecadal variability: 1900–1993. J Clim 10:1004–1020
Acknowledgments
The authors would like to thank A. Monaghan for his assistance with his Antarctic datasets, for many useful discussions, and for reviewing a draft of this manuscript. We also thank J. Arblaster and R. Tomas for updating the model simulations used here and A.S. Phillips for processing the model output. We thank three anonymous reviewers for their helpful suggestions. D.P. Schneider and Y. Okumura were supported by a grant from the National Science Foundation, Office of Polar Programs (ANT-0838871). The National Center for Atmospheric Research is sponsored by the National Science Foundation.
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Schneider, D.P., Deser, C. & Okumura, Y. An assessment and interpretation of the observed warming of West Antarctica in the austral spring. Clim Dyn 38, 323–347 (2012). https://doi.org/10.1007/s00382-010-0985-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-010-0985-x