Abstract
Processes acting at the interface between the land surface and the atmosphere have a strong impact on the European summer climate, particularly during extreme years. These processes are to a large extent associated with soil moisture (SM). This study investigates the role of soil moisture–atmosphere coupling for the European summer climate over the period 1959–2006 using simulations with a regional climate model. The focus of this study is set on temperature and precipitation extremes and trends. The analysis is based on simulations performed with the regional climate model CLM, driven with ECMWF reanalysis and operational analysis data. The set of experiments consists of a control simulation (CTL) with interactive SM, and sensitivity experiments with prescribed SM: a dry and a wet run to determine the impact of extreme values of SM, as well as experiments with lowpass-filtered SM from CTL to quantify the impact of the temporal variability of SM on different time scales. Soil moisture–climate interactions are found to have significant effects on temperature extremes in the experiments, and impacts on precipitation extremes are also identified. Case studies of selected major summer heat waves reveal that the intraseasonal and interannual variability of SM account for 5–30% and 10–40% of the simulated heat wave anomaly, respectively. For extreme precipitation events on the other hand, only the wet-day frequency is impacted in the experiments with prescribed soil moisture. Simulated trends for the past decades, which appear consistent with projected changes for the 21st century, are identified to be at least partly linked to SM-atmosphere feedbacks.
Similar content being viewed by others
1 Introduction
Climate extremes have a major societal, economical, and ecological impact, as for instance highlighted by the 2003 summer heat wave and drought in Europe (Larsen 2003; Heck et al. 2004; Ciais et al. 2005). Several recent observational (Klein Tank and Können 2003; Schmidli and Frei 2005; Alexander et al. 2006; Della-Marta et al. 2007) as well as modeling studies (Christensen and Christensen 2003; Meehl and Tebaldi 2004; Schär et al. 2004; Frei et al. 2006) report an increase in frequency and intensity of temperature and precipitation extremes, both for the recent past as well as for the coming decades.
The physical mechanisms underlying such changes in extremes of temperature and precipitation may relate to changes in large-scale circulation (Christensen and Christensen 2003; Meehl and Tebaldi 2004; Pal et al. 2004) and/or to changes in small-scale physical processes such as soil moisture–atmosphere interactions (Seneviratne et al. 2006b; Vidale et al. 2007).
Owing to the relevance of extremes, these research findings highlight the need for a better understanding of the contributing processes and feedbacks, which also implies comparison with observations (e.g. Ek and Holtslag 2004; Jaeger et al. 2009). Heat waves are generally caused by quasi-stationary anticyclonic circulation anomalies (Fink et al. 2004; Black et al. 2004; Meehl and Tebaldi 2004), sea surface temperature (SST) anomalies (Black and Sutton 2006), and/or land-atmosphere feedbacks (Seneviratne et al. 2006b; Fischer et al. 2007a, 2007b), whereby the latter can act as an amplifying mechanism. Similarly for precipitation variability and heavy precipitation events, both circulation patterns (Martius et al. 2006) and land–atmosphere feedbacks may be relevant (e.g. Beljaars et al. 1996; Schär et al. 1999; Pal and Eltahir 2002).
The impact of land–atmosphere coupling on climate is mainly determined by SM limitation on evapotranspiration (Seneviratne et al. 2010). Since large-scale field experiments investigating these effects are not feasible, one way of assessing the underlying mechanisms is to run climate model experiments with prescribed SM content (e.g. Koster et al. 2004; Seneviratne et al. 2006b; Rowell and Jones 2006; Fischer et al. 2007a; Conil et al. 2007). This method allows to infer causal relationships regarding the effect of SM on climate, since the two-way coupling of the atmosphere and SM is removed, and the experiments thus investigate only the one-way effect of SM on the atmosphere, whereas the atmosphere has no influence on SM. Here, this procedure is used to disentangle the effect of SM variability on different time scales, as well as to investigate the impact of extreme levels of SM on the current European summer climate. To this aim a set of regional climate model (RCM) experiments are performed using the CLM RCM (Sect. 2.1) driven with reanalysis and operational analysis data from ECMWF. Thereby, the main focus of the present study is on impacts of SM on extremes and trends in temperature and precipitation. The analysis is performed for the summer season, when oceanic impacts on climate are small compared to SM impacts over mid-latitudinal land areas (e.g. Koster and Suarez 1995).
One can distinguish three different approaches for the analysis of climate extremes. A first group considers directly the probability density functions (PDFs) of the investigated variables, generally temperature or precipitation (Alexander et al. 2006; Perkins et al. 2007), and thereby focuses on their tail behaviour. Since most statistical distribution functions do not well describe the tail behaviour of the underlying data, a second group of studies uses techniques of extreme value theory (EVT) that provide special distribution functions for extremes. The study of Frei et al. (2006) for instance uses EVT to assess the future change of precipitation extremes in Europe based on a set of RCM experiments from the EU-project PRUDENCE (http://prudence.dmi.dk). Other modeling studies use EVT to assess changes of temperature extremes (e.g. Zwiers and Kharin 1998; Kharin and Zwiers 2000). There are also several observational studies assessing changes in temperature extremes using EVT, which report an increase at least in the location (some also in the shape) of the used extreme value distribution (e.g. Laurent and Parey 2007; Della-Marta et al. 2007; Brown et al. 2008). Finally, a third group of studies uses so called climate extreme indices to capture a variety of aspects of climate extremes both in models (e.g. Frei et al. 2006; Fischer et al. 2007a; Kjellström et al. 2007) and observations (e.g. Klein Tank et al. 2002; Schmidli and Frei 2005; Della-Marta et al. 2007). Wet, dry, hot or cold events can be extreme in terms of frequency, duration or intensity, and these aspects cannot be investigated from the analysis of temperature and precipitation PDFs only. As an example, the EU-FP6 project CECILIA (http://www.cecilia-eu.org/) established a list of more than 130 indices characterizing temperature and precipitation statistics.
Beside the analysis of the role of SM for climate extremes, we also assess in this study the possible impact of SM on climate trends. The investigation of trends and their relation to possible changes in drivers or feedback processes has received increasing interest in the climate community due to climate change. For climate extreme indices, the analysis of trends is mainly performed using either parametric methods (e.g. regression models (Klein Tank and Können 2003; Schmidli and Frei 2005) or non-stationary extreme value analysis (e.g. Kharin and Zwiers 2005)), or non-parametric methods (e.g. robust slope estimator Theil-Sen (Alexander et al. 2006) or digital filters (Tebaldi et al. 2006)).
The outline of this paper is as follows. Section 2 presents the setup of the numerical experiments and the statistical procedure that was used for their analysis. Then, Sect. 3 assesses the impact of the temporal variability and extreme values of SM for mean climate properties. Section 4 provides a thorough analysis of temperature and precipitation extremes and their link to SM for long-term climatologies, whereas in Sect. 5, the focus is set on the representation of specific observed extreme events in the simulations. Then, in Sect. 6, simulated trends in daily temperature and precipitation (mean and extremes) are calculated, and linked to SM and related physical processes. Section 7 briefly compares CTL to observations and to other state-of-the-art RCMs to provide an evaluation of the employed model. Finally, the main results are summarized in Sect. 8.
2 Data and methodology
2.1 The CLM regional climate model experiments
2.1.1 CLM setup
In this study we use the CLM RCM, which is the climate version of the non-hydrostatic COSMO model (COnsortium for Small-scale MOdeling: http://cosmo-model.cscs.ch/) employed by several European weather services for numerical weather prediction. A similar model configuration is adopted as for the EU-FP6 project ENSEMBLES (http://www.ensembles-eu.org) (Jaeger et al. 2008).Footnote 1 The employed model version (2.4.11) was identified as having significantly smaller biases than a more recent version (4.0, see Jaeger et al. 2008), and is thus used in the present study. It was also validated with regard to land-atmosphere coupling characteristics with FLUXNET observations (Jaeger et al. 2009).
We integrate CLM over a domain covering the entire European continent, with 0.44° (≈50 km) horizontal resolution, 32 levels in the vertical and 10 soil layers. Lateral boundary conditions are derived from the ERA40 reanalysis (1958–2001, Uppala et al. 2005) and from ECMWF operational analysis (2002–2006). The initial conditions correspond to the climatological values of a long-term CLM simulation to ensure that the model is approximately within its equilibrium. The external parameters are derived from AVHRR data for the vegetation parameters (leaf area index, plant cover and root depth) and from the FAO 1995 digital soil map for soil types (9 classes in CLM).
Our CLM configuration uses Leapfrog numerics, Tiedtke (1989) convection based on a moisture-convergence closure, a radiative transfer scheme based on Ritter and Geleyn (1992), vertical turbulent diffusion using prognostic turbulent kinetic energy (Raschendorfer 2001), the second-generation multi-layer soil model TERRA-ML (Schrodin and Heise 2002) with both bare-soil evaporation and transpiration being calculated following Dickinson (1984). More details on the model dynamics and physics are available in Steppeler et al. (2003) and Will et al. (2010) or in the model documentation (available from http://www.clm-community.eu/).
2.1.2 Sensitivity experiments
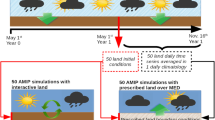
In order to assess the possible impact of extreme values and of the temporal variability of SM on the European summer climate, a set of sensitivity experiments with different prescribed SM evolutions was performed (see Table 1 for an overview). Note that in the prescribed SM experiments, soil moisture is not altered by any surface fluxes, nor by precipitation or runoff. A reference simulation includes interactive SM, and will be referred to as CTL hereafter.
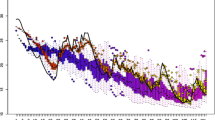
In two of the sensitivity experiments, SM is set to its minimum (plant wilting point, PWP) and maximum (field capacity, FCAP) value for each grid point and model soil layer separately depending on the respective model soil type. The aim of these simulations is to assess the impact of extreme values of SM on climate. In addition, a set of more subtle prescribed SM experiments was performed, with the aim of assessing the impact on climate of temporal SM variability on different time scales. In order to disentangle the effects of synoptic-scale, intraseasonal, and interannual SM variability, the soil moisture time series from CTL are subsequently filtered using a digital low-pass filter (details in “Appendix 1”) applied separately for each of the model’s soil layers, and at each grid point over the entire model domain. A first experiment removes the synoptic-scale variability (called SSV) by filtering out SM variations below roughly ten days. A second experiment additionally removes the intraseasonal variability (called ISV) from SSV by filtering out SM variations below roughly 100 days. Finally, for the so called IAV experiment, we also remove the interannual variability from ISV, resulting in a similar experimental setup as in Seneviratne et al. (2006b) and Fischer et al. (2007a). See Fig. 1 for an illustration of the SM values of these five model experiments in comparison with the control simulation.
Illustration of the soil moisture evolution (m) of the different CLM experiments (see Table 1) for a grid point from the Iberian Peninsula. Shown is the 2nd model soil level for the period 2002–2005
2.2 Observations and ENSEMBLES model simulations
Though the employed model version has already been extensively validated (Jaeger et al. 2008, 2009), we additionally briefly compare the results of the CTL simulation with observations and (re)analysis data (hereafter referred to as OBS) in Sect. 7, with a focus on temperature and precipitation extremes and trends. For the validation we use the gridded E-OBS dataset (version 1.0) of the EU-FP6 project ENSEMBLES for temperature and precipitation (Haylock et al. 2008), and ERA40 reanalysis (Uppala et al. 2005) for the total cloud cover. For the validation of temperature we apply a height correction using a constant lapse rate of −0.65 K/100 m in order to properly compare model and observations.
Moreover, to assess the performance of CLM in comparison with other state-of-the-art RCMs, regional climate simulations from the ENSEMBLES archive are analysed and compared to CLM for the period 1961–2000 (Sect. 7). The following ERA40 reanalysis-driven RCM simulations with 25 km horizontal resolution were used: RCA (simulation from the C4I and SMHI institutes), Aladin (CNRM), HIRHAM (DMI and METNO), CLM (ETHZ, see also Jaeger et al. 2008), HadRM (HC), RACMO (KNMI), REMO (MPI), and PROMES (UCLM). For temperature and precipitation extremes we additionally analysed Aladin (CHMI) and RegCM (ICTP).
2.3 Analysis methodology
The main focus of this study is on the impact of SM on climate extremes and trends thereof. The analysed variables are daily maximum temperature (T max ) and daily mean (and/or wet-day) precipitation. The analysis focuses on climate extreme indices, derived probability density functions, and the explicit modeling of climate extremes using extreme value theory.
2.3.1 Indices
Table 2 lists climate extreme indices considered in this study, which correspond to a subset of the total number of indices considered in the EU-project CECILIA. In order to test for statistically significant differences between CTL and the sensitivity experiments, we perform tests at every grid point. Due to the multiplicity problem of independent tests and the spatial dependency of neighbouring grid points, the outcoming result can only be viewed as a crude estimate. More reliable estimates of significance could be obtained using resampling methods (e.g. see Wilks 2006 and references therein, or Wilks 1997). However, this is not feasible in our case due to the computational constraints associated with the size of the considered datasets. Here, our approach is the following: First, we calculate extreme indices for each of the 48 years (1959–2006) separately. Then, we compare the empirical distribution of these 48 values using a two-sided Kolmogorov–Smirnov test (details in “Appendix 2”). We then compute the area-weighted fraction of land points with statistically significant differences at the 5% level and display maps of the yearly extreme indices averaged over the 48 years. Note that for int, freq or perc95 it does not make a difference whether the indices are calculated over the whole period of interest (CECILIA definition) or first separately for each year and then averaged over all years. In order to ease the computation of significance (see above) we use for simplicity the latter definition for these indices. However, in the case of the hwdi indices \((hwdi_{max}, hwdi_{max}^{\ast}, hwdi_{mean}, hwdi_{mean}^{\ast}),\) values calculated separately for each year and then averaged over all years differ from values calculated over the whole period. In order to follow the CECILIA definitions, the hwdi indices are calculated over the whole period and, hence, statistical significance is not assessed for these indices.
2.3.2 PDFs
Additionally, we qualitatively investigate the PDFs of daily precipitation and of T max , by fitting a Gamma distribution and applying a kernel density estimation, respectively, to the PRUDENCE subdomain mean time series (for a map of the subdomains see Christensen and Christensen 2007). Moreover, we also display the PDFs of seasonal extreme values (block maxima) of daily precipitation and of T max using a Generalized Extreme Value distribution (see below). Again, we apply a two-sided Kolmogorov–Smirnov test to assess statistically significant differences. In order to quantitatively compare the PDFs, we also compute statistical indices describing the raw data underlying the PDFs (mean, standard deviation, 99th-percentile, inter-quartile range, skewness).
2.3.3 EVT
Finally, we statistically model temperature and precipitation extremes using extreme value theory. For this, we employ the block maxima technique on a grid point basis, which is based on the so called Generalized Extreme Value (GEV) distribution (e.g. Coles 2001), but we neglect spatial dependency among the neighbouring grid points (Coelho et al. 2008). The GEV is a three-parameter distribution function with location μ, scale σ and shape ξ parameters. The analysis is based on yearly blocks (48 values for the period 1959–2006) each computed from 92 daily values for JJA. For precipitation extremes we use a modified form of the classical GEV likelihood function to estimate the parameters of the GEV distribution, which includes a Bayesian prior distribution for ξ (Frei et al. 2006). This is done in order to avoid absurd values of ξ if conventional maximum likelihood estimation from small samples is used. Therefore, we apply a Beta distribution as a Bayesian prior, which totally prevents estimates outside (−0.5, +0.5) (Martins and Stedinger 2000). Of primary interest are then multi-year return values that are calculated based on the fitted GEV distribution (see Table 2), as well as the GEV distribution itself for PRUDENCE subdomain mean time series. At least for temperature extremes the difference in the return values calculated with or without a prior for ξ is small and, hence, we use here the simpler model. Uncertainty is inferred from bootstrap simulations also at the grid point basis, and tests for statistically significant differences between CTL and experiments are obtained using a similar approach as in Kharin and Zwiers (2000) (details in "Appendix 2", non-parametric bootstrap tests). In order to assess the robustness of our results obtained using the block maxima approach, we have alternatively applied a stationary peak-over-threshold model (e.g. Coles 2001). This model yields similar return values as in the block maxima approach (not shown).
3 Impact of soil moisture variability on European mean summer climate
This study focuses on the possible impact of soil moisture on climate extremes and trends (Sects. 4, 5, 6). In this section we first analyse briefly the mean climate characteristics of the conducted experiments. Note that the SSV, ISV and IAV experiments share the same mean SM seasonal cycle as CTL (and only differ with regard to their SM variability, Fig. 1). Hence, one does not expect a systematic impact of the prescribed SM fields on the mean climate of these simulations, though possible effects cannot fully be excluded, e.g. if part of the climate response depends non-linearly on the SM content. The net effects on the mean climate of SSV, ISV and IAV are indeed small (not shown), and we exemplarily focus here only on IAV, as it shows the largest effect.
Figure 2 displays the mean temperature, total and convective precipitation, net shortwave radiation (SW net ), total net radiation (R net ) and geopotential height patterns in CTL, and the respective differences between the sensitivity experiments IAV, PWP, FCAP and CTL. In the case of FCAP, the increase in SM leads to an increase in latent (LE) and a decrease in sensible (H) heat flux (and therefore also in the Bowen ratio, not shown). This causes a shallower, moister and colder planetary boundary layer (PBL) as indicated by the decreased 2m-temperature (T 2m), the analysis of atmospheric profiles (Fig. 3), as well as by an increased total cloud cover (not shown). As a consequence, SW net decreases and the net longwave radiation (LW net , not shown) increases. The increase in the total cloud cover leads to an increase in precipitation, i.e. to a positive SM-precipitation feedback. PWP presents the opposite behaviour due to the imposed drier SM conditions, except for R net (see below).
Summer climatologies (1959–2006) of the impact of SM variability on the mean climate: T 2m (K, 1st row), total precipitation (mm/d, 2nd row), convective precipitation (mm/d, 3rd row), SW net (W/m2, 4th row), R net (W/m2, 5th row) and geopotential height at 500 hPa (m, 6th row). From left to right CTL, IAV-CTL, PWP-CTL and FCAP-CTL are shown. Note that colourbars are different for CTL and the difference plots and irregular in the latter case. The numbers in the lower-right corner give the area weighted fraction of land points at which the null hypothesis of ‘being from the same distribution’ is rejected at the 5% level according to the two-sided Kolmogorov–Smirnov test
Boundary layer tephigram of the atmospheric profiles of all CLM experiments (labeled are temperature T in solid lines, pressure p in dashed lines and specific humidity q in doted lines; additionally the dry and wet adiabates are given in solid lines perpendicular to T and dashed–dotted lines, respectively). Shown is a mean profile at 12 UTC for the summer (JJA) period, averaged over 1959–2006 for the French PRUDENCE subdomain. Time and space averaging (48-year JJA, PRUDENCE areas, land-only) is performed on model levels. Note that the moisture and temperature profiles for the CTL, SSV, ISV and IAV experiments are very similar and, hence, partly overlap each other
Note that the anomalies in R net for the FCAP and PWP simulations (Fig. 2) suggest that the response of R net , at least in our simulations, does not present a clear relationship with soil moisture content. For instance, in Eltahir et al. (1998) and Schär et al. (1999), it was suggested that moist conditions would lead to an enhanced R net at the surface, a result opposite to the sensitivity displayed by the FCAP simulation. On the other hand, our dry simulation (PWP) also shows a diminished R net , and thus these effects do not appear to be symmetric for decreased/increased SM. More analyses would be needed to shed light on this asymmetric response.
Regarding the anomalies in the IAV simulation, as mentioned, this experiment (similar to SSV and ISV) displays only a weak modification of the mean climate: SM is drier than CTL in wet years, and wetter than CTL in dry years. Interestingly, despite the weak signal, the anomalies are consistently of the same sign as in FCAP, although the IAV experiment is not systematically wetter than CTL. This suggests that the wetting effects in dry years have stronger impacts than the drying effects in wet years and, hence, that there is some degree of non-linearity in the response of European climate to SM forcing (i.e. stronger impact in dry years). This is consistent with the fact that 20th century European climate is characterized on average by humid conditions, i.e. evapotranspiration is close to its potential value on average and is only significantly modified under drier conditions (see e.g. Seneviratne et al. 2010 for more details).
Mean precipitation was further decomposed into large-scale and convective precipitation, and Fig. 2 displays the anomalies for the convective fraction of precipitation. For IAV (as well as SSV and ISV), the partitioning between the two precipitation components is similar as in CTL. In contrast, for FCAP, the increase in mean precipitation comes mostly from an increase in convective precipitation (partly also true for the precipitation decrease in PWP).
Finally, Fig. 2 also points to the strong impact of SM changes on the geopotential height in the sensitivity experiments, similar to the effects identified in experiments with modified SM for the 2003 heat wave in Europe with another RCM (Fischer et al. 2007b). However, one has to keep in mind that such large geopotential height anomalies are constrained by the employed setup of the RCM simulations, since they cannot interact with the imposed large-scale circulation patterns.
4 Impact of soil moisture variability on European summer climate extremes
This section focuses on the impact of extreme values and the temporal variability of soil moisture on European temperature and precipitation extremes. In a first part, we assess the extreme diagnostics listed in Table 2 for CTL. Then, in a second part, the extreme diagnostics are analysed for the sensitivity experiments. Finally, in a third part, mean subdomain PDFs of daily T max and precipitation are analysed, for both CTL and the sensitivity experiments.
4.1 Temperature extremes
4.1.1 Geographical patterns: CTL
Figure 4 (left panels) displays the daily T max diagnostics for CTL. The 95th-percentile (perc95) and particularly the 50-year return value (ret50) describe the upper tail of the daily T max distribution. These two indices exhibit similar geographical patterns, with a North-South and an East-West gradient. This suggests that both indices tend to increase with drier climatic conditions. The maximum heat wave duration index hwdi max assesses the atmospheric tendency for persistence at the upper tail of the daily T max distribution. The spatial patterns of this diagnostic are therefore different from those of perc95 and ret50, with largest values in the Mediterranean and in Western and Northern Europe. Note, however, that we cannot necessarily expect a North-South gradient in this diagnostic since we calculate it with respect to the local 90th-percentile rather than with respect to a fixed threshold value. In the Scandinavian subdomain for instance, the 90th-percentile is ≈10 K lower than in the Iberian Peninsula subdomain. The overall pattern in hwdi max suggests higher values for regions neighbouring oceans, possibly indicating an effect of persistence associated with SSTs. The patterns of hwdi mean are slightly different with largest values in the Mediterranean and in Eastern and Northern Europe (see Fig. 2 in Lorenz et al. 2010).
Summer climatologies (1959–2006) of the impact of SM variability on T max extreme diagnostics: perc95 (K, 1st row), hwdi max (with respect to 90th-percentile of CTL (d, 2nd row), \(hwdi_{max}^{\ast}\) (with respect to 90th-percentile of respective experiment (d, 3rd row), and ret50 (K, 4th row) as estimated by stationary block maxima analysis. From left to right CTL, SSV-CTL, ISV-CTL, IAV-CTL, PWP-CTL and FCAP-CTL are shown. The numbers in the lower-right corner give a measure for the statistical significance (see Fig. 2)
4.1.2 Geographical patterns: sensitivity experiments
In this subsection we discuss the differences of the analysed T max diagnostics between the sensitivity and CTL experiments (Fig. 4). The anomalies in perc95 and ret50 between the sensitivity experiments and CTL show very similar patterns, with increasingly larger difference from SSV over ISV to IAV and highest impacts in Scandinavia and Central Europe. Note, however, that differences are significant over larger coherent areas for IAV only (>65 % of European area). For FCAP and PWP the differences are significant for most parts of Europe with largest signals over Central and Northern Europe for PWP, and over Eastern and Southern Europe for FCAP. This can be easily understood since in Eastern and Southern Europe, SM is close to the plant wilting point in CTL, while in Central and Northern Europe it is close to the field capacity. For hwdi max we find similarly a continuous decrease from SSV over ISV to IAV, with largest differences over Scandinavia and Central Europe, and most pronounced effects in FCAP and PWP. The index \(hwdi_{max}^{\ast}\) is computed using the 90th-percentile of the respective simulation instead of CTL (see Table 2). This allows to distinguish between changes in heat wave duration induced by changes in the respective PDFs of daily T max , or by changes in atmospheric persistence. Lorenz et al. (2010) provide a detailed discussion of the implications of using these different thresholds for hwdi indices. The \(hwdi_{max}^{\ast}\) values exhibit clear reductions in the IAV, PWP and FCAP experiments. This can be understood by the fact that in these simulations SM persistence is removed, since long spells of SM anomalies are not allowed by the set-up. Hence, one source of atmospheric persistence, namely soil moisture memory, is shut down (see also Lorenz et al. 2010). We see from the response of the IAV experiment that it is the memory associated with interannual SM anomalies that is mostly relevant.
4.1.3 Probability density functions (PDFs)
In this subsection, we assess the PDFs of daily T max in the simulations for several European subdomains as defined in the EU-project PRUDENCE (e.g. Christensen and Christensen 2007). Results are exemplarily displayed for the France subdomain in Fig. 5 (top panel). Analyses for the other European subdomains are provided in the supplementary information (Fig. S1). Since we do not want to mix spatial and temporal variability, and the former is already analysed in Fig. 4, we assess here PDFs of mean subdomain daily T max (Fig. 5, top panel). Hence, one should not compare the percentiles of the PDFs in Fig. 5 (top panel) with those shown in Fig. 4.
PDFs of daily T max (K) for France subdomain (top; using a kernel density estimation) and of summer T max block maxima (K) (bottom; using a GEV fit). The PDFs are based on the mean subdomain values and the summer period 1959–2006. Simulations with bold legend entries are significantly different from CTL at the 5% level according to the two-sided Kolmogorov–Smirnov test
The analysis reveals that only the T max PDFs of the PWP and FCAP simulations are significantly different from CTL for all eight subdomains. ISV and IAV are generally significantly different from CTL (except for France and also for the Iberian Peninsula in the case of ISV). SSV on the other hand is only significantly different from CTL for the Alpine region. Additionally, some statistical quantities describing the data underlying the PDFs are listed in Table S1 in the supplementary material. For PWP and FCAP most statistical quantities are again significantly different from CTL, in contrast to SSV. Note that also for IAV, the measures characterising the tails or the spread of the distributions are significantly smaller (to a lesser extent also true for ISV). This is consistent with the results of the previous sections: Largest differences of daily T max are found for PWP and FCAP; from the experiments modifying the temporal SM variability, in general only IAV displays significant impacts. Interestingly, PWP (FCAP) exhibits a pronounced widening (narrowing) of its PDF, which is due to the removed (increased) damping effect of SM—through evaporative cooling—on the temperature extremes at the high end (i.e. hot extremes). The distinct impact of SM is clearly recognizable from the asymmetric effects on the PDFs.
The bottom panel of Fig. 5 displays the corresponding PDFs for the summer block maxima of daily T max (note that block maxima are the basis for the GEV used to obtain ret50 in Fig. 4). These PDFs are shifted to higher temperatures and they are narrower compared to the PDFs of daily T max discussed above. While the differences of the sensitivity experiments seem to be more pronounced than for the PDFs of daily T max , the statistical analysis reveals slightly lower significance. This is mainly due to the smaller sample size (48 values compared to 92 × 48 values for the PDFs of daily T max ). As identified for the overall PDFs, we see that SM has a strong impact mainly on temperature maxima, which can be understood from the presence or lack of evaporative cooling.
In summary, we identify the following effect of SM on the European summer temperature (maxima). Reducing the temporal soil moisture variability reduces the temperature extremes. We find that it is the interannual variability of SM that is most relevant in this respect. Imposing extreme mean values of soil moisture also has a large impact: Wet soils (as in FCAP) cause a decrease in temperature extremes, mainly in arid areas, and dry soils (as in PWP) an increase, mainly in humid areas. These effects are asymmetric and impact temperature maxima more strongly than temperature minima. This is consistent with a non-linear dependency of surface fluxes on soil moisture (e.g. Koster et al. 2004, Seneviratne et al. 2010), i.e. the existence of distinct regimes with little vs. high sensitivity to soil moisture (in wet, respectively drier, soil moisture conditions).
4.2 Precipitation extremes
4.2.1 Geographical patterns: CTL
Figure 6 (left panels) displays the daily precipitation diagnostics in CTL. Both perc95 and particularly ret50 describe the upper tail of the daily precipitation distribution. Accordingly, they both exhibit similar geographical patterns with maximum values in Central and Eastern Europe, particularly over the Alps, though the patterns of ret50 are generally noisier. The diagnostics 5dmax and ret505d , which describe the upper tail of the 5-day precipitation distribution, display similar patterns as the daily precipitation extreme diagnostics (not shown). Hence, as to be expected for Europe, summer precipitation in the simulations is mainly of convective nature, and long-term precipitation events, which are more common in autumn and winter, are rare. The other two diagnostics, the mean wet-day intensity (int) and frequency (freq), do not describe the upper tails of the precipitation distribution. Nevertheless, int exhibits a similar pattern as the daily diagnostics described before, whereas freq presents similar geographical patterns as the mean summer precipitation (see Fig. 2).
As in Fig. 4 but for the daily precipitation extreme diagnostics: perc95 (mm/d), int (mm/d), freq (fraction), and ret50 (mm/d) (from top to bottom)
4.2.2 Geographical patterns: sensitivity experiments
Figure 6 also displays the differences between the sensitivity and CTL experiments for the analysed precipitation diagnostics. It is striking that the three experiments with modified temporal SM variations (SSV, ISV, IAV) do not significantly differ from CTL for any of the analysed statistical indices. Hence, the difference patterns show mostly noise, except for decreased freq. Indeed, the statistical tests do not reveal significant differences in any European area. For PWP and FCAP the differences are however much larger and more significant. The most striking difference is found for freq: In the dry experiment (PWP) there is a lower wet-day frequency than in CTL. Similarly, the wet experiment (FCAP) shows a higher wet-day frequency than CTL. This suggests that SM is highly relevant to the triggering of precipitation events in the experiments. However, on wet days, the precipitation characteristics are similar in the three simulations (CTL, PWP, FCAP) as indicated by int, perc95 and ret50. There is a small tendency for both PWP and FCAP to have smaller values of perc95 and int: for PWP in Southern and Northern Europe, and for FCAP in Central and Eastern Europe. For ret50 PWP has slightly smaller return values (FCAP larger ones) compared to CTL, however, this result is hardly significant. On the contrary, 5dmax differs more substantially with significant reductions across the whole of Europe for PWP and increases (though only significant in Southern Europe) for FCAP (not shown). This is due to the large differences in wet-day frequency in the simulations.
As displayed in Fig. 8, for both PWP and FCAP, the changes in freq are mostly due to changes in the frequency of convective precipitation, whereas the changes in int are mostly due to changes in the intensity of large-scale precipitation (compare with freq and int of PWP and FCAP in Fig. 6).
4.2.3 Probability density functions (PDFs)
The PDFs of mean subdomain daily precipitation are displayed exemplarily for the France subdomain in the top panel of Fig. 7 and statistical quantities describing the data underlying the PDFs are listed in Table S2 in the supplementary material. PDFs for other PRUDENCE subdomains are also provided in the supplementary material (Fig. S2). As mentioned for the temperature PDFs, one should not try to compare the percentiles of the PDFs with those shown in Fig. 6, since they are derived from subdomain mean daily precipitation values (see comment in Sect. 4.1.3)
The same as in Fig. 5 but for mean France subdomain precipitation (mm/d) larger than 1 mm/d. Note that for the daily precipitation fit (top) we use a Gamma distribution and for the daily precipitation block maxima (bottom) again the GEV distribution
From left to right: int of PWP-CTL, int of FCAP-CTL, freq of PWP-CTL, freq of FCAP-CTL for convective precipitation (top row), and for large-scale precipitation (bottom row) for the summer period 1959–2006. The corresponding panels for the total precipitation were already shown in Fig. 6
Generally, the PDFs for SSV, ISV and IAV are not significantly different from CTL for any European subdomain. On the contrary, the PDFs of FCAP and PWP are significantly different from CTL at least for some subdomains (but with larger differences for PWP than FCAP). Most of the analysed statistical quantities are not significantly different between CTL and the sensitivity experiments, except for PWP (partly also true for FCAP) with e.g. a smaller mean and inter-quartile range for PWP. The same holds for the PDFs of the summer block maxima of daily precipitation shown in the bottom panel of Fig. 7. However, there is a striking shift towards higher precipitation amounts, and, in contrast to the temperature PDFs discussed above, a widening of the PDFs compared to the PDFs for the daily precipitation.
Overall, the temporal soil moisture variablity does not appear to have an impact on the European summer daily precipitation distribution. Changes in the absolute amount of available SM, as investigated in the PWP and FCAP experiments, mostly affect the precipitation frequency and, hence, the absolute mean of European summer daily precipitation (as well as 5dmax). However, the characteristics of the European summer daily precipitation distribution on wet days remain similar for most experiments. Note that a recent study by Brockhaus et al. (2010) reveals that CLM with a convection scheme based on more sophisticated physics (ECMWF IFS) produces more realistic daily precipitation and exhibits a smaller positive SM-precipitation feedback.
5 Selected case studies of climate extremes
5.1 Heat waves
In a previous study with the CHRM RCM focusing on four summer heat waves (1976, 1994, 2003 and 2005) (Fischer et al. 2007a), the number of hot summer days (nhd) of a ‘IAV-type’ experiment was reduced by roughly 50–80% compared to a CTL experiment. In order to directly compare our experiments to the results obtained by Fischer et al. (2007a), we provide here comparable analyses for the 1976, 1994, 2003 and 2005 heat waves based on our present experiments (Fig. 9 exemplarily displays the 2003 case, and results for all four heat waves are summarized in Fig. 10). The overall patterns as well as the amount of nhd agrees very well between the two studies (note that Fischer et al. (2007a) give nhd in days, whereas we use the CECILIA definition which uses fraction). For the 2003 heat wave, the reduction of nhd from CTL to SSV (synoptic-scale variability) is very small and mostly confined to Central and Southern Europe, with values of 5% for the area where the heat wave was the strongest (France and Switzerland). There is some decrease for ISV, particularly in Southern, in Central but also in Northern Europe. Compared to CTL the reduction for the same areas is of roughly 6%, whereas most of the decrease in these areas is indeed present in the IAV experiment, with values of roughly 36%. If we also take into account the other heat wave summers 1976, 1994 and 2005, we obtain a reduction of nhd of 5–10% for SSV-CTL, 10–40% for ISV-CTL, and 40–70% for IAV-CTL (Fig. 10), similar to the value of 50–80% found in Fischer et al. (2007a). Note, however, that the IAV experiment removes at the same time the interannual, intraseasonal, and synoptic-scale variability. Using the experiments of the present study, we can additionally distinguish the single contribution of synoptic-scale (SSV-CTL), of intraseasonal (ISV-SSV) and of interannual (IAV-ISV) variability to the total temperature anomalies in the selected heat wave summers. The experiments suggest that these correspond to 5–10% for the synoptic-scale, and 5–30% for the intraseasonal variability, compared to 10–40% for the interannual variability (again for France and Switzerland).
From top to bottom: nhd (fraction), hwdi max (d) and \(hwdi_{max}^{\ast}\) (d) of summer 2003 with respect to long-term 90th-percentile of CTL simulation (of experiment for \(hwdi_{max}^{\ast}\)). Note that for CTL: \(hwdi_{max} = hwdi_{max}^{\ast}\). From left to right: CTL, SSV-CTL, ISV-CTL, IAV-CTL, PWP-CTL, FCAP-CTL
Fractional difference ((EXP − CTL)/CTL) (%) between the experiment (left panel: SSV, ISV, IAV; right panel: PWP, FCAP) and CTL for nhd (top panel), hwdi max (middle panel), and \(hwdi_{max}^{\ast}\) (bottom panel) for all summers discussed in Fischer et al. (2007a). Shown are average values for the area where the heat waves were strongest (France and Switzerland for 1976, 2003, 2005; France and Central Europe for 1994). Note the different scales on the y-axes (right panel)
Hence, our experiments confirm that the interannual variability of SM is the largest contributor to the heat wave extremes (as assessed with nhd), but we find that the contribution of at least the intraseasonal SM variability is of comparable magnitude. Finally, note that we find again the largest change for the ‘extreme experiments’ PWP and FCAP (Fig. 10, right panel), which provide us some insights on the maximum possible effect of SM in the considered heat waves. In PWP, nhd is more than doubled in all four heat waves, while it is close to zero (i.e. decrease close to 100%) in FCAP. This suggests that the already extreme heat waves in 1976, 1994, 2005, and particularly 2003, could have been even more extreme in case of total depletion of soil moisture.
In order to assess the impact of SM on the duration of the heat waves, Figs. 9 and 10 also display the two heat wave indices hwdi max and \(hwdi_{max}^{\ast}\) that were previously analysed over the whole simulation period in Sect. 4.1.2. While the differences in hwdi max exhibit similar patterns as those for nhd discussed above, the differences in \(hwdi_{max}^{\ast}\) present distinct patterns. Given the use of the long-term 90th-percentile of the respective sensitivity experiment as hot day threshold for \(hwdi_{max}^{\ast}\) this allows to leave aside changes in heat wave duration induced by modification of the T max PDFs in the sensitivity experiments and focus rather on impacts of soil moisture memory for heat wave persistence (see also Lorenz et al. (2010) for hwdi mean versus \(hwdi_{mean}^{\ast}\)). The results for the IAV experiment suggest thus that the impact on heat wave duration due to removed persistence alone is possibly large compared to the differences due to the changes in absolute soil moisture content. Hence, the large difference in heat wave duration found both in Fischer et al. (2007a) and in the present study might not only be due to differences in the absolute SM content but also to differences in soil moisture persistence.
5.2 Heavy convection episodes
In the previous sections it was shown that the CLM setup used in this study exhibits a positive soil moisture-precipitation feedback, when extreme values of SM are prescribed (PWP, FCAP). However, on wet days it was found that the precipitation characteristics are hardly affected by SM variations, and that the net resulting effect is mostly induced by a change in the frequency of precipitation events with SM. Therefore, we additionally analysed several single summer months with increased convective activity, and focused on regions that are particularly interesting in this respect. Here we focus on results from a single month (July 2006), which was extremely hot and had a high potential for convection (Hohenegger et al. 2008). Note that several additional case studies (not shown) reveal that these results are not dependent on the time period or on the domain under investigation.
Figure 11 displays the analysis for July 2006, with a focus on the Alpine area (similarly as in Hohenegger et al. 2009). The mean diurnal cycle of precipitation reveals a striking peak due to afternoon convection (see right panels). Again, the comparison of CTL with PWP and FCAP suggests a positive SM-precipitation feedback. Interestingly, the convective activity does not seem to linearly increase with the available soil moisture. Though the SM of CTL lies in between PWP and FCAP, the diurnal cycle of precipitation in CTL is only slightly larger than in PWP but much weaker than in FCAP. This can be understood by the increased latent heat flux in FCAP, and by the parametrisation of convection according to Tiedtke (1989). The latter is indeed highly non-linear and its strength depends on the atmospheric moisture flux convergence, thus on LE, and its triggering on the stability at the condensation level of a lifted air parcel.
Left panels Time series of precipitation (mm/3 h) and soil moisture (cm, insets model level 1–5 ≈ top 50 cm) averaged over the Alpine area for July 2006. The bold lines at the top denote episodes when the convective precipitation is larger than >80% of the total precipitation. Right panels As in left panels but for monthly mean diurnal cycle of precipitation (mm/3 h). Top rows display CTL, PWP and FCAP. Bottom rows are for CTL, SSV, ISV and IAV
The lower panels of Fig. 11 display the same analyses but for the SSV, ISV and IAV experiments. For this particular month the absolute value of SM in the experiments is continously increasing from SSV to IAV. Consistent with this and with the positive SM-precipitation feedback identified in this model setup, there is a continous increase in convection from SSV to IAV compared to CTL as shown by their mean diurnal cycles of precipitation. Another interesting feature is the fact that despite identical large-scale forcing in all experiments, not all single convection events of this month exhibit a positive feedback (holds for all experiments). Note that these results may be dependent on the model configuration (parametrisations, spatial resolution, etc.). For instance Hohenegger et al. (2009) found diverging SM-precipitation feedbacks with changes in resolution and in the representation of convection in another version of the CLM model (version 4.0, see Sect. 2.1). Moreover, also land surface parametrisations can display a range of sensitivity of evapotranspiration to SM, and large variations in soil parameters (e.g. Seneviratne et al. 2002, 2006a; Koster et al. 2004; Pitman et al. 2009).
6 Trends in climate extremes and their link to soil moisture
In this section we investigate trends in summer climate over the period 1959–2006 in the conducted experiments. Of particular interest is the question of whether changes in soil moisture characteristics may have any influence on these trends. Using the performed CLM experiments with and without prescribed SM, this can be easily assessed. We do not perform this analysis for all diagnostics listed in Table 2, but restrict it to the PDFs of daily precipitation and T max as described by their mean, inter-quartile range (iqr) and perc95. Moreover, we also analyse trends of minimum daily temperature (T min , not shown), diurnal temperature range (DTR), cloud cover and SM. This can be investigated using the non-parametric Mann-Kendall tau test that is based on the Theil-Sen’s trend estimate (robust slope estimator, details in “Appendix 2”). It is a robust, rank-based test for trends (e.g. Lettenmaier et al. 1994), and we apply it here to the 48 JJA values (1959–2006) to avoid issues related to serial correlation. Finally, we also apply a non-stationary extreme value analysis to investigate if the parameters of the GEV of seasonal maxima of daily precipitation and T max have a linear trend (details in “Appendix 2”, likelihood ratio test).
The analysis reveals that the trends are different for simulations with (CTL, SSV, ISV) and without (IAV, PWP, FCAP) SM trends, respectively. However, since there are no substantial differences (not shown) between CTL, SSV and ISV, respectively IAV, PWP and FCAP, we only discuss here the trends for CTL and IAV.
We distinguish here two periods corresponding to the ‘global-dimming/global-brightening’ phases (e.g. Wild et al. 2004; Makowski et al. 2009): 1959–1980 (1st period) and 1981–2006 (2nd period). Figure 12 shows that there is a striking temporal variation in the Theil-Sen’s trend estimates for the mean of daily T max between the 1st and 2nd periods. For CTL there is a negative trend for the 1st period over the whole of Europe, and a positive trend for the 2nd period. For IAV there is a tendency for smaller negative and positive trends for the 1st and 2nd period, respectively (the numbers in the lower right corner denote the area-weighted fraction of land points with statistically significant trends according to the Mann-Kendall tau test, or likelihood ratio test for μ, at the 10% level).
Linear trends as expressed by Theil-Sen’s trend estimate for the 1st (1959–1980) and 2nd (1981–2006) summer periods. From left to right: CTL and IAV-CTL for the 1st period; CTL and IAV-CTL for the 2nd period. From top to bottom: mean daily T max (K/y), DTR (K/y), location parameter μ of GEV from a non-stationary extreme value analysis for daily T max (K/y) and for daily precipitation (mmd−1/y), total cloud cover (%/y), and soil moisture (m/y) (model level 1–7 ≈ top 1.9 m)
The corresponding trends for T min exhibit similar spatial and temporal patterns but are weaker (not shown). Moreover, the differences between CTL and IAV are substantially smaller. Hence, SM (trends) unequally affect T max and T min (trends) as also suggested by e.g. Zhang et al. (2009). The DTR trends (see Fig. 12) are a consequence thereof, and again display similar spatial and temporal patterns as the T max and T min trends.
As a measure of trends of extremes we also investigate the Theil-Sen trend estimates for the parameters of the GEV (only location μ and scale σ) and for the tails of the PDFs of daily T max as given by perc95. The trend patterns of μ and perc95 are the same as for the mean of T max , but there is a tendency for larger positive trends mainly over Eastern Europe (see Fig. 12 for μ). Moreover, the effect of SM trends is particularly strong for the trends in temperature extremes at least for the 2nd period. On the contrary trends of σ are hardly significant (not shown). As a measure of trends in the width of the PDFs of daily T max we use the Theil-Sen estimate for iqr, which again exhibits similar trend patterns, except for Northern Africa and the Iberian Peninsula (hardly significant, hence not shown).
The pattern of the Theil-Sen’s trend estimates for the precipitation extreme diagnostics are in line with those for temperature, though much noisier and hardly significant (μ is exemplarily shown in Fig. 12). Again, indices describing the upper tail of the precipitation PDFs exhibit the strongest positive (1st period) and negative (2nd period) trends, but also trends in the width of the PDFs are similar to those of the extreme diagnostics. Among the different CLM experiments the trend patterns look similar except for FCAP with smaller negative trends in Southern Europe (2nd period, likely due to the lack of SM induced summer drying), whereas there are generally slightly decreased positive (1st) and negative (2nd period) trends for freq for those experiments without SM trends (not shown). The trends in precipitation extreme diagnostics pinpoint to similar results for current climate (2nd period) as obtained in the multi-model analysis of Frei et al. (2006) (also including an earlier version of CLM), analysing projections in extreme precipitation for 2071–2100 compared to 1961–1990: a Southern European decrease and Northern European increase.
As mentioned above, the temporal characteristics of the trends suggest a link with the ‘global-dimming/global-brightening’ phases. The switch from the dimming to the brightening phase, occured during the early 80s likely due to a decline in aerosol emissions. This resulted mostly in changes in radiation, but one should keep in mind the numerous possible feedbacks, e.g. through impacts on evapotranspiration (Teuling et al. 2009), circulation patterns (e.g. Rotstayn and Lohmann 2002), and/or cloud and precipitation formation (Rosenfeld et al. 2008). Note that in CLM as well as in the boundary conditions driving the experiments (ERA40, ECMWF operational analysis), aerosol concentrations are constant over time (climatology). Therefore, either trends unrelated to aerosol concentrations, or associated with indirect (and non-local) effects of the latter, have to be responsible for the simulated trends in daily T max and precipitation in CLM. We cannot clearly disentangle both effects in our simulations. But note that indirect (and non-local) effects of aerosols (changes in circulation patterns or atmospheric moisture content, possibly leading to changes in cloud cover) could indeed be captured by the reanalysis/operational analysis datasets used as boundary conditions in our simulations, thanks to the assimilation of radiosonde measurements (see also Hirschi and Seneviratne 2010). Therefore, we also investigate the trends in CLM total cloud cover in Fig. 12. They show the same spatial as well as temporal patterns (with an increase in the 1st period and a decrease thereafter) as the trends in daily T max and precipitation. Note that the SM trend patterns (both spatial and temporal) are similar to those of the cloud cover. Since cloud cover and SM interact with one another, it is difficult to assess their respective independent contributions to the trends. However, by looking at those simulations without trends in SM, one finds a small trend reduction in particular for μ of T max (but not for μ of precipitation). Therefore, we conclude that in CLM the trends of daily T max , of DTR and of freq are mainly due to trends in cloud cover caused by the large-scale forcing (circulation patterns, as well as temperature and relative humidity of incoming air at the domain boundaries), and that SM has an amplifying effect.
Note that inhomogeneities (e.g. associated with changes in the global observing system in 1979 or the change from reanalysis to operational analysis in 2002) present in the boundary data can possibly blur the identified trends (e.g. Bengtsson et al. 2004; Seneviratne et al. 2004), although, as discussed in Sect. 7, the overall moisture trend in the boundary data agrees with observations.
7 Biases of CTL
In this section, we briefly assess the biases of the CLM reference simulation (CTL) with respect to observations (E-OBS for T max and precipitation; ERA40 reanalysis for cloud cover) and in comparison with the ERA40-driven ENSEMBLES RCMs (E-RCMs, see Sect. 2.2) for the PRUDENCE subdomain mean values. We only perform the corresponding analysis for the extremes and trends, whereas for the mean climate and land surface exchanges, or for profiles, we refer the reader to Jaeger et al. (2008, 2009), or Brockhaus et al. (2008), respectively.
If we compare the daily T max diagnostics of CTL with those of E-OBS, we identify the following biases (black dots): perc95 (Fig. 13 a) and ret50 (not shown) are both overestimated in Southern and particularly in Eastern Europe, whereas in Central and Northern Europe they are slightly underestimated. Therefore, the North-South and East-West gradients mentioned in Sect. 4.1.1 are rather overestimated in CTL. Note that for the E-RCMs (boxplots) the magnitude and the pattern of the bias is similar as in CTL, and that the latter was already found in the PRUDENCE RCMs (Kjellström et al. 2007). While in the E-RCMs the biases of hwdi max (Fig. 13b) and hwdi mean (not shown) are similar to those of perc95, there are smaller biases in CTL with a noisy pattern of over- and underestimation across the whole European continent. For the precipitation extremes in CTL, we find an overestimation of perc95 (Fig. 13c) and of freq (Fig. 13d), which is similar in the E-RCMs and in another CLM version (4.0, Brockhaus et al. 2010).
Boxplots (e.g. Wilks 2006) showing the bias of the ERA40-driven ENSEMBLES RCMs (25 km simulations) with respect to E-OBS (for T max and precipitation) and to ERA40 (for total cloud cover). The black dots denote the corresponding bias for CTL. The analysis is done for the mean values of the PRUDENCE subdomains: Britain (BI), Iberian Peninsula (IP), France (FR), Mid-Europe (ME), Scandinavia (SC), Alps (AL), Mediterranean (MD), and Eastern Europe (EA). Top row shows (from left to right): bias of the indices a perc95 (T max ), b hwdi max , c perc95 (daily precipitation, > 1 mm/d), and d freq (>1 mm/d) for the summer period 1961–2000. Bottom row (from left to right): bias of trends in e mean (T max ), f μ(T max ), g μ (daily precipitation), and h total cloud cover for the considered time periods (1961–1980, left values; 1981–2000, right values)
The bottom panels of Fig. 13 display biases in trends of several variables for two periods similar to those considered in Sect. 6 (1961–1980; 1981–2000). The analysis is based on the Theil-Sen’s trend estimates for the mean of daily T max (Fig. 13 e), for the GEV location parameter μ (both for T max and daily precipitation), and for the total cloud cover. It is striking that both in CTL and the E-RCMs the trend in mean daily T max is underestimated for both periods (too strongly negative for the 1st period; too small for the 2nd period). For the trends in extremes of T max as given by μ (Fig. 13f) there is a tendency for an underestimation for the 1st period and an overestimation for the 2nd period, again both in CTL and in the E-RCMs, whereas for the trends in extremes of precipitation (Fig. 13g) there is hardly any spatial or temporal structure. The overall CTL cloud trend (first increasing, then decreasing) is in line with those of the boundary conditions driving the experiments (ERA40, ECMWF operational analysis, not shown) as well as with surface observations for the 1971–1996 period (Warren et al. 2007). There is a slight tendency in the total cloud cover trend of the E-RCMs (but less so in CTL) for an underestimation in the 1st and an overestimation in the 2nd period (Fig. 13h). Finally, note that Makowski et al. (2009) found generally weak correlations between modeled and observed summer DTR trends in the E-RCMs, but much higher correlations for CLM (our CLM simulation corresponds to ETHZ44 in Table 6 of their study).
In summary, the biases of extremes and trends of the CLM simulations (CTL) used for this study are comparable to those of current state-of-the-art RCMs. This appears to be independent of resolution since the analysed E-RCMs have a horizontal resolution of 25 km compared to 50 km for CTL.
8 Conclusions
This study investigates the role of soil moisture variability on different time scales as well as of extreme values of soil moisture for the European summer climate. For this aim, a control simulation and a set of sensitivity experiments with prescribed SM conditions are performed with the regional climate model CLM over the time period 1958–2006, using ECWMF reanalysis and operational analysis data as boundary conditions. We focus in the analysis on the role of SM for temperature and precipitation extremes, as well as on trends thereof. Some of the results are also evaluated with the E-OBS observations and the ERA40 reanalysis dataset, and the accuracy of the CTL simulation is compared with that of other state-of-the-art RCMs. The main results of this study are as follows:
-
1.
As to be expected, the mean summer climate is not strongly affected by temporal SM variability, as the average SM seasonal evolution stays the same (SSV, ISV, IAV). Nonetheless, asymmetric effects on mean climate can be identified from these simulations (in particular IAV), which suggest a higher impact of soil moisture in dry conditions in Europe. Furthermore, prescribed extreme values of SM (PWP, FCAP) exhibit a strong impact on mean climate, with wet soils (FCAP) leading to an increase in LE and a decrease in H. This causes a shallower, moister and colder PBL with increased total cloud cover and, consequently, decreased SW net and increased LW net (opposite behaviour for dry soils, i.e. PWP). The net effect on R net , however, is of same sign for the wet and dry simulations (decrease) and is suggestive of asymmetric effects of SM anomalies. This is in contrast with results of previous studies regarding SM-precipitation feedbacks (Eltahir 1998; Schär et al. 1999), which suggested a possible increase of R net with wetter conditions. Overall, wet soils cause a decrease in T max , mainly in arid areas, and dry soils an increase in T max , mainly in humid areas. Moreover, CLM exhibits a positive SM-precipitation feedback in the employed model version (with 50 km horizontal resolution and the Tiedtke (1989) convection scheme based on moisture-convergence closure).
-
2.
Temperature extremes, as investigated by climate extreme indices, PDFs and extreme value analysis, are strongly affected by the absolute value and to a smaller extent also by changes in the temporal variability of SM. This is mainly due to intraseasonal as well as interannual SM variability, with largest impacts over Scandinavia and Central Europe. Our results also suggest that the reduction of heat waves by 50–80% due to SM effects identified by Fischer et al. (2007a) is not only due to interannual variability of SM but partly also to intraseasonal variability. In addition, SM memory effects are found to be important for the intrinsic persistence of hot days (see also Lorenz et al. 2010). Furthermore, the effect of SM on temperature is asymmetric with strongest impacts on temperature maxima.
-
3.
In contrast to the results for temperature, our results suggest that precipitation extremes are not significantly affected by temporal SM variability. Significant impacts are only found for the extreme experiments (PWP, FCAP) where the wet-day frequency and consequently the absolute mean summer daily precipitation and 5dmax, all have larger values in the wet case due to increased frequency of days with convective precipitation. However, the wet-day characteristics, as expressed by e.g. int and perc95, are similar for all experiments.
-
4.
Trends of daily T max and precipitation, as well as of extremes thereof, follow the ‘global-dimming/global-brightening’ trends in radiation in the experiments. In CLM, the trends are mostly due to trends in cloud cover, whereas SM acts as an amplifier. This is the case in the experiments, although they do not include directly observed trends in aerosols, but only possible indirect constraints through the boundary conditions. Trends in the extremes of T max are particularly affected by SM trends. The latter result suggests that the increasing trend in temperature extremes is partly associated with a drying trend in SM in the simulations.
-
5.
Trends of daily T min are similar to those of T max but less affected by SM trends and therefore smaller. Hence, trends in DTR appear partly due to trends in SM (through its impact on T max ).
In conclusion, this analysis has shown that soil moisture-climate interactions can have a significant effect on temperature as well as partly on precipitation extremes for the European summer climate. Moreover, most of the tendencies in summer climate characteristics projected for the 21st century, with an increase in temperature all over Europe (e.g. Kjellström et al. 2007) and a Southern European decrease and Northern European increase in precipitation extremes (Frei et al. 2006), appear consistent with simulated trends for the past decades in CTL. These seem to be at least partly linked to SM trends in the simulations. In order to properly evaluate the model dependency of our results, it would be necessary to repeat the analysis using different RCMs in a multi-model framework.
References
Alexander LV et al (2006) Global observed changes in daily climate extremes of temperature and precipitation. J Geophys Res 111:D05109. doi:10.1029/2005JD006290
Beljaars ACM, Viterbo P, Miller MJ, Betts AK (1996) The anomalous rainfall over the United States during July 1993: sensitivity to land surface parameterization and soil moisture. Mon Weather Rev 124:362–383
Bengtsson L, Hagemann S, Hodges KI (2004) Can climate trends be calculated from reanalysis data? J Geophys Res 109:D11111. doi:10.1029/2004JD004536
Black E, Blackburn M, Harrison G, Hoskins B, Methven J (2004) Factors contributing to the summer 2003 European heatwave. Weather 59:217–223
Black E, Sutton R (2006) The influence of oceanic conditions on the hot European summer of 2003. Clim Dynam 28:53–66
Brockhaus P, Lüthi D, Schär C (2008) Aspects of the diurnal cycle in a regional climate model. Meteorol Z 17:433–443
Brockhaus P, Bechthold P, Fuhrer O, Lüthi D, Schär C (2010) The ECMWF IFS convection scheme applied to the COSMO limited-area model. Q J R Meteorol Soc (submitted)
Brown SJ, Caesar J, Ferro CAT (2008) Global changes in extreme daily temperature since 1950. J Geophys Res 113:D05115. doi:10.1029/2006JD008091
Christensen JH, Christensen OB (2003) Severe summertime flooding in Europe. Nature 421:805–806
Christensen JH, Christensen OB (2007) A summary of the PRUDENCE model projections of changes in European climate during this century. Clim Change. doi:10.1007/s10584-006-9210-7
Ciais P et al (2005) Europe-wide reduction in primary productivity caused by the heat and drought in 2003. Nature 437:529–533
Coelho CAS, Ferro CAT, Stephenson DB, Steinskog DJ (2008) Methods for exploring spatial and temporal variability of extreme events in climate data. J Climate 21:2072–2092
Coles SG (2001) An introduction to statistical modeling of extreme values. Springer Series in Statistics, Springer, 224
Conil S, Douville H, Tyteca S (2007) The relative influence of soil moisture and SST in climate predictability explored within ensembles of AMIP type experiments. Clim Dynam 28:125–145
Della-Marta PM, Haylock MR, Luterbacher J, Wanner H (2007) Doubled length of western European summer heat waves since 1880. J Geophys Res 112:D15103. doi:10.1029/2007JD008510
Dickinson RE (1984) Modeling evapotranspiration for the three-dimensional global climate models. In: Hansons JE, Takahashi T (eds) Climate Processes and Climate Sensitivity, Geophys Monogr Ser, vol 29. AGU, Washington, DC, pp 58–72
Ek MB, Holtslag AAM (2004) Influence of soil moisture on boundary layer cloud development. J Hydrometeor 5:86–99
Eltahir EAB (1998) A soil moisture–rainfall feedback mechanism, 1. Theory and observations. Water Resour Res 34:765–776
Fink A, Brücher T, Krüger A, Leckebusch G, Pinto J, Ulbrich U (2004) The 2003 European summer heat waves and drought–synoptic diagnosis and impacts. Weather 59:209–216
Fischer EM, Seneviratne SI, Lüthi D, Schär C (2007a) Contribution of land–atmosphere coupling to recent European summer heat waves. Geophys Res Lett 34:L06707. doi:10.1029/2006GL029068
Fischer EM, Seneviratne SI, Vidale PL, Lüthi D, Schär C (2007b) Soil moisture–atmosphere interactions during the 2003 European summer heat wave. J Climate 20:5081–5099
Frei C, Schöll R, Fukutome S, Schmidli J, Vidale PL (2006) Future change of precipitation extremes in Europe: intercomparison of scenarios from regional climate models. J Geophys Res 111:D06105. doi:10.1029/2005JD005965
Haylock MR, Hofstra N, Klein Tank AMG, Klok EJ, Jones PD, New M (2008) A European daily high-resolution gridded dataset of surface temperature and precipitation. J Geophys Res 113:D20119. doi:10.1029/2008JD10201
Heck P, Zanetti A, Enz R, Green J, Suter S (2004) Natural catastrophes and man-made disasters in 2003. Sigma Report No. 1/2004
Hirschi M, Seneviratne SI (2010) Intra-annual link of spring and autumn precipitation over France. Clim Dynam. doi:10.1007/s00382-009-0734-1
Hohenegger C, Brockhaus P, Schär C (2008) Towards climate simulation at cloud resolving scales. Meteorol Z 17:383–394
Hohenegger C, Brockhaus P, Bretherton C, Schär C (2009) The soil moisture–precipitation feedback in simulations with explicit and parameterized convection. J Climate 22:50035020
Jaeger EB, Anders I, Lüthi D, Rockel B, Schär C, Seneviratne SI (2008) Analysis of ERA40-driven CLM simulations for Europe. Meteorol Z 17:349–367
Jaeger EB, Stöckli R, Seneviratne SI (2009) Analysis of planetary boundary layer fluxes and land–atmosphere coupling in the Regional Climate Model CLM. J Geophys Res 114:D17106. doi:10.1029/2008JD011658
Kharin VV, Zwiers FW (2000) Changes in the extremes in an ensemble of transient climate simulation with a coupled atmosphere–ocean GCM. J Climate 13:3760–3788
Kharin VV, Zwiers FW (2005) Estimating extremes in transient climate change simulations. J Climate 18:1156–1173
Kjellström E, Bärring L, Jacob D, Jones R, Lenderink G, Schär C (2007) Modelling daily temperature extremes: recent climate and future changes over Europe. Clim Change 81:249–265
Klein Tank AMG et al (2002) Daily dataset of 20th-century surface air temperature and precipitation series for the European Climate Assessment. Int J Climatol 22:1441–1453
Klein Tank AMG, Können GP (2003) Trends in indices of daily temperature and precipitation extremes in Europe, 1946–99. J Climate 16:3665–3680
Koster R, Suarez M (1995) Relative contributions of land and ocean processes to precipitation variability. J Geophys Res 100(D7):13775–13790
Koster RD et al (2004) Regions of strong coupling between soil moisture and precipitation. Science 305:1138–1140
Larsen J (2003) Record heat wave in Europe takes 35,000 lives. Earth Policy Institute
Laurent C, Parey S (2007) Estimation of 100-year-return-period temperatures in France in a non-stationary climate: results from observations and IPCC scenarios. Global and Planetary Change 57:177–188
Lettenmaier DP, Wood EF, Wallis JR (1994) Hydro-climatological trends in the Continental United States, 1948–88. J Climate 7:586607
Lorenz R, Jaeger EB, Seneviratne SI (2010) Persistence of heat waves and its link to soil moisture memory. Geophys Res Lett (revised)
Makowski K, Jaeger EB, Chiacchio M, Wild M, Ewen T, Ohmura A (2009) On the relationship between diurnal temperature range and surface solar radiation in Europe. J Geophys Res 114:D00D07. doi:10.1029/2008JD011104
Martins ES, Stedinger JR (2000) Generalized maximum-likelihood generalized extreme-value quantile estimators for hydrologic data. Water Resour Res 36(3):737–744
Martius O, Zenklusen E, Schwierz C, Davies HC (2006) Episodes of Alpine heavy precipitation with an overlying elongated stratospheric intrusion: a climatol. Int J Clim 26:1149–1164
Meehl GA, Tebaldi C (2004) More Intense, more Frequent, and longer lasting heat waves in the 21st century. Science 305:994–997
Pal JS, Eltahir EAB (2002) Teleconnections of soil moisture and rainfall during the 1993 midwest summer flood. Geophys Res Lett 29:1865. doi:10.1029/2002GL014815
Pal JS, Giorgi F, Bi X (2004) Consistency of recent European summer precipitation trends and extremes with future regional climate projections. Geophys Res Lett 31:L13202. doi:10.1029/2004GL019836
Perkins SE, Pitman AJ, Holbrook NJ, McAneney J (2007) Evaluation of the AR4 climate models’ simulated daily maximum temperature, minimum temperature, and precipitation over Australia using probability density functions. J Climate 20:4356–4376
Pitman AJ et al (2009) Uncertainties in climate responses to past land cover change: First results from the LUCID intercomparison study. Geophys Res Lett 36:L14814. doi:10.1029/2009GL039076
Raschendorfer M (2001) The new turbulence parametrization of LM. COSMO newsletter, 1:90–98. http://www.cosmo-model.org
Ritter B, Geleyn JF (1992) A comprehensive radiation scheme of numerical weather prediction with potential application to climate simulations. Mon Wea Rev 120:303–325
Rosenfeld D, Lohmann U, Raga GB, O’Dowd CD, Kulmala M, Fuzzi S, Reissell A, Andreae MO (2008) Flood or drought: how do aerosols affect precipitation? Science 321:1309–1313
Rotstayn LD, Lohmann U (2002) Tropical rainfall trends and the indirect aerosol effect. J Climate 15:2103–2116
Rowell DP, Jones RG (2006) Causes and uncertainty of future summer drying over Europe. Clim Dynam 27:281–299. doi:10.1007/s00382-006-0125-9
Schär C, Lüthi D, Beyerle U, Heise E (1999) The Soil-precipitation feedback: a process study with a Regional Climate Model. J Climate 12:722–741
Schär C, Vidale PL, Lüthi D, Frei C, Häberli C, Liniger MA, Appenzeller C (2004) The role of increasing temperature variability in European summer heatwaves. Nature 427:332–336
Schmidli J, Frei C (2005) Trends of heavy precipitation and wet and dry spells in Switzerland during the 20th century. Int J Climatol 25:753771
Schrodin R, Heise E (2002) A new multi-layer soilmodel. COSMO newsletter 2:149–151. http://www.cosmo-model.org
Sen PK (1968) Estimates of the regression coefficient based on Kendalls Tau. J Am Stat Assoc 63:1379–1389
Seneviratne SI, Pal JS, Eltahir EAB, Schär C (2002) Summer dryness in a warmer climate: a process study with a regional climate model. Clim Dynam 20:69–85
Seneviratne SI, Viterbo P, Lüthi D, Schär C (2004) Inferring changes in terrestrial water storage using ERA-40 reanalysis data: the Mississippi River basin. J Climate 17:2039–2057
Seneviratne SI, Koster RD, Guo Z, Dirmeyer PA, Kowalczyk E, Lawrence D, Liu P, Lu C-H, Mocko D, Oleson KW, Verseghy D (2006a) Soil moisture memory in AGCM simulations: analysis of global land–atmosphere coupling experiment (GLACE) data. J Hydrometeor 7:1090–1112
Seneviratne SI, Lüthi D, Litschi M, Schär C (2006b) Land–atmosphere coupling and climate change in Europe. Nature 443:205–209
Seneviratne SI, Corti T, Davin EL, Hirschi M, Jaeger EB, Lehner I, Orlowsky B, Teuling AJ (2010) Soil moisture-climate interactions in a changing climate: a review. Earth Sci Rev (in press)
Steppeler J, Dom G, Schättler U, Bitzer HW, Gassmann A, Damrath U, Gregoric G (2003) Meso-gamma scale forecasts using the nonhydrostatic model LM. Meteorol Atmos Phys 82:75–96
Tebaldi C, Hayhoe K, Arblaster JM, Meehl GA (2006) Going to the extremes; an intercomparison of model-simulated historical and futre changes in extreme events. Clim Change 79:185–211
Teuling AJ, Hirschi M, Ohmura A, Wild M, Reichstein M, Ciais P, Buchmann N, Ammann C, Montagnani L, Richardson AD, Wohlfahrt G, Seneviratne SI (2009) A regional perspective on trends in continental evaporation. Geophys Res Lett 36:L02404. doi:10.1029/2008GL036584
Tiedtke M (1989) A comprehensive mass flux scheme for cumulus parameterization in large-scale models. Mon Wea Rev 117:1779–1800
Uppala SM et al (2005) The ERA-40 reanalysis. Q J R Meteorol Soc 131:2961–3012
Vidale PL, Lüthi D, Wegmann R, Schär C (2007) European summer climate variability in a heterogeneous multi-model ensemble. Clim Change 81:209–232
Warren SG, Eastman RM, Hahn CJ (2007) A survey of changes in cloud cover and cloud types over land from surface observations, 197196. J Climate 20:717–738
Wild M, Gilgen H, Roesch A, Ohmura A, Long C, Dutton E, Forgan B, Kallis A, Russak V, Tsvetkov A (2004) From dimming to brightening: decadal changes in solar radiation at the Earth’s surface. Science 308:847–850
Wilks DS (1997) Resampling hypothesis tests for autocorrelated fields. J Climate 10:65–82
Wilks DS (2006) Statistical methods in the atmospheric sciences. Elsevier, New York, p 627
Will A, Baldauf M, Rockel B, Seifert A (2010) Physics and dynamics of the CLM. Meteorolog Z (submitted)
Zhang J, Wang WC, Wu L (2009) Land–atmosphere coupling and diurnal temperature range over the contiguous United States. Geophys Res Lett 36:L06706. doi:10.1029/2009GL037505
Zwiers FW, Kharin VV (1998) Changes in the extremes of the climate simulated by CCC GCM2 under CO2 doubling. J Climate 11:2200–2222
Acknowledgements
This research was supported through the EU-FP6 project CECILIA (contract number 037005) and ETH Zurich. The simulations have been conducted at the Swiss National Supercomputing Centre (CSCS). We are indebted to the COSMO and CLM communities, as well as to MeteoSwiss and ECMWF, for providing access to and support for the CLM and the ERA40 reanalysis/ECMWF operational analysis, respectively. We are particularly indebted to Johanna Nes˘lehová and the Seminar for Statistics (ETH) for statistical advice, to Martin Hirschi and Peter Brockhaus for discussions, to Daniel Lüthi for technical support, and to Christoph Frei for sharing his R package for the stationary extreme value analysis. Also, we would like to acknowledge the E-OBS dataset from the EU-FP6 project ENSEMBLES (http://www.ensembles-eu.org) and the data providers in the ECA&D project (http://eca.knmi.nl). The ENSEMBLES data used in this work was funded by the EU FP6 Integrated Project ENSEMBLES (contract number 505539).
Open Access
This article is distributed under the terms of the Creative Commons Attribution Noncommercial License which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix 1: Digital filtering of soil moisture
For the prescribed SM experiments SSV, ISV and IAV a zero-phase digital filtering is applied to compute the SM evolution for each grid point and soil layer separately. Therefore the input data (SM from CTL) is processed in both the forward and reverse directions in order to get precisely zero-phase distortion and a minimization of start-up and ending transients. We use a digital Butterworth lowpass filter of tenth order. Butterworth filters are characterized by a magnitude response that is maximally flat in the passband and monotonic overall. They sacrifice rolloff steepness for monotonicity in the pass- and stopbands. For further details see the Matlab homepage (http://www.mathworks.com).
Appendix 2: Tests for statistical significance
Here we briefly list the different statistical tests that have been applied in this study:
Two-sided Kolmogorov–Smirnov test: Tests if two samples come from the same continuous distribution (H o ), against the alternative that they do not come from the same distribution (H a ). The test statistic is: max(|F1(x) − F2(x)|), where F1(x) and F2(x) are the empirical distribution functions of the two samples. This test has been applied to Figs. 2, 4, 5, 6, 7 and 8 (as well as to the figures of the supplementary material).
Non-parametric bootstrap tests: To test if the return values of two different experiments are significantly different, we calculate 100 bootstrap samples. Then, for each pair of the two samples we compute the difference to estimate the distribution of the difference between the two return values. Based on the quantiles of this distribution it can be tested if it is significantly different from zero (applied in Fig. 4 and 6). The same procedure has been applied to test the statistical quantities of the daily precipitation and T max PDFs listed in the tables of the supplementary material (using 1000 samples).
Mann–Kendall tau trend test: It is a non-parametric test for trends with H o : time series values are i.i.d and H a : there is a monotonic (not necessarily linear) trend. It is based on a robust non-parametric slope estimator called Theil-Sen (Sen 1968) that is the median of slopes between all possible data pairs of the time series X i (with i = 1, ..., n): \(\beta_{TS}=\mathop{\hbox{median}}\limits_{i<k}((x_k-x_i)/(k-i)).\) It has been used for Fig. 12.
Likelihood ratio test: Tests if two nested models are significantly different from each other. In this study, it has been applied to the non-parametric GEV models (Fig. 12) to assess if model M1 (e.g. with a trend in μ) is significantly better than the simpler model M0 (where k components are 0, e.g. no trend in μ), using the deviance statistic: D = 2 {l1(M1) − l0(M0)} > cα, where l0(M0) and l1(M1) are the maximized log-likelihoods under models M0 and M1 respectively, and cα denotes the (1 − α) quantile of the \(\chi_{k}^{2}\) distribution (Coles 2001).
Rights and permissions
Open Access This is an open access article distributed under the terms of the Creative Commons Attribution Noncommercial License (https://creativecommons.org/licenses/by-nc/2.0), which permits any noncommercial use, distribution, and reproduction in any medium, provided the original author(s) and source are credited.
About this article
Cite this article
Jaeger, E.B., Seneviratne, S.I. Impact of soil moisture–atmosphere coupling on European climate extremes and trends in a regional climate model. Clim Dyn 36, 1919–1939 (2011). https://doi.org/10.1007/s00382-010-0780-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00382-010-0780-8