Delay differential systems for tick population dynamics

Abstract

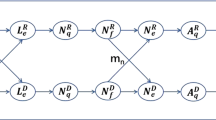
Ticks play a critical role as vectors in the transmission and spread of Lyme disease, an emerging infectious disease which can cause severe illness in humans or animals. To understand the transmission dynamics of Lyme disease and other tick-borne diseases, it is necessary to investigate the population dynamics of ticks. Here, we formulate a system of delay differential equations which models the stage structure of the tick population. Temperature can alter the length of time delays in each developmental stage, and so the time delays can vary geographically (and seasonally which we do not consider). We define the basic reproduction number ${\mathcal R}_0$ of stage structured tick populations. The tick population is uniformly persistent if ${\mathcal R}_0>1$ and dies out if ${\mathcal R}_0<1$. We present sufficient conditions under which the unique positive equilibrium point is globally asymptotically stable. In general, the positive equilibrium can be unstable and the system show oscillatory behavior. These oscillations are primarily due to negative feedback within the tick system, but can be enhanced by the time delays of the different developmental stages.

Appendices

Appendix 1: Proofs for Sect. 4

Proof of Theorem 4.1

Consider system (3.3) with nonnegative initial data (3.8) and birth function $G(s)$ in (3.4). Any solution of (3.3) is nonnegative, becomes strictly positive at some time, and remains positive thereafter.

Without loss of generality, we assume that the number of adult ticks $x_{30}(\theta )$ is not identically zero for $\theta \in [-\tau _3,\ 0]$. There exists $\theta ^*\in (-\tau _3,\ 0)$ such that $x_{30}(\theta ^*)>0$. By the continuity of the function, there exists a neighborhood $(\theta ^*-\delta ,\theta ^*+\delta )$ such that $x_{30}(\theta )>0$, where $\delta$ is a small positive number. For any $t^*\in [0,\ \tau _3]$ and $t^*>\theta ^*+\tau _3+\delta$,

$$\begin{aligned} x_1(t^*)&= \int _0^{t^*}\gamma _3p_3 e^{-\eta _1(s-t^*)}G(x_{30}(s - \tau _3))\mathrm {d}s+x_{10}(0) e^{-\eta _1t^*}\\&> \int _{\theta ^*-\delta }^{\theta ^*+\delta }\gamma _3p_3 e^{-\eta _1(s-t^*)}G(x_{30} (s - \tau _3))\mathrm {d}s \; >0. \nonumber \end{aligned}$$

(8.1)

After time $t^*$, $x_1(t)$ can never become zero again since

$$\begin{aligned} x_1'(t)>- \eta _1 x_1 (t) \quad \mathrm {and}\quad x_1(t)\geqslant x_1(t^*)e^{-\eta _1(t-t^*)}>0. \end{aligned}$$

If $\theta ^*=-\tau _3$ or $0$, we can modify the proof a little bit and take the neighborhood $(-\tau _3,-\tau _3+\delta )$ or $(-\delta ,0)$. Our proof still works. Similarly we can prove that $x_2(t)$ and $x_3(t)$ are strictly positive at some $\bar{t}>0$ and remain strictly positive thereafter.

Let $T> 0$ be arbitrary. From the integral equation for $x_1$ like in (8.1), we have that

$$\begin{aligned} \sup _{-\tau _1 \le t \le T} x_1(t) \le \sup _{-\tau _1 \le t \le 0} x_{10}(t) + \frac{\gamma _3 p_3}{\eta _1} \sup _{-\tau _3 \le t \le T} G(x_3(t)). \end{aligned}$$

After integrating the differential equation for $x_2$,

$$\begin{aligned}&\sup _{-\tau _2 \le t \le T} x_2(t) \le \sup _{-\tau _2 \le t \le 0} x_{20}(t) + \frac{\gamma _1 p_1}{\eta _2} \sup _{-\tau _1 \le t \le T} x_1(t)\\ \le&\sup _{-\tau _2 \le t \le 0} x_{20}(t) + \frac{\gamma _1 p_1}{\eta _2}\sup _{-\tau _1 \le t \le 0} x_{10}(t) + \frac{\gamma _1 p_1}{\eta _2}\frac{\gamma _3 p_3}{\eta _1} \sup _{-\tau _3 \le t \le T} G(x_3(t)). \end{aligned}$$

We integrate the differential equation for $x_3$,

$$\begin{aligned}&\sup _{-\tau _3 \le t \le T} x_3(t) \le \sup _{-\tau _3 \le t \le 0} x_{30}(t) + \frac{\gamma _2 p_2}{\eta _3} \sup _{-\tau _2 \le t \le T} x_2(t)\nonumber \\ \le&c_3 + \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \sup _{-\tau _3 \le t \le T} G(x_3(t)) \end{aligned}$$

(8.2)

with

$$\begin{aligned} c_3 = \sup _{-\tau _3 \le t \le 0} x_{30}(t) + \frac{\gamma _2 p_2}{\eta _3} \sup _{-\tau _2 \le t \le 0} x_{20}(t) + \frac{\gamma _2 p_2}{\eta _3}\frac{\gamma _1 p_1}{\eta _2} \sup _{-\tau _1 \le t \le 0} x_{10}(t) . \end{aligned}$$

(8.3)

Assume that ${\mathcal R}_\infty < 1$ and let $x >0$ such that ${\mathcal R}(x) <1$. Since $\psi$ is decreasing, from (3.4),

$$\begin{aligned} G(s) \le s \psi (x) \tau ^\mathrm{A}_e, \qquad s \ge x. \end{aligned}$$

So

$$\begin{aligned} G(s) \le c_x + s \psi (x) \tau ^\mathrm{A}_e, \qquad s \ge 0, \end{aligned}$$

where $c_x = \sup _{0\le s\le x} G(x)$. By (8.2), for some $\tilde{c}_x>0$, which does not depend on the solution,

$$\begin{aligned} \sup _{-\tau _3 \le t \le T} x_3(t) \le c_3 + \tilde{c}_x + {\mathcal R}(x) \sup _{-\tau _3 \le t \le T} x_3(t). \end{aligned}$$

We reorganize,

$$\begin{aligned} \sup _{-\tau _3 \le t \le T} x_3(t) \le (1 - {\mathcal R}(x))^{-1} (c_3 + \tilde{c}_x). \end{aligned}$$

Since the right hand side does not depend on $T$, $x_3$ is bounded on $[-\tau _3, \infty )$ and

$$\begin{aligned} x_3(t) \le (1 - {\mathcal R}(x))^{-1} (c_3 + \tilde{c}_x). \end{aligned}$$

Notice from (8.3) that this is a uniform bound for a bounded set of initial data. Now $x_1$ and $x_2$ are bounded as well with the bounds being uniform for bounded sets of initial data. $\square$

Note that the method we used to prove the positiveness of solutions is also used in (Gourley et al. 2009).

Next we show that there is a bounded attractor for all solutions of the model.

Proof of Theorem 4.2

Assume that ${\mathcal R}_\infty < 1$. Let $x \ge 0$ and ${\mathcal R}(x)<1$. Then $\limsup _{t \rightarrow \infty } x_3(t) \le x$ holds for any solution of (3.3).

By Theorem 4.1, any solution is bounded. By the fluctuation method [Hirsch et al. (1985); Smith and Thieme 2011, A.3], [Thieme 2003, Prop.A.22]), for each $j \in \{1,2,3\}$, there exists a sequence $(t_k)$ with $t_k \rightarrow \infty$,

$$\begin{aligned} x_j(t_k) \rightarrow x_{j}^\infty := \limsup _{t\rightarrow \infty } x_{j}(t), \qquad x_{j}'(t_k) \rightarrow 0, \qquad k \rightarrow \infty . \end{aligned}$$

From (3.3),

$$\begin{aligned} x_1^\infty =&\frac{\gamma _3 p_3}{\eta _1} \lim _{k\rightarrow \infty } G(x_3(t_k - \tau _3)),\nonumber \\ x_{j+1}^\infty \le&\frac{\gamma _j p_j}{\eta _{j+1}} x_j^\infty , \qquad j=1,2. \end{aligned}$$

(8.4)

We substitute these inequalities into each other,

$$\begin{aligned} x_3^\infty \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \lim _{k\rightarrow \infty } G(x_3(t_k - \tau _3)). \end{aligned}$$

We can assume that $x_3^\infty > 0$. Since $x_3$ is bounded on ${ \mathbb {R}}_+$, after choosing a subsequence, $x_3(t_k - \tau _3) \rightarrow s$ for some $s \in [0, x_3^\infty ]$. Since $G$ is continuous,

$$\begin{aligned} x_3^\infty \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} G(s) . \end{aligned}$$

Since $G(0) =0$, $s \in (0, x_3^\infty ]$. By definition of $G$,

$$\begin{aligned} x_3^\infty \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \tau _e^\mathrm{A} s \psi (s) \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \tau _e^\mathrm{A} x_3^\infty \psi (s) . \end{aligned}$$

Since we have assumed that $x_3^\infty > 0$, this implies

$$\begin{aligned} 1 \le \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \tau _e^\mathrm{A} \psi (s)= {\mathcal R}(s) . \end{aligned}$$

Since $0 < s \le x_3^\infty$ and ${\mathcal R}$ is decreasing and ${\mathcal R}(x) < 1$ we have $x_3^\infty \le x$. By (8.4),

$$\begin{aligned} x_1^\infty = \frac{\gamma _3 p_3}{\eta _1} \beta \tau ^\mathrm{A}_e x , \qquad x_{2}^\infty \le \frac{\gamma _1 p_1}{\eta _{2}} x_1^\infty . \end{aligned}$$

$\square$

Appendix 2: Proofs for Sect. 5

Proof of Theorem 5.1

At first, we will consider the equilibria of system (3.3). Suppose $(x_1^*,x_2^*,x_3^*)$ is an equilibrium, then

$$\begin{aligned} \begin{aligned} 0 =&\gamma _3p_3 G(x_3^*)-\eta _1x_1^*,\\ 0 =&\gamma _1p_1 x_1^*-\eta _2 x_2^*,\\ 0 =&\gamma _2p_2 x_2^*-\eta _3 x_3^*. \end{aligned} \end{aligned}$$

It is easy to see $x_1^*=\frac{\eta _2}{\gamma _1p_1}x_2^*$, $x_2^*=\frac{\eta _3}{\gamma _2p_2}x_3^*$ and $x_3^*$ satisfies

$$\begin{aligned} x_3^*\Big (\psi (x_3^*)-\frac{\eta _1\eta _2\eta _3}{\gamma _1p_1\gamma _2p_2\gamma _3p_3\tau _e^A} \Big ) =x_3^* \Big (\psi (x_3^*)-\frac{\psi (0)}{\mathcal {R}_0}\Big )=0. \end{aligned}$$

(9.1)

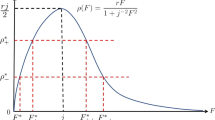
Solving (9.1), we have $x_3^*=0$ if $\mathcal {R}_0\le 1$ and $x_3^*=0$ and any $x_3^*>0$ with $\psi (x_3^*)=\frac{\psi (0)}{\mathcal {R}_0}$ if $\mathcal {R}_0> 1$ since $\psi$ is (not necessarily strictly) monotone decreasing and continuous on $[0,\infty )$. If $\psi '(x_3^*) < 0$, $x_3^*$ is uniquely determined and the nonzero equilibrium is unique.

Conversely, if ${\mathcal R}_0 >1 > {\mathcal R}_\infty$, there exists a number $x^*_3 >0$ satisfying ${\mathcal R}(x_3^*) = 1$, and defining $x_1^*$ and $x_2^*$ as above provides an equilibrium of system (3.3) in $(0,\infty )^3$.

If $\mathcal {R}_0 < 1$, then $\limsup _{t\rightarrow \infty } x_3(t) =0$ by Theorem 4.2. If ${\mathcal R}_0 =1$ and $\psi (s) < \psi (0)$, for all $s >0$, then ${\mathcal R}(s) < 1$ for all $s>0$. By Theorem 4.2, $\limsup _{t\rightarrow \infty } x_3(t)<s$ for all $s >0$ and so equals 0. It follows from the proof of Theorem 4.2 that $x_j(t) \rightarrow 0$ as $t \rightarrow \infty$ for $j=1,2$.

Local asymptotic stability of the trivial equilibrium if ${\mathcal R}_0< 1$ follows from a standard analysis of a characteristic equation which is similar to the one we will do for the positive equilibrium and is therefore omitted.

Let $\mathcal {R}_0>1$. To study the local asymptotic stability of the positive equilibrium, we use the principle of linearized stability [see Hale and Verdyun Lunel (1993), e.g.]. The linearization of system (3.3) at the positive equilibrium leads to the characteristic equation

$$\begin{aligned} (\lambda +\eta _1)(\lambda +\eta _2)(\lambda +\eta _3) = (\psi (x_3^*)+\psi '(x_3^*)x_3^*)\tau _e^A\gamma _1p_1\gamma _2p_2\gamma _3p_3 e^{-\lambda (\tau _1+\tau _2+\tau _3)}. \end{aligned}$$

(9.2)

By (4.1) and ${\mathcal R}(x_3^*)=1$,

$$\begin{aligned} (\lambda +\eta _1)(\lambda +\eta _2)(\lambda +\eta _3) = \Big (1 +\frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} \Big ) \eta _1 \eta _2 \eta _2 e^{-\lambda (\tau _1+\tau _2+\tau _3)}. \end{aligned}$$

(9.3)

Since $\psi '(x_3^*) < 0$, there is no nonnegative root.

Suppose that there is a root $\lambda$ with $\mathfrak {R}\lambda \ge 0$ and $\mathfrak {I}\lambda \ne 0$. Then, by taking absolute values,

$$\begin{aligned} \eta _1 \eta _2\eta _3 < \Big |1 +\frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} \Big | \eta _1 \eta _2 \eta _2. \end{aligned}$$

(9.4)

This implies

$$\begin{aligned} \frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} < -2. \end{aligned}$$

(9.5)

By contraposition, the interior equilibrium is locally asymptotically stable if

$$\begin{aligned} \frac{\psi '(x_3^*)x_3^* }{\psi (x_3^*)} \ge -2. \end{aligned}$$

(9.6)

$\square$

1.1 Persistence

Proof of Theorem 5.2

If ${\mathcal R}_0 > 1$, the questing adult ticks are uniformly weakly persistent: There exists some $\epsilon >0$ such that $x_3^{\infty }\geqslant \epsilon$ for any solution whose initial data satisfy (3.8).

Let $\epsilon >0$. Assume that there exists a solution $(x_1(t),x_2(t),x_3(t))$ satisfying (3.8) and

$$\begin{aligned} x_3^{\infty }=\lim _{t\rightarrow \infty } \sup x_3(t)< \epsilon . \end{aligned}$$

(9.7)

Then we have $x_3(t-\tau _3)< \epsilon$ for sufficiently large $t$. Since $\psi (x_3)$ is a decreasing function, we have $\psi (x_3(t-\tau _3))\geqslant \psi (\epsilon )$. After a shift forward in time, we have the following inequality

$$\begin{aligned} \begin{aligned} \dfrac{\mathrm {d}x_1(t)}{\mathrm {d}t}&\geqslant \displaystyle x_3(t - \tau _3)\gamma _3p_3\tau _e^A \psi (\epsilon )-\eta _1x_1(t), \qquad t \ge 0. \end{aligned} \end{aligned}$$

Using the method in (Smith and Thieme 2011), we take the Laplace transform in both sides of the above inequality with $\lambda > 0$,

$$\begin{aligned} \lambda \fancyscript{L}(x_1(t))&\geqslant -\eta _1\fancyscript{L}(x_1(t))+\gamma _3p_3\tau _e^A \psi (\epsilon ) \int _0^{\infty }e^{-\lambda s}x_3(s-\tau _3)\mathrm {d}s\\&= -\eta _1\fancyscript{L}(x_1(t))+\gamma _3p_3\tau _e^A \psi (\epsilon )e^{-\lambda \tau _3}\int _{-\tau _3}^{\infty } e^{-\lambda s}x_3(s)\mathrm {d}s\\&\geqslant -\eta _1\fancyscript{L}(x_1(t))+\gamma _3p_3\tau _e^A \psi (\epsilon )e^{-\lambda \tau _3} \int _{0}^{\infty }e^{-\lambda s}x_3(s)\mathrm {d}s. \end{aligned}$$

We drop the term $\int _{-\tau }^0e^{-\lambda s}x_3(s)\mathrm {d}s$ because $x_3(s)$ is nonnegative. Rearranging gives

$$\begin{aligned} \fancyscript{L}(x_1(t))\ge \frac{\gamma _3p_3\tau _e^A \psi (\epsilon )e^{-\lambda \tau _3}}{\lambda +\eta _1}\fancyscript{L}(x_3(t)). \end{aligned}$$

(9.8)

Similarly, we take Laplace transform on both sides of equations for $x_2(t)$ and $x_3(t)$ in (3.3). Simplification gives

$$\begin{aligned} \fancyscript{L}(x_2(t))\ge \frac{\gamma _1p_1e^{-\lambda \tau _1}}{\lambda +\eta _2} \fancyscript{L}(x_1(t)) \end{aligned}$$

(9.9)

and

$$\begin{aligned} \fancyscript{L}(x_3(t))\ge \frac{\gamma _2p_2e^{-\lambda \tau _2}}{\lambda +\eta _3} \fancyscript{L}(x_2(t)). \end{aligned}$$

(9.10)

We combine (9.8), (9.9) and (9.10),

$$\begin{aligned} \begin{aligned} \fancyscript{L}(x_1(t))\ge \frac{\tau _e^A\psi (\epsilon ) \gamma _1p_1\gamma _2 p_2\gamma _3 p_3 e^{-\lambda (\tau _1+\tau _2+\tau _3)}}{(\lambda +\eta _1)(\lambda +\eta _2)(\lambda +\eta _3)} \fancyscript{L}(x_1(t)). \end{aligned} \end{aligned}$$

Noting that $\fancyscript{L}(x_1(t))>0$ because $x_1(t)$ is eventually positive, we divide by $\fancyscript{L}(x_1(t))$ on both sides and obtain

$$\begin{aligned} \begin{aligned} 1\ge \frac{\tau _e^A\psi (\epsilon )\gamma _1p_1\gamma _2 p_2\gamma _3 p_3 e^{-\lambda (\tau _1+\tau _2+\tau _3)}}{(\lambda +\eta _1)(\lambda +\eta _2) (\lambda +\eta _3)}. \end{aligned} \end{aligned}$$

If the questing adults ticks are not uniformly weakly persistent as formulated in the theorem, the last inequality holds for all $\lambda >0$ and $\epsilon >0$. Letting $\lambda \rightarrow 0$ and $\epsilon \rightarrow 0$, we obtain

$$\begin{aligned} \begin{aligned} 1\ge \frac{\tau _e^A\psi (0)\gamma _1p_1\gamma _2 p_2\gamma _3 p_3 }{\eta _1\eta _2\eta _3} = {\mathcal R}_0. \end{aligned} \end{aligned}$$

Recall (4.1) and (4.2). By contraposition, the questing adult ticks are uniformly weakly persistent if $\mathcal {R}_0>1$. $\square$

Proof of Theorem 5.3

Consider system (3.3). If $\mathcal {R}_0 >1> {\mathcal R}_\infty$, the tick population is uniformly persistent: There exists some $\epsilon >0$ such that $x_{1\infty }\geqslant \epsilon$, $x_{2\infty }\geqslant \epsilon$ and $x_{3\infty }\geqslant \epsilon$ for any solution whose initial data satisfy (3.8).

We will use Theorem 4.12 in (Smith and Thieme 2011) to prove the uniform persistence for questing adult ticks.

Choose the state space $X$ as the cone of nonnegative functions in $C [-\tau _1,0] \times C[-\tau _2,0] \times C[-\tau _3,0]$.

Assume that $x(t)=(x_1(t),\ x_2(t),\ x_3(t))$ is a solution of (3.3) with nonnegative initial data $\phi \in X$. Define a subset

$$\begin{aligned} D=\{x_t(\phi )\in X: 0\leqslant x_t^i (\phi )\leqslant M_i,\ i=1,2,3, \ t\geqslant \tau \}, \end{aligned}$$

where $\tau = \max _{i=1}^3 \tau _i$, $x_t^i(\phi )$ is the $i$-th component of $x_t$ and the $M_i$ have been chosen that $\limsup _{t \rightarrow \infty } x_i(t) < M_i$ (see Theorem 4.2).

It is easy to verify that $D$ is a bounded subset of $X$ and, by construction, attracts all $x\in X$. It follows that $|x'(t)|$ is uniformly bounded by a constant $\bar{M}=\bar{M}(M_1,M_2,M_3)$ on $\{t\geqslant \tau \}$ independent of the solution in $D$. From the Ascoli-Arzela Theorem [Ch.8.3 in McDonald and Weiss (1999)], the subset $D$ has compact closure because $\{x_t(\phi )\in D, t\geqslant \tau \}$ is an equicontinuous and equibounded subset of $C [-\tau _1,0] \times C[-\tau _2,0] \times C[-\tau _3,0]$.

So we have found a compact set that attracts all points in $X$.

We define $\rho :X\rightarrow \mathbb {R}_+$ by

$$\begin{aligned} \rho (x_0)= x_{30}(0),\qquad x_0=(x_{10},x_{20},x_{30})\in X. \end{aligned}$$

Then $\rho$ is continuous and $\rho (x_t(\phi ))=x_3(t)$.

We check the three assumptions $\hat{\heartsuit }_1-\hat{\heartsuit }_3$ in [Smith and Thieme (2011) Thm.4.13]. Assumption $\hat{\heartsuit }_1$ and $\hat{\heartsuit }_2$ are true because the set $D$ attracts all $x\in X$ and the closure of $D$ is compact. By (3.3), $\rho (x_0)>0$ implies $\rho (x_t(\phi ))>0$ for all $t\geqslant \tau$. This verifies $\hat{\heartsuit }_3$. By Theorem 5.2, system (3.3) is uniformly weakly $\rho$-persistent.

By Theorem 4.12 in (Smith and Thieme 2011), the system (3.3) is uniformly $\rho$-persistent whenever it is uniformly weakly $\rho$-persistent. So there exists some $\epsilon _3 >0$ such that

$$\begin{aligned} \liminf _{t\rightarrow \infty } x_3(t) \ge \epsilon _3 \end{aligned}$$

for all solutions of (3.3) whose initial data satisfy (3.8).

We apply the fluctuation method to the differential equation for $x_1$,

$$\begin{aligned} x_1'(t) = \gamma _3 p_3 G (x_3(t-\tau _3)) - \eta _1 x_1(t). \end{aligned}$$

There exists a sequence $(t_k)$ with $t_k \rightarrow \infty$, $x_1(t_k) \rightarrow x_{1\infty }$, $x_1'(t_k ) \rightarrow 0$ as $k \rightarrow \infty$. So

$$\begin{aligned} x_{1\infty } = \lim _{k\rightarrow \infty } \frac{\gamma _3 p_3}{\eta _1} G (x_3(t_k-\tau _3)) \ge \frac{\gamma _3 p_3}{\eta _1} \min \{G(x_3); \epsilon _3 \le x_3 \le M_3\} =: \epsilon _1 > 0. \end{aligned}$$

Similarly, one finds some $\epsilon _2 >0$ that does not depend on the initial conditions such that $x_{2\infty } \ge \epsilon _2$.

By Theorem 4.1, any solution whose initial data satisfies (3.8) fulfills $\rho (x_3(r)) >0$ for some $r >0$ and so $x_{j\infty } \ge \epsilon _j$ for $j =1,2,3$. $\square$

1.2 Global stability of the positive equilibrium

To prove the global stability result for the interior equilibrium, we will rewrite (3.3) as a scalar integral equation for $x_3$ and use Theorem B.40 in (Thieme 2003).

All equations of the system (3.3) are of the form

$$\begin{aligned} u'(t) = \alpha v(t-\tau ) - \mu u(t), \qquad t \ge 0. \end{aligned}$$

(9.11)

By the variation of constants formula,

$$\begin{aligned} u(t)&= \int _0^t \alpha v(s-\tau ) e^{-\mu (t-s)} ds + u(0) e^{-\mu t} = \int _{-\tau }^{t-\tau } \alpha v(s) e^{-\mu (t-s - \tau )} ds\\&+ u(0) e^{-\mu t}. \end{aligned}$$

Then $u$ can be written as

$$\begin{aligned} u(t) = \int _0^t v(s) k(t-s) ds + u_0 (t), \end{aligned}$$

(9.12)

where

$$\begin{aligned} k(t) = \left\{ \begin{array}{cc} \alpha e^{-\mu (t-\tau )} ; &{}\quad t \ge \tau \\ 0 ; &{} t \le \tau \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} u_0(t ) = \int _{-\tau }^0 \alpha v(s) k(t-s) ds + u(0) e^{-\mu t}. \end{aligned}$$

Notice that $u_0(t) \rightarrow 0$ as $t \rightarrow \infty$ and

$$\begin{aligned} \int _0^\infty k(t) dt = \frac{\alpha }{\mu }. \end{aligned}$$

(9.13)

Now let $v$ also be given in the form

$$\begin{aligned} v(s) = \int _0^s w(r) \ell (s-r) dr + v_0(s), \qquad s \ge 0, \end{aligned}$$

with $v_0(s) \rightarrow 0$ as $s \rightarrow \infty$. Then

$$\begin{aligned} u(t) = \int _0^t \Big ( \int _0^s w(r) \ell (s-r) dr + v_0(s) \Big ) k(t-s) ds + u_0(t). \end{aligned}$$

We change the order of integration

$$\begin{aligned} u(t) = \int _0^t w(r) \Big (\int _r^t \ell (s-r) k(t-s) ds \Big ) dr + \int _0^t v_0(s) k(t-s) ds + u_0(t). \end{aligned}$$

After a substitution,

$$\begin{aligned} u(t) = \int _0^t w(r) \Big (\int _0^{t-r} \ell (s) k(t-r-s) ds \Big ) dr + \tilde{u}_0(t) \end{aligned}$$

with

$$\begin{aligned} \tilde{u}_0(t) = \int _0^t v_0(s) k(t-s) ds + u_0(t). \end{aligned}$$

Finally,

$$\begin{aligned} u(t) = \int _0^t w(r) m (t-r) dr + \tilde{u}_0(t) \end{aligned}$$

(9.14)

with

$$\begin{aligned} m (t) = \int _0^t \ell (s) k(t-s) ds \end{aligned}$$

and

$$\begin{aligned} \tilde{u}_0(t) \rightarrow 0, \quad t \rightarrow \infty . \end{aligned}$$

Notice that

$$\begin{aligned} \int _0^\infty m(t) dt = \Big ( \int _0^\infty \ell (t) dt \Big ) \Big ( \int _0^\infty k(t) dt \Big ). \end{aligned}$$

(9.15)

We apply this procedure to (3.3),

$$\begin{aligned} x_1(t) =&\int _0^t G(x_3(s)) K_1(t-s)ds + \tilde{x}_1(t),\nonumber \\ x_2(t) =&\int _0^t x_1(s) K_2(t-s) ds + \tilde{x}_2(t),\nonumber \\ x_3(t) =&\int _0^t x_2(s) K_3(t-s) ds + \tilde{x}_3 (t), \end{aligned}$$

(9.16)

with $\tilde{x}_j(t) \rightarrow 0$ and

$$\begin{aligned} \int _0^\infty K_1(t)dt = \frac{\gamma _3 p_3}{\eta _1}, \qquad \int _0^\infty K_2(t)dt = \frac{\gamma _1 p_1}{\eta _2}, \qquad \int _0^\infty K_3(t) dt = \frac{\gamma _2 p_2}{\eta _3}. \end{aligned}$$

We substitute these integral equations into each other; by the procedure above we obtain the integral equation

$$\begin{aligned} x_3(t) = \int _0^t G(x_3(s)) K(t-s) ds + \bar{x}_3(t), \end{aligned}$$

(9.17)

with $\bar{x}_3(t) \rightarrow 0$ as $t \rightarrow \infty$ and

$$\begin{aligned} \int _0^\infty K(t) dt = \prod _{j=1}^3 \int _0^\infty K_j(t) dt = \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j}. \end{aligned}$$

(9.18)

All solution of (3.3) satisfying (3.8) are solutions of (9.17) that are bounded and bounded away from zero. The latter follows from Theorem 5.3.

To bring this equation into the form of Theorem B.40 in (Thieme 2003), we normalize $K$ and set

$$\begin{aligned} f(x_3) = \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} G(x_3) = \prod _{j=1}^3 \frac{\gamma _j p_j}{\eta _j} \tau _e^\mathrm{A} x_3 \psi (x_3) . \end{aligned}$$

(9.19)

By (4.1),

$$\begin{aligned} f(x_3) = x_3 {\mathcal R}( x_3 ). \end{aligned}$$

(9.20)

We see that a fixed point of $f$, $f(x_3) = x_3$, corresponds to the third coordinate of an interior equilibrium for which ${\mathcal R}(x_3)=1$. Since ${\mathcal R}_0 > 1$, $f(x_3) > x_3$ if $x_3 > 0$ is small and $f(x_3) < x_3$ if $x_3 >0$ is large. By Theorem B.40 in (Thieme 2003), all solutions of (9.17) that are bounded and bounded away from zero converge to $x_3^*$ if $x^*_3$ is the only $z > 0$ with $f(f(z)) = z$.

The latter condition is satisfied if all solutions of the difference equation $z_{n+1} = f(z_n)$ converge to $x_3^*$ if the initial datum satisfies $z_0 >0$.

Proof of Corollaries 5.5 and 5.4

If $s^2 \psi (s)$ is a strictly increasing function of $s$, i.e., $s f(s)$ is a strictly increasing function of $s \ge 0$, this follows from [Thieme (2003), Cor.9.9].

If $\psi (s) = \beta e^{-\alpha s}$, we rescale $z_n = x^* y_n$. Notice that ${\mathcal R}_0 = e^{\alpha x_3^*}$. Then

$$\begin{aligned} y_{n+1} = y_n e^{x^*(1-y_n)}. \end{aligned}$$

By [Thieme (2003), Thm.9.16], all solutions $(y_n)$ of this difference equation converge to 1 for $y_0 > 0$ if and only if $2 \ge \alpha x_3^* = \ln {\mathcal R}_0$. This proves that the interior equilibrium attracts all solutions with nontrivial initial conditions.

For the local stability, Notice that $\psi '(x_3^*)=-\alpha \beta e^{-\alpha x^*}=-\alpha \psi (x_3^*)<0$. The stability condition in Theorem 5.1 becomes $\alpha x_3^* \le 2$. Since $\psi (x_3^*)= \frac{\psi (0)}{{\mathcal R}_0}$, $e^{-\alpha x_3^*} = 1/{\mathcal R}_0$ and $\alpha x_3^* = \ln {\mathcal R}_0$. This implies the assertion. $\square$