Method of conditional moments (MCM) for the Chemical Master Equation

Abstract

The time-evolution of continuous-time discrete-state biochemical processes is governed by the Chemical Master Equation (CME), which describes the probability of the molecular counts of each chemical species. As the corresponding number of discrete states is, for most processes, large, a direct numerical simulation of the CME is in general infeasible. In this paper we introduce the method of conditional moments (MCM), a novel approximation method for the solution of the CME. The MCM employs a discrete stochastic description for low-copy number species and a moment-based description for medium/high-copy number species. The moments of the medium/high-copy number species are conditioned on the state of the low abundance species, which allows us to capture complex correlation structures arising, e.g., for multi-attractor and oscillatory systems. We prove that the MCM provides a generalization of previous approximations of the CME based on hybrid modeling and moment-based methods. Furthermore, it improves upon these existing methods, as we illustrate using a model for the dynamics of stochastic single-gene expression. This application example shows that due to the more general structure, the MCM allows for the approximation of multi-modal distributions.

Appendices

Appendix A: Proof of Lemma 1

The differentiation of $\mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)$ results in

$$\begin{aligned} \frac{\partial }{\partial t} \left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) = \sum _{z\ge 0}T(z,t) \frac{\partial }{\partial t} p(y,z|t) + \sum _{z\ge 0} p(y,z|t) \frac{\partial }{\partial t} T(z,t), \end{aligned}$$

which we reformulate as

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \nonumber \\&\quad \!=\!\sum _{z\ge 0}T(z,t) \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+}\\ z \!\ge \! \nu _{j,z}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) h_{j}(z\!-\!\nu _{j,z}) p(z\!-\!\nu _{j,z}|y-\nu _{j,y},t) p(y-\nu _{j,y}|t)\nonumber \\&\quad - \sum _{z\ge 0}T(z,t) \sum _{j=1}^{n_{r}} c_j g_{j}(y) h_{j}(z) p(z|y,t) p(y|t)+ p(y|t) \sum _{z\ge 0} p(z|y,t) \frac{\partial }{\partial t} T(z,t) \end{aligned}$$

by substitution of $\frac{\partial }{\partial t} p(y,z|t)$ with (9) and the use of the multiplication axiom (3). Next we change the order of summation and substituting in the first sum $z \rightarrow z + \nu _{j,z}$, yielding

$$\begin{aligned}&\frac{\partial }{\partial t} \left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \sum _{z \ge \nu _{j,z}^-} T(z+\nu _{j,z},t) h_{j}(z) p(z|y-\nu _{j,y},t) p(y-\nu _{j,y}|t) \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \sum _{z \ge 0} T(z,t) h_{j}(z) p(z|y,t) p(y|t) + p(y|t) \sum _{z\ge 0} p(z|y,t) \frac{\partial }{\partial t} T(z,t) \end{aligned}$$

This equation can be reformulated further by exploiting the fact that the CME is proper, meaning that $h_{j}(z) = 0$ whenever $z \ngeq \nu _{j,z}^-$. Accordingly, the limit of the first summation over $z, z \ge \nu _{j,z}^-$, can be set to zero, $z \ge 0$. Using the definition of the conditional expectation (8) we obtain (10) which concludes the proof. $\square$

Note that the manipulations of infinite sums are allowed under absolute convergence, which holds for any test-function $T(z,t)$ which is polynomial in $z$ if for all $t$ sufficiently many moments of $p(y,z|t)$ with respect to $z$ exist (Engblom 2006). Note that Lemma 1 is a generalization of a result by Engblom (2006, Lemma 2.1).

Appendix B: Proof of Proposition 2

We consider the conditional mean weighted by the corresponding probability, $\mu _{i,z}(y,t) p(y|t) = \sum _{z \ge 0} z_i p(y,z|t)$. By differentiating this product with respect to $t$ we readily obtain

$$\begin{aligned} p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t) = \frac{\partial }{\partial t} \left( \mu _{i,z}(y,t) p(y|t)\right) - \mu _{i,z}(y,t) \frac{\partial }{\partial t} p(y|t). \end{aligned}$$

(39)

The unknown derivative $\frac{\partial }{\partial t} \left( \mu _{i,z}(y,t) p(y|t)\right)$ follows from Lemma 1 by choosing the test function $T(Z,t) = Z_i$,

$$\begin{aligned}&\frac{\partial }{\partial t}\left( \mu _{i,z}(y,t) p(y|t)\right) \nonumber \\&\quad = \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \mathbb E _{z}\left. \left[ (Z_i+\nu _{ij,z}) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ Z_i h_{j}(Z)\right| y,t\right] p(y|t). \end{aligned}$$

(40)

This derivative depends on $\mathbb E _{z}\left. \left[ (Z_i+\nu _{ij,z}) h_{j}(Z)\right| y-\nu _{j,y},t\right]$ and $\mathbb E _{z}\left. \left[ Z_i h_{j}(Z)\right| y,t\right]$. By adding and subtracting the conditional means we can reformulate these conditional expectations to

$$\begin{aligned} \mathbb E _{z}\left. \left[ Z_i h_{j}(Z)\right| y,t\right]&= \mathbb E _{z}\left. \left[ (Z_i - \mu _{i,z}(y,t) + \mu _{i,z}(y,t)) h_{j}(Z)\right| y,t\right] \nonumber \\&= \mathbb E _{z}\left. \left[ (Z - \mu _{z}(y,t))^{e_i} h_{j}(Z)\right| y,t\right] \nonumber \\&+ \mu _{i,z}(y,t) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y,t\right] \end{aligned}$$

(41)

and

$$\begin{aligned}&\mathbb E _{z}\left. \left[ (Z_i+\nu _{ij,z}) h_{j}(Z)\right| y-\nu _{j,y},t\right] \nonumber \\&\quad = \mathbb E _{z}\left. \left[ (Z_i- \mu _{i,z}(y-\nu _{j,y},t) + \mu _{i,z}(y-\nu _{j,y},t)+\nu _{ij,z}) h_{j}(Z)\right| y - \nu _{j,y},t\right] \nonumber \\&\quad = \mathbb E _{z}\left. \left[ (Z - \mu _{z}(y-\nu _{j,y},t))^{e_i} h_{j}(Z)\right| y - \nu _{j,y},t\right] \nonumber \\&\qquad + (\mu _{i,z}(y-\nu _{j,y},t)+\nu _{ij,z}) \mathbb E _{z}\left. \left[ h_{j}(Z)\right| y - \nu _{j,y},t\right] . \end{aligned}$$

(42)

Substitution of these reformulated conditional expectations into (40) followed by the insertion of (40) into (39) yields the evolution equation for the conditional mean (16), which concludes the proof of Proposition 2. $\square$

Appendix C: Proof of Proposition 3

We consider the product $C_{I,z}(y,t) p(y|t)$ and differentiate it with respect to time, which readily yields

$$\begin{aligned} p(y|t) \frac{\partial }{\partial t} C_{I,z}(y,t) = \frac{\partial }{\partial t} \left( C_{I,z}(y,t) p(y|t)\right) - C_{I,z}(y,t) \frac{\partial }{\partial t} p(y|t). \end{aligned}$$

(43)

Using Lemma 1 with $T(Z,t) = (Z-\mu _{z}(y,t))^I$, we obtain

$$\begin{aligned}&\frac{\partial }{\partial t}\left( C_{I,z}(y,t) p(y|t)\right) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \mathbb E _{z}\left. \left[ (Z\!+\!\nu _{j,z}-\mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^I h_{j}(Z)\right| y,t\right] p(y|t)\nonumber \\&\qquad - \sum _{\begin{array}{c} i=1\\ I_i \ge 1 \end{array}}^{n_{s,z}} I_i \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^{I-e_i}\right| y,t\right] p(y|t) \frac{\partial }{\partial t} \mu _{i,z}(y,t), \end{aligned}$$

(44)

where the third sum corresponds to the term $\mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,t)\right| y,t\right] p(y|t)$ in (10) and

$$\begin{aligned} \forall i \in \{1,\ldots ,{n_{s,z}}\} \hbox { with } I_i \ge 1: \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,t))^{I-e_i}\right| y,t\right] = C_{I-e_i,z}(y,t).\qquad \end{aligned}$$

(45)

After substituting (43) and (45) into (44), it remains for us to prove that (23) holds. Therefore, we add and subtract $\mu _{z}(y-\nu _{j,y},t)$ in $(Z+\nu _{j,z}-\mu _{z}(y-\nu _{j,y},t))^I$ and apply the multinomial theorem, yielding

$$\begin{aligned}&(Z+\nu _{j,z}-\mu _{z}(y,t))^I \nonumber \\&\quad = (Z-\mu _{z}(y-\nu _{j,y},t)+\mu _{z}(y-\nu _{j,y},t)-\mu _{z}(y,t)+\nu _{j,z})^I\nonumber \\&\quad = \sum _{0 \le k \le I} \begin{pmatrix} I \\ k \end{pmatrix} \left( \mu _{z}(y-\nu _{j,y},t)-\mu _{z}(y,t)+\nu _{j,z}\right) ^{I-k} (Z-\mu _{z}(y-\nu _{j,y},t))^{k}, \nonumber \\ \end{aligned}$$

(46)

where the summation runs over all vectors $k \in \mathbb N _0^{n_{s,z}}$ for which $k_i \in [0,I_i]$ for all $i$. By substituting (46) into $\mathbb E _{z}\left. \left[ (Z+\nu _{j,z}-\mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right]$ and employing that the expectation of a sum is the sum of the expectations, we arrive at (23), which concludes the proof. $\square$

Appendix D: Proof of Proposition 4

For $i \in \{1,{n_{s,y}}\}$ Eq. (29) states merely the definition of the mean. The result for ${n_{s,y}} < i \le {n_{s}}$ follows from

$$\begin{aligned} \bar{\mu }_i(t) = \sum _{y\ge 0} \sum _{z\ge 0} z_{j} p(y,z|t) = \sum _{y\ge 0} \underbrace{\sum _{z\ge 0} z_{j} p(z|y,t)}_{\displaystyle = \mu _{j,z}(y,t)} p(y|t), \hbox { with } j = i-{n_{s,y}}, \end{aligned}$$

which concludes the proof of (29). The result for the centered moment ${\bar{C}}_{I}(t)$ is obtained by a reordering of the sums and the application of the multiplication axiom (3):

$$\begin{aligned} {\bar{C}}_{I}(t)&= \sum _{y\ge 0} \sum _{z\ge 0} (y - \bar{\mu }_{y}(t))^{I_y} (z - \bar{\mu }_{z}(t))^{I_z} p(y,z|t) \\&= \sum _{y\ge 0} (y - \bar{\mu }_{y}(t))^{I_y} \sum _{z\ge 0} (z - \bar{\mu }_{z}(t))^{I_z} p(z|y,t)p(y|t). \end{aligned}$$

In order to arrive at the term $(z - \mu _{z}(y,t))^{I_z}$, we add and subtract $\mu _{z}(y,t)$. This yields $(z - \mu _{z}(y,t) + \mu _{z}(y,t) - \bar{\mu }_{z}(t))^{I_z}$ and reformulation in terms of $(\mu _{z}(y,t)- \bar{\mu }_z(t))$ and $(z - \mu _{z}(y,t))$ using the multinomial theorem gives

$$\begin{aligned} {\bar{C}}_{I}(t)&= \sum _{y \ge 0}{(y - {\bar{\mu }}_{y}(t))}^{I_y} \sum _{z \ge 0} \sum _{0 \le k \le I_z} \begin{pmatrix} I_z \\ k \end{pmatrix} (\mu _{z}(y,t)\nonumber \\&- {{\bar{\mu }}_z(t))}^{I_z-k} \cdot (z - \mu _{z}(y,t))^{k} p(z|y,t)p(y|t). \end{aligned}$$

Finally, we exchange the two inner sums and substitute $\sum _{z\ge 0} (z - \mu _{z}(y,t))^{k} p(z|y,t)$ by $C_{k,z}(y,t)$. The modified equation for ${\bar{C}}_{I}(t)$ becomes (30) which concludes the proof. $\square$

Appendix E: Initial conditions for states $y$ with $p(y|0) = 0$

Proposition 5

Given an initial distribution $p(y,z|0)$, a state $y$ with $p(y|0) = 0$, and the differentiation index $K_y$ with $\forall k \in \{1,\ldots ,K_y-1\}: \partial _{t}^{k}p(y|0) = 0$ and $\partial _{t}^{K_y}p(y|0) \ne 0$, the initial conditional moments for (24) are

$$\begin{aligned}&\partial _{t}^{K_y}p(y|0) \mu _{i,z}(y,0) \nonumber \\&\quad = \sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \left. \frac{\partial ^{K_y-1}}{\partial t^{K_y-1}}\left( \mathbb E _{z}\left. \left[ (Z+\nu _{j,z})^{e_i} h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0} \nonumber \\ \end{aligned}$$

(47)

and

$$\begin{aligned}&\partial _{t}^{K_y}p(y|0) C_{I,z}(y,0) \nonumber \\&\quad \!=\!\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^+ \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \left. \frac{\partial ^{K_y-1}}{\partial t^{K_y-1}}\left( \mathbb E _{z}\left. \left[ (Z + \nu _{j,z}\!-\! \mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y\!-\!\nu _{j,y}|t)\right) \right| _{t=0},\nonumber \\ \end{aligned}$$

(48)

$$\begin{aligned}&(K_y+1) \partial _{t}^{K_y}p(y|0) \dot{\mu }_{i,z}(y,0) + \partial _{t}^{K_y+1}p(y|0) \mu _{i,z}(y,0) \nonumber \\&\quad ={\mathop {\mathop {\mathop {\sum }\limits _{j=1}}\limits _{y \ge \nu _{j,y}^{+}}}\limits ^{n_{r}}} c_j g_{j}(y-\nu _{j,y}) \left. \frac{\partial ^{K_y}}{\partial t^{K_y}} \left( \mathbb E _{z}\left. \left[ (Z+\nu _{j,z})^{e_i} h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0}\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ Z^{e_i} h_{j}(Z)\right| y,0\right] \partial _{t}^{K_y}p(y|0), \end{aligned}$$

(49)

and

$$\begin{aligned}&(K_y+1) \partial _{t}^{K_y}p(y|0) \dot{C}_{I,z}(y,0) + \partial _{t}^{K_y+1}p(y|0) C_{I,z}(y,0)\nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \left. \frac{\partial ^{K_y}}{\partial t^{K_y}} \left( \mathbb E _{z}\left. \left[ (Z \!+\! \nu _{j,z}- \mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0}\nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ (Z-\mu _{z}(y,0))^{I} h_{j}(Z)\right| y,0\right] \partial _{t}^{K_y}p(y|0)\nonumber \\&\qquad - \sum _{\begin{array}{c} i=1\\ I_i \ge 1 \end{array}}^{n_{s,z}} I_i C_{I-e_i,z}(y,0) \dot{\mu }_{i,z}(y,0) \partial _{t}^{K_y}p(y|0). \end{aligned}$$

(50)

Proof

To prove Proposition 5, we consider a general test function $T(Z,t)$ and its conditional expectation $\mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right]$. It can be shown using Leibniz rule that for any $L \in \mathbb N$,

$$\begin{aligned} \frac{\partial ^{L}}{\partial t^{L}}\left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) = \sum _{k=0}^L \begin{pmatrix} L \\ k \end{pmatrix} \left( \frac{\partial ^{k}}{\partial t^{k}} p(y|t)\right) \left( \frac{\partial ^{L-k}}{\partial t^{L-k}}\mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] \right) . \nonumber \\ \end{aligned}$$

(51)

Furthermore, by applying the differentiation operator $\frac{\partial ^{L-1}}{\partial t^{L-1}}$ to (10) it follows from Lemma 1 that

$$\begin{aligned}&\frac{\partial ^L}{\partial t^L}\left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \frac{\partial ^{L-1}}{\partial t^{L-1}} \left( \mathbb E _{z}\left. \left[ T(Z+\nu _{j,z},t) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \frac{\partial ^{L-1}}{\partial t^{L-1}}\left( \mathbb E _{z}\left. \left[ T(Z,t) h_{j}(Z)\right| y,t\right] p(y|t)\right) \nonumber \\&\qquad + \frac{\partial ^{L-1}}{\partial t^{L-1}}\left( \mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,t)\right| y,t\right] p(y|t)\right) . \end{aligned}$$

Using the general Leibniz rule this equation can be reformulated to

$$\begin{aligned}&\frac{\partial ^L}{\partial t^L}\left( \mathbb E _{z}\left. \left[ T(Z,t)\right| y,t\right] p(y|t)\right) \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y\!-\!\nu _{j,y}) \frac{\partial ^{L-1}}{\partial t^{L-1}} \left( \mathbb E _{z}\left. \left[ T(Z\!+\!\nu _{j,z},t) h_{j}(Z)\right| y\!-\!\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \sum _{k=0}^{L-1} \begin{pmatrix} L-1 \\ k \end{pmatrix} \left( \frac{\partial ^{L-k-1}}{\partial t^{L-k-1}} \mathbb E _{z}\left. \left[ T(Z,t) h_{j}(Z)\right| y,t\right] \right) \left( \frac{\partial ^{k}}{\partial t^{k}} p(y|t)\right) \nonumber \\&\qquad + \sum _{k=0}^{L-1} \begin{pmatrix} L-1 \\ k \end{pmatrix} \left( \frac{\partial ^{L-k-1}}{\partial t^{L-k-1}} \mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,t)\right| y,t\right] \right) \left( \frac{\partial ^{k}}{\partial t^{k}} p(y|t)\right) . \end{aligned}$$

(52)

By evaluating (51) and (52) at $t = 0$ for $L = K_y$ and employing that $\forall k \in \{1,\ldots ,K_y-1\}: \partial _{t}^{k}p(y|0) = 0$ we obtain

$$\begin{aligned}&\partial _{t}^{K_y}p(y|0) \mathbb E _{z}\left. \left[ T(Z,0)\right| y,0\right] \nonumber \\&\quad =\sum _{\begin{array}{c} j=1 \\ y \ge \nu _{j,y}^{+} \end{array}}^{n_{r}} c_j g_{j}(y-\nu _{j,y}) \left. \frac{\partial ^{K_y-1}}{\partial t^{K_y-1}} \left( \mathbb E _{z}\left. \left[ T(Z+\nu _{j,z},t) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0}. \nonumber \\ \end{aligned}$$

(53)

As $\partial _{t}^{K_y}p(y|t)$ is non-zero, (53) defines the initial values $\mathbb E _{z}\left. \left[ T(Z,0)\right| y,0\right]$. The Eqs. (47) and (48) for the initial conditions $\mu _{i,z}(y,0)$ and $C_{I,z}(y,0)$ follow for $T(Z,t) = Z_i$ and $T(Z,t) = (Z - \mu _{z}(y,t))^I$, respectively.

To derive equations for the initial derivatives $\dot{\mu }_{i,z}(y,0)$ and $\dot{C}_{I,z}(y,0)$ we evaluate (51) and (52) at $t = 0$ for $L = K_y+1$. Employing $\forall k \in \{1,\ldots ,K_y-1\}: \partial _{t}^{k}p(y|0) = 0$, this yields

$$\begin{aligned}&(K_y+1) \partial _{t}^{K_y}p(y|0) \dot{\mathbb{E }}_{z}\left. \left[ T(Z,0)\right| y,0\right] + \partial _{t}^{K_y+1}p(y|0) \mathbb E _{z}\left. \left[ T(Z,0)\right| y,0\right] \nonumber \\&\quad ={\mathop {\mathop {\sum }\limits _{j=1}}\limits _{y \ge \nu _{j,y}^{+}}^{n_{r}}} c_j g_{j}(y-\nu _{j,y}) \left. \frac{\partial ^{K_y}}{\partial t^{K_y}} \left( \mathbb E _{z}\left. \left[ T(Z+\nu _{j,z},t) h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)\right) \right| _{t=0} \nonumber \\&\qquad - \sum _{j=1}^{n_{r}} c_j g_{j}(y) \mathbb E _{z}\left. \left[ T(Z,0) h_{j}(Z)\right| y,0\right] \partial _{t}^{K_y}p(y|0) \nonumber \\&\qquad + \left. \mathbb E _{z}\left. \left[ \frac{\partial }{\partial t} T(Z,0)\right| y,t\right] \right| _{t=0} \partial _{t}^{K_y}p(y|0). \end{aligned}$$

(54)

As $\partial _{t}^{K_y}p(y|t)$ is non-zero, (54) defines the initial derivative $\dot{\mathbb{E }}_{z}\left. \left[ T(Z,0)\right| y,0\right]$. Thus, by selecting $T(Z,t) = Z_i$ we obtain (49) which allows for the calculation of $\dot{\mu }_{i,z}(y,0)$. To obtain (50), we finally choose $T(Z,t) = (Z - \mu _{z}(y,t))^I$.

To determine the initial values using (47)-(50) we evaluate the $(K_y-1)$-th derivatives of $\mathbb E _{z}\left. \left[ (Z+\nu _{j,z})^{e_i} h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)$ and $\mathbb E _{z}\left. \left[ (Z + \nu _{j,z}- \mu _{z}(y,t))^I h_{j}(Z)\right| y-\nu _{j,y},t\right] p(y-\nu _{j,y}|t)$ at $t=0$. Therefore, we merely employ (52) with the appropriate test function $T(Z,t), L = K_y-1$, and the substitution $y \rightarrow y-\nu _{j,y}$. The resulting derivatives are replaced using the same approach and all other conditional expectations are expressed in terms of centered moments using a Taylor series representation similar to (17). While the resulting equation is extremely lengthy, and therefore not stated here, it is straight forward to construct them for any problem using a simple recursion. Employing the structure of (52), it can be shown that the derivatives merely depend on the marginal probabilities and the initial conditional moments of states $\tilde{y}$ with $p(\tilde{y}|0) > 0$. These conditional moments can be computed directly from $p(y,z|0)$, hence, the right-hand sides of (47)–(50) can be evaluated which concludes the proof. $\square$

Some numerical schemes, e.g., DAE solvers based on Taylor series methods, might require higher-order derivatives at the initial time point. These higher-order derivatives can also be constructed using the results of Proposition 5. Therefore, one merely employs (52) with the required order $L$.

Appendix F: Comparison of DAE and approximative ODE formulation of the conditional moment equation

The conditional moment equation is a DAE, $M(\xi ) \dot{\xi } = F(\xi )$, with the state vector $\xi \in \mathbb R ^{n_{\xi }}$ and mass matrix $M(\xi ) \in \mathbb R ^{{n_{\xi }}\times {n_{\xi }}}$. The state vector contains the marginal probabilities, the conditional means and higher-order conditional moments (for $m\ge 2$). The class of DAEs is more general than the class of ODEs, $\dot{\xi } = f(\xi )$. Only if $M(\xi )$ is invertible for all $\xi$ the DAE can be reformulated to an ODE, namely $f(\xi ) = M^{-1}(\xi )F(\xi )$. This invertibility is not ensured for the conditional moment equation. Thus, the conditional moment equation is not an ODE and can also not be simply restated as one.

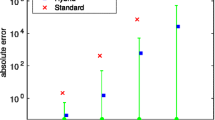
Different approaches exist to approximate DAEs with ODEs. The most common approximation is probably $\dot{\xi } = (M(\xi ) + \delta I)^{-1}F(\xi )$ where $I$ is the identity matrix. The constant $\delta \in \mathbb R _+$ should be as small as possible to achieve a good approximation, but large enough to ensure invertibility. Clearly, even for small $\delta$, the ODE solution is merely an approximation of the DAE solution. To illustrate this we depict in Fig. 13 the error of different methods for the three-stage gene expression model with $y = ([{\hbox {D}}_{\mathrm{off}}],[\hbox {D}_{\mathrm{on}}],[\hbox {R}])$ and $z = [\hbox {P}]$ (see Sect. 5.3). The error is evaluated with respect to the FSP solution which we consider as a gold standard. Figure 13a depicts the error between the FSP solution and the solution of the conditional moment equation computed using a DAE solver. Figure 13b, c depict the error between the FSP solution and the solution of the approximated conditional moment equation, $\dot{\xi } = (M(\xi ) + \delta I)^{-1}F(\xi )$, computed using an ODE solver for $\delta = 10^{-6}$ and $\delta = 10^{-10}$, respectively. It can be seen that the error in the marginal probabilities is small for all three methods, but the error in the conditional moments is indeed very large for the ODE approximations. Interestingly, a smaller $\delta$ results only in a shift of the error into large mRNA numbers, thus small marginal probabilities, but does not decrease the maximal error.

Fig. 13

Error in the marginal probabilities (left) and in the conditional mean of protein number (right) for scenario 2, $\theta ^{(2)}$. The subplots depict the error between the solution of the MCM with $m=2$ computed using different numerical methods and the FSP solution of the CME. The individual lines represent the errors in the conditional means in the off-state (blue solid line), in the on-state (red solid line), and in the overall marginal probabilities (black solid line). (Remark The y-axis scales of the different plots are different.) a DAE solver. b ODE solver with $\delta = 10^{-6}$. c ODE solver with $\delta = 10^{-10}$. d DAE solver with approximated initial conditions ($\delta = 10^{-6}$) (color figure online)

Besides the error introduced by the approximation of the DAE with an ODE, we would like to mention that the reformulation in terms of an ODE might not always be numerically advantageous. DAEs can also be solved for $p(y|t) = 0$, when the corresponding equations provide equality constraints for the dynamic variables. In case of $p(y|t) \ll 1$, the DAE has the advantage that the multiplication by a small value is numerically more stable than the division by a small value. Beyond the simulation of the dynamics, also the treatment of the initial conditions might be critical. For small marginal probabilities $p(y|t)$ the evaluation of (35) and (36) might become numerically unstable. In this situation it can be advantageous to accept a small error in the initial conditions and to use

$$\begin{aligned} \mu _{i,z}(y,0)&= \sum _{z \ge 0} z_i \frac{p(y,z|0)}{p(y|0) + \delta },\\ C_{I,z}(y,0)&= \sum _{z \ge 0} (z - \mu _{z}(y,t))^I \frac{p(y,z|0)}{p(y|0) + \delta }. \end{aligned}$$

As the states for which the error is introduced possess very low marginal probabilities, in our experience the error decays quickly. This is also shown in Fig. 13d, which shows the simulation results obtained using a DAE solver with an approximation of the initial conditions with $\delta = 10^{-6}$.

To sum up, in our experience the simulation of the conditional moment equation using a DAE solver is superior to the approximation of the conditional moment equation by an ODE followed by the simulation of the ODE using ODE solvers. Furthermore, errors introduced in the initial conditional moments of states with lower marginal probabilities in general decay quickly.