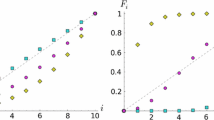
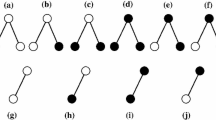
Abstract
Counting processes that keep track of labeled changes to discrete evolutionary traits play critical roles in evolutionary hypothesis testing. If we assume that trait evolution can be described by a continuous-time Markov chain, then it suffices to study the process that counts labeled transitions of the chain. For a binary trait, we demonstrate that it is possible to obtain closed-form analytic solutions for the probability mass and probability generating functions of this evolutionary counting process. In the general, multi-state case we show how to compute moments of the counting process using an eigen decomposition of the infinitesimal generator, provided the latter is a diagonalizable matrix. We conclude with two examples that demonstrate the utility of our results.
Similar content being viewed by others
References
Adachi J. and Hasegawa M. (1996). Model of amino acid substitution in proteins encoded by mitochondrial DNA. J. Mol. Evol. 42: 459–468
Ball F. (1997). Empirical clustering of bursts of openings in Markov and semi-Markov models of single channel gating incorporating time interval omission. Adv. Appl. Probab. 29: 909–946
Ball F. and Milne R.K. (2005). Simple derivations of properties of counting processes associated with Markov renewal processes. J. Appl. Probab. 42: 1031–1043
Chatfield C. (2004). The Analysis of Time Series: An Introduction. Chapman & Hall, London
Darroch J.N and Morris K.W. (1967). Some passage-time generating functions for discrete-time and continuous-time finite Markov chains. J. Appl. Probab. 4: 496–507
Felsenstein J. (1981). Evolutionary trees from DNA sequences: a maximum likelihood approach. J. Mol. Evol. 13: 93–104
Felsenstein J. (2004). Inferring Phylogenies. Sinauer Associates Inc., Sunderland
Fitch W.M., Bush R.M., Bender C.A. and Cox N.J. (1997). Long term trends in the evolution of H(3) HA1 human influenza type A. Proc. Natl. Acad. Sci. USA 94: 7712–7718
Guttorp P. (1995). Stochastic Modeling of Scientific Data. Chapman & Hall, Suffolk
Hasegawa M., Kishino H. and Yano T. (1985). Dating the human-ape splitting by a molecular clock of mitochondrial DNA. J. Mol. Evol. 22: 160–174
Henikoff S. and Henikoff J.G. (1992). Amino acid substitution matrices from protein blocks. Proc. Natl. Acad. Sci. USA 89: 10915–10919
Hobolth, A., Jensen, J.L.: Statistical inference in evolutionary models of DNA sequences via the EM algorithm. Stat. Appl. Gen. Mol. Biol. 4, Article 18 (2005)
Kass R.E. and Raftery A.E. (1995). Bayes factors. J. Am. Stat. Assoc. 90: 773–795
Meng X.L. (1994). Posterior predictive P-values. Ann. Stat. 22: 1142–1160
Narayana S. and Neuts M.F. (1992). The first two moment matrices of the counts for the Markovian arrival process. Stoch. Models 8: 459–477
Neuts M.F. (1979). A versatile Markovian point process. J. Appl. Probab. 16: 764–779
Neuts M.F. (1992). Models based on the Markovian arrival process. IEICE Trans. Commun. E75-B: 1255–1265
Neuts M.F. (1995). Algorithmic Probability: a Collection of Problems. Chapman and Hall, London
Nielsen R. (2002). Mapping mutations on phylogenies. Syst. Biol. 51: 729–739
Nielsen R. (2005). Molecular signatures of natural selection. Ann. Rev. Gen. 39: 197–218
Oakley T.H. and Cunningham C.W. (2002). Molecular phylogenetic evidence for the independent evolutionary origin of an arthropod compound eye. Proc. Natl. Acad. Sci. USA 99: 1426–1430
Pagel M. (1994). Detecting correlated evolution on phylogenies: a general method for the comparative analysis of discrete characters. Proc. R. Soc. B 255: 37–45
Pagel M. (1999). The maximum likelihood approach to reconstructing ancestral character states of discrete characters on phylogenies. Syst. Biol. 48: 612–622
Pollock D.D., Taylor W.R. and Goldman N. (1999). Coevolving protein residues: maximum likelihood identification and relationship to structure. J. Mol. Biol. 287: 187–198
Rambaut A. and Grassly N.C. (1997). Seq-Gen: An application for the Monte Carlo simulation of DNA sequence evolution along phylogenetic trees. Comput. Appl. Biosci. 13: 235–238
Schadt E. and Lange K. (2002). Codon and rate variation models in molecular phylogeny. Mol. Biol. Evol. 19: 1534–1549
Schadt E.E., Sinsheimer J.S. and Lange K. (1998). Computational advances in maximum likelihood methods for molecular phylogeny. Genome Res. 8: 222–233
Siepel, A., Pollard, K.S., Haussler, D.: New methods for detecting lineage-specific selection. In: Proceedings of the 10th international conference on research in computational molecular biology, pp. 190–205 (2006)
Suchard M.A., Weiss R.E., Dorman K.S. and Sinsheimer J.S. (2002). Inferring spatial phylogenetic variation along nucleotide sequences: a multiple change-point model. J. Am. Stat. Assoc. 98: 427–437
Templeton A.R. (1996). Contingency tests of neutrality using intra/interspecific gene trees: the rejection of neutrality for the evolution of the mitochondrial cytochrome oxidase II gene in the hominoid primates. Genetics 144: 1263–1270
Yang Z. (1994). Maximum likelihood phylogenetic estimation from DNA sequences with variable rates over sites: approximate methods. J. Mol. Evol. 39: 306–314
Yang Z. (1995). A space-time process model for the evolution of DNA sequences. Genetics 139: 993–1005
Yang Z., Nielsen R., Goldman N. and Pedersen A.M.K. (2000). Codon-substitution models for heterogeneous selection pressure at amino acid sites. Genetics 155: 431–449
Zheng Q. (2001). On the dispersion index of a Markovian molecular clock. Math. Biosci. 172: 115–128
Author information
Authors and Affiliations
Corresponding author
Additional information
V.N.M. was supported by a Dissertation Year Fellowship from the UCLA Graduate Division. M.A.S. is an Alfred P. Sloan Research Fellow.
Rights and permissions
About this article
Cite this article
Minin, V.N., Suchard, M.A. Counting labeled transitions in continuous-time Markov models of evolution. J. Math. Biol. 56, 391–412 (2008). https://doi.org/10.1007/s00285-007-0120-8
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00285-007-0120-8