Skip to main content
SpringerLink
Log in

Fractional modelling of Pennes’ bioheat transfer equation

  • Original
  • Published:
Heat and Mass Transfer Aims and scope Submit manuscript

Abstract

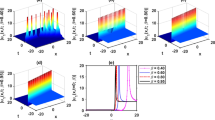
A new mathematical model for Pennes’ bioheat equation using the methodology of fractional calculus was constructed. The thermal behavior in living tissue subjected to instantaneous surface heating was investigated. Numerical calculations were performed to study the temperature transients in the skin exposed to instantaneous surface heating. Some comparisons were shown in figures to estimate the effect the fractional order parameter α on the thermal wave. In this novel theory, the fractional parameter α is an indicator of bioheat efficiency in living tissues.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Zhao J, Zhang J, Kang N, Yang F (2005) A two level finite difference scheme for one dimensional Pennes’ bioheat equation. Appl Math Comput 171:320–331

    Article  MATH  MathSciNet  Google Scholar 

  2. Pennes HH (1948) Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol 1:93–122

    Google Scholar 

  3. Wissler EH (1948) Pennes’ 1948 model paper revisited. J Appl Physiol 85:36–42

    Google Scholar 

  4. Cundin LX, Roach WP, Millenbaugh N (2009) Empirical comparison of Pennes’ bio-heat equation. Proc SPIE 7175:717516–717519

    Article  Google Scholar 

  5. Vernotte P (1958) Les Paradoxes de la theorie continue de l’equation de la chaleur. Compte Rendus 246:3154–3155

    MathSciNet  Google Scholar 

  6. Cattaneo C (1958) A form of heat conduction equation which eliminates the paradox of instantaneous propagation. Compte Rendus 247:431–433

    MathSciNet  Google Scholar 

  7. Kaminski W (1990) Hyperbolic heat conduction equation for material with a non-homogeneous inner structure. ASME J Heat Transfer 112:555–560

    Article  Google Scholar 

  8. Mitra K, Kumar S, Vedevarz A, Moallemi MK (1995) Experimental evidence of hyperbolic heat conduction in processed meat. J Heat Transfer 117:568–573

    Article  Google Scholar 

  9. Liu J (2000) Preliminary survey on the mechanisms of the wave-like behaviors of heat transfer in living tissues. Forsch Ing 66:1–10

    Article  Google Scholar 

  10. Abel NH (1926) Solutions de quelques problèmes à l’aide d’intégrales defines, Oeuvres complètes, nouvelle éd., 1, Grondahl & Son, Christiania (1881) pp 11–27 (Edition de Holmboe)

  11. Povstenko YZ (2012) Neumann boundary-value problems for a time-fractional diffusion-wave equation in a half-plane. Comput Math Appl 64:3183–3192

    Article  MATH  MathSciNet  Google Scholar 

  12. Caputo M (1967) Linear models of dissipation whose Q is almost frequency independent II. Geophys J R Astron Soc 13:529–539

    Article  Google Scholar 

  13. Kiryakova V (1994) Generalized fractional calculus and applications. In: Pitman Res Notes Math Ser, vol 301. Longman-Wiley, New York

  14. Podlubny I (1999) Fractional differential equations. Academic Press, New York

    MATH  Google Scholar 

  15. Jumarie GD (2010) Derivation and solutions of some fractional Black–Scholes equations in coarse-grained space and time, application to Merton’s optimal portfolio. Comput Math Appl 59:1142–1164

    Article  MATH  MathSciNet  Google Scholar 

  16. Ezzat MA (2010) Thermoelectric MHD non-Newtonian fluid with fractional derivative heat transfer. Phys B 405:4188–4194

    Article  Google Scholar 

  17. Ezzat MA (2011) Magneto-thermoelasticity with thermoelectric properties and fractional derivative heat transfer. Phys B 406:30–35

    Article  Google Scholar 

  18. Mainardi F, Gorenflo R (2000) On Mittag–Lettler-type function in fractional evolution processes. J Comput Appl Math 118:283–299

    Article  MATH  MathSciNet  Google Scholar 

  19. Lord H, Shulman Y (1967) A generalized dynamical theory of thermoelasticity. J Mech Phys Solids 15:299–309

    Article  MATH  Google Scholar 

  20. Lebon G, Jou D, Casas-Vázquez J (2008) Understanding non-equilibrium thermodynamics: foundations, applications, frontiers. Springer, Berlin

    Book  Google Scholar 

  21. Jou D, Casas-Vázquez J, Lebon G (1988) Extended irreversible thermodynamics. Rep Prog Phys 51:1105–1179

    Article  Google Scholar 

  22. Ozisik MN, Tzou DY (1994) On the wave theory in heat conduction. J Heat Transfer 116:526–535

    Article  Google Scholar 

  23. Povstenko YZ (2005) Fractional heat conduction and associated thermal stress. J Thermal Stress 28:83–102

    Article  MathSciNet  Google Scholar 

  24. Ichkawa S, Kishima A (1972) Application of Fourier series technique to inverse Laplace transform. Kyoto University Memoirs, Kyoto University, Japan 34:53–67

    Google Scholar 

  25. Honig G, Hirdes U (1984) A method for the numerical inversion of the Laplace transform. J Comput Appl Math 10:113–132

    Article  MATH  MathSciNet  Google Scholar 

  26. Luisiana CX, William PR, Nancy M (2009) Empirical comparison of Pennes’ bio-heat equation. Proc SPIE 7175:717516

    Article  Google Scholar 

  27. Shih TC, Kou HS, Liauh CT, Win WL (2005) The impact of thermal wave characteristics on thermal does distribution during thermal therapy, a numerical study. Med Phys 32:3029–3036

    Article  Google Scholar 

  28. Sharma PR, Sazid A, Katiyar VK (2009) Numerical study of heat propagation in living tissue subjected to instantaneous heating. Ind J Biomech 7–8:205–209

    Google Scholar 

  29. Shen W, Zhang J (2005) Modeling and numerical simulation of bioheat transfer and biomechanics in soft tissue. Math Comput Model 41:1251–1265

    Article  MATH  MathSciNet  Google Scholar 

  30. Liu J, Chen X, Xu LX (1999) New thermal wave aspects on burn evaluation of skin subjected to instantaneous heating. IEEE Trans Biomed Eng 46:420–428

    Article  Google Scholar 

  31. Weymann HD (1967) Finite speed of propagation in heat conduction, diffusion, and viscous shear motion. Am J Phys 35:488–496

    Article  Google Scholar 

  32. Shih TC, Yuan P, Lin WL, Kou HS (2007) Analytical analysis of the Pennes bioheat transfer equation with sinusoidal heat flux condition on skin surface. Med Eng Phys 29:946–953

    Article  Google Scholar 

  33. PovstenkoYZ (2013) Fundamental solutions to time-fractional heat conduction equations in two joint half-lines. Cent Euro J Phys. doi:10.2478/s11534-013-0272-7

Download references

Author information

Author notes

  1. Magdy A. Ezzat

    Present address: Department of Mathematics, Faculty of Sciences and Letters in Al Bukayriyyah, Qassim University, Qassim, Saudi Arabia

Authors and Affiliations

  1. Department of Mathematics, Faculty of Education, Alexandria University, Alexandria, Egypt

    Magdy A. Ezzat

  2. Department of Mathematics, Faculty of Sciences and Letters in Al Bukayriyyah, Qassim University, Qassim, Saudi Arabia

    Shereen M. Ezzat

  3. Department of Biology, Faculty of Science, Qassim University, Buraydah, 51452, Saudi Arabia

    Noorah S. AlSowayan

  4. Department of Mathematics, Faculty of Science, Qassim University, Buraydah, 51452, Saudi Arabia

    Zeid I. A. Al-Muhiameed

Authors
  1. Magdy A. Ezzat
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Noorah S. AlSowayan
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Zeid I. A. Al-Muhiameed
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Shereen M. Ezzat
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Magdy A. Ezzat.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Ezzat, M.A., AlSowayan, N.S., Al-Muhiameed, Z.I.A. et al. Fractional modelling of Pennes’ bioheat transfer equation. Heat Mass Transfer 50, 907–914 (2014). https://doi.org/10.1007/s00231-014-1300-x

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s00231-014-1300-x

Keywords

Search

Navigation