Abstract
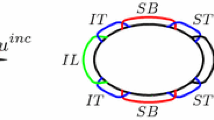
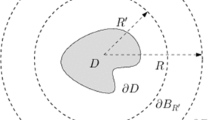
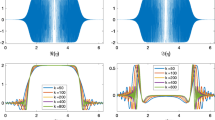
In this paper we propose and analyse a hybrid numerical-asymptotic boundary element method for the solution of problems of high frequency acoustic scattering by a class of sound-soft nonconvex polygons. The approximation space is enriched with carefully chosen oscillatory basis functions; these are selected via a study of the high frequency asymptotic behaviour of the solution. We demonstrate via a rigorous error analysis, supported by numerical examples, that to achieve any desired accuracy it is sufficient for the number of degrees of freedom to grow only in proportion to the logarithm of the frequency as the frequency increases, in contrast to the at least linear growth required by conventional methods. This appears to be the first such numerical analysis result for any problem of scattering by a nonconvex obstacle. Our analysis is based on new frequency-explicit bounds on the normal derivative of the solution on the boundary and on its analytic continuation into the complex plane.













Similar content being viewed by others
References
Chandler-Wilde, S.N., Graham, I.G., Langdon, S., Spence, E.A.: Numerical-asymptotic boundary integral methods in high-frequency acoustic scattering. Acta Numer. 21, 89–305 (2012)
Hewett, D.P., Langdon, S., Melenk, J.M.: A high frequency \(hp\) boundary element method for scattering by convex polygons. SIAM J. Numer. Anal. 51, 629–653 (2013)
Babic̆ V.M., Buldyrev, V.S.: Short-Wavelength Diffraction Theory. Springer, Berlin (1991)
Borovikov, V.A., Kinber, B.Y.: Geometrical Theory of Diffraction, IEE Electromagnetic Waves Series, vol. 37. Institution of Electrical Engineers (IEE), London (1994)
Bouche, D., Molinet, F., Mittra, R.: Asymptotic Methods in Electromagnetics. Springer, New York (1997)
Keller, J.B.: Geometrical theory of diffraction. J. Opt. Soc. Am. A 52, 116–130 (1962)
Kouyoumjian, R.G., Pathak, P.H.: A uniform geometrical theory of diffraction for an edge in a perfectly conducting surface. P. IEEE 62(11), 1448–1461 (1974)
Rawlins, A.D.: High-frequency diffraction of a electromagnetic plane wave by an imperfectly conducting rectangular cylinder. J. Eng. Math. 76, 157–180 (2012)
Chandler-Wilde, S.N., Langdon, S.: A Galerkin boundary element method for high frequency scattering by convex polygons. SIAM J. Numer. Anal. 45(2), 610–640 (2007)
Chandler-Wilde, S.N., Langdon, S., Mokgolele, M.: A high frequency boundary element method for scattering by convex polygons with impedance boundary conditions. Commun. Comput. Phys. 11, 573–593 (2012)
Betcke, T., Spence, E.A.: Numerical estimation of coercivity constants for boundary integral operators in acoustic scattering. SIAM J. Numer. Anal. 49(4), 1572–1601 (2011)
Chandler-Wilde, S.N., Graham, I.G., Langdon, S., Lindner, M.: Condition number estimates for combined potential boundary integral operators in acoustic scattering. J. Integral Equ. Appl. 21(2), 229–279 (2009)
Bruno, O.P.: Fast, high-order, high-frequency integral methods for computational acoustics and electromagnetics. In: Topics in Computational Wave Propagation, Lect. Notes Comput. Sci. Eng., vol. 31, pp. 43–82. Springer (2003)
Bruno, O.P., Reitich, F.: High order methods for high-frequency scattering applications. In: H. Ammari (ed.) Modeling and Computations in Electromagnetics, Lect. Notes Comput. Sci. Eng., vol. 59, pp. 129–164. Springer (2007)
Chandler-Wilde, S.N., Hewett, D.P., Langdon, S., Twigger, A.: A high frequency BEM for scattering by non-convex obstacles. In: Proceedings of 10th Int. Conf. on Mathematical and Numerical Aspects of Waves, Vancouver, Canada, pp. 307–310 (2011)
Anand, A., Boubendir, Y., Ecevit, F., Reitich, F.: Analysis of multiple scattering iterations for high-frequency scattering problems. II: the three-dimensional scalar case. Numer. Math. 114(3), 373–427 (2010)
Ecevit, F.: Integral equation formulations of electromagnetic and acoustic scattering problems: convergence of multiple scattering interations and high-frequency asymptotic expansions. Ph.D. thesis, University of Minnesota (2005)
Ecevit, F., Reitich, F.: Analysis of multiple scattering iterations for high-frequency scattering problems. Part I: the two-dimensional case. Numer. Math. 114, 271–354 (2009)
Geuzaine, C., Bruno, O., Reitich, F.: On the O(1) solution of multiple-scattering problems. IEEE Trans. Magn. 41, 1488–1491 (2005)
Colton, D., Kress, R.: Inverse Acoustic and Electromagnetic Scattering Theory. Springer, Berlin (1992)
Colton, D.L., Kress, R.: Integral Equation Methods in Scattering Theory. Wiley, New York (1983)
Betcke, T., Chandler-Wilde, S.N., Graham, I.G., Langdon, S., Lindner, M.: Condition number estimates for combined potential boundary integral operators in acoustics and their boundary element discretisation. Numer. Methods PDEs 27(1), 31–69 (2011)
Kress, R.: Minimizing the condition number of boundary integral operators in acoustic and electromagnetic scattering. Quart. J. Mech. Appl. Math. 38(2), 323 (1985)
Spence, E.A., Chandler-Wilde, S.N., Graham, I.G., Smyshlyaev, V.P.: A new frequency-uniform coercive boundary integral equation for acoustic scattering. Comm. Pure Appl. Math. 64(10), 1384–1415 (2011)
Chandler-Wilde, S.N., Monk, P.: Wave-number-explicit bounds in time-harmonic scattering. SIAM J. Math. Anal. 39(5), 1428–1455 (2008)
Domínguez, V., Graham, I.G., Smyshlyaev, V.P.: A hybrid numerical-asymptotic boundary integral method for high-frequency acoustic scattering. Numer. Math. 106(3), 471–510 (2007)
Spence, E.A., Kamotski, I.V., Smyshlyaev, V.P.: Coercivity of combined boundary integral equations in high-frequency scattering. Comm. Pure Appl. Math. (2014). http://people.bath.ac.uk/eas25/SpKaSm13.pdf
Oberhettinger, F.: On asymptotic series for functions occuring in the theory of diffraction of waves by wedges. J. Math. Phys. 34, 245–255 (1956)
Bowman, J.J., Senior, T.B.A., Uslenghi, P.L.E.: Electromagnetic and acoustic scattering by simple shapes. Hemisphere Publishing Corp, New York (1987)
Digital Library of Mathematical Functions. National Institute of Standards and Technology. http://dlmf.nist.gov/. Released 7 May 2010
Titchmarsh, E.C.: Theory of Functions, 2nd edn. OUP, London (1939)
Chandler-Wilde, S.N.: Boundary value problems for the Helmholtz equation in a half-plane. In: Proceedings of Third Int. Conf. on Mathematical and Numerical Aspects of Wave Propagation, pp. 188–197. SIAM (1995)
Schwab, C.: \(p-\) and \(hp-\) Finite Element Methods. Clarendon Press, Oxford (1998)
Stenger, F.: Numerical Methods Based on Sinc and Analytic Functions. Springer, New York (1993)
Twigger, A.: Boundary element methods for high frequency scattering. Ph.D. thesis, University of Reading (2013)
Alazah, M., Chandler-Wilde, S.N., La Porte, S.: Computing Fresnel integrals via modified trapezium rules. Numer. Math. (2014). doi:10.1007/s00211-014-0627-z
Groth, S.P., Hewett, D.P., Langdon, S.: Hybrid numerical-asymptotic approximation for high frequency scattering by penetrable convex polygons. IMA J. Appl. Math. (2014). doi:10.1093/imamat/hxt040
Acknowledgments
The authors thank the editor and the anonymous reviewers for their helpful comments, and acknowledge funding support from EPSRC (EP/F067798/1 to S.N.C-W., D.P.H. and S.L., and DTG studentship to A.T.).
Author information
Authors and Affiliations
Corresponding author
Additional information
Supported by EPSRC grant EP/F067798/1.
Rights and permissions
About this article
Cite this article
Chandler-Wilde, S.N., Hewett, D.P., Langdon, S. et al. A high frequency boundary element method for scattering by a class of nonconvex obstacles. Numer. Math. 129, 647–689 (2015). https://doi.org/10.1007/s00211-014-0648-7
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s00211-014-0648-7