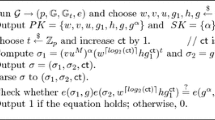Confined Guessing: New Signatures From Standard Assumptions

Abstract

We put forward a new technique to construct very efficient and compact signature schemes. Our technique combines several instances of only a mildly secure signature scheme to obtain a fully secure scheme. Since the mild security notion we require is much easier to achieve than full security, we can combine our strategy with existing techniques to obtain a number of interesting new (stateless and fully secure) signature schemes. Concretely, we get (1) A scheme based on the computational Diffie–Hellman (CDH) assumption in pairing-friendly groups. Signatures contain $\mathbf {O}(1)$ and verification keys $\mathbf {O}(\log k)$ group elements, where $k$ is the security parameter. Our scheme is the first fully secure CDH-based scheme with such compact verification keys. (2) A scheme based on the (nonstrong) RSA assumption in which both signatures and verification keys contain $\mathbf {O}(1)$ group elements. Our scheme is significantly more efficient than existing RSA-based schemes. (3) A scheme based on the Short Integer Solutions (SIS) assumption. Signatures contain $\mathbf {O}(\log (k)\cdot m)$ and verification keys $\mathbf {O}(n\cdot m) {\mathbb {Z}}_p$-elements, where $p$ may be polynomial in $k$, and $n,m$ denote the usual SIS matrix dimensions. Compared to state-of-the-art SIS-based schemes, this gives very small verification keys, at the price of slightly larger signatures. In all cases, the involved constants are small, and the arising schemes provide significant improvements upon state-of-the-art schemes. The only price we pay is a rather large (polynomial) loss in the security reduction. However, this loss can be significantly reduced at the cost of an additive term in signature and verification key size.

1 Introduction

Generic and Non-generic Signature Schemes Digital signature schemes can be built from any one-way function [24, 27, 28]. However, this generic construction is not particularly efficient. (For instance, each signature contains $\mathbf {O}(k^2)$ preimages.) One could hope that for concrete assumptions (such as the RSA or Diffie–Hellman-related assumptions), it is possible to derive much more efficient schemes.

Tree-Based Signatures Although indeed there exists a variety of efficient signature schemes from concrete assumptions, there are surprisingly few different technical paradigms. For instance, early RSA-based signature schemes (such as [11, 12, 16]) follow a tree-based approach, much similar to the generic construction from [27, 28]. Also later schemes (e.g., [13] and its variants [14, 17, 22], or [20]) can at least be seen as heavily inspired by earlier tree-based schemes. For instance, [13] can be seen as a more efficient variant of the scheme from [12] with an extremely flat tree, at the price of a stronger computational assumption. On the other hand, the scheme from [20] can be viewed as a tree-based scheme in which signatures are aggregated and thus become very compact.

Partitioning Strategies A second class of signature schemes tries to enable a “partitioning strategy” during the security proof (e.g., [6, 9, 17, 34]). (This means that during the security proof, the set of messages is partitioned into those that can be signed by the simulator, and those that cannot.) At least outside of the random oracle model, currently known instantiations of partitioning strategies rely on certain algebraic structures, and lead to comparatively large public keys.

More Specific Schemes Finally, there are a number of very efficient signature schemes (e.g., [5, 33]) with specific requirements. For instance, the scheme of [5] relies on a specific (and somewhat nonstandard) computational assumption, and the scheme of [33] inherently requires a decisional (as opposed to a search) assumption. While we focus on the standard model, we note that there are also very efficient schemes with a heuristic proof, i.e., a proof in the random oracle model (e.g., [2]).

1.1 Our Contribution

In this work, we present a new paradigm for the construction of efficient signature schemes from standard computational assumptions.

The Technical Difficulty We believe that one of the main difficulties in constructing signature schemes is the following. Namely, in the standard security experiment for digital signatures, an adversary $A$wins if it generates a signature for a (fresh) message of his own choice. If we use $A$in a straightforward way as a problem-solver in a security reduction to a computational assumption, then $A$itself may select which instance of the particular problem it is going to solve (by choosing the forgery message). Note that we cannot simply guess which instance $A$is going to solve, since there usually will be superpolynomially many possible messages (and thus problem instances).¹

Our Main Idea We now explain the main idea behind our approach. As a stepping stone, we introduce a very mild form of security for signature schemes that is much easier to achieve than full (i.e., standard) security. Intuitively, the mild security experiment forces an adversary to essentially commit to a crucial part of the forgery before even seeing the verification key. During a security reduction, this allows us to embed a computational problem into the verification key that is tailored specifically to the adversary’s forgery. In particular, we do not have to rely on strong assumptions to achieve mild security. Indeed, we present very efficient mildly secure schemes based on the computational Diffie–Hellman (CDH) assumption (in pairing-friendly groups), the RSA assumption, and the Short Integer Solutions (SIS) assumption. These constructions are basically stripped-down versions of known (fully secure) stateful [21] and stateless [6] schemes.

The heart of our work is a very simple and efficient construction of a fully secure signature scheme from $\log (k)$ instances of a mildly secure one. Note that we only use logarithmically many mildly secure instances. In contrast, the related—but technically very different—prefix-guessing technique of Hohenberger and Waters [7, 20, 27], uses $k$ instances of a “less secure” scheme. Furthermore, the signature schemes that result from our transformation can often be optimized (e.g., using aggregation of signatures or verification keys). Concretely, if we use our transformation on the mildly secure schemes mentioned above, and optimize the result, then we end up with extremely efficient new signature schemes from standard assumptions.

More on Our Techniques We now explain our transformation in a little more detail. We start out with a tag-based signature scheme that satisfies only a very mild form of security. In a tag-based signature scheme, signatures carry a tag $t$that can be chosen freely during signature time. In our mild security experiment, the adversary $A$must initially (i.e., nonadaptively) specify all messages $M_i$ it wants signed, along with corresponding pairwise different tags $t_i$. After receiving the verification key and the requested signatures, $A$is then expected to forge a signature for a fresh message $M^*$, but with respect to a “recycled” tag $t^*=t_i$ (that was already used for one of the initially signed messages).

Mild security thus forces $A$to choose the tag $t^*$ of his forgery from a small set $\{t_i\}_i$ of possible tags. In a security proof, we can simply guess $t^*=t_i$ with significant probability, and embed a computational problem that is specifically tailored toward $t^*$ into the verification key.² How this embedding is done depends on the specific setting; for instance, in the CDH setting, $t^*$ can be used to program a Boneh–Boyen hash function [4]. In fact, Hohenberger and Waters [21] use such a programming to construct a very efficient stateful signature scheme.

A signature in our fully secure scheme consists of $\log (k)$ signatures $(\sigma _i)_{i=1}^{\log (k)}$ of a mildly secure scheme. (In some cases, these signatures can be aggregated.) The $i$-th signature component $\sigma _i$ is created with tag chosen as uniform $2^i$-bit string. Hence, tag-collisions (i.e., multiply-used tags) are likely to occur after a few signatures in instances with small $i$, while instances with larger $i$ will almost never have tag-collisions.

We will reduce the (full) security of the new scheme generically to the mild security of the underlying scheme. When reducing a concrete (full) adversary $B$to a mild adversary $A$, we will first single out an instance $i^*$ such that (a) the set of all tags is polynomially small (so we can guess the $i^*$-th challenge tag $t_{i^*}^*$ in advance), and (b) tag-collisions occur only with sufficiently small (but possibly nonnegligible) probability in an attack with $A$(so only a constant number of $t_{i^*}^*$-signatures will have to be generated for $A$). This instance $i^*$ is the challenge instance, and all other instances are simulated by $A$for $B$.³ Any valid forgery of $B$ must contain a valid signature under instance $i^*$ with $2^{i^*}$-bit tag. Hence, any $B$-forgery implies an $A$-forgery.

The bottleneck of our transformation is the security reduction. Concretely, if $B$makes $q$ signature queries and forges with success probability $\varepsilon$, then $A$will make up to $Q=\mathbf {O}(q^4/\varepsilon )$ signature queries and have success $\varepsilon /2$. (One “squaring” is caused by a birthday bound when hoping for few tag-collisions; another squaring may occur when we have to round $i^*$ up to the next integer.) This security loss is annoying, but can be significantly reduced by using techniques from [17]. In other words, by first applying a suitable “weakly programmable” hash function to tags, we can allow $m$-fold tag-collisions in the signatures prepared for $B$, at the cost of an extra $m$ group elements in verification key and signatures. Orthogonally, we can use $c^i$-bit tags with $1<c<2$ (instead of $2^i$-bit tags) in the $i$-th mildly secure instance to get a “finer-grained” growth of possible tag sets. This costs a multiplicative factor of $1/\log _2(c)$ in verification key and signature size, unless of course aggregation is possible. With these measures, the security reduction improves considerably: $A$will make $Q=\mathbf {O}(q^{c+c/m}/\varepsilon ^{c/m})$ signature queries and have success $\varepsilon /2$. Varying $c$ and $m$ gives thus an interesting tradeoff between efficiency and quality of the security reduction.

Efficiency Comparison The most efficient previous CDH-based signature scheme [34] has signatures and public keys of size $\mathbf {O}(1)$, resp. $\mathbf {O}(k)$ group elements. Our CDH-based scheme also has constant-sized signatures, and more compact public keys. Concretely, we can get public keys of $\mathbf {O}(\log (k))$ group elements at the price of a worse security reduction. Our RSA-based scheme has similar key and signature sizes as existing RSA-based schemes [18, 20], but requires significantly fewer (i.e., only $\mathbf {O}(\log (k))$ instead of $\mathbf {O}(k)$, resp. $\mathbf {O}(k/\log (k))$ many) generations of large primes. Again, this improvement is bought with a worse security reduction. Our SIS-based scheme offers an alternative to the existing scheme of [6]. Concretely, our scheme has larger (by a factor of $\log (k)$) signatures and a worse security reduction, but significantly smaller (by a factor of $k/\log (k)$) public keys.

On a Related Result by Seo In an independent work, Seo [30] constructs essentially the same CDH-based scheme, however, with a very different security analysis. His analysis is much tighter than ours, and for concrete security parameters, his scheme is more efficient. At the same time, Seo only proves a bounded form of security in which the number of adversarial signature queries has to be known at the time of key generation. The merged paper [3] presents both his and our own analysis.

2 Preliminaries

Notation For $n\in {\mathbb {R}}$, let $[n]\,{:=}\,\{1,\ldots ,\lfloor n\rfloor \}$. Throughout the paper, $k\in {\mathbb {N}}$ denotes the security parameter. For a finite set $\mathcal {S}$, we denote by $s\leftarrow \mathcal {S}$ the process of sampling $s$ uniformly from $\mathcal {S}$. For a probabilistic algorithm $A$, we write $y\leftarrow A(x)$ for the process of running $A$on input $x$ with uniformly chosen random coins, and assigning $y$ the result. If $A$’s running time is polynomial in $k$, then $A$ is called probabilistic polynomial-time (PPT). A function $f:{\mathbb {N}}\rightarrow {\mathbb {R}}_{\ge 0}$ is negligible if it vanishes faster than the inverse of any polynomial (i.e., if $\forall c\exists k_0\forall k\ge k_0: f(k)\le 1/k^c$). On the other hand, $f$ is significant if it dominates the inverse of some polynomial (i.e., if $\exists c,k_0\forall k\ge k_0: f(k)\ge 1/k^c$).

Definition 2.1.

(Signature scheme) A signature scheme $\mathsf {SIG}$with message space $\mathcal {M}_k$ consists of three PPT algorithms:

• Setup The setup algorithm $\mathsf {Gen}(1^k)$, given the security parameter $1^k$ in unary, outputs a public key $pk$and a secret key $sk$.

• Sign The signing algorithm $\mathsf {Sig}( sk ,M)$, given the secret key $sk$and a message $M\in \mathcal {M}_k$, outputs a signature $\sigma$.

• Verify Given the public key $pk$, a message $M$, and a signature $\sigma$, $\mathsf {Ver}( pk ,M,\sigma )$ outputs a bit $b\in \left\{ 0,1\right\}$. (The case $b=1$ corresponds to a valid signature on the message, and the case $b=0$ means invalid.)

For correctness, we require for any $k\in {\mathbb {N}}$, all $( pk , sk )\leftarrow \mathsf {Gen}(1^k)$, all $M\in \mathcal {M}_k$, and all $\sigma \leftarrow \mathsf {Sig}( sk ,M)$ that $\mathsf {Ver}( pk ,M,\sigma )=1$.

Definition 2.2.

(Distinct-message) existential unforgeability under (non-adaptive) chosen-message attacks). We say a signature scheme is existential unforgeable under chosen-message attacks (EUF-CMA) or existential unforgeable under distinct-message non-adaptive chosen-message attacks (EUF-dnaCMA) iff

$$\begin{aligned} \mathsf {Adv}^{\mathsf {euf\text{- }cma}}_{\mathsf {SIG},F}(k) \,&:= \, \Pr \left[ {\mathsf {Exp}^{\mathsf {euf\text{- }cma}}_{\mathsf {SIG},F}(k)=1}\right] \text { and } \\ \mathsf {Adv}^{\mathsf {euf\text{- }dnacma}}_{\mathsf {SIG},F}(k)\,&:= \, \Pr \left[ {\mathsf {Exp}^{\mathsf {euf\text{- }dnacma}}_{\mathsf {SIG},F}(k)=1}\right] , \end{aligned}$$

respectively, are negligible for any PPT adversary $F$, where $\mathsf {Exp}^{\mathsf {euf\text{- }cma}}_{\mathsf {SIG},F} (k)$ and $\mathsf {Exp}^{\mathsf {euf\text{- }dnacma}}_{\mathsf {SIG_{t}},F}(k)$, respectively, are defined in Fig. 1.

Fig. 1

EUF-CMA and EUF-dnaCMA experiments for signature schemes

Pseudorandom Functions For any set $\mathcal {S}$, a pseudorandom function (PRF) with range $\mathcal {S}$is an efficiently computable function: $\mathsf {PRF}^\mathcal {S}:\left\{ 0,1\right\} ^k\times \left\{ 0,1\right\} ^* \rightarrow \mathcal {S}$. We may also write $\mathsf {PRF}^\mathcal {S}_\kappa (x)$ for $\mathsf {PRF}^\mathcal {S}(\kappa ,x)$ with key $\kappa \in \{0,1\}^k$. In addition, we require that

$$\begin{aligned} \mathsf {Adv}^{\mathsf {prf}}_{\mathsf {PRF}^\mathcal {S}, A}(k) \,{:=}\, \left| \Pr \left[ {A^{\mathsf {PRF}^\mathcal {S}_\kappa (\cdot )} = 1 \text { for } \kappa \leftarrow \{0,1\}^k}\right] - \Pr \left[ {A^{\mathcal {U}_\mathcal {S}(\cdot )} = 1}\right] \right| \end{aligned}$$

is negligible in $k$ where $\mathcal {U}_\mathcal {S}$ is a truly uniform function to $\mathcal {S}$. Note that for any efficiently samplable set $\mathcal {S}$with uniform sampling algorithm $\mathsf {Samp}$, we can generically construct a PRF with range $\mathcal {S}$from a PRF $\mathsf {PRF}^{\{0,1\}^k}$ by using the output of $\mathsf {PRF}^{\{0,1\}^k}_\kappa$ as random coins for $\mathsf {Samp}$. Following this principle, we can construct $(\mathsf {PRF}^{\mathcal {S}_i})_{i \in [n]}$ for a family of sets $(\mathcal {S}_i)_{i \in [n]}$ from a single PRF $\mathsf {PRF}^{\{0,1\}^k}$ with sufficiently long output (hence, we need only one key $\kappa$).

Chameleon Hashing A chameleon hash scheme consists of two PPT algorithms $(\mathsf {CHGen},$ $\mathsf {CHTrapColl})$. $\mathsf {CHGen}(1^k)$ outputs a tuple $(\mathsf {CH},\tau )$ where $\mathsf {CH}$ is the description of a efficiently computable chameleon hash function $\mathsf {CH}:\mathcal {M}\times \mathcal {R}\rightarrow \mathcal {N}$ which maps a message $M$and randomness $r$to a hash value $\mathsf {CH}(M,r)$. We require collision-resistance in the sense that it is infeasible to find $(M,r)\ne (M',r')$ with $\mathsf {CH}(M,r) = \mathsf {CH}(M',r')$. However, the trapdoor $\tau$allows us to produce collisions in the following sense: given arbitrary $M,r,M'$, $\mathsf {CHTrapColl}(\tau , M, r, M')$ finds $r'$ with $\mathsf {CH}(M,r) = \mathsf {CH}(M',r')$. We require that the distribution of $r'$ is uniform given only $\mathsf {CH}$and $M'$.

3 Tag-Based Signatures: From Mild to Full Security

We now describe our main result: a generic transformation from mildly secure tag-based signature schemes to fully secure schemes. Let us first define the notion of tag-based signature schemes.

Definition 3.1.

A tag-based signature scheme $\mathsf {SIG_{t}}= (\mathsf {Gen_{t}},\mathsf {Sig_{t}},\mathsf {Ver_{t}})$ with message space $\mathcal {M}_k$ and tag space $\mathcal {T}_k$ consists of three PPT algorithms. The key generation algorithm $( pk , sk ) \leftarrow \mathsf {Gen_{t}}(1^k)$ takes as input a security parameter and outputs a key pair $( pk , sk )$. The signing algorithm $\sigma \leftarrow \mathsf {Sig_{t}}( sk ,M,t)$ computes a signature $\sigma$ on input a secret key $sk$, message $M$, and tag $t$. The verification algorithm $\mathsf {Ver_{t}}( pk ,M,\sigma ,t) \in \{0,1\}$ takes as input a public key $pk$, message $M$, signature $\sigma$, and a tag $t$, and outputs a bit. For correctness, we require for any $k\in {\mathbb {N}}$, all $( pk , sk ) \leftarrow \mathsf {Gen_{t}}(1^k)$, all $M\in \mathcal {M}_k$, all $t\in \mathcal {T}_k$, and all $\sigma \leftarrow \mathsf {Sig_{t}}( sk ,M,t)$ that $\mathsf {Ver_{t}}( pk ,M,\sigma ,t)=1$.

We define a mild security notion for tag-based schemes, dubbed $\text {EUF-dnaCMA}_m^*$security, which requires an adversary $F$ to initially specify all (distinct) messages $M_i$ it wants signed, along with corresponding tags $t_i$. Only then, $F$ gets to see a public key, and is subsequently expected to produce a forgery for an arbitrary fresh message $M^*$, but with respect to an already used tag $t^*\in \{t_i\}_i$. As a slightly technical (but crucial) requirement, we only allow $F$ to initially specify at most $m$messages $M_i$ with tag $t_i = t^*$. We call $m$ the tag-collision parameter; it influences key and signature sizes, and the security reduction.

Definition 3.2.

(EUF-dnaCMA $_m^*$) Let $m\in {\mathbb {N}}$. A tag-based signature scheme $\mathsf {SIG_{t}}$ is existentially unforgeable under distinct-message non-adaptive chosen-message attacks with $m$-fold tag-collisions (short: $\text {EUF-dnaCMA}_m^*$secure) iff $\mathsf {Adv}^{\mathsf {euf\text{- }dnacma^*_m}}_{\mathsf {SIG_{t}},F}(k) \,{:=}\, \Pr \left[ {\mathsf {Exp}^{\mathsf {euf\text{- }dnacma^*_m}}_{\mathsf {SIG_{t}},F}(k)=1}\right]$ is negligible for any PPT adversary $F$. Here, experiment $\mathsf {Exp}^{\mathsf {euf\text{- }dnacma^*_m}}_{\mathsf {SIG_{t}},F}(k)$ is defined in Fig. 2.

Fig. 2

$\text {EUF-dnaCMA}_m^*$experiment for tag-based signature schemes

In this section, we will show how to use a $\text {EUF-dnaCMA}_m^*$secure scheme $\mathsf {SIG_{t}}$to build an EUF-dnaCMA secure scheme $\mathsf {SIG}$. (Full EUF-CMA security can then be achieved using a chameleon hash function [23].)

To this end, we separate the tag space $\mathcal {T}_k$ into $l \,{:=}\,\lfloor \log _c(k)\rfloor$ pairwise disjoint sets $\mathcal {T}_i'$, such that $|\mathcal {T}_i'| = 2^{\lceil c^i \rceil }$. Here, $c>1$ is a granularity parameter that will affect key and signature sizes, and the security reduction. For instance, if $c=2$ and $\mathcal {T}_k = \{0,1\}^k$, then we may set $\mathcal {T}_i'\,{:=}\, \{0,1\}^{2^i}$. The constructed signature scheme $\mathsf {SIG}$assigns to each message $M$a vector of tags $(t_1,\ldots ,t_l)$, where each tag is derived from the message $M$by applying a pseudorandom function as $t_i\,{:=}\,\mathsf {PRF}^{\mathcal {T}_i'}_\kappa (M)$. The PRF seed $\kappa$ is part of $\mathsf {SIG}$’s public key.⁴

A $\mathsf {SIG}$-signature is of the form $\sigma =(\sigma _i)_{i=1}^l$, where each $\sigma _i \leftarrow \mathsf {Sig_{t}}( sk ,M,t_i)$ is a signature according to $\mathsf {SIG_{t}}$ with message $M$ and tag $t_i$. This signature is considered valid if all $\sigma _i$ are valid w.r.t. $\mathsf {SIG_{t}}$.

The crucial idea is to define the sets $\mathcal {T}_i'$ of allowed tags as sets quickly growing in $i$. This means that $(m+1)$-tag-collisions (i.e., the same tag $t_i$ being chosen for $m+1$ different signed messages) are very likely for small $i$, but become quickly less likely for larger $i$.

Concretely, let $\mathsf {SIG_{t}}=(\mathsf {Gen_{t}}, \mathsf {Sig_{t}},\mathsf {Ver_{t}})$ be a tag-based signature scheme with tag space $\mathcal {T}_k= \bigcup _{i=1}^l \mathcal {T}_i'$, let $m\in {\mathbb {N}}$ and $c>1$, and let $\mathsf {PRF}$be a PRF. $\mathsf {SIG}$is described in Fig. 3.

Fig. 3

Our EUF-dnaCMA secure signature scheme

It is straightforward to verify $\mathsf {SIG}$’s correctness. Before turning to the formal proof, we first give an intuition into why $\mathsf {SIG}$is EUF-dnaCMA secure. We will map an adversary $F$on $\mathsf {SIG}$’s EUF-dnaCMA security to an adversary $F'$ on $\mathsf {SIG_{t}}$’s $\text {EUF-dnaCMA}_m^*$security. Intuitively, $F'$ will internally simulate the EUF-dnaCMA security experiment for $F$and embed its own $\mathsf {SIG_{t}}$-instance (with public key $pk '$) in the $\mathsf {SIG}$-instance of $F$ by setting $pk \,{:=}\, ( pk ',\kappa )$. In addition, the seed $\kappa$ for $\mathsf {PRF}$is chosen internally by $F'$.

Say that $F$makes $q=q(k)$ (non-adaptive) signing requests for messages $M_1,\ldots ,M_q$. To answer these $q$ requests, $F'$ can obtain signatures under $pk '$ from its own $\text {EUF-dnaCMA}_m^*$experiment. The corresponding tags are chosen as in $\mathsf {SIG}$, as $t_i^{(j)}=\mathsf {PRF}^{\mathcal {T}_i}_\kappa (M_j)$. Once $F$produces a forgery $\sigma ^*=(\sigma ^*_i)_{i=1}^l$, $F'$ will try to use $\sigma ^*_{i^*}$ (with tag $t^*_{i^*}=\mathsf {PRF}^{\mathcal {T}_{i^*}}_\kappa (M^*)$ for some appropiate $i^* \in [l]$) as its own forgery.

Indeed, $\sigma ^*_{i^*}$ will be a valid $\mathsf {SIG_{t}}$-forgery (in the $\text {EUF-dnaCMA}_m^*$experiment) if (a) $F'$ did not initially request signatures for more than $m$messages for the forgery tag $t^*_{i^*}$; and (b) $t^*_{i^*}$ already appears in one of $F'$’s initial signature requests. Our technical handle to make this event likely will be a suitable choice of $i^*$. First, recall that the $i$-th signature $\sigma _i$ uses $\lceil c^i\rceil$-bit tags. We will hence choose $i^*$ such that

• (i) the probability of an $(m+1)$-tag-collision among the $t_{i^*}^{(j)}$ is significantly lower than $F$’s success probability (so $F$will sometimes have to forge signatures when no $(m+1)$-tag collision occurs), and

• (ii) $|\mathcal {T}_{i^*}'|=2^{\lceil c^{i^*} \rceil }$ is polynomially small (so all tags in $\mathcal {T}_{i^*}'$ can be initially queried by $F'$).

We turn to a formal proof:

Theorem 3.3.

If $\mathsf {PRF}$is a PRF and $\mathsf {SIG_{t}}$is an $\text {EUF-dnaCMA}_m^*$secure tag-based signature scheme, then $\mathsf {SIG}$is EUF-dnaCMA secure. Concretely, let $F$be an EUF-dnaCMA forger on $\mathsf {SIG}$that makes $q=q(k)$ signature queries and has advantage $\varepsilon \,{:=}\, \mathsf {Adv}^{\mathsf {euf\text{- }dnacma}}_{\mathsf {SIG}, F}(k)$ with $\varepsilon >1/p(k)$ for infinitely many $k\in {\mathbb {N}}$. Then, there exists an $\text {EUF-dnaCMA}_m^*$forger $F'$ on $\mathsf {SIG_{t}}$that makes $q'(k)\le 2\cdot \left( \frac{2\cdot q^{m+1}}{\varepsilon (k)}\right) ^{c/m}+l\cdot q$ signature queries and has advantage $\varepsilon '\,{:=}\,\mathsf {Adv}^{\mathsf {euf\text{- }dnacma^*_m}}_{\mathsf {SIG_{t}},F'}(k)$, and a PRF distinguisher with advantage $\varepsilon _{\mathsf {PRF}}$ such that

$$\begin{aligned} \varepsilon ' \ge \varepsilon /2-\varepsilon _{\mathsf {PRF}}-\frac{p''(k)}{|\mathcal {M}_k|} \end{aligned}$$

for infinitely many $k$, where $p''(k)$ is a suitable polynomial, and $\mathcal {M}_k$ denotes $\mathsf {SIG_{t}}$’s (and thus $\mathsf {SIG}$’s) the message space.

Proof

Setup and sign First, $F'$ receives messages $M_1,\dots ,M_q$ from $F$. $F'$ chooses the challenge instance $i^*$ such that the probability of an $(m+1)$-tag collision is at most $\varepsilon (k)/2$, i.e., such that

$$\begin{aligned} \Pr \left[ { \exists \text { distinct }j_0,\ldots ,j_m\in [q] \text { with } t^{(j_0)}_{i^*} = \ldots = t^{(j_m)}_{i^*} }\right] \le \frac{\varepsilon (k)}{2}, \end{aligned}$$

(1)

(where the probability is over independently chosen $t^{(j)}_{i^*}\leftarrow \mathcal {T}_{i^*}'$), and such that $|\mathcal {T}_{i^*}'|$ is polynomial in $k$.⁵ We will prove in Lemma 3.5 that

$$\begin{aligned} i^* \,{:=}\, \left\lceil \log _c\left( \log _2\left( \frac{2\cdot q^{m+1} }{\varepsilon (k)}\right) ^{1/m}\right) \right\rceil \end{aligned}$$

is an index that fulfills these conditions. $F'$ then chooses a PRF key $\kappa \leftarrow \{0,1\}^k$.

Recall that a signature $\sigma = (\sigma _{1},\ldots ,\sigma _{l})$ of $\mathsf {SIG}$ consists of $l$ signatures of $\mathsf {SIG_{t}}$. In the sequel, we write $\sigma ^{(j)} = (\sigma _1^{(j)},\ldots ,\sigma ^{(j)}_l)$ to denote the $\mathsf {SIG}$-signature for message $M_j$, for all $j \in \{1,\ldots ,q\}$. Adversary $F'$ uses its signing oracle provided from the $\mathsf {SIG_{t}}$-security experiment to simulate these $\mathsf {SIG}$-signatures. To this end, it proceeds as follows.

In order to simulate all signatures $\sigma ^{(j)}_{i}$ with $i \ne i^*$, $F'$ computes $t_i^{(j)}\,{:=}\,\mathsf {PRF}^{\mathcal {T}_i'}_\kappa (M_j)$ and defines message-tag pair $(M_j,t^{(j)}_{i})$. $F'$ will later request signatures for these $(l-1)\cdot q$ message-tag pairs from its $\text {EUF-dnaCMA}_m^*$-challenger. Note that $t_i^{(j)} \not \in \mathcal {T}_{i^*}'$ for all $i \ne i^*$, since the sets $\mathcal {T}_1',\ldots ,\mathcal {T}_l'$ are pairwise disjoint.

To compute the $i^*$-th $\mathsf {SIG_{t}}$-signature $\sigma _{i^*}^{(j)}$ contained in $\sigma ^{(j)}$, $F'$ proceeds as follows. First, it computes $t_{i^*}^{(j)}\,{:=}\,\mathsf {PRF}^{\mathcal {T}_{i^*}'}_\kappa (M_j)$ for all $j \in \{1,\ldots ,q\}$. If an $(m+1)$-fold tag-collision occurs, then $F'$ aborts. This defines $q$ more message-tag-pairs ($M_j,t_j$) for $j \in \{1,\ldots ,q\}$. Note that the list $(t_{i^*}^{(1)},\ldots ,t_{i^*}^{(q)})$ need not contain all elements of $\mathcal {T}_{i^*}'$, that is, it might hold that $\mathcal {T}_{i^*}' \setminus \{t_{i^*}^{(j)}\}_j\ne \emptyset$.

If this happens, then $F'$ chooses for each so far unused tag $t\in \mathcal {T}_{i^*}'\setminus \{t_{i^*}^{(j)}\}_j$ a different uniformly selected dummy message $M'_{t}\in \mathcal {M}_k\setminus \{M_j\}_j$. (Here, we implicitly assume that $|\mathcal {M}_k|>m(|\mathcal {T}_{i^*}'|-1)$, which guarantees that sufficiently many distinct dummy messages can be chosen.) This defines no more than $|\mathcal {T}_{i^*}'|$ further message-tag-pairs $(M,t)$ for each $t\in \mathcal {T}_{i^*}' \setminus \{t_{i^*}^{(1)},\ldots ,t_{i^*}^{(q)}\}$. We do this since $F'$ has to re-use an already queried tag for a valid forgery later, and $F'$ does not know at this point which tag $F$is going to use in his forgery later.

Finally, $F'$ requests signatures for all message-tag-pairs from its challenger, and receives in return signatures $\sigma ^{(j)}_{i^*}$ for all $j$, as well as a public key $pk '$. (The number of requested signatures is at most $|\mathcal {T}_{i^*}'|+q\cdot l$, which can be bounded as claimed using Lemma 3.5.)

$F'$ defines $pk \,{:=}\, ( pk ',\kappa )$ and hands $( pk ,\sigma ^{(1)},\ldots ,\sigma ^{(q)})$ to $F$. Note that each $\sigma ^{(j)}$ is a valid $\mathsf {SIG}$-signature for message $M_j$.

Extraction Suppose that $F$eventually forges a signature $\sigma ^*=(\sigma ^*_i)_{i=1}^l$ for a fresh message $M^* \not \in \{M_1,\ldots ,M_q\}$. If $M^*$ is a previously selected dummy message, then $F'$ aborts. Otherwise, it forwards $(M^*, \sigma ^*_{i^*},\mathsf {PRF}^{\mathcal {T}_{i^*}'}_\kappa (M^*))$ to the challenger of the $\text {EUF-dnaCMA}_m^*$security experiment.

This concludes the description of $F'$.

Analysis We now turn to $F'$’s analysis. Let $\mathsf {bad}_{\mathsf {abort}}$ be the event that $F'$ aborts. It is clear that $F'$ successfully forges a signature whenever $F$does so and $\mathsf {bad}_{\mathsf {abort}}$ does not occur. Note that the dummy messages $M'$ are independent of the view of $F$, thus $M^*$ is a dummy message with probability at most $|\mathcal {T}_{i^*}'|/(|\mathcal {M}_k|-m|\mathcal {T}_{i^*}'|)$. Furthermore, by Lemma 3.5, there is a polynomial $p'(k)$ with $m|\mathcal {T}_{i^*}'|\le p'(k)$. Hence, there is another polynomial $p''(k)$, such that the probability that $M^*$ is a dummy message is at most $p''(k)/|\mathcal {M}_k|$. Hence, to prove our theorem, it suffices to show that $\Pr \left[ {\mathsf {bad}_{\mathsf {abort}}}\right] \le \varepsilon /2+\varepsilon _{\mathsf {PRF}} + p''(k)/|\mathcal {M}_k|$, since this leaves a nonnegligible advantage for $F'$.

First, note that the probability of an $(m+1)$-tag collision would be at most $\varepsilon /2$ by (1) if the tags $t_{i^*}^{(j)}$ were chosen truly uniformly and independently from $\mathcal {T}_{i^*}'$. Now recall that the actual choice of the $t_{i^*}^{(j)}=\mathsf {PRF}^{\mathcal {T}_{i^*}'}_\kappa (M_j)$ was performed in a way that uses $\mathsf {PRF}$only in a black-box way. Hence, if $(m+1)$-tag collisions (and thus $\mathsf {bad}_{\mathsf {abort}}$) occurred significantly more often than with truly uniform tags, we had a contradiction to $\mathsf {PRF}$’s pseudorandomness. (Note that this implicitly uses that all messages $M_j$ queried by $F$are distinct and thus lead to different PRF queries.) Concretely, a PRF distinguisher that simulates $F'$ until the decision to abort is made shows $\Pr \left[ {\mathsf {bad}_{\mathsf {abort}}}\right] \le \varepsilon /2+\varepsilon _{\mathsf {PRF}}+p''(k)/|\mathcal {M}_k|$, and thus the theorem.$\square$

In order to obtain a fully EUF-CMA secure signature scheme, one may combine our EUF-dnaCMA secure scheme with a suitable chameleon hash function or a one-time signature scheme. This is a very efficient standard construction, see for instance [20, Lemma 2.3] for details.⁶ However, we will give more concrete optimized and fully secure schemes later on.

We now turn to the analysis of selecting the challenge index. For this, the following Lemma 3.4 will be helpful.

Lemma 3.4.

([18], Lemma 2.3) Let A be a set with $|A|=a$. Let $X_1,\dots ,X_q$ be $q$ independent random variables, taking uniformly random values from $A$. Then, the probability that there exist $m+1$ pairwise distinct indices $i_1,\dots ,i_{m+1}$ such that $X_{i_1}=\dots =X_{i_{m+1}}$ is upper bounded by $\frac{q^{m+1}}{a^m}$.

Lemma 3.5.

In the situation in Theorem 3.3,

$$\begin{aligned} i^* \,{:=}\, \left\lceil \log _c\left( \log _2\left( \frac{2\cdot q^{m+1} }{\varepsilon (k)}\right) ^{1/m}\right) \right\rceil \end{aligned}$$

(2)

is an index that guarantees (1) and $|\mathcal {T}_{i^*}'|\le p'(k)$ for a suitable polynomial $p'(k)$ and all $k\in {\mathbb {N}}$ with $\varepsilon (k)\ge 1/p(k)$.

Proof

From Lemma 3.4, we obtain

$$\begin{aligned} \Pr \left[ { \exists \text { distinct }j_0,\dots ,j_m\text { with } t^{(j_0)}_{i^*} = \dots = t^{(j_m)}_{i^*} }\right] \le \frac{q^{m+1}}{|\mathcal {T}_{i^*}'|^m} = \frac{q^{m+1}}{2^{m\cdot \lceil c^{i^*}\rceil }} \mathop {\le }\limits ^{(2)}\frac{q^{m+1}}{\left( \frac{2q^{m+1}}{\varepsilon (k)}\right) } =\frac{\varepsilon (k)}{2}. \end{aligned}$$

Furthermore,

$$\begin{aligned} |\mathcal {T}_{i^*}'| = 2^{\lceil c^{i^*}\rceil } \mathop {\le }\limits ^{(2)}2\cdot 2^{c\cdot \log _2((2q^{m+1}/\varepsilon (k))^{1/m})} = 2\cdot \left( \frac{2q^{m+1}}{\varepsilon (k)}\right) ^{c/m} \mathop {\le }\limits ^{\varepsilon (k)\ge 1/p(k)}2\cdot \left( 2p(k)q^{m+1}\right) ^{c/m}, \end{aligned}$$

which is bounded by a suitable polynomial $p'(k)$.

4 Our CDH-Based Scheme

In this section, we construct a fully EUF-CMA-secure signature scheme based on the CDH assumption. We start with constructing a tag-based scheme, which is derived from the stateful CDH-based scheme of Hohenberger and Waters [21], and prove it $\text {EUF-dnaCMA}_m^*$-secure. Then, we can apply our generic transformation from Sect. 3 to achieve full EUF-CMA security. Finally, we illustrate some optimizations that allow us to reduce the size of public keys and signatures, for instance, by aggregation. Our scheme is the first fully secure CDH-based signature scheme with such compact public keys.

Definition 4.1.

(CDH assumption) We say that the Computational Diffie–Hellman (CDH) assumption holds in a group $\mathbb {G}$of order $p$ iff $\mathsf {Adv}^{\mathsf {cdh}}_{\mathbb {G},F}(k) \,{:=}\, \mathrm{Pr}\big [F(1^k,g,g^a,g^b) =g^{ab}\big ]$ is negligible for any PPT adversary $F$, where $g\leftarrow \mathbb {G}$ and $a,b\leftarrow {\mathbb {Z}}_p$ are uniformly chosen.

CDH Construction The signature scheme $\mathsf {SIG}^{\mathsf {CDH}}$ described in Fig. 4 is derived from the CDH-based scheme of [21], but with two modifications. First, we substitute the implicit chameleon hash function $u^mv^r$ used in [21] with a product $\mathbf{u}^{M}=\prod _{i=0}^{m}u_i^{M^i}$. Second, we omit the $w^{\lceil \log (t)\rceil }$-factor in the “Boneh–Boyen hash function” which simplifies this part to $(z^th)^s$. From now on, we assume that $\mathbb {G}$and $\mathbb {G}_T$ are groups of prime order and $e: \mathbb {G}\times \mathbb {G}\rightarrow \mathbb {G}_T$ is an efficiently computable nondegenerate bilinear map, i.e., $e(g,g) \ne 1$ for $g \ne 1$ and $e(g^a, g^b) = e(g,g)^{ab}$ for $a,b \in {\mathbb {Z}}$. Our message space in this construction is $\mathcal {M}={\mathbb {Z}}_p$. (Technically, if $\mathbb {G}$is not fixed for a given security parameter, then a fixed message message space can be, e.g., ${\mathbb {Z}}_{2^\ell }$, where $2^\ell$ lower bounds all possible $p=|\mathbb {G}|$ for this security parameter.)

Fig. 4

The modified Hohenberger–Waters CDH-based signature scheme $\mathsf {SIG}^{\mathsf {CDH}}$ [21]

Theorem 4.2.

If the CDH assumption holds in $\mathbb {G}$, then the scheme $\mathsf {SIG}^{\mathsf {CDH}}$ from Fig. 4 is $\text {EUF-dnaCMA}_m^*$-secure. Let $F$be a PPT adversary with advantage $\varepsilon \,{:=}\,\mathsf {Adv}^{\mathsf {euf\text{- }dnacma^*_m}}_{\mathsf {SIG}^{\mathsf {CDH}}, F} (k)$ asking for $q\,{:=}\,q(k)$ signatures; then, it can be used to solve a CDH challenge with probability at least $\varepsilon /q'$, where $q'$ denotes the number of distinct tags queried by $F$.

Proof.

Public key setup The simulation receives a CDH-Challenge $(g, g^a, g^b)$ and pairs $(M_i, t_i)_{i\in [q]}$ for which the adversary $F$asks for signatures. We first guess an index ${i^*}\leftarrow [q]$ for which we suppose $F$will forge a signature on a fresh message $M^*\notin \{M_{i}\}_i$ but with $t^*=t_{{i^*}}$. The adversary $F$queries $q = \sum _{i=1}^{q'}{m_i}>0$ signatures for messages with tags where $q'$ is the number of distinct tags $(t'_i)_{i \in [q']}$ and $m_i$ the number of messages queried for tag $t'_i$. During the simulation, we define by $M^*_j, j=1,\ldots ,m_{{i^*}}$, the corresponding messages for tag $t_{{i^*}}$. Using these, we construct a polynomial $f(X)\,{:=}\,\prod _{i=1}^{m_{{i^*}}}(X-M_i^*)=\sum _{i=0}^{m_{{i^*}}} d_iX^i\in {\mathbb {Z}}_p[X]$ for some appropriate coefficients $d_0,\ldots ,d_{m_{{i^*}}}\in {\mathbb {Z}}_p$. In particular, for $m_{{i^*}}=0$ we have $\prod _{i=1}^{0}(X-M_i^*)=1$.

Next, we set up the public key for $F$by first choosing random $r_0,\ldots ,r_m, x_z, x_h\in {\mathbb {Z}}_p$ and then set $u_i\,{:=}\,(g^b)^{d_i}g^{r_i}, i=0,\ldots ,m$, where $d_i=0$ for $i>m_{{i^*}}$ , $z\,{:=}\,g^bg^{x_z}$, and $h\,{:=}\,g^{-bt_{{i^*}}}g^{x_h}$. The simulation outputs $pk \,{:=}\,(g, g^a, u_0,\ldots , u_{m}, z, h)$ and implicitly sets the secret key as $sk \,{:=}\,a$. We set $r(X)\,{:=}\,\sum _{i=0}^mr_iX^i$ so we can write $\mathbf{u}^{M}=g^{bf(M)+r(M)}$.

Signing Now, there are two cases that we have to consider when $F$asks for a signature on $(M_i, t_i)$.

If $t_i=t_{{i^*}}$ and thus $M_i=M^*_j$ for some $j=1,\ldots ,m_{{i^*}}$, then we can compute a valid signature as follows: we choose a random $s_i\leftarrow {\mathbb {Z}}_p$ and set $\sigma _{i}\,{:=}\,(\tilde{\sigma }_{1,i},\tilde{\sigma }_{2,i})$, where

$$\begin{aligned} \tilde{\sigma }_{1,i}=(g^a)^{r(M^*_j)} \cdot (z^{t_{{i^*}}}h)^{s_i},\tilde{\sigma }_{2,i}=g^{s_i}. \end{aligned}$$

We verify this by using that $f(M^*_j)=0$, i.e.,

$$\begin{aligned}\tilde{\sigma }_{1,i}=(g^a)^{r(M^*_j)}\cdot (z^{t_{{i^*}}}h)^{s_i} =(g^{bf(M^*_j)}g^{r(M^*_j)})^a\cdot (z^{t_{{i^*}}}h)^{s_i} =\big (\mathbf u ^{M^*_j}\big )^a\cdot (z^{t_{{i^*}}}h)^{s_i}. \end{aligned}$$

If $t_i\ne t_{{i^*}}$, then following the original Boneh–Boyen simulation, choose a random $s'_i\leftarrow {\mathbb {Z}}_p$ and set $S_i\,{:=}\,g^{s'_i}/(g^a)^{f(M_i)/(t_i-t_{{i^*}})}=g^{s'_i-af(M_i)/(t_i-t_{{i^*}})}$. We compute our valid signature $\sigma _i\,{:=}\,(\tilde{\sigma }_{1,i}, \tilde{\sigma }_{2,i})$ as follows:

$$\begin{aligned} \tilde{\sigma }_{1,i}=(g^a)^{r(M_i)}\cdot S_i^{x_zt_i+x_h}\cdot (g^b)^{s'_i(t_i-t_{{i^*}})},\;\tilde{\sigma }_{2,i}=S_i. \end{aligned}$$

Thus, implicitly, we set the randomness $s_i=s'_i-af(M_i)/(t_i-t_{{i^*}})$ and obtain $S_i=g^{s_i}$.

We verify this by showing that

$$\begin{aligned} \tilde{\sigma }_{1,i}&=(g^a)^{r(M_i)}\cdot S_i^{x_zt_i+x_h}\cdot (g^b)^{s'_i(t_i-t_{{i^*}})}\\&=(g^{r(M_i)})^a\cdot (g^{x_zt_i}g^{x_h})^{s_i}\cdot (g^{b})^{s'_i(t_i-t_{{i^*}})}\\&=(g^{ab})^{f(M_i)}\cdot (g^{r(M_i)})^a\cdot (g^{x_zt_i}g^{x_h})^{s_i}\cdot (g^{b})^{s'_i(t_i-t_{{i^*}})}\cdot (g^{-ab})^{f(M_i)}\\&=\big (g^{bf({M_i})+r(M_i)})^a\cdot \big (g^{x_zt_i}g^{x_h})^{s_i}\cdot \big (g^{b(t_i-t_{{i^*}})}\big )^{s_i}\\&=\big (\mathbf{u}^{M_i}\big )^a\cdot (g^{b+x_z})^{t_i}\cdot (g^{-bt_{{i^*}}+x_h}\big )^{s_i}\\&=\big (\mathbf{u}^{M_i}\big )^a\cdot (z^{t_i}h)^{s_i}. \end{aligned}$$

Extract from forgery The adversary $F$responds with $(M^*, \sigma ^*, t^*)$ for some tag $t^*\in \{t_1, \dots , t_{q'}\}$ and $\sigma ^* = (\tilde{\sigma }_1^*,\tilde{\sigma }_2^*)$. We abort if $\sigma ^*$ is not a valid forgery. Otherwise, since the verification equation holds, we have

$$\begin{aligned} \tilde{\sigma }_1^*=(\mathbf u ^{M^*})^a(z^{t^*} h)^{s^*},\;\tilde{\sigma }_2^*=g^{s^*}. \end{aligned}$$

If $t_{{i^*}}\ne t^*$, then we abort; otherwise, our guess was correct, and it holds that

$$\begin{aligned} \tilde{\sigma }_1^*&=\left( g^b\right) ^{f(M^*)}\left( g^{r(M^*)}\right) ^a\left( (g^{b+x_z})^{t^*}(g^{-bt_{{i^*}}+x_h})\right) ^{s^*}\\&=g^{abf(M^*)}g^{ar(M^*)}\left( g^{x_zt^*}g^{x_h}\right) ^{s^*}\\&=g^{abf(M^*)}g^{ar(M^*)}g^{s^*(x_zt^*+x_h)}. \end{aligned}$$

Since $M^*\ne M_j^*$, we have $f(M^*)\ne 0$, and the simulator can compute

$$\begin{aligned} \left( \tilde{\sigma }_1^*/\big (g^{ar(M^*)} \tilde{\sigma }_2^{*^{(x_zt^*+x_h)}}\big )\right) ^{1/f(M^*)}=g^{ab}. \end{aligned}$$

Analysis We show that the adversary $F$cannot distinguish effectively between the experiment and the simulation. We denote by $\varepsilon$ the advantage of the adversary $F$ in the experiment, and by $\mathsf {success}$ the event that the simulation outputs a solution $g^{ab}$. The simulator does not pick $(u_i)_{i = 0}^m$, $z$, and $h$ at random, but sets them as described above. Since the $r_i$, $x_z$ and $x_h$ are randomly chosen, this yields the correct distribution, and so the view of the adversary is still the same as in the experiment. The simulator is successful if it does not abort, which means, if it guesses $t^*$ correctly and if $F$is also successful. Hence, we have $\Pr \left[ {\mathsf {success}}\right] =\frac{\varepsilon }{q'}$.$\square$

4.1 Optimizations

Now, with this result and our generic transformation from Sect. 3, we can construct a stateless signature scheme, which is proven EUF-dnaCMA secure by Theorem 3.3. Then, we add an explicit chameleon hash function $\mathsf {CH}_{(g,w)}(M,r)\,{:=}\,g^Mw^r$ in each instance $i=1,\dots ,\lfloor \log _c(k)\rfloor$ to achieve a fully EUF-CMA-secure signature scheme. This signature scheme does have a constant size public key, but signatures consist of $\mathbf {O}(\log k)$ group elements, i.e., $\sigma =(\sigma _1,\dots ,\sigma _{\log k})$ where $\sigma _i=(\tilde{\sigma }_{1,i}, \tilde{\sigma }_{2,i},r_i)$.

Now, we concentrate on how we can improve this and achieve constant size signatures. This will be done by aggregation, essentially by multiplying the signatures of each instance similar to [25]. We re-use $u_0,\dots ,u_{m}$, one $sk \,{:=}\,a$ and one randomness $s$ for all instances $i$ (see Fig. 5). Unfortunately, we need additional elements in the public key for the aggregation to work. In this sense, our optimization is rather a tradeoff: we prefer constant-size signatures with public keys of logarithmic length over logarithmic-length signatures with constant-size public keys.

Fig. 5

The optimized CDH-based signature scheme $\mathsf {SIG}_{\mathsf {opt}}^{\mathsf {CDH}}$

Theorem 4.3.

If the CDH assumption holds in $\mathbb {G}$, then the optimized CDH-based signature scheme in Fig. 5 is an EUF-CMA secure signature scheme. Let $F$be a PPT adversary with advantage $\varepsilon \,{:=}\,\mathsf {Adv}^{\mathsf {euf\text{- }cma}}_{\mathsf {SIG}_{\mathsf {opt}}^{\mathsf {CDH}}, F}(k)$ asking for $q\,{:=}\,q(k)$ signatures, then it can be used to solve a CDH challenge with probability at least

$$\begin{aligned} \frac{\varepsilon ^{c/m+1}-2\varepsilon ^{c/m} (\varepsilon _{\mathsf {PRF}}+\varepsilon _{\mathsf {CH}})}{2^{2+c/m}\cdot q^{c+c/m}}, \end{aligned}$$

where $\varepsilon _{\mathsf {PRF}}$ and $\varepsilon _{\mathsf {CH}}$ correspond to the advantages for breaking $\mathsf {PRF}$and $\mathsf {CH}$, respectively.

Proof.

We only sketch the proof here, because it is essentially a combination of the proofs from Theorems 4.2 and 3.3. We emphasize the differences and important parts. We have to deal with $l=\lfloor \log _c(k)\rfloor$ instances and obtain our signature by generic aggregation.

Public key setup First, we select an index ${i^*}$ and guess a tag $t_{{i^*}}$ from the corresponding set $\mathcal {T}_{{i^*}}$. Next, we pick a random $\kappa \leftarrow \left\{ 0,1\right\} ^k$ and random distinct $M_1, \dots , M_q, r_1, \dots , r_q\leftarrow {\mathbb {Z}}_p$ and compute $x_j=\mathsf {CH}(M_j,r_j), j\in [q]$.⁷ Due to the collision resistance of our chameleon hash function and the fact that $|{\mathbb {Z}}_p|>q$, we can assume that all $x_j$ are distinct; otherwise, we abort. From that, we derive a tag $t_{i}^{(j)}\,{:=}\,\mathsf {PRF}_{\kappa }^{ \mathcal {T}_i}(x_j)$ for each instance $i\in [l]$. Then, we consider the set $J=\{\,j\in [q]\,|t_{{i^*}}^{(j)}=t_{{i^*}}\}$. If $|J|>m$, we abort; otherwise, $|J|=m'\le m$. With that, we can, similar to Theorem 4.2, compute a polynomial $f$ s.t. $f(x_j)=0$ for $j\in J$. We set up $u_0, \dots , u_{m'}, h, z_{{i^*}}$ as before in Theorem 4.2 to embed our challenge here and choose random $z_i$ for $i\in [q]\setminus \{{i^*}\}$ by choosing random exponents $x_{z_i}$ for them.

Signing The adversary will send us messages $M_1,\dots ,M_q$, and we have to compute a valid signature $\sigma ^{(j)}=(\tilde{\sigma }_{1,j}, \tilde{\sigma }_{2,j}, r_j')$ for each of them. We compute $r_j'$ s.t. $x_j=\mathsf {CH}(M_j,r_j')$. Thus, $t_i^{(j)}$ belongs to $M_j$, for $i=1,\dots ,l$. Now, we consider the instance $i={i^*}$:

Again, we have two cases, either $t_{{i^*}}^{(j)}=t_{{i^*}}$ or $t_{{i^*}}^{(j)}\ne t_{{i^*}}$. In both cases, we can apply the same techniques as in Theorem 4.2 to obtain a valid $(\mathbf{u}^{x_j})^a\big (z_{{i^*}}^{t_{{i^*}}^{(j)}}h\big )^{s_j}$.

For the other instances $i\ne {i^*}$, we can compute $\big (z_i^{t_{i}^{(j)}}\big )^{s_j}=\big (g^{x_{z_i}t_{i}^{(j)}}\big )^{s_j}=(g^{s_j})^{x_{z_i}t_{i}^{(j)}}$ because we know the exponents $x_{z_i}$ and then can aggregate them to get

$$\begin{aligned} \sigma _j\,{:=}\,\big (\big (\mathbf{u}^{x_j})^a\big (h\prod \limits _{i=1}^{l}{z}_i^{t_{i}^{(j)}}\big )^{s_j}, g^{s_j}, r_j'\big ). \end{aligned}$$

Extract from forgery The adversary $F$responds with $(M^*, \sigma ^*)$ where $\sigma ^* = (\tilde{\sigma }_1^*,\tilde{\sigma }_2^*, r^*)$ and $M^*\ne M_j$ for $j\in [q]$. Abort if $\sigma ^*$ is not valid. We can assume that $F$has not produced a collision $x^*=\mathsf {CH}(M^*,r^*)=x_j$ for some $j\in [q]$ due to the collision resistance of our chameleon hash function. Thus, we have $f(x^*)\ne 0$. Now, we compute $t^*_i=\mathsf {PRF}_\kappa ^{\mathcal {T}_i}(x^*)$ for each instance $i\in [l]$. If $t^*_{{i^*}}\ne t_{{i^*}}$, then we abort; otherwise, it holds

$$\begin{aligned} \tilde{\sigma }_1^*=(\mathbf{u}^{x^*})^a\left( h\prod \limits _{i=1}^{l}z_i^{t^*_i}\right) ^{s^*},\tilde{\sigma }^*_2=g^{s^*}. \end{aligned}$$

We can compute $(g^{s^*})^{x_{z_i}t^*_i}=\left( z_i^{t^*_i}\right) ^{s^*}$ for $i\ne {i^*}$ and obtain

$$\begin{aligned} \sigma ^*_1/\prod \limits _{i=1,i\ne {i^*}}^{l}\left( z_i^{t^*_i}\right) ^{s^*}=(\mathbf{u}^{x^*})^a\left( z_{{i^*}}^{t^*_{{i^*}}}h\right) ^{s^*}. \end{aligned}$$

Therefore, we apply the same method as in Theorem 4.2 since $f(x^*)\ne 0$ and $t^*_{{i^*}}=t_{{i^*}}$ to extract a solution $g^{ab}$.

Analysis The analysis is similar to Theorems 3.3 and 4.2. Hence,

$$\begin{aligned} \Pr [{\mathsf {success}}] \ge \frac{1}{|\mathcal {T}_{i^*}|}\left( \frac{\varepsilon }{2}-\left( \varepsilon _{\mathsf {PRF}}+\varepsilon _{\mathsf {CH}}\right) \right) \mathop {\ge }\limits ^{(*)}\frac{\varepsilon ^{1+c/m}-2\varepsilon ^{c/m}(\varepsilon _{\mathsf {PRF}}+\varepsilon _{\mathsf {CH}})}{2^{2+c/m}\cdot q^{c+c/m}}, \end{aligned}$$

where (*) holds by Lemma 3.5, since we have $|\mathcal {T}_{i^*}| \le 2\cdot \left( \frac{2q^{m+1}}{\varepsilon (k)}\right) ^{c/m}$. Here, $\varepsilon _{\mathsf {PRF}}$ is the advantage for a suitable adversary on $\mathsf {PRF}$, and $\varepsilon _{\mathsf {CH}}$ is the advantage to produce a collision for $\mathsf {CH}$, both negligible in the security parameter.$\square$

5 Our RSA-Based Scheme

In this section, we construct a stateless signature scheme $\mathsf {SIG}_{\mathsf {opt}}^{\mathsf {RSA}}$secure under the RSA assumption. The result is the most efficient RSA-based scheme currently known.

The prototype for our construction is the stateful RSA-based scheme of Hohenberger and Waters [21] which we reference as $\mathsf {SIG}_{\mathsf {HW09}}^{\mathsf {RSA}}$from now on. We first show that a stripped-to-the-basics variation of their scheme (which is tag-based but stateless), denoted $\mathsf {SIG}^{\mathsf {RSA}}$, is mildly secure, i.e., $\text {EUF-dnaCMA}_m^*$-secure. Subsequently, we apply our generic transformation from Sect. 3 and add a chameleon hash to construct a fully secure stateless scheme. Finally, we apply common aggregation techniques which yield the optimized scheme $\mathsf {SIG}_{\mathsf {opt}}^{\mathsf {RSA}}$.

5.1 Preliminaries

RSA(k) is a polynomially bounded function that maps a given security parameter $k$ to the bitlength of the RSA modulus.

Definition 5.1.

(RSA assumption) Let $N\in {\mathbb {N}}$ be the product of two distinct safe primes $P$ and $Q$ with $2^\frac{\text {RSA}(k)}{2} \le P, Q \le 2^{\frac{\text {RSA}(k)}{2} + 1} - 1$. Let $e$ be a randomly chosen positive integer less than and relatively prime to $\varphi (N) = (P - 1) (Q - 1)$. For $y \leftarrow {\mathbb {Z}}_N^\times$, we call the triple $(N, e, y)$ RSA challenge. The RSA assumption holds if for every PPT algorithm $A$the probability

$$\begin{aligned} \Pr \left[ {A(N, e, y) = x \wedge x^e \equiv y\ (mod\ N)}\right] \end{aligned}$$

is negligible in $k$ for a uniformly chosen RSA challenge $(N, e, y)$.

Lemma 5.2.

(Shamir’s trick [10, 31]) Given $w, y \in {\mathbb {Z}}_N$ together with $a,b \in {\mathbb {Z}}$ such that $w^a = y^b$ and $\gcd (a, b) = 1$, there is an efficient algorithm for computing $x \in {\mathbb {Z}}_N$ such that $x^a = y$.

Lemma 5.3.

Let $\pi (n)$ denote the number of primes $p \le n$. For $n \in {\mathbb {N}}, n \ge 2^{21}$ we have

$$\begin{aligned} \frac{n}{\log _2(n)} \le \pi (n) \le \frac{2 n}{\log _2(n)} \end{aligned}$$

Proof.

This lemma is just a variation of the well-known prime bound $\frac{n}{\ln (n) + 2} \le \pi (n) \le \frac{n}{\ln (n) - 4}$ for $n \ge 55$ [29]. We find

• $\frac{n}{\log _2(n)} \le \frac{n}{\ln (n) + 2}$ since $\log _2(n) \ge \ln (n) + 2$ for $n \ge 92 \ge e^{2 / (\log _2(e) - 1)}$ and

• $\frac{n}{\ln (n) - 4} \le \frac{2 n}{\log _2(n)}$ since $\ln (n) - 4 \ge \frac{1}{2} \log _2(n)$ for $n \ge 2^{21} \ge e^{8 / (2 - \log _2(e))}$

which proves the claim.$\square$

Lemma 5.4.

For $k \in {\mathbb {N}}$, we define $\mathbb {P}_k^*\,{:=}\, \{p \text { prime } | 2^\frac{k}{2} \le p \le 2^k \}$. It holds $|\mathbb {P}_k^*| > \frac{2^k}{5k}$.

Proof

$$\begin{aligned} |\mathbb {P}_k^*|&= \pi (2^k) - \pi (2^\frac{k}{2}) \ge \pi (2^k) - \pi (2^{\lfloor \frac{k}{2}\rfloor }) = \sum _{i = 1}^{\lceil k/2\rceil } \big (\pi \big (2^{i + \lfloor \frac{k}{2}\rfloor }\big ) - \pi \big (2^{i + \lfloor \frac{k}{2}\rfloor - 1}\big )\big ) \\&\mathop {>}\limits ^{*} \sum _{i = 1}^{\lceil k/2\rceil } \frac{2^{i + \lfloor \frac{k}{2}\rfloor - 1}}{3 \ln (2)(i + \lfloor \frac{k}{2}\rfloor )} = \frac{1}{6 \ln (2)} \sum _{i = 1}^{\lceil k/2\rceil } \frac{2^{i +\lfloor \frac{k}{2}\rfloor }}{i + \lfloor \frac{k}{2}\rfloor } > \frac{1}{6 \ln (2)} \frac{2^k}{k} > \frac{2^k}{5k} \end{aligned}$$

(*) by [32], Theorem 5.8 (Betrand’s postulate): $\pi (2^l) - \pi (2^{l - 1}) \ge \frac{2^{l - 1}}{3 \ln (2) l}$

Lemma 5.5.

For $\ell ,k \in {\mathbb {N}}$ we have that for all sets $\mathcal {X} \subseteq [2^k]$ with $|\mathcal {X}| \le 2^\ell$

$$\begin{aligned} \Pr \left[ {p \leftarrow \mathbb {P}_k^*: \exists x \in \mathcal {X} \text { such that } p | x}\right] \le \frac{10 k}{2^{k - \ell }} \end{aligned}$$

where $\mathbb {P}_k^*$is the set of primes $p$ with $2^\frac{k}{2} \le p \le 2^k$.

Proof.

For any $x \in [2^k]$, we have $|\{p \in \mathbb {P}_k^*: p | x\}| \le 2$ since the product of any three elements of $\mathbb {P}_k^*$is bigger than $2^k$. Hence,

$$\begin{aligned} \Pr \left[ {p \leftarrow \mathbb {P}_k^*: \exists x \in \mathcal {X} \text { such that } p | x}\right] \mathop {\le }\limits ^{(1)} \frac{2 |\mathcal {X}|}{|\mathbb {P}_k^*|} \mathop {\le }\limits ^{(2)} \frac{2 \cdot 2^l}{|\mathbb {P}_k^*|} \mathop {\le }\limits ^{(3)} \frac{2 \cdot 2^\ell }{\frac{2^k}{5k}} = \frac{10 k}{2^{k - \ell }} \end{aligned}$$

(1) by the union bound, (2) by assumption $|\mathcal {X}| \le 2^\ell$, (3) by Lemma 5.4.

5.2 $\text {EUF-dnaCMA}_m^*$-Secure Signature Scheme

The basic scheme $\mathsf {SIG}^{\mathsf {RSA}}$Let $N= P Q$ be an RSA modulus consistent with the RSA assumption (Definition 5.1). Basically, a $\mathsf {SIG}^{\mathsf {RSA}}$signature for a message-tag-pair $(M, t)$ is a tuple $((\mathbf{u}^{M})^\frac{1}{p} \,\,\hbox {mod}\,\,N, t)$ where $p$ is a prime derived from the tag $t$. Analogously to our CDH scheme (Sect. 4), we define $\mathbf{u}^{M}\,{:=}\, \prod _{i = 0}^mu_i^{M^i}$ using quadratic residues $(u_i)_{i = 0}^m$ to allow for the signing of up to $m$ messages with the same tag. The message space is $\{0,1\}^\ell$ where we pick $\ell = k/\max (2,m)$ for our realization—we will need later that $\frac{1}{2^{k - \ell }}$ is negligible and that $\ell m\le k$. To construct a mapping from tags to primes, we use a technique from [20] and [18]: For a PRF $\mathsf {PRF}^{\{0,1\}^{\text {RSA}(k)}}$, a corresponding key $\kappa \leftarrow \{0,1\}^k$, and a random bitstring $b \leftarrow \{0, 1\}^{\text {RSA}(k)}$, we define

$$\begin{aligned} \mathsf {P}_{(\kappa ,b)}(t) \,{:=}\, \mathsf {PRF}^{\{0,1\}^{\text {RSA}(k)}}_\kappa (t||\mu _t) \oplus b, \end{aligned}$$

where $\mu _{t} \,{:=}\, \min \{\mu \in {\mathbb {N}}: \mathsf {PRF}^{\{0,1\}^{\text {RSA}(k)}}_\kappa (t||\mu ) \oplus b \text { is prime}\}$ and $||$ denotes the concatenation of bitstrings.⁸ We call $\mu _{t}$ the resolving index of $t$. The complete scheme $\mathsf {SIG}^{\mathsf {RSA}}$is depicted in Fig. 6.

Fig. 6

The tag-based RSA scheme $\mathsf {SIG}^{\mathsf {RSA}}$

Differences to $\mathsf {SIG}_{\mathsf {HW09}}^{\mathsf {RSA}}$For readers acquainted with the stateful Hohenberger–Waters construction [21], also known as HW09a, we give a quick overview on how $\mathsf {SIG}^{\mathsf {RSA}}$relates to its prototype $\mathsf {SIG}_{\mathsf {HW09}}^{\mathsf {RSA}}$. To have the least amount of overhead, we first removed all components from $\mathsf {SIG}_{\mathsf {HW09}}^{\mathsf {RSA}}$that are not required to prove the scheme $\text {EUF-dnaCMA}_m^*$secure. This includes the chameleon hash (we are in a nonadaptive setting) and logarithm-of-tag-construction in the exponent (we guess from a small set of tags only). Our setup of $\mathsf {P}_{(\kappa ,b)}$slightly differs from the one in $\mathsf {SIG}_{\mathsf {HW09}}^{\mathsf {RSA}}$since we do need that every tag is mapped to a prime.

5.3 $\text {EUF-dnaCMA}_m^*$Security

Theorem 5.6.

If $F$is a PPT $\text {EUF-dnaCMA}_m^*$-adversary for $\mathsf {SIG}^{\mathsf {RSA}}$with advantage $\varepsilon \,{:=}\,$ $\mathsf {Adv}^{\mathsf {euf\text{- }dnacma^*_m}}_{\mathsf {SIG}^{\mathsf {RSA}}, F}(k)$ asking for $q \,{:=}\, q(k)$ signatures, then it can be used to efficiently solve an RSA challenge according to Definition 5.1 with probability at least

$$\begin{aligned} \frac{1}{\text {RSA}(k)^2}\left( \frac{\varepsilon }{8 q' \text {RSA}(k)}-\varepsilon _\mathsf {PRF}-\frac{1}{2^{\text {RSA}(k)}}\right) - {\varepsilon _\mathsf {PRF}}'-\frac{q'\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}}-\frac{10 k}{2^{k/2}} \end{aligned}$$

where $q'$ denotes the number of distinct tags queried by $F$, and $\varepsilon _\mathsf {PRF}$ and ${\varepsilon _\mathsf {PRF}}'$ are the advantage of suitable distinguishers for the PRF.

Proof.

We first describe the simulation and subsequently provide a detailed analysis. In the following $(N, e^*, y)$ denotes the RSA challenge given to the simulator. First, we guess an index ${i^*}\leftarrow [q]$ for which we suppose $F$will forge a signature on a new message $M^*\ne M_{{i^*}}$, but with $t^*=t_{{i^*}}$. The adversary $F$queries $q = \sum _{i=1}^{q'}{m_i}>0$ signatures for messages with tags where $q'$ is the number of distinct tags $(t_i)_{i \in [q']}$ and $m_i$ the number of messages queried for tag $t_i$. $(M^*_i)_{i \in [m_{i^*}]}$ denotes the list of messages queried for tag $t_{{i^*}}$.

If $e^*$is not a prime with $\log _2(e^*) \ge \frac{\text {RSA}(k)}{2}$, we abort. Otherwise, we proceed as follows:

Public key setup We guess an index ${i^*}\leftarrow [q']$ and write $t_{{i^*}}$ for the corresponding tag. Intuitively, $t_{{i^*}}$ is the tag that we will use to embed our challenge. We pick $\kappa$ and $\mu _t^*\leftarrow [\text {RSA}(k)^2]$ at random and compute $b \,{:=}\, \mathsf {PRF}^{\{0,1\}^{\text {RSA}(k)}}_\kappa (t_{{i^*}}||\mu _t^*) \oplus e^*$. If $\mathsf {P}_{(\kappa ,b)}(t_{{i^*}}) \not = e^*$ or if $\mathsf {P}_{(\kappa ,b)}(t_i) = e^*$ for any $t_i \not = t_{{i^*}}$ ($i \in [q']$), we abort. We compute $p_i \,{:=}\, \mathsf {P}_{(\kappa ,b)}(t_i)$ for $i \in [q']$ and set ${p^*}\,{:=}\, p_{{i^*}}$ (note that ${p^*}= e^*$). Next, we define two polynomials over ${\mathbb {Z}}[X]$. The first one, $f(X) \,{:=}\, \prod _{i = 1}^{m_{i^*}} (X - M^*_i)$, is determined by the messages queried for the challenge tag $t_{{i^*}}$. We have $f(X) = \sum _{i = 0}^{m_{i^*}} \alpha _i X^i$ for some appropriate coefficients $\alpha _i \in {\mathbb {Z}}$ and set $\alpha _i \,{:=}\, 0$ for $i \in \{m_{i^*}+ 1,\dots , m\}$. For the second one, we pick $\beta _i \leftarrow {\mathbb {Z}}_{N/4}$ for $i \in \{0, \dots , m\}$ and set $g(X) \,{:=}\, \sum _{i = 0}^m\beta _i X^i$. For a more comprehensive notation, we define $\phi _I \,{:=}\, \prod _{i \in ([q'] \setminus I)} p_i$ for any set of indexes $I \subseteq [q']$, $\phi \,{:=}\, \phi _\emptyset$ and $\mathbf{u}^{M}\,{:=}\, \prod _{i=0}^{m}u_i^{M^i}$. We set

$$\begin{aligned} u_i \,{:=}\, (y^{\phi _{\{{i^*}\}}\alpha _i + \phi \beta _i})^2. \end{aligned}$$

Note that for any message $M$

$$\begin{aligned} \mathbf{u}^{M}= (y^{\phi _{\{{i^*}\}}f(M) + \phi g(M)})^2. \end{aligned}$$

We send the public key $(N, (u_i)_{i = 0}^m, \kappa , b)$ to the adversary.

Signing For each query $(M, t)$, we compute the corresponding signature $\sigma$ as follows. If $t= t_{{i^*}}$, $\sigma$ is $(\hat{\sigma }, t)$ where

$$\begin{aligned} \hat{\sigma } \,{:=}\, \left( y^{\phi _{\{{i^*}\}}g(M)}\right) ^2. \end{aligned}$$

We use the fact that $M= M^*_i$ for some $i \in [m]$ and hence $f(M) = 0$ to verify

$$\begin{aligned} \left( \mathbf{u}^{M}\right) ^\frac{1}{{p^*}} \equiv ((y^{\phi _{\{{i^*}\}}f(M) + \phi g(M)})^2)^\frac{1}{{p^*}} \equiv (y^{\phi _{\{{i^*}\}} g(M)})^2 \equiv \hat{\sigma }. \end{aligned}$$

If $t= t_i \not = t_{{i^*}}$ ($i \in [q']$), the corresponding signature $\sigma$ is $(\hat{\sigma }, t)$ where

$$\begin{aligned} \hat{\sigma } \,{:=}\, \left( y^{\phi _{\{i, {i^*}\}}f(M) + \phi _{\{i\}}g(M)}\right) ^2. \end{aligned}$$

We verify

$$\begin{aligned} \left( \mathbf{u}^{M}\right) ^\frac{1}{p_i} \equiv ((y^{\phi _{\{{i^*}\}}f(M) + \phi g(M)})^2)^\frac{1}{p_i} \equiv \left( y^{\phi _{\{i,{i^*}\}}f(M) + \phi _{\{i\}} g(M)}\right) ^2 \equiv \hat{\sigma }. \end{aligned}$$

Finally, we send all signatures to the adversary.

Extract from forgery The adversary responds with $(M^*, \sigma ^*)$ where $\sigma ^* = (\hat{\sigma }, t^*)$ for some tag $t^*\in \{t_1, \dots , t_{q'}\}$. Here, if $t^*\ne t_{i^*}$ and if $\sigma ^*$ is not a valid forgery, we abort. Otherwise, since the verification equation holds, we have

$$\begin{aligned} (\sigma ^*)^{p^*}\equiv {\mathbf{u}^{M}}^* \equiv \big (y^{\phi _{\{{i^*}\}}f(M^*) + \phi g(M^*)}\big )^2 \equiv y^{2 \phi _{\{{i^*}\}}f(M^*)} y^{2 \phi g(M^*)} \end{aligned}$$

and hence

$$\begin{aligned} \big (\sigma ^* / y^{2 \phi _{\{{i^*}\}} g(M^*)}\big )^{p^*}\equiv y^{2 \phi _{\{{i^*}\}}f(M^*\big )}. \end{aligned}$$

Note that $f(M^*) \not = 0$ since $M^* \not = M^*_i$ for $i \in [m]$. Clearly, ${p^*}$ does not divide $2 \phi _{\{{i^*}\}}$. If $\gcd ({p^*}, f(M^*)) \not = 1$, then we abort. Otherwise, we use Shamir’s trick (Lemma 5.2) to compute $x$ such that $x^{p^*}\equiv y\ (mod\ N)$. Since ${p^*}= e^*$ by construction, $x$ is the output of the simulator and a solution to the RSA challenge $(N, e^*, y)$ was given.

Analysis We show that the adversary $F$cannot distinguish effectively between the experiment and the simulation. Let $X_i$ denote the event that the adversary is successful in Game $i$.

Game 0   In Game 0, the simulator runs the original $\text {EUF-dnaCMA}_m^*$experiment, and hence, we have $\Pr \left[ {X_0}\right] = \varepsilon$.

Game 1   In Game 1, the simulator aborts if $e^*$is not a prime with $\log _2(e^*) \ge \frac{\text {RSA}(k)}{2}$. Hence, we do not abort with probability

$$\begin{aligned} \frac{\pi (\varphi (N)) - \pi (2^{\text {RSA}(k)/ 2}) - 2}{\varphi (\varphi (N))} \mathop {\ge }\limits ^{(*)} \frac{1}{8 \text {RSA}(k)} \end{aligned}$$

$(*)$ since $2^{\text {RSA}(k)} \ge \varphi (\varphi (N))$, $\varphi (N) \ge N/4$, and Lemma 5.3 (all for sufficiently large $N$). Thus,

$$\begin{aligned} \Pr \left[ {X_1}\right] \ge \frac{1}{8 \text {RSA}(k)} \Pr \left[ {X_0}\right] . \end{aligned}$$

Game 2    In Game 2, the simulator aborts if $t^*\ne t_{i^*}$, for challenge tag $t^*$ and guessed tag $t_{i^*}$. In particular, for given (distinct) tags $(t_i)_{i\in [q']}$, the simulator first chooses an index $i^*\leftarrow [q']$ as above. Now, if $F$outputs a forgery $(M^*,\hat{\sigma }, t^*)$ with tag $t^*\ne t_{i^*}$, the simulator aborts. Thus, we have

$$\begin{aligned} \Pr \left[ {X_{2}}\right] \ge \frac{\Pr \left[ {X_{1}}\right] }{q'}. \end{aligned}$$

Game 3    In Game 3, we set up $\mathsf {P}_{(\kappa ,b)}$ as described in the simulation above. Concretely, we choose $\mu _t^*\leftarrow [\text {RSA}(k)^2]$ and set $b \,{:=}\, \mathsf {PRF}^{\{0,1\}^{\text {RSA}(k)}}_\kappa (t_{{i^*}}||\mu _t^*) \oplus e^*$. If $\mu _t^*$ is not the resolving index of $\mathsf {P}_{(\kappa ,b)}(t_{{i^*}})$, then we abort. We denote this event as $\mathsf {abort}_{\mathsf {\mu }}$. Assume $\mathsf {PRF}_\kappa ^{\{0,1\}^{\text {RSA}(k)}}$ is a truly random function. Now, by evaluating $\mathsf {P}_{(\kappa ,b)}$, we derive uniformly random $\text {RSA}(k)$-bit strings. By Lemma 5.3, the probability that the output of $\mathsf {P}_{(\kappa ,b)}$ is a $\text {RSA}(k)$-bit prime is at least $1/\text {RSA}(k)$. Further, for $\text {RSA}(k)^2$ $\mathsf {P}_{(\kappa ,b)}$-evaluations, the probability of not outputting a $\text {RSA}(k)$-bit prime is at most $(1-1/\text {RSA}(k))^{\text {RSA}(k)^2}$. Hence, we can construct a PRF distinguisher with probability ${\varepsilon _\mathsf {PRF}}\ge \Pr \left[ {\mathsf {abort}_{\mathsf {\mu }}}\right] -(1-1/\text {RSA}(k))^{\text {RSA}(k)^2}$. (For a detailed analysis of this Game, see [19], Proof of Theorem 4.1, Games 8–10. In particular, we have $(1-1/\text {RSA}(k))^{\text {RSA}(k)^2}\le 1/{\text {RSA}(k)^k}$.) We conclude

$$\begin{aligned} \Pr \left[ {X_3}\right] \ge \frac{1}{\text {RSA}(k)^2}\left( \Pr \left[ {X_2}\right] - \varepsilon _\mathsf {PRF}- \frac{1}{2^{\text {RSA}(k)}}\right) . \end{aligned}$$

Game 4    Now, in Game 4, we abort if $\mathsf {P}_{(\kappa ,b)}(t_i) = e^*$ for some $t_i \not = t_{{i^*}}$ ($i \in [q']$). Let $\mathsf {abort}_{\mathsf {coll}}$ denote the corresponding event. If $\mathsf {PRF}$is a truly random function, then the output of $\mathsf {P}_{(\kappa ,b)}(t_i)$ is a uniform $\text {RSA}(k)$-bit prime. By Lemma 5.3, there are at least $\frac{2^{\text {RSA}(k)}}{\text {RSA}(k)}$ such primes. Hence, the probability of a collision with $e^*$is at most $\left( \frac{q'\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}}\right)$. Using this, we can construct an adversary that distinguishes $\mathsf {PRF}$from a truly random function with advantage ${\varepsilon _\mathsf {PRF}}'\ge \Pr \left[ {\mathsf {abort}_{\mathsf {coll}}}\right] -\left( \frac{q'\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}}\right)$. Thus, it follows that

$$\begin{aligned} \Pr \left[ {X_4}\right] \ge \Pr \left[ {X_3}\right] -{\varepsilon _\mathsf {PRF}}'-\frac{q'\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}}. \end{aligned}$$

Game 5    In Game 5, we do not pick $(u_i)_{i = 0}^m$ at random but set them as described above. Since the $\beta _i$ are randomly chosen and blind the $\alpha _i$ known to the adversary, this yields a correct distribution. Hence, we have

$$\begin{aligned} \Pr \left[ {X_5}\right] = \Pr \left[ {X_4}\right] . \end{aligned}$$

The view of the adversary in this Game is exactly the view in the simulation described above.

Game 6    In Game 6, let $\mathsf {abort}_{\mathsf {gcd}}$ denote the event that $\gcd ({p^*}, f(M^*))\ne 1$. Remember that messages are bitstrings of length $\ell$. The range of $f$ is a set $\mathcal {X} \subseteq [2^k]$ containing $2^\ell$ elements at most. Therefore, by Lemma 5.5 with $\ell = k/\max (2,m)$, we have

$$\begin{aligned} \Pr \left[ {\mathsf {abort}_{\mathsf {gcd}}}\right] \le \frac{10 k}{2^{k - \ell }} = \frac{10 k}{2^{k \cdot {\frac{\max (2,m) - 1}{\max (2,m)}}}} \le \frac{10 k}{2^{k/2}} \end{aligned}$$

and, thus,

$$\begin{aligned} \Pr \left[ {X_6}\right] \ge \Pr \left[ {X_5}\right] -\frac{10 k}{2^{k/2}}. \end{aligned}$$

Finally, we summarize and see that the simulator is successful with probability at least

$$\begin{aligned}&\Pr \left[ {X_5}\right] -\frac{10 k}{2^{k/2}}\\&\quad =\Pr \left[ {X_4}\right] -\frac{10 k}{2^{k/2}}\\&\quad \ge \Pr \left[ {X_3}\right] -{\varepsilon _\mathsf {PRF}}'-\frac{q'\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}}-\frac{10 k}{2^{k/2}}\\&\quad \ge \frac{1}{\text {RSA}(k)^2}\left( \Pr \left[ {X_2}\right] -\varepsilon _\mathsf {PRF}-\frac{1}{2^{\text {RSA}(k)}}\right) -{\varepsilon _\mathsf {PRF}}'-\frac{q'\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}}-\frac{10 k}{2^{k/2}}\\&\quad \ge \frac{1}{\text {RSA}(k)^2}\left( \frac{\Pr \left[ {X_1}\right] }{q'}-\varepsilon _\mathsf {PRF}-\frac{1}{2^{\text {RSA}(k)}}\right) -{\varepsilon _\mathsf {PRF}}'-\frac{q'\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}}-\frac{10 k}{2^{k/2}}\\&\quad \ge \frac{1}{\text {RSA}(k)^2}\left( \frac{\varepsilon }{8 q' \text {RSA}(k)}-\varepsilon _\mathsf {PRF}-\frac{1}{2^{\text {RSA}(k)}}\right) -{\varepsilon _\mathsf {PRF}}'-\frac{q'\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}}-\frac{10 k}{2^{k/2}}. \end{aligned}$$

Now, by Theorem 5.6, our generic transformation from Sect. 3 applied to $\mathsf {SIG}^{\mathsf {RSA}}$yields an EUF-dnaCMA-secure signature scheme. Finally, we use chameleon hashing [23] to generically construct the fully secure scheme $\mathsf {SIG}_{\mathsf {gen}}^{\mathsf {RSA}}$, like for instance the RSA-based chameleon hash from [20, Appendix C].

5.4 Optimizations

The resulting signature scheme of the previous section $\mathsf {SIG}_{\mathsf {gen}}^{\mathsf {RSA}}$may be EUF-CMA secure but is not very compact yet. In addition to parameters for the chameleon hash, a signature of $\mathsf {SIG}_{\mathsf {gen}}^{\mathsf {RSA}}$consists of $l= \lfloor \log _{c}(k)\rfloor$ $\mathsf {SIG}^{\mathsf {RSA}}$signatures. This can be improved considerably to constant size signatures by generic aggregation.

Figure 7 depicts the resulting scheme $\mathsf {SIG}_{\mathsf {opt}}^{\mathsf {RSA}}$for the two parameters $l$ (which implicitly contains the granularity parameter $c$) and $m$. We still use $l$ tags (intuitively representing the $l$ instances of the original scheme) for signing and verification. However, the public key’s size depends only on $m$ (which is a fixed parameter), and the signature size is constant: we need one group element and randomness for the chameleon hash (which is typically also about the size of a group element). In addition to $\mathsf {PRF}^{\{0,1\}^{\text {RSA}(k)}}$, we now need functions $(\mathsf {PRF}^{\mathcal {T}_i})_{i \in [l]}$ to generate the tags for a signature. We can construct all of these functions from a single PRF $\mathsf {PRF}^{\{0,1\}^*}$ with sufficiently long output and use $\kappa \in \{0,1\}^k$ as its key.

Fig. 7

The optimized RSA-based signature scheme $\mathsf {SIG}_{\mathsf {opt}}^{\mathsf {RSA}}$

Theorem 5.7.

Let $F$be a PPT EUF-CMA adversary against $\mathsf {SIG}_{\mathsf {opt}}^{\mathsf {RSA}}$with advantage $\varepsilon \,{:=}\, \mathsf {Adv}^{\mathsf {euf\text{- }cma}}_{\mathsf {SIG}^{\mathsf {RSA}}, F}(k)$ asking for $q \,{:=}\, q(k)$ signatures (at most). Then, it can be used to efficiently solve an RSA challenge according to Definition 5.1 with probability at least

$$\begin{aligned}&\frac{1}{\text {RSA}(k)^2}\left( \frac{\varepsilon ^{c/m+ 1}}{2^{5 + c/m} \cdot q^{c+ c/m} \cdot \text {RSA}(k)} - \varepsilon _\mathsf {PRF}-\frac{1}{2^{\text {RSA}(k)}}\right) \\&\quad \quad - {\varepsilon _\mathsf {PRF}}' - {\varepsilon _\mathsf {PRF}}'' - \varepsilon _\mathsf {CH}- \frac{q\cdot l\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}} - \frac{10 k}{2^{k/2}} \end{aligned}$$

where $\varepsilon _\mathsf {PRF}$, ${\varepsilon _\mathsf {PRF}}'$, ${\varepsilon _\mathsf {PRF}}''$, and $\varepsilon _\mathsf {CH}$ are the success probabilities for breaking $\mathsf {PRF}$and $\mathsf {CH}$, respectively.

Proof.

Since the proof is very similar to the combination of proofs Theorems 3.3 and 5.6, we only describe the interesting parts. In addition, we omit the chameleon hash here and prove the EUF-dnaCMA security of the corresponding modified scheme (with $x \,{:=}\, M$ instead of $x \,{:=}\, \mathsf {CH}(M, r)$ and no randomness for the chameleon hash in the signature). The chameleon hash is then added at the end using generic arguments [23].

Again, w.l.o.g. we assume that the adversary will ask for exactly $q > 0$ signatures.

Setup Analogously to Theorem 3.3, we use the select algorithm to pick an ${i^*}$. Intuitively, ${i^*}$represents one of the $l$instances, and $\mathcal {T}_{i^*}$ is the set of tags used for this instance. We will embed the challenge only in this instance and simulate all the others.

We start off by picking a random key $\kappa$ for the PRF $\mathsf {PRF}$. For each queried message $(M_j)_{j\in [q]}$, we compute the tags $t_i^{(j)} \,{:=}\, \mathsf {Samp}(\mathcal {T}_i, \mathsf {PRF}_\kappa (M_j))$. Subsequently, we guess a tag $t_{i^*} \leftarrow \mathcal {T}_{i^*}$ and abort if the list of tags for the ${i^*}$th instance $(t_j^{({i^*})})_{j \in [q]}$ contains any tag more than $m$ times.

Next, we embed the challenge exponent. Like in Theorem 5.6, we set up $\mathsf {P}_{(\kappa ,b)}$such that $\mathsf {P}_{(\kappa ,b)}(t_{i^*}) = e^*=: {p^*}$ and abort if $\mathsf {P}_{(\kappa ,b)}(t_i^{(j)}) = {p^*}$ for any $t_i^{(j)} \not = t_{i^*}$. Afterward, we compute primes $p_i^{(j)} \,{:=}\, \mathsf {P}_{(\kappa ,b)}(t_i^{(j)})$ corresponding to the instance tags for $i \in l, j \in [q]$.

Finally and analogously to Theorem 5.6, we define two polynomials $f$ and $g$. For the construction of $f$, we use the messages $M_j$ with $t_{i^*}^{(j)} = t_{i^*}$. If there are no such messages, then we define $f(M) \,{:=}\, 1$. For $i \in [m]$, we set

$$\begin{aligned} u_i \,{:=}\, \left( y^{\pi _f \alpha _i + \pi _g \beta _i}\right) ^2, \end{aligned}$$

where $\pi _f$ is the product of all the primes for all instances computed above omitting occurrences of $p^*$and $\pi _g :=\pi _f\cdot {p^*}$.

Signing Signing works exactly like in Theorem 3.3: For the signature of $M_j$, we use the tags $(t_i^{(j)})_{i \in [l]}$. If $t_{i^*}^{(j)} = t_{i^*}$, then we make use of the fact that $f(M_j) = 0$ and sign by omitting the primes $(p_i^{(j)})_{i \in [l]}$ in $\pi _g$. Otherwise, if $t_{i^*}^{(j)} \not = t_{i^*}$, and hence, $p_i^{(j)} \not = {p^*}$ for $i \in [l]$, we can sign by omitting the corresponding factors in $\pi _f$ and $\pi _g$.

Extract from forgery Eventually, we receive a message $M^*$ and a forged signature $\sigma ^*$. If $\mathsf {Samp}(\mathcal {T}_{i^*}, \mathsf {PRF}_\kappa (M^*)) \not = t^*$, then we abort. Otherwise, if the adversary was successful, the verification equation holds, and we can, analogously to Theorem 5.6, compute

$$\begin{aligned} (\sigma / y^{2 \pi _f g(M)})^{p^*}\equiv y^{2 \pi _f f(M)}. \end{aligned}$$

Again, we need $\gcd ({p^*}, 2 \pi _f f(M)) = 1$ as a prerequisite for Shamir’s trick (Lemma 5.2). We can then compute a solution for the given RSA challenge.

Analysis The analysis is very similar to that of Theorem 5.6. The following differences occur:

• The chance for the simulator to guess the tag used for the forgery correctly is $\frac{1}{|\mathcal {T}_{i^*}|}$ instead of $\frac{1}{q'}$.

• More primes are computed using $\mathsf {P}_{(\kappa ,b)}$. All of these $q\cdot l$ primes must be distinct from $p^*$. Hence, instead of $q'$ in Theorem 5.6, Game 4, we have $q\cdot l$. However, the relevant probability is still negligible $\frac{q\cdot l\cdot {\text {RSA}(k)}}{2^{\text {RSA}(k)}}$ instead of $\frac{q\cdot {\text {RSA}(k)}}{2^{\text {RSA}(k)}}$.

• There is an additional abort if more than $m$ of the queried messages have the same tag in instance ${i^*}$. Analogously to Theorem 3.3, we lose ${\varepsilon _\mathsf {PRF}}''$ and $\frac{\varepsilon }{2}$ here.

Finally, we generically add a chameleon hash with the techniques of [23] to reach full security which reduces the success negligibly by $\varepsilon _\mathsf {CH}$ (the success of an adversary to produce a collision for the chameleon hash). Hence, the simulator is successful with probability at least

$$\begin{aligned}&\frac{1}{\text {RSA}(k)^2}\left( \frac{\varepsilon }{16 |\mathcal {T}_{i^*}|\text {RSA}(k)} - \varepsilon _\mathsf {PRF}-\frac{1}{2^{\text {RSA}(k)}}\right) - {\varepsilon _\mathsf {PRF}}' - {\varepsilon _\mathsf {PRF}}'' - \varepsilon _\mathsf {CH}\\&\quad - \frac{q\cdot l\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}} - \frac{10 k}{2^{k/2}} \\&\qquad \mathop {\ge }\limits ^{(*)}\frac{1}{\text {RSA}(k)^2}\left( \frac{\varepsilon ^{c/m+ 1}}{2^{5 + c/m} q^{c+ c/m}\text {RSA}(k)} - \varepsilon _\mathsf {PRF}-\frac{1}{2^{\text {RSA}(k)}}\right) - {\varepsilon _\mathsf {PRF}}' - {\varepsilon _\mathsf {PRF}}''\\&\quad \qquad -\,\varepsilon _\mathsf {CH}- \frac{q\cdot l\cdot \text {RSA}(k)}{2^{\text {RSA}(k)}} - \frac{10 k}{2^{k/2}}. \end{aligned}$$

Here, (*) holds; since by Lemma 3.5, we have $|\mathcal {T}_{i^*}| \le 2\cdot \left( \frac{2\cdot q^{m+1}}{\varepsilon }\right) ^{c/m}$.

6 Our SIS-Based Scheme

Let us now describe our SIS-based signature scheme. Again, we start with constructing a tag-based signature scheme and prove $\text {EUF-dnaCMA}_m^*$-security, but only for $m=1$. This scheme can be converted into a fully EUF-CMA secure signature scheme by applying the generic transformation from Sect. 3.

Note that in the previous chapters, we have used the character $m$ to denote the number of repeating tags in the $\text {EUF-dnaCMA}_m^*$security experiment. Unfortunately, the same character is commonly used in lattice-based cryptography to denote the dimension of a matrix ${\mathbb {Z}}_p^{n\times m}$. In order to be consistent with the literature, and since we consider only $\text {EUF-dnaCMA}_1^*$-security in the sequel, we will from now on use $m$ to denote the dimension of matrices.

6.1 Preliminaries

In this section, we summarize some known facts about lattices, as far as relevant for our signature scheme and its security analysis. The reader familiar with lattice-based cryptography, in particular with [1, 6, 8, 15], can safely skip this section.

6.1.1 Lattices and SIS

For positive integers $p,m,n$ and $A \in {\mathbb {Z}}_p^{n\times m}$, the $m$-dimensional integer lattices $\Lambda _p^\perp (A)$ and $\Lambda _p^u$ are defined as

$$\begin{aligned}&\Lambda _p^\perp (A)\,{:=}\,\{e \in {\mathbb {Z}}^m: Ae = 0 \,\,\hbox {mod}\,\,p\}\\&\Lambda _p^u(A)\,{:=}\,\{e \in {\mathbb {Z}}^m: Ae = u \,\,\hbox {mod}\,\,p\} \end{aligned}$$

Definition 6.1.

The $(p,n,m,\beta )$ -small integer solution (SIS) problem (in $\ell _2$-norm, denoted $\Vert \cdot \Vert$) is: given $p\in {\mathbb {N}}$, $A \in {\mathbb {Z}}_p^{n\times m}$, and $\beta \in {\mathbb {R}}$, find a non-zero vector $e \in {\mathbb {Z}}^m$ such that $Ae = 0 \,\,\hbox {mod}\,\,p$ and $\Vert e\Vert \le \beta$.

Fact 1.

(Theorem 4 of [1]) Let $p\ge 3$ be odd and let $m\ge 6n\log p$. There exists a probabilistic polynomial-time algorithm $\mathsf {TrapGen}$ that, on input $(p,n)$, outputs a matrix $A \in {\mathbb {Z}}_q^{n \times m}$ which is statistically close to uniform, and a basis $T_A$ of $\Lambda _p^\perp (A)$ such that $\Vert \tilde{T}_A\Vert \le \mathbf {O}(\sqrt{m})$, where $\tilde{T}_A$ denotes the Gram-Schmidt orthogonalization of $T_A$, and $\Vert T_A\Vert \le \mathbf {O}({m})$, with all but negligible (in $n$) probability.

Fact 2.

(Theorem 4.1 of [15]) Let $\mathcal {D}_{\Lambda ,\gamma ,c}$ denote the discrete Gaussian distribution over $\Lambda$ with center $c$ and parameter $\gamma$. Let $T_A$ be any basis of $\Lambda _p^\perp (A)$. There exists a probabilistic polynomial-time algorithm that takes as input $(A,T_A,c,\gamma )$ with $\gamma \ge \Vert \tilde{T_A}\Vert \cdot \omega (\sqrt{\log m})$, and output distribution of which is identical to $\mathcal {D}_{\Lambda _p^\perp (A),\gamma ,c}$ up to a negligible statistical distance.

To simplify our notation, we write $\mathcal {D}_{\Lambda _p^\perp (A),\gamma }$ for $\mathcal {D}_{\Lambda ,\gamma ,c}$ if $c=0$.

Fact 3.

(Lemma 4.4 of [26]) Let $e \leftarrow \mathcal {D}_{\Lambda _p^\perp (A),\gamma }$. Then, the probability that $\Vert e\Vert > \gamma \sqrt{m}$ is negligible (in $n$).

Fact 4.

(Algorithm SampleLeft of [1]) Let

• $A \in {\mathbb {Z}}_p^{n\times m}$ be a matrix of rank $n$, and $T_A$ be a (short) basis $\Lambda _p^\perp (A)$,

• $F\in {\mathbb {Z}}_p^{n\times m}$,

• $u \in {\mathbb {Z}}_p^n$ be a vector, and

• $\gamma \ge \Vert \tilde{T}_A\Vert \cdot \omega (\sqrt{\log m})$ be a Gaussian parameter.

There exists an efficient algorithm ${\mathsf {SmpL}}$ that takes as input $(A,T_A,F,u,\gamma )$, and outputs $e \in {\mathbb {Z}}_p^{2m}$ such that the distribution of $e$ is statistically close to $\mathcal {D}_{\Lambda _p^u(A|F),\gamma }$.

Fact 5.

(Algorithm SampleRight of [1])

Let

• $A,B \in {\mathbb {Z}}_p^{n\times m}$ be matrices, where $B$ has rank $n$ and $T_B$ is a (short) basis of $\Lambda _p^\perp (B)$:

• $\Delta \in {\mathbb {Z}}_p^{n\times n}$ be of full rank $n$;

• $R \in \{-1,1\}^{m\times m}$ be a random matrix, and $s_R \,{:=}\, \Vert R\Vert = \sup _{\Vert x\Vert =1} \Vert Rx\Vert$ (note that for random $R\in \{-1,1\}^{m\times m}$, we have $s_R \le \mathbf {O}(\sqrt{\log m})$ with overwhelming probability);

• $u \in {\mathbb {Z}}_p^n$ be a vector; and

• $\gamma \ge \Vert \tilde{T}_B\Vert \cdot s_R \cdot \omega (\sqrt{\log m})$ be a Gaussian parameter.

There exists an efficient algorithm ${\mathsf {SmpR}}$ that takes as input $(A,B,T_B,\Delta ,R,u,\gamma )$, and outputs $e \in {\mathbb {Z}}_p^{2m}$ such that the distribution of $e$ is statistically close to $\mathcal {D}_{\Lambda _p^u(A|F),\gamma }$, where $F \,{:=}\, AR + \Delta B$.

Fact 6.

(Lemma 13 of [1])

Let $p\in {\mathbb {N}}$ be an odd prime and let $m>(n+1)\log p+ \omega (\log n)$. Let $R \leftarrow \{-1,1\}^{m\times m}$ and $A,A' \leftarrow {\mathbb {Z}}_p^{n\times m}$ be uniformly random. Then, the distribution of $(A,AR)$ is statistically close to the distribution of $(A,A')$.

Fact 7.

(Corollary 5.4 of [15], Fact 14 of [6])

Let pbe a prime and let $n,m$ be integers such that $m\ge 2n\log p$. Let $e \leftarrow \mathcal {D}_{{\mathbb {Z}}^m,\gamma }$, where $\gamma \ge \omega (\sqrt{\log m})$. Then, for all but at most a $2 p^{-n}$ fraction of all matrices $A \in {\mathbb {Z}}_p^{n\times m}$ the distribution of the syndrome $u \,{:=}\, Ae \,\,\hbox {mod}\,\,p$ is statistically close to uniform over ${\mathbb {Z}}_p^n$. Furthermore, the conditional distribution of $e$, given $u$, is $\mathcal {D}_{\Lambda _p^u(A),\gamma }$.

6.1.2 Full-Rank Difference Hashing

We will need a map $H : \mathcal {T}\rightarrow {\mathbb {Z}}_p^{n\times n}$ that allows to map tags from $\mathcal {T}$ to matrices in ${\mathbb {Z}}_p^{n\times n}$, with the property that the difference matrix $\Delta \,{:=}\, H(t)-H(t')$ has full rank for all $t,t' \in \mathcal {T}$ with $t\ne t'$.

Definition 6.2.

Let $p$ be prime, $n \in {\mathbb {N}}$ be a positive integer, and let $\mathcal {T}$ be a set. We say that a hash function $H : \mathcal {T}\rightarrow {\mathbb {Z}}_p^{n\times n}$ is a full-rank difference hash function, if $H$ is efficiently computable, and for all distinct $t,t' \in \mathcal {T}$ holds that the difference matrix $\Delta \,{:=}\, H(t)-H(t')$ has full rank.

The notion of full-rank difference hash functions was introduced in [1], together with a simple and elegant construction of such hash functions with domain $\mathcal {T}= {\mathbb {Z}}_p^n$, which is suitable for our purposes.

6.2 $\text {EUF-dnaCMA}_1^*$-Secure Signature Scheme

Our tag-based signature scheme $\mathsf {SIG_{t}^{SIS}}$ is described in Fig. 8. The scheme uses a full-rank difference hash function $H : \mathcal {T}\rightarrow {\mathbb {Z}}_p^{n \times n}$ , and the tag space is an arbitrary set $\mathcal {T}$ such that there exists a such a hash function (e.g., $\mathcal {T}\,{:=}\, {\mathbb {Z}}_p^n$, as in [1]). We use parameters $p,n,m\in {\mathbb {N}}$, where $p$ is prime, and $\gamma \in {\mathbb {R}}$, whose choice partially depends on our security analysis and is therefore deferred to Sect. 6.3. Correctness of this scheme follows from Fact 3.

Fig. 8

The tag-based SIS scheme

Theorem 6.3.

For each efficient adversary $F$ breaking the $\text {EUF-dnaCMA}_1^*$-security of $\mathsf {SIG_{t}^{SIS}}$as described in Fig. 8, we can construct an efficient algorithm $\mathsf {Sim}$ solving the $(p,n,m,\beta )$-SIS problem with $\beta = \mathbf {O}(\gamma m)$.

Scheme $\mathsf {SIG_{t}^{SIS}}$ exhibits many similarities to the identity-key generation algorithm of the IBE scheme from [1], where our tags correspond to identities of [1]. In the security proof, we simulate signatures in a way very similar to the identity-key generation in [1], by embedding an additional trapdoor in the matrix $G_t$ that allows us to simulate signatures for arbitrary messages and for all tags except for one tag $t_i = t^*$ which equals the tag from the forgery $(M^*,t^*)$ output by the forgery (since the tag-space is polynomially bounded, we can guess $t^*$ with nonnegligible probability). To this end, in the simulation matrix, $G_t$ is defined such that the additional trapdoor “vanishes” exactly for tag $t_i = t^*$.

The difference to the proof from [1] is that we must also be able to issue one signature for message-tag-pair $(M_i,t_i)$ with $t_i = t^*$, but without knowing any trapdoor. To simulate a signature for this message-tag pair, we define the vector $v$ contained in the public key as $v \,{:=}\, (A|G_{t_{i}}) e_{i} - UM_{i}$ for a random short vector $e_{i} \leftarrow \mathcal {D}_{{\mathbb {Z}}^{2m},\gamma }$. Note that this defines $v$ such that $e_{i}$ is a valid signature for message-tag-pair $(M_i,t_i)$.

A successful forger $F$has to produce a forgery $e^*$ for a message $M^* \ne M_i$, from which we obtain an equation $(A|G_{t_i}) e_i - UM_i = (A|G_{t_i}) e^* - UM^*$. By an adequate set-up of matrices $G_{t_i}$ and $U$, this equation allows us to extract a solution to the given SIS problem instance with high probability.

Proof.

For simplicity, let us assume a message length $\ell$ with $\ell =m$. The security proofs works identically for any $\ell \in [1,m]$.

$\mathsf {Sim}$ receives as input an SIS-challenge $A \in {\mathbb {Z}}_p^{n\times m}$, and runs $F$as a subroutine by simulating the $\text {EUF-dnaCMA}_1^*$-experiment for $F$. To this end, it proceeds as follows.

Start $\mathsf {Sim}$ starts $F(1^k)$ to receive a list $(M_1,t_1),\ldots ,(M_q,t_q)$ of $q$ chosen message-tag-pairs, where $t_i \ne t_j$ for all $i\ne j$.

Setup of the public key To create a public key, $\mathsf {Sim}$ chooses a full-rank difference hash function $H : \mathcal {T}\rightarrow {\mathbb {Z}}_p^{n\times m}$. Then, it runs the algorithm of Fact 1 to generate a matrix $B \in {\mathbb {Z}}_p^{n\times m}$ together with a short basis $T_B \subset \Lambda _p^\perp (B)$ with $\Vert \tilde{T}_B\Vert \le L$. Furthermore, it samples two random matrices $R_U,R_Z \leftarrow \{0,1\}^{m\times m}$, and defines matrices $U,Z,Y \in {\mathbb {Z}}_p^{n\times m}$ and vector $v \in {\mathbb {Z}}_p^{n}$ as

$$\begin{aligned} U \,{:=}\, AR_U, \quad Z \,{:=}\, AR_Z - H(t_{i^*})B, \quad Y \,{:=}\, B \in {\mathbb {Z}}_p^{n\times m}, \quad v \,{:=}\, (A|G_{t_{i^*}}) e_{i^*} - UM_{i^*} \end{aligned}$$

where $i^* \leftarrow [q]$ is chosen uniformly random, $e_{i^*} \leftarrow \mathcal {D}_{{\mathbb {Z}}^{2m},\gamma }$, $G_{t_{i^*}} \,{:=}\, Z + H(t_{i^*})Y$, and all computations are performed modulo $p$.

The public key is defined as $(U,A,Z,Y,v)$. Note that matrices $U,Z,Y$ are statistically close to uniform over ${\mathbb {Z}}_p^{n\times m}$ (due to Fact 6 and Fact 1), and $v$ is statistically close to uniform (due to Fact 7), thus this is a correctly distributed public key (up to a negligibly small statistical distance).

Simulating signatures A signature $\sigma _{i}$ for message-tag-pair $(M_i,t_i)$, $i \in [q]$, is computed as follows:

• Case $i \ne i^*$. In this case, we have

  $$\begin{aligned} G_{t_{i}} = AR_Z - H(t_{i^*})B + H(t_{i})B = AR_Z + \Delta B, \end{aligned}$$

  where $\Delta \,{:=}\, H(t_{i})-H(t_{i^*})$ is a full-rank matrix, since $H$ is a full-rank difference hash function. By running the algorithm from Fact 5 on input $(A,B,T_B,\Delta ,R_Z,u,\gamma )$, where $u \,{:=}\,$ $UM_i + v$, $\mathsf {Sim}$ computes a low-norm non-zero vector $e_i \leftarrow \mathcal {D}_{\Lambda _p^u,\gamma }$ satisfying

  $$\begin{aligned} (A|G_{t_i}) e_i = UM_i + v, \end{aligned}$$

  and sets $\sigma _i \,{:=}\, (e_i,t_i)$, which thus is a valid signature.

• Case $i = i^*$. Now, we have

  $$\begin{aligned} G_{t_{i^*}} = AR_Z - H(t_{i^*})B + H(t_{i^*})B = AR_Z, \end{aligned}$$

  thus $\mathsf {Sim}$ is not able to use the trapdoor $T_B$ to simulate a signature, since $B$ “vanishes”. However, in this case, $\mathsf {Sim}$ can set $\sigma _{i^*} \,{:=}\, (e_{i^*},t_{i^*})$. Recall that we have defined $v \,{:=}$ $(A|G_{s_{i^*}}) t_{i^*} - UM_{i^*}$ in the setup phase, thus

  $$\begin{aligned} (A|G_{t_{i^*}}) e_{i^*} = UM_{i^*} + v \qquad \iff \qquad (A|G_{t_{i^*}}) e_{i^*} - UM_{i^*}= v. \end{aligned}$$

  Note that $e_{i^*}$ is correctly distributed due to Fact 7, and we have $t_i \ne t_j$ for all $i \ne j$, thus $e_{i^*}$ is contained in exactly one signature. Note also that this is the case where our construction and proof differ from [6], since in [6], it is never necessary to simulate a signature in the case where matrix $B$ “vanishes,” due to a different construction and security experiment.

In either case, $\mathsf {Sim}$ is able to compute a valid and correctly distributed signature for each $i \in [q]$, and thus simulates the $\text {EUF-dnaCMA}_1^*$security experiment properly. By assumption, $F$will thus output $(M^*,(e^*,t^*))$, where $t^* = t_i$ for some $i \in [q]$ and $(e^*,t^*)$ is a valid signature for $M^* \not \in \{M_1,\ldots ,M_q\}$, with nonnegligible probability.

Extracting the SIS solution Suppose that $i = i^*$, which happens with probability $1/q$. Note that in this case it holds that

$$\begin{aligned} (A|G_{t^*}) e_{i^*} - UM_{i^*}&= v = (A|G_{t^*}) e^* - UM^* \\&\iff \\ (A|AR_Z) e_{i^*} - AR_UM_{i^*}&= v = (A|AR_Z) e^* - AR_UM^*\\&\iff \\ (A|AR_Z) (e_{i^*}-e^*)&- AR_U(M_{i^*}-M^*) = 0. \end{aligned}$$

Let us write vector $\hat{e} \,{:=}\, (e_{i^*}-e^*) \in {\mathbb {Z}}_p^{2m}$ as $\hat{e}^\top = (\hat{e}_1^\top , \hat{e}_2^\top )$ for two vectors $\hat{e}_1,\hat{e}_2 \in {\mathbb {Z}}_p^m$, and let us write $\hat{M}\,{:=}\, (M^*-M_{i^*}) \in \{-1,0,1\}^m$. Then, the above equation is equivalent to

$$\begin{aligned} A\hat{e}_1 + AR_Z\hat{e}_2 + AR_U\hat{M}= 0 \iff A(\hat{e}_1 + R_Z\hat{e}_2 + R_U\hat{M}) = 0. \end{aligned}$$

Algorithm $\mathsf {Sim}$ computes and outputs $e \,{:=}\, (\hat{e}_1 + R_Z\hat{e}_2 + R_U\hat{M})$ as solution to the given SIS challenge. It remains to show that $e$ is sufficiently short and non-zero with high probability.

Note that we have $\Vert \hat{e}_1\Vert \le \Vert \hat{e}\Vert \le 2 \cdot \gamma \sqrt{m}$, and similarly $\Vert \hat{e}_2\Vert \le 2 \cdot \gamma \sqrt{m}$. Note furthermore that $\Vert \hat{M}\Vert \le \sqrt{m}$. By [1, Lemma 15] it furthermore holds that $\Vert R_U\Vert \le 12\sqrt{2m}$ and $\Vert R_Z\Vert \le 12\sqrt{2m}$, except for a negligibly small probability. In summary, we thus have

$$\begin{aligned} \Vert e\Vert = \Vert \hat{e}_1 + R_Z\hat{e}_2 + R_U\hat{M}\Vert&\le \Vert \hat{e}_1\Vert + \Vert R_Z\Vert \cdot \Vert \hat{e}_2\Vert + \Vert R_U\Vert \cdot \Vert \hat{M}\Vert \\&\le 2 \gamma \sqrt{m} + 24 \cdot \sqrt{2} \cdot m\gamma + 24 \cdot \sqrt{2} \cdot m \\&= \mathbf {O}(m\gamma ). \end{aligned}$$

Finally, let us show that $e \ne 0$ with high probability. Note that we must have $\hat{M}= M_{i^*} - M^* \ne 0 \in \{-1,0,1\}^m$, since $M_{i^*} \ne M^*$. Note furthermore that $F$ does not receive $R_Z$ and $R_U$ explicitly as input, but only implicitly as $(A,AR_Z,AR_U)$.

We will show a slightly stronger result than necessary, namely that even any unbounded algorithm $\Gamma$, which receives as input $(A,R_Z,AR_U)$ (i.e., $R_Z$ in explicit form), will output $\hat{e}_1,\hat{e}_2, \hat{M}$ such that $e \,{:=}\, \hat{e}_1 + R_Z \hat{e}_2 + R_U \hat{M} \ne 0$ with significant probability. Since $R_Z$ is given explicitly, we may simplify this to

$$\begin{aligned} R_U \hat{M}= \delta \in {\mathbb {Z}}_p^n, \end{aligned}$$

where $\hat{M}\ne 0$ and $\delta \,{:=}\, -\hat{e}_1 - R_Z \hat{e}_2$ are chosen by $\Gamma$. Writing $R_U = (r_1,\ldots ,r_m) \in \{0,1\}^{m\times m}$ for vectors $r_i \in \{0,1\}^m$ and $\hat{M}= (\hat{M}_1,\ldots ,\hat{M}_m)^\top$, we can write this equivalently as

$$\begin{aligned} \delta = R_U \hat{M}=\sum _{i=1}^mr_i \hat{M}_i = r_j \hat{M}_j + \sum _{i=1,i \ne j}^mr_i \hat{M}_i \in {\mathbb {Z}}_p^n, \end{aligned}$$

where $\hat{M}_j \in \{-1,1\}$ is an arbitrary non-zero component of $\hat{M}$ (note that there must be at least one non-zero component, since $\hat{M}\ne 0 \in {\mathbb {Z}}_p^n$).

Recall that $\Gamma$ receives only implicit information about $R_U$, in form of $AR_U$. If we can show that there exist two possible choices $r_j,r_j' \in \{-1,1\}^m$ such that $r_j \ne r_j'$ which are equally likely in the view of $\Gamma$, then clearly we must have $\Pr [e \ne 0] \ge 1/2$, because

$$\begin{aligned} r_j \ne r_j' \quad \implies \quad r_j \hat{M}_j + \sum _{i=1,i \ne j}^mr_i \hat{M}_i \ne r_j' \hat{M}_j + \sum _{i=1,i \ne j}^mr_i \hat{M}_i. \end{aligned}$$

Note that $AR_U = (Ar_1|\cdots |Ar_m)$. Thus, we need to show that with overwhelming probability there exists $r_j,r_j' \in \{-1,1\}^m$ with

$$\begin{aligned} Ar_j = Ar_j' \in {\mathbb {Z}}_p^n. \end{aligned}$$

Let $f_A(r) : \{-1,1\}^m\rightarrow {\mathbb {Z}}_p^n$ be the map $r \mapsto Ar$. By the pigeonhole principle there are at most $p^n-1$ vectors $r$ in $\{-1,1\}^m$ such that the value $f_A(r) = Ar \in {\mathbb {Z}}_p^n$ has a unique preimage. Since $r_j$ is chosen uniformly random from $\{-1,1\}^m$, the probability that $r_j$ is one of those vectors is at most $(p^n-1)/2^m\le 2^{-m+ n\log p}$, which is negligible in $n$ if $m\ge 2 n\log p$.

Thus, with overwhelming probability there exist at least two vectors $r_j,r_j'$ with $r_j \ne r_j'$ that are consistent with the view of $\Gamma$, and thus equally likely, and therefore any algorithm $\Gamma$ will output $(\hat{e}_1,\hat{e}_2,\hat{M})$ with $\hat{e}_1 + R_Z \hat{e}_2 + R_U \hat{M} \ne 0$ with probability at least $1/2 - 2^{-m + n\log p}$.$\square$

6.3 Selection of Parameters

For the scheme to work correctly, we set $n\,{:=}\, k$, where $k$ is the security parameter. Furthermore, we need to ensure that

• ${\mathsf {TrapGen}}$ can operate, that is, we have $m\ge 6n\log p$,

• $\gamma$ is chosen such that the sampling algorithms from Facts 2, 4; and 5 produce the required distribution, and that Fact 7 applies, i.e., that $\gamma \ge m \cdot \omega (\sqrt{m})$,

• the worst-case to average-case reductions for SIS [15, 26] apply, i.e., we have $p\ge \beta \cdot \omega (n\log n)$, and

• the SIS solutions produced in the reduction are sufficiently short, that is, $\beta \ge \mathbf {O}(m\gamma )$.

6.4 EUF-CMA-Secure Scheme

By applying the generic transformation from Sect. 3 to our lattice-based $\text {EUF-dnaCMA}_1^*$-secure signature scheme, we obtain EUF-dnaCMA-secure signatures. Concretely, suppose we use message space $\{0,1\}^\ell$ with $\ell = m$. Then, the resulting EUF-dnaCMA-secure signature scheme has public keys consisting of $4nm+ n$ elements of ${\mathbb {Z}}_p$ plus a key $\kappa$ for the $\mathsf {PRF}$. Signatures consist of $l$ low-norm vectors in ${\mathbb {Z}}_p^n$, where $l = \lfloor \log _c(k) \rfloor = \mathbf {O}(\log k)$ is defined as in Sect. 3. The resulting scheme is depicted in Fig. 9.

Fig. 9

The EUF-naCMA-secure SIS scheme

Unfortunately, we are not able to aggregate signatures, like we did for the optimized CDH- and RSA-based constructions, due to the lack of signature-aggregation techniques for lattice-based signatures. We leave this as an interesting open problem.

To obtain a fully EUF-CMA-secure signature scheme, it suffices to combine the scheme from Fig. 9 with a suitable chameleon hash function, like, for instance, the SIS-based construction from [8, Sect. 4.1]. This chameleon hash adds another $2mn$ elements of ${\mathbb {Z}}_p$ to the public key, plus one additional low-norm vector $e \in {\mathbb {Z}}_p^m$ to each signature.