Bayesian modeling of bathtub shaped hazard rate using various Weibull extensions and related issues of model selection

Abstract

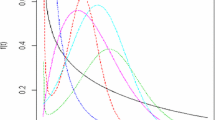
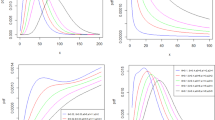
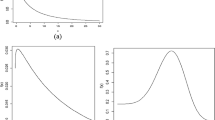
Bathtub shape is one of the most important behaviors of the hazard rate function that is quite common in lifetime data analysis. Such shapes are actually the combination of three different shapes and, as such, there have been several proposals to model such behavior. One such proposal is to combine at most three different distributions, often the Weibull or some similar model, separately for decreasing, constant, and increasing shapes of the hazard rate. Sometimes combination of two different models may also result in the required bathtub shape. The other proposal includes generalizing or modifying the two-parameter distribution by adding an extra parameter into it. It is often seen that the first proposal is quite cumbersome whereas the second fails to capture some important aspects of the data. The present work considers two recent generalizations/modifications of the two-parameter Weibull model, namely the Weibull extension and the modified Weibull models, and proposes mixing the two families separately with the three-parameter Weibull distribution in order to see if the mixing results in some real benefit though at the cost of too many parameters. The paper finally considers the complete Bayes analysis of the proposed models using Markov chain Monte Carlo simulation and compares them with both Weibull extension and the modified Weibull models in a Bayesian framework. It is observed that the mixture models offer drastic improvement over the individual models not only in terms of hazard rate but also in terms of overall performance. The results are illustrated with the help of a real data based example.

Appendices

Appendix

Following algorithm was used to generate iteratively the parameter θ and the missing data z from π (θ ∣ x, z) and f (z∣x, θ), respectively.

Let $\theta^0=\left( {\theta_1^{\left( 0 \right)} ,\theta_2^{\left( 0 \right)} \ldots\ldots \theta _{r}^{\left( 0 \right)}} \right)$ be the initial starting values in the iteration scheme then the algorithm at ‘t ^th’ step can be written as,

(i):

generate z ^(t) ∼ f (z ∣ x, θ ^(t)).

(ii):

generate θ ^(t + 1) ∼ π(θ ∣ x, z ^(t)).

where f(z ∣ x, θ ^(t)) is a multinomial distribution with weights given by $\frac{p_j^{\left( t \right)} {f}_{j}^{\left({t} \right)} \left( {x_i} \right)}{\sum\limits_{l=1}^k {p_l^{\left( t \right)} {f}_{l}^{\left({t} \right)} \left( {x_i} \right)} }$, j = 1,2, . . . ,k, i = 1,2, . . . ,n, and π(θ|x, z) is used to denote the posterior of θ.

We have two mixture models, namely WEWM and MWWM, each having two components with mixing proportion p and 1 − p and, therefore, it would be more convenient to define z _ij such that z _i  = z _i1 and 1 − z _i  = z _i2 for i = 1, 2,...,n. In this case f(z ∣ x, θ ^(t)) becomes simply binomial distribution with weights p ^∗ and 1 − p ^∗, where

$${p}^\ast =\frac{p^{\left({t} \right)}{f}_1^{\left({t} \right)} \left( {x_i} \right)}{p^{\left({t} \right)}{f}_1^{\left({t} \right)} \left( {x_i} \right)+\left( {1-p} \right)^{\left({t} \right)}{f}_2^{\left({t} \right)} \left( {x_i} \right)}. $$

Generation from π(θ ∣ x, z ^(t)) in step (ii) can be achieved using any of the MCMC procedures. To explore, let us write the full conditionals corresponding to each of the two mixture models so that the possibility of working in one dimension can be thought of. It is to be noted that if all the full conditionals are easily available where available is taken to mean that samples can be efficiently and straightforwardly generated, the generation from π (θ ∣ x, z ^(t)) reduces to simply Gibbs sampler implementation. In case a full conditional is difficult to run, one can apply Metropolis algorithm as a mixing strategy with the Gibbs sampler.

Full conditionals and generating algorithms for WEWM model

$$ f_{11} \left( {p\left| {\alpha_1, \beta_1} \right.,\lambda_1, \alpha, \beta, \mu} \right)\propto {p}^{\sum\limits_{i=1}^n {{z}_{i}} +a-1} \left( {{1-p}} \right)^{\left( {n-\sum\limits_{i=1}^n {z_i} } \right)+b-1}, $$

(A1)

$$ \begin{array}{rll} &&f_{12} \left( {\alpha_1 \left| {p,\beta_1, \lambda_1, \alpha, \beta }, \right.\mu} \right)\\ &&\quad\propto \alpha _1^{\phi_1 -\left( {1 \mathord{\left/ {\vphantom {1 {\beta_1} }} \right. \kern-\nulldelimiterspace} {\beta_1} } \right)\sum\limits_{i=1}^n {z_i} -1} \mathrm{exp}\left\{ {{-}\lambda_1 \alpha _1^{\left( {{1-1} \mathord{\left/ {\vphantom {{1-1} {\beta_1} }} \right. \kern-\nulldelimiterspace} {\beta_1} } \right)} \sum\limits_{i=1}^n {\left( {e^{\alpha_1 x_i} -1} \right)z_i} } \right\}\\ &&\qquad\times\exp \left( {\alpha_1 \sum\limits_{i=1}^n {x_i z_i} } \right) \exp \left({-\frac{\alpha_1} {\varphi_1} } \right), \end{array} $$

(A2)

$$ \begin{array}{rll} f_{13} \left( {\beta_1 \left| {p,\alpha_1, \lambda_1, \alpha, \beta }, \right.\mu} \right)&\propto& \beta_1^{\sum\limits_{i=1}^n {{z}_{i}} } \alpha_1^{-\left( {1 \mathord{\left/ {\vphantom {1 {\beta_1} }} \right. \kern-\nulldelimiterspace} {\beta_1} } \right)\sum\limits_{i=1}^n {z_i} } \prod\limits_{{i}={1}}^{n} {{x}_{i}^{\left( {\beta_1 -1} \right)z_i} } \\ &&\quad\times\mathrm{exp}\left\{ {{-}\lambda_1 \alpha_1^{\left( {{1-1} \mathord{\left/ {\vphantom {{1-1} {\beta_1} }} \right. \kern-\nulldelimiterspace} {\beta_1} } \right)} \sum\limits_{i=1}^n {\left( {e^{\alpha_1 x_i} -1} \right)z_i} } \right\}, \end{array} $$

(A3)

$$f_{14} \left( {\lambda_1 \left| {p,\alpha_1, \beta_1, \alpha, \beta }, \right.\mu} \right)\propto \lambda_1^{\sum\limits_{i=1}^n {z_i} } \mathrm{exp}\left\{ {{-}\lambda_1 \alpha_1^{\left( {{1-1} \mathord{\left/ {\vphantom {{1-1} {\beta_1} }} \right. \kern-\nulldelimiterspace} {\beta_1} } \right)} \sum\limits_{i=1}^n {\left( {e^{\alpha_1 x_i} -1} \right)z_i} } \right\}, $$

(A4)

$$ \begin{array}{rll}f_{15} \left( {\alpha \left| {p,\alpha_1, \beta_1, \lambda_1, \beta }, \right.\mu} \right)&\propto & {\alpha}^{\eta +\left( {\sum\limits_{i\in A} {\left( {1-z_i} \right)}} \right)-1}\\ &&\times \,\exp \left\{{-{\alpha} \left( {\sum\limits_{i\in A} {\left( {x_i -{\mu}} \right)^{\beta} \left( {1-z_i} \right)} } \right)+\frac{1}{\kappa}} \right\}, \end{array} $$

(A5)

$$ \begin{array}{rll}f_{16} \left( {\beta \left| {p,\alpha_1, \beta_1, \lambda_1, \alpha }, \right.\mu} \right)& \propto &\beta^{\sum\limits_{i\in A} {\left( {1-z_i} \right)}} \prod\limits_{i\in A} {\left( {{x}_{i} -\mu} \right)^{\left( {\beta -1} \right)\left( {1-z_i} \right)}} \\ &&\quad\times\mathrm{exp}\left\{ {{-}\alpha \sum\limits_{i\in A} {\left( {x_i -\mu} \right)^{\beta} \left( {1-z_i} \right)}} \right\}, \end{array} $$

(A6)

$$ \begin{array}{rll} f_{17} \left( {\mu \left| {p,\alpha_1, \beta_1, \lambda_1, \alpha }, \right.\beta} \right)& \propto& \prod\limits_{i\,\in A} {\left( {{x}_{i} -\mu} \right)^{\left( {\beta -1} \right)\left( {1-z_i} \right)}} \\ &&\quad\times\mathrm{exp}\left\{ {{-}\alpha \sum\limits_{i\in A} {\left( {x_i -\mu} \right)^{\beta} \left( {1-z_i} \right)}} \right\}; \end{array} $$

(A7)

where $\tau \le \mu \le \min \left\{ {A_x} \right\}=x_k$ (say). It can be seen that the full conditionals (A4) and (A5) are gamma distributions and any gamma generating routine can be used to generate variates from these (see Devroye, 1986). Generation from (A2) and (A3) is a bit complicated and no straightforward generation scheme appears applicable. We considered Metropolis algorithm with suitably centered and scaled univariate normal density as a candidate generating density for the Metropolis implementation (see, for example, Upadhyay, Vasishta and Smith, 2001). Full conditional (A6) is a log-concave density and adaptive rejection algorithm of Gilks and Wild (1992) can be successfully employed for generating from it. A(1) is a beta distribution and generation from it is quite routine.

Generation of μ can be achieved by using rejection sampling through specially designed envelop density for it. We used envelop density g(μ) as

$$ g\left( \mu \right)=\left( {{1}+\left( {\beta {-1}} \right)\left( {{1-z}_{k}} \right)} \right)\frac{\left( {{x}_{k} -\mu} \right)^{\left( {\beta {-1}} \right)\left( {{1-z}_{k}} \right)}}{\left( {x_{k} -\tau} \right)^{\left( {\beta {-1}} \right)\left( {{1-z}_{k}} \right)+{1}}}{, } \tau \le \mu \mathrm{ } \le \mathrm{min}\left\{ {{A}_{x}} \right\}{.} $$

Full conditionals and generating algorithms for MWWM model

$$ f_{21} \left( {p\left| {\alpha_2, \beta_2} \right.,\lambda_2, \alpha, \beta, \mu} \right)\propto { p}^{\sum\limits_{i=1}^n {{z}_{i}} +a-1}\mathrm{ } \left( {{1-p}} \right)^{^{\left( {n-\sum\limits_{i=1}^n {z_i} } \right)+b-1}}, $$

(B1)

$$ \begin{array}{rll} f_{22} \left( {\alpha_2 \left| {p,\beta_2, \lambda_2, \alpha, \beta }, \right.\mu} \right)&\propto& \alpha_2^{\phi_2 +\sum\limits_{i=1}^n {z_i} -1} \\ &&\quad\times\exp \left[ {-\alpha_2 \left( {\sum\limits_{i=1}^n {x_i^{\beta_2} e^{\lambda_2 x_i} z_i} +\frac{\alpha_2} {\varphi_2} } \right)} \right], \end{array} $$

(B2)

$$ \begin{array}{rll} f_{23} \left( {\beta_2 \left| {p,\alpha_2, \lambda_2, \alpha, \beta, } \right.\mu} \right)&\propto &\prod\limits_{i=1}^n {\left\{ {\left( {\beta_2 +\lambda_2 \cdot x_i} \right)\cdot x_i^{\beta_2 -1}} \right\}^{z_i} }\\ &&\quad\cdot \exp \left[ {-\alpha_2 \sum\limits_{i=1}^n {x_i^{\beta_2} \exp \left( {\lambda_2 x_i} \right)} \mathrm{ }z_i} \right] \end{array} $$

(B3)

$$ \begin{array}{rll} f_{24} \left( {\lambda_2 \left| {p,\alpha_2, \beta_2, \alpha, \beta }, \right.\mu} \right)&\propto & \prod\limits_{i=1}^n \left( {\beta_2 +\lambda_2 \cdot x_i} \right)^{z_i} \cdot \exp \{\lambda_2 \sum\limits_{i=1}^n {x_i z_i} )\\ &&\cdot \exp \left[ {-\alpha_2 \sum\limits_{i=1}^n {x_i^{\beta_2} \exp \left( {\lambda_2 x_i} \right)} z_i} \right], \end{array} $$

(B4)

$$ \begin{array}{rll} f_{25} \left( {\alpha \left| {p,\alpha_2, \beta_2, \lambda_2, \beta }, \right.\,\mu} \right)&\propto & \alpha ^{\eta +\left( {\sum\limits_{i\in A} {\left( {1-z_i} \right)}} \right)-1}\\ &&\times\exp \left\{ {-\alpha \left( {\sum\limits_{i\in A} {\left( {x_i -\mu} \right)^{\beta} \left( {1-z_i} \right)}} \right)+\frac{1}{\kappa} } \right\}, \end{array} $$

(B5)

$$ \begin{array}{rll} f_{26} \left( {\beta \left| {p,\alpha_2, \beta_2, \lambda_2, \alpha }, \right.\,\mu} \right)&\propto &\beta^{\sum\limits_{i\in A} {\left( {1-z_i} \right)}} \mathrm{ } \prod\limits_{i\in A} {\left( {{x}_{i} -\mu} \right)^{\left( {\beta -1} \right)\left( {1-z_i} \right)}} \\ &&\times\mathrm{exp}\left\{ {{-}\alpha \sum\limits_{i\in A} {\left( {x_i -\mu} \right)^{\beta} \left( {1-z_i} \right)}} \right\}, \end{array} $$

(B6)

$$ \begin{array}{rll} f_{27} \left( {\mu \left| {p,\alpha_2, \beta_2, \lambda_2, \alpha }, \right.\beta} \right)&\propto &\prod\limits_{i\,\in A} {\left( {{x}_{i} -\mu} \right)^{\left( {\beta -1} \right)\left( {1-z_i} \right)}} \\ &&\times\mathrm{exp}\left\{ {{-}\alpha \sum\limits_{i\in A} {\left( {x_i -\mu} \right)^{\beta} \left( {1-z_i} \right)}} \right\}, \end{array} $$

(B7)

where $\tau \le \mu \mathrm{ } \le \min \left\{ {A_x} \right\}$. It is clear that full conditionals (B1), (B5), (B6) and (B7) are similar to (A1), (A5), (A6) and (A7) and, therefore, generation schemes for the corresponding variates remain the same. Full conditionals (B3) and (B4) can be shown to be log-concave and generation of corresponding variates can be done using adaptive rejection algorithm (see Gilks and Wild, 1992). Finally, (B2) is a gamma density and any standard gamma generating algorithm can be used to generate variates from this full conditional. We used a gamma generating routine given in Devroye (1986).