Abstract
This paper introduces a deterministic fluid model that approximates the many-server G t /GI/s t +GI queueing model, and determines the time-dependent performance functions. The fluid model has time-varying arrival rate and service capacity, abandonment from queue, and non-exponential service and patience distributions. Two key assumptions are that: (i) the system alternates between overloaded and underloaded intervals, and (ii) the functions specifying the fluid model are suitably smooth. An algorithm is developed to calculate all performance functions. It involves the iterative solution of a fixed-point equation for the time-varying rate that fluid enters service and the solution of an ordinary differential equation for the time-varying head-of-line waiting time, during each overloaded interval.
Simulations are conducted to confirm that the algorithm and the approximation are effective.
Similar content being viewed by others
1 Introduction
Motivated by the need for tools to improve the performance of large-scale service systems, such as customer contact centers and healthcare systems, we introduce and analyze a deterministic fluid model that serves as an approximation for the many-server G t /GI/s t +GI queueing model, which has customer abandonment (the+GI), time-varying arrival rate and staffing (the subscript t), unlimited waiting space, the first-come first-served service discipline and non-exponential service and patience distributions (the two GI’s); see [3, 38] and references therein for background on contact centers and healthcare systems, respectively. Abandonment is now recognized as an important feature, for example, see [13, 39]. Non-exponential service and patience distributions often do arise [8] and these features can strongly affect performance.
The analysis here applies to a system that alternates between overloaded (OL) and underloaded (UL) intervals. With time-varying arrival rates, such alternating behavior commonly occurs when it is difficult to dynamically adjust the staffing level in response to changes in demand. If the staffing cannot be changed rapidly enough, then system managers must choose fixed or nearly fixed staffing levels that respond to several levels of demand over a time interval. Then it may not be cost-effective to staff at a consistently high level in order to avoid overloading at any time. Then the fluid model introduced here may capture the essential performance.
Most queueing models are stochastic, because a primary cause of congestion is random fluctuation in arrivals and service. Deterministic fluid models can be useful when the systematic variation in the arrival rate and/or staffing dominates the stochastic variation in the arrivals and service, or at least is an important contributing factor. There is an established tradition of considering fluid models in queueing theory [15, 30]. The present paper directly extends [37], which developed a deterministic fluid model to approximate the steady-state performance of a stationary G/GI/s+GI queueing model. The accuracy of fluid models for capacity planning has been strongly supported by [5]. A novel feature here and in [37], compared to most fluid models, is that we consider a non-Markovian many-server fluid model, which involves two-parameter functions; e.g., the queue content at time t that has been in queue for a duration at most y, denoted by Q(t,y), as a function of both t and y; see (2). The abandonment rate function and service completion rate function are driven by patience and service hazard-rate functions; see (7) and (9).
Our main goal here is to contribute to the techniques for analyzing service systems with the important and realistic feature of time-varying arrivals and staffing; see [14] for background. By focusing on the time-varying fluid model, we extend important work by Mandelbaum, Massey and Reiman [27], which established many-server heavy-traffic fluid and diffusion limits for the time-varying Markovian M t /M t /s t +M t queueing model, and thus associated approximations; see also [28, 29]. We make a significant step beyond [27–29] by considering non-exponential service and patience distributions as well as time-varying arrival rates and staffing.
Just as in [27–29], the approximations here are intended for systems with many servers and high arrival rate, so that mathematical support can be provided by many-server heavy-traffic limits. For the stationary Markovian M/M/s+M model, such limits are established in [13]; for stationary non-Markovian models, such limits are established in [18, 19]. A limit for a discrete-time model with time-varying arrival rates is given in Sect. 6 of [37]. However, here we do not establish stochastic-process limits. Instead, we are directly concerned with the fluid model itself. It is important to recognize that the fluid model can be considered directly as a legitimate model in its own right. By focusing on a continuous divisible quantity, which we call “fluid,” our fluid model is a special case of a storage or dam model, as in [32].
Even though we do not establish stochastic-process limits here, the results here play an important role in subsequent papers [22, 23] in which we do establish such many-server heavy-traffic limits. The paper [22] establishes both a functional weak law of large numbers (FWLLN), showing convergence to the fluid model considered here, and a functional central limit theorem (FCLT), providing mathematical support for a refined Gaussian approximation, in the case of exponential service. The paper [23] establishes a FWLLN for the more general case of GI service. The proofs of the FWLLN’s (Theorem 4.1 in [22]) use the compactness approach, proving that the sequence is tight and that all convergent subsequences converge to the same limit. Theorem 3 here plays an important role in uniquely characterizing the limit of all convergent subsequences; see Sect. 6.6.2 of [22] for that part of the proof. The results in [22, 23] also rely heavily on recent heavy-traffic limits for infinite-server queues in [31]. The connection to infinite-server queues plays a critical role here as well; see Sects. 4, 5 and 7.1.
This paper makes important contributions even for the stationary G/GI/s+GI fluid model introduced in [37]. Here we provide for the first time a full description of the transient behavior. The fundamental evolution equations, in (5) here, are the same as in (2.14) and (2.15) of [37], but the time-dependent performance when the system is overloaded actually depends on three features introduced for the first time here. First, for non-exponential service, the time-varying rate that fluid enters service is characterized as the unique solution to a fixed-point equation; see (18) and Theorem 2. Second, the head-of-line waiting time is characterized here as the solution of an ordinary differential equation (ODE); see Theorem 3. Third, the potential waiting time, i.e., the virtual waiting time of an arrival at time t if that arrival would elect never to abandon, is characterized as the unique solution of an equation involving the head-of-line waiting time or by yet another ODE; see Theorems 5 and 6. To the best of our knowledge, none of this structure has been exposed previously.
There is an important modeling issue when we consider time-varying staffing. We need to carefully specify what happens when the service capacity is scheduled to decrease when all servers are busy. Do we require that customers in service stay in service with the same server until their service is complete? (Our analysis here applies to the case in which we allow the service in progress to be handed off to another available server.) Even with such server-assignment switching, there are issues: Do we alter the prescribed staffing function to avoid forcing a customer out of service? If we adhere to the given staffing function, as assumed here, then some customers are necessarily forced out of service in the stochastic system. (That can be prevented in the idealistic deterministic fluid model; see Assumption 4 and Sect. 9.) In the stochastic system, when customers are forced out of service, which customers are forced out and what happens to them? Are these customers forced out of the system entirely? If so, is there service complete or do they retry? If customers are pushed back into the queue (as implicitly assumed in [27]), then where do they go in the queue, and what is their new abandonment behavior? Under regularity conditions, these realistic features will be asymptotically negligible in a many-server heavy-traffic limit, but these new considerations complicate the proof.
For the fluid model we directly assume feasibility of the staffing function, but in Sect. 9 we show how to detect the first violation of feasibility of a staffing function and how to find the minimum feasible staffing function greater than or equal to the initial staffing function if that one is infeasible. In Sect. 10 we show how to construct a staffing function to stabilize delays at any fixed target value, contributing to prior work in [12, 17].
The results have significant relevance for applications. First, service systems typically have arrival rates that vary significantly over time, and the results dramatically reveal the consequence, e.g., showing how the peak congestion lags behind the peak arrival rate, as discussed for the M t /GI/∞ stochastic model in [10, 11]. Second, service systems often do have non-exponential service and patience distributions [8], and the results dramatically reveal the consequence. From [25, 36, 37, 39], we know that the patience distribution beyond its mean has a significant impact. However, [36, 37] show that the steady-state performance in the stationary G/GI/s+GI model is relatively insensitive to the service-time cdf beyond its mean. In contrast, here we show that the service distribution beyond its mean can have a dramatic impact as well for the transient performance; see Sect. 2. Finally, the results in this paper have already been applied in [16] to create new effective real-time delay predictors for arriving customers in a service system with time-varying arrivals.
Here is how this paper is organized
We start in Sect. 2 by discussing an example, showing the results of the algorithm and how they compare to simulations of queueing systems. Next in Sect. 3 we carefully define the G t /GI/s t +GI fluid model and specify key regularity conditions. In Sect. 4 we state important scale-proportionality results, which provide important simplification for UL intervals. In Sect. 5 we characterize performance during a UL interval.
In Sect. 6 we characterize the service content density during an OL interval. Sections 6.1 and 6.2 are devoted to the special case of M service and non-M service, respectively. An explicit formula is available for M service; an iterative algorithm is developed for other cases. In Sect. 7 we characterize the queue performance functions. In Sect. 8 we summarize the resulting algorithm.
In Sect. 9 we show how to detect the first violation of feasibility of a staffing function and how to find the minimum feasible staffing function greater than or equal to any candidate one. In Sect. 10 we show how to construct a staffing function to stabilize delays at any fixed target value, In Sect. 11 we provide three postponed longer proofs, the proofs of Theorems 3, 5 and 6. Finally, in Sect. 12 we draw conclusions. Additional supporting material, including results of simulations, appears in a long appendix available online [24].
2 An example
We start with an example. We consider an M t /H 2/s+E 2 fluid model with a sinusoidal arrival-rate function: λ(t)=1+0.6sin(t), mean service time 1/μ=1, mean patience 1/θ=1, and fixed service capacity s=1. (We consider other examples in [24].) Specifically, we let the service distribution be a two-phase hyperexponential (H 2) with probability density function (pdf)

with parameters \(p=0.5(1-\sqrt{0.6})\), μ 1=2pμ and μ 2=2(1−p)μ, which produces squared coefficient of variation (variance divided by the square of the mean) c 2=4. We let the patience distribution be Erlang-2 (E 2) with pdf

The E 2 distribution has c 2=1/2.
We relate the fluid model to associated queueing models by exploiting many-server heavy-traffic scaling, as discussed in [13, 22, 27, 31, 37]. Thus, the corresponding queueing model with n servers will have arrival-rate function λ n (t)=nλ(t), s n =ns servers and the same service and patience distributions. Figure 1 shows plots of several key performance functions for 0≤t≤T≡17, starting out empty, together with the specified arrival rate λ(t): the head-of-line waiting time w(t), the fluid content in queue Q(t), the fluid content in service B(t), the total fluid content in system X(t)≡Q(t)+B(t), and the rate fluid enters service b(t,0). All performance functions are continuous except for the rate-into-service function b(t,0). In underloaded intervals, b(t,0)=λ(t); in overloaded intervals, b(t,0) is the unique solution of the fixed-point equation (18).
It is important that the fluid model provide useful approximations for stochastic queueing models. We apply simulation to show that the fluid approximation indeed is effective for that purpose. For very large queueing systems, the stochastic system behaves like the fluid model, having relatively small stochastic fluctuations. That is illustrated for an M t /H 2/s+E 2 queueing system with 2000 servers in Fig. 2. In the plot, the queueing content processes are scaled by dividing by n=2000, so that s remains at 1. For the actual queueing system, the quantities λ(t), Q(t), B(t), X(t) and b(t,0) should all be multiplied by n=2000.
Figure 2 actually shows three plots. It also shows the fluid approximation for the corresponding M t /M/s+E 2 model, having exponential service times with the same mean. For that alternative model, there is a more elementary algorithm, because it is not necessary to solve the fixed-point equation for b(t,0) in order to calculate b(t,x). Figure 2 shows two things: First, it shows that the simulation sample path for the M t /H 2/s+E 2 model agrees closely with the fluid performance. Second, Fig. 2 shows that the service distribution can make a big difference in the time-dependent performance. The performance of the fluid model changes significantly when we change the service distribution from H 2 to M (with the same mean); e.g., look at Q(t) at time t=3. (We do not show a simulation path for the M t /M/s+E 2 model, but it agrees closely with its fluid model for n=2000. See [24].)
The impact of the service distribution may be surprising, because a major conclusion of [36, 37] was that the steady-state performance is relatively insensitive to the service distribution beyond its mean. However, there is precedent for this phenomenon: In [9] we showed that the performance in the time-varying M t /GI/s/0 loss model depends quite strongly on the service distribution beyond its mean, even though the steady-state distribution of the stationary M/GI/s/0 loss model has the well known insensitivity property, concluding that the standard steady-state performance measures do not depend at all on the service distribution beyond its mean.
Figure 2 suggests that the periodic models approach a periodic steady state as time evolves; that is proved for the fluid model with M service in [21]. (We conjecture that is also true with GI service under minimal regularity conditions, but it has not yet been proved.) Figure 2 also shows that the impact of the service cdf G beyond its mean evidently is far greater at the beginning when the system is starting up, and then dissipates considerably as the system approaches its periodic steady state. That is consistent with intuition, because with H 2 service, there will be more very short service times and unusually long service times than would be the case of the exponential distribution. Hence, at the beginning starting empty, there are no old customers with long service times to compensate for many new customers with short service times in the H 2 case. As a consequence, the initial queue content is much less with H 2 than with M service. However, more supporting theory is needed.
Of course, most service systems have far fewer servers than the number n=2000 we considered. It is thus important that the fluid approximation can still be useful with fewer servers. With fewer servers, the stochastic fluctuations in the queueing stochastic processes play an important role. In that case, the fluid model can still be very useful by providing a good approximation for the mean values of the queueing stochastic processes. That is illustrated from the plot of the average of the scaled performance measures of 200 independent sample paths when there are only 30 servers in Fig. 3. We also consider the case n=15 in [24].
Work is in progress to investigate approximations for the full distributions at each time t, based on the new limits in [22]. A simple rough approximation for the distribution of X(t) based on the approximation for the mean here is a normal distribution with variance equal to the determined mean; that is consistent with the exact Poisson distribution with the M t /GI/∞ model (and thus the stochastically equivalent M t /M/s t +M model with θ=μ).
3 The fluid model
In this section we define the deterministic G t /GI/s t +GI fluid model and specify important regularity conditions. There is a service facility with finite capacity (staffing function) s≡{s(t):t≥0} that is set exogenously and enforced. There also is waiting space with unlimited capacity. There is a deterministic arrival process, with input directly entering the service facility if there is space available; otherwise the input flows into the waiting room. Fluid may leave the service facility only by completing service. However, fluid may leave the queue either by entering service or abandoning (leaving directly from the queue without receiving service). These flows are deterministic as well. The total input of fluid over the interval [0,t] is \(\varLambda (t) \equiv\int_{0}^{t} \lambda(u)\,du\), t≥0. We will be working with the time-dependent arrival-rate function λ≡{λ(t):t≥0}.
There are service-time and abandon-time cdf’s G and F, respectively, with pdf’s g and f, satisfying
Let \(\bar{G}\) and \(\bar{F}\) denote the associated complementary cdf’s (ccdf’s), defined by \(\bar{G}(x)\equiv1-G(x)\) and \(\bar{F}(x)\equiv1-F(x)\). We assume that the random service and abandon times are unbounded above, so that \(\bar{G} (x) > 0\) and \(\bar{F} (x) > 0\) for all x. We assume that the mean service time is 1; that choice is without loss of generality, because we can measure time in units of mean service times. In the fluid model, the cdf’s act as proportions. A proportion G(x) of any quantity of fluid completes service and departs within time x of the time it starts service; a proportion F(x) of any quantity of fluid abandons and departs without receiving service within time x of the time it arrives, provided that it has remained waiting in queue, and has not already been admitted to service.
The key performance descriptors are the two-parameter functions B(t,y) and Q(t,y): B(t,y) is the quantity of fluid in service at time t that has been in service for time less than or equal to y; Q(t,y) is the quantity of fluid waiting in queue at time t that has been in queue for time less than or equal to y. These functions will admit representations
where the fluid densities b and q are non-negative integrable functions. (See Proposition 2 in Sect. 5, Corollary 1 in Sect. 6.2, Proposition 6 in Sect. 7.1 and Corollary 5 in Sect. 7.2.)
Let Q(t)≡Q(t,∞) be the total fluid content in queue at time t, and let B(t)≡B(t,∞) be the total fluid content in service at time t. Let X(t)≡B(t)+Q(t) be the total fluid content in the system at time t.
To fully specify the model, we also need to specify the initial conditions, describing the system state at time 0. The initial conditions are specified by the two functions B(0,y) and Q(0,y), which are defined as above, and also satisfy (2) with densities b(0,x) and q(0,x). Thus, the G t /GI/s t +GI fluid model data consists of the six-tuple of functions (λ,s,F,G,b(0,⋅),q(0,⋅)).
We make several assumptions. The first is on the initial conditions.
Assumption 1
(Finite initial content)
B(0)<∞ and Q(0)<∞.
We develop a “smooth” model. For that purpose, let ℂ p be the set of piecewise-continuous real-valued functions, by which we mean that the function has only finitely many discontinuities in any finite interval, with left and right limits at each discontinuity point (within the interval); moreover, we assume that the function is right-continuous. Hence, \(\mathbb {C}_{p} \subseteq \mathbb {D}\), where \(\mathbb {D}\) is the space of right-continuous functions with left limits.
Assumption 2
(Smoothness)
s,Λ,F,G,B(0,⋅),Q(0,⋅) are differentiable functions with derivatives s′,λ,f,g,b(0,⋅),q(0,⋅) in ℂ p .
As a consequence of Assumption 2, Λ(t)<∞ for all t>0. (We use the fact that \(\mathbb {C}_{p} \subset \mathbb {D}\) here to deduce that λ is bounded over finite intervals; see p. 122 of [7]; that implies that Λ(t)<∞.) Together with Assumption 1, that implies that the finite-content property in Assumption 1 holds for all t: B(t)≤B(0)+Λ(t)<∞ and Q(t)≤Q(0)+Λ(t)<∞ for all t≥0.
Whenever Q(t)>0, we require there is no free capacity in service, i.e., B(t)=s(t). Also, whenever B(t)<s(t), then the queue is empty. These conditions are summarized in
Assumption 3
(Fluid dynamics constraints, FDC’s)
For all t≥0,
In general, there is no guarantee that a staffing function s is feasible; i.e., having the property that the staffing function is set exogenously and adhered to, without forcing any fluid that has entered service to leave without completing service, because we allow s to decrease. (The fluid is assumed to be incompressible.) We directly assume that the staffing function we consider is feasible, but we also indicate how to detect the first violation and then construct the minimum feasible staffing function greater than or equal to the given staffing function; see Sect. 9.
Assumption 4
(Feasible staffing)
The staffing function s is feasible, allowing all fluid that enters service to stay in service until service is completed; i.e., when s decreases, it never forces content out of service.
We now consider the service discipline. We let the service discipline in the fluid model be first-come first-served (FCFS). We remark that there is much less motivation for considering other service disciplines, such as processor-sharing, with many servers than with few servers, because a few long service times can only make those few (of many) servers unavailable to other customers.
Assumption 5
(FCFS service)
Fluid enters service in order of arrival.
As a consequence of Assumption 5, at time t there will be a boundary of the queue length density, which we call the boundary waiting time (BWT),
Clearly, first, w(t)≥0 and, second, w(t)>0 if and only if Q(t)>0. (Equation (4) is informal, because it is circular, with w depending on q, while q depends on w. We will carefully define and characterize the BWT w in Sect. 7.)
Based on the way the queueing system operates, we assume that q and b satisfy the following two fundamental evolution equations. Because of Assumption 5, fluid enters service from the queue from the right boundary of q(t,x).
Assumption 6
(Fundamental evolution equations)
For t≥0, x≥0 and u≥0,

The first equation in (5) says that the fluid in service that is not served remains in service (which requires that the staffing function be feasible, as in Assumption 4). The second equation in (5) says that the fluid waiting in queue that does not abandon and does not move into service, remains in queue.
Let v(t) be the potential waiting time (PWT) at t, i.e., the virtual waiting time at t for an arriving quantum of fluid that has unlimited patience. The virtual waiting time at time t is the actual waiting time if there is positive input at time t; otherwise it is the waiting time of hypothetical input if it were to occur at time t. In order to simplify the analysis of the two waiting time functions w and v, we make extra assumptions: These extra assumptions will be introduced in Sects. 7.2 and 7.3.
We now turn to the flows. Let A(t) be the total quantity of fluid to abandon in [0,t]; let E(t) be the total quantity of fluid to enter service in [0,t]; and let S(t) be the total quantity of fluid to complete service in [0,t]. Clearly we have the basic flow conservation equations
These totals are determined by instantaneous rates. To define those rates, let \(h_{G}(x)\equiv g(x)/\bar{G}(x)\) and \(h_{F}(x)\equiv f(x)/\bar{F}(x)\) be the hazard-rate functions of the service and abandonment-time distributions, respectively. Then



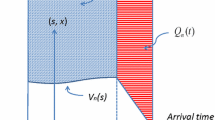
We have now completed the definition of the G t /GI/s t +GI fluid model (with the exception of (w,q,v), for which more is given in Sect. 7; Fig. 4 provides a pictorial summary. Our goal now is to fully characterize the six-tuple (b,q,w,v,σ,α) given the model parameters (λ,s,G,F) and the initial conditions {(b(0,x),q(0,x)):x≥0}, where q(0,x)>0 only if Q(0)>0, which in turn, by Assumption 3, can hold only if B(0)=s(0).
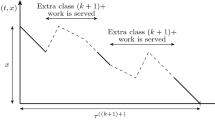
In doing so, we impose another regularity condition. We also assume that the system alternates between overloaded intervals and underloaded intervals, where these intervals include what is usually regarded as critically loaded. In particular, an overloaded interval starts at a time t 1 with (i) Q(t 1)>0 or (ii) Q(t 1)=0, B(t 1)=s(t 1) and λ(t 1)>s′(t 1)+σ(t 1), and ends at the overload termination time
Case (ii) in which Q(t 1)=0 and B(t 1)=s(t 1) is often regarded as critically loaded, but because the arrival rate λ(t 1) exceeds the rate that new service capacity becomes available, s′(t 1)+σ(t 1), we must have the right limit Q(t 1+)>0, so that there exists ϵ>0 such that Q(u)>0 for all u∈(t 1,t 1+ϵ). Hence, we necessarily have T 1>t 1.
An underloaded interval starts at a time t 2 with (i) B(t 2)<s(t 2) or (ii) B(t 2)=s(t 2), Q(t 2)=0, and λ(t 2)≤s′(t 2)+σ(t 2), and ends at underload termination time
As before, case (ii) in which Q(t 2)=0 and B(t 2)=s(t 1) is often regarded as critically loaded, but because the arrival rate λ(t 2) does not exceed the rate that new service capacity becomes available, s′(t 2)+σ(t 2), we must have the right limit Q(t 2+)=0. The underloaded interval may contain subintervals that are conventionally regarded as critically loaded; i.e., we may have Q(t)=0, B(t)=s(t) and λ(t)=s′(t)+σ(t). For the fluid models, such critically loaded subintervals can be treated the same as underloaded subintervals. However, unlike an overloaded interval, we cannot conclude that we necessarily have T 2>t 2 for an underloaded interval. Moreover, even if T 2>t 2 for each underloaded interval, we could have infinitely many switches in a finite interval. We directly assume that those pathological situations do not occur.
Assumption 7
(Finitely many switches between intervals in finite time)
Each underloaded interval is of positive length, so that the positive half line [0,∞) can be partitioned into overloaded and underloaded intervals. Moreover, there are only finitely many switches between overloaded and underloaded intervals in each finite interval.
For engineering applications, Assumption 7 is reasonable, but it is unappealing mathematically. We would like to have natural conditions on the model parameters under which the conclusion does hold. For the special case of M service and for the extension to time-varying Markovian service (M t ), we provide sufficient conditions for Assumption 7 to be satisfied in [20]. From a practical perspective, Assumption 7 provides no restriction, because we can discover violations when calculating the performance descriptions, and remove any violation that we discover by negligibly modifying either the arrival-rate function λ or the staffing function s in a neighborhood of the problem time t to remove the problem. That is most easily done with the arrival-rate function λ, because we only require that it be piecewise-continuous. For t in a short interval [a,b], we can replace λ(t) by λ(t)±ϵ. This will introduce new discontinuity points at the end points a and b (if they were not already discontinuity points), but that leaves λ∈ℂ p .
All assumptions above are in force throughout this paper. We will introduce additional regularity assumptions as needed, starting in Sect. 6. We now determine the performance, first considering an underloaded interval.
4 Scale proportionality
To treat an underloaded interval in the next section, we will exploit an important scale-proportionality property of the M t /GI/∞ stochastic queueing model; see Remark 5 of [10]. For each c>0, let B c (t,y) be the number of customers in service in the M t /GI/∞ stochastic model at time t that have been so for a duration at most y when the system starts empty at time 0 and the arrival-rate function is λ c (t)≡cλ(t), for some given arrival-rate function λ and service cdf. The following is proved like Theorem 1 of [10], using the two-parameter framework, as in [31].
Proposition 1
(Scale proportionality in the M t /GI/∞ stochastic model)
For all c>0, B c (t,y) has a Poisson distribution with mean
As a consequence of the SLLN for the Poisson distribution, we see that c −1 B c (t,y)→m 1(t,y) as c→∞ for each t and y. In addition, we have the more general FWLLN in [31, 33], which implies that c −1 B c (t,y)→m 1(t,y), regarded as functions of t and y. Hence, the mean function m 1(t,y) in the M t /GI/∞ stochastic queueing model directly coincides with the limit of the scaled process; i.e.,
where B(t,y) is the fluid content in service at time t that have been so for a duration at most y in the M t /GI/∞ fluid model. Thus, aside from scale, the mean m c (t,y)≡E[B c (t,y)] in the M t /GI/∞ stochastic model coincides with the corresponding fluid content in the deterministic fluid model.
Moreover, the conclusions above extend to the more general G t /GI/∞ models. First, the mean function in (12) above in the G t /GI/∞ stochastic model actually coincides with the mean function in the M t /GI/∞ stochastic model, provided that the arrival-rate function is the same; this observation is made in Remark 2.3 of [26]. Second, the FWLLN in [31, 33] actually holds for the G t /GI/∞ stochastic model, provided that the arrival process satisfies a FWLLN. To summarize, the mean function in the M t /GI/∞ stochastic model coincides with the fluid content in the corresponding G t /GI/∞ fluid model, assuming appropriate scale.
This scale proportionality in the infinite-server stochastic model actually extends to the more general G t /GI/s t +GI fluid model. The following scale-proportionality result is a consequence of the results in this paper.
Theorem 1
(Scale proportionality in the G t /GI/s t +GI fluid model)
If the vector (b c (t,x),q c (t,x),w c (t),v c (t),α c (t),σ c (t)) is the performance at time t associated with model data (cλ,cs,F,G,cb(0,⋅),cq(0,⋅)), then
5 An underloaded interval
We will consider the system over successive intervals, during each of which it is either underloaded or overloaded, as defined in Sect. 3. We start with the easier case, in which the system is underloaded. Without loss of generality, we assume that an underloaded interval starts at time 0 and terminates at a time T, defined in (11). We do not need to know in advance the termination time T. Instead, we can assume that the system is underloaded over the full interval [0,∞) and then calculate T.
If the G t /GI/s t +GI fluid model is underloaded, then there is no queue, and so no abandonment. Then the model is equivalent to the associated G t /GI/∞ fluid model.
Proposition 2
(Service content in an underloaded interval)
For the fluid model with unlimited service capacity (s(t)≡∞ for all t≥0), the integral representation in (2) is valid for B and b, with

If, instead, a finite-capacity system starts underloaded, then the same formulas apply over the interval [0,T), where the underload termination time is T≡inf{t≥0:B(t)>s(t)}, with T=∞ if the infimum is never obtained. Hence, b(t,⋅),b(⋅,x)∈ℂ p for all t≥0 and x≥0, for t in the underloaded interval.
Proof
The first term in the expression for B(t,y) in (13) represents the content due to new input; it follows from Sect. 4. The second term represents the content to old content still in service; it follows from Assumption 6, along with Assumption 2. It is evident that, for each t, B(t,y) is differentiable in y for all y except y=t. Thus, for each t≥0, B(t,y) is absolutely continuous as a function of y and has the density b(t,x) displayed above. In addition, by Assumption 2, b(t,⋅),b(⋅,x)∈ℂ p for all t≥0 and x≥0. □
During an underloaded interval, b(t,x) depends upon the pair (λ,G) and the initial condition b(0,x). There is no queue, so (q,F,w,v) play no role. The different roles of the two regimes are summarized in Fig. 4. Hence, Proposition 2 fully describes the performance during underloaded intervals. The final piecewise-continuity conclusion ensures that the piecewise-continuity property assumed for b(0,⋅) will pass on to subsequent intervals when we consider successive intervals.
Remark 1
(Discontinuity at t=x)
From (13), we see that b inherits the smoothness of G, λ and q(0,⋅) except when t=x. That will be a persistent theme throughout our analysis. For general initial conditions, this discontinuity is fundamental, so we cannot expect greater smoothness. However, away from the set {(t,x):t=x}, we can expect smoothness of the model parameters to be reflected in our performance descriptions.
Remark 2
(The generic scalar transport PDE)
If, in addition to the assumptions of Proposition 2, λ and b(0,⋅) are differentiable a.e. with respect to Lebesgue measure on [0,∞), then, for each t and x, b(t,x) has first partial derivatives with respect to t and x a.e. with respect to Lebesgue measure on [0,∞). Moreover, b satisfies the following PDE a.e. with respect to Lebesgue measure on [0,∞)×[0,∞), a simple version of the generic scalar transport equation:
with boundary conditions {b(t,0)=λ(t):t≥0} and {b(0,x):x≥0}; see [24].
We now give a monotonicity result comparing two underloaded fluid models. For this result, we exploit hazard-rate order, writing \(h_{G_{1}} \le h_{G_{2}}\) if \(h_{G_{1}} (x) \le h_{G_{2}} (x)\) for all x≥0, for cdf’s satisfying the assumptions in Sect. 3. It is easy to see that hazard-rate order implies ordinary stochastic order via the representation
Proposition 3
(Comparison result for b in an underloaded model)
Consider two underloaded fluid models. If λ 1≤λ 2, b 1(0,⋅)≤b 2(0,⋅) and \(h_{G_{1}} \ge h_{G_{2}}\) as functions, then b 1≤b 2, i.e., b 1(t,x)≤b 2(t,x) for all t≥0 and x≥0, and T 1≤T 2, where T i is the underload termination time in model i.
Proof
Apply (13) after applying (14) to write
□
The system could be in an underloaded period for an extended period of time. If so, it is often convenient to consider the system starting empty in the distant past. (That is done for the corresponding infinite-server queueing models in [10, 26].) That allows us to directly construct stationary versions, including periodic versions, if that is warranted.
Proposition 4
(Starting empty in the distant past)
Suppose the system started empty in the distant past (at t=−∞) and has been underloaded up to time t. If \(\int_{0}^{\infty} \bar{G} (x)\lambda(t-x) \, dx, < \infty\), then

for x≥0 and y≥0. If the arrival-rate function λ is constant or periodic, then so are b(t,⋅), B(t) and B(t,⋅).
As noted above, the expression for B(t) coincides with the mean number of busy servers in the M t /GI/∞ model studied in [10, 26]; see these sources for additional structural results. The expressions for the two-parameter function B(t,y) and b(t,x) coincide with the corresponding mean values in [31].
6 The service content density in an overloaded interval
Without loss of generality, we assume that the overloaded interval begins at time 0 and ends at time T satisfying (10). Again, we do not need to know the end time T in advance, because we can calculate it while we are calculating the performance measures q and w. We proceed under the assumption that the arrival rate is sufficiently large that the system is overloaded throughout a specified interval [0,T) (up to, but not including, time T), and afterwards detect violations before time T, if there are any, and then reduce the interval, if necessary.
6.1 The special case of M service
The service content density is easy to compute if the service distribution is exponential, so we consider that case first. From (5), we can write down an expression for b(t,x) during the overloaded interval:

where b(0,x−t) is part of the initial conditions, but where b(t−x,0) remains to be specified.
Since the service is exponential, the output rate, σ(t), and thus the rate fluid enters service, b(t,0), depend only on the staffing function s, in particular, on the values s(t) and s′(t). (Recall that the mean service time has been fixed at 1.)
Proposition 5
(The service content in an overloaded interval)
The departure (service completion) rate satisfies σ(t)=B(t), t≥0, and, during each overloaded interval, the departure rate σ(t) and rate fluid enters service b(t,0) have the simple form
depending only on the staffing function s. Then b is fully characterized by (15) and (16) during an overloaded interval. Also b(t,⋅),b(⋅,x)∈ℂ p for all x, t<T.
Proof
Apply (9). □
6.2 General GI service
We start with the general expression for the service content density given in (15), but it requires the rate into service b(t,0), which is part of what we are trying to determine. Since the system is assumed to be overloaded over an initial interval [0,T), the rate into service is determined by the rate service capacity becomes available. Thus, by (9), we have
We now substitute (15) into (17) to obtain the following equation for the function b(t,0):
where
From (19), we see that \(\hat{a} \in \mathbb {C}_{p} \subseteq \mathbb {D}\) provided that the integral in (19) is finite. That will hold under regularity conditions, as we will explain below.
We now specify two ways to show that the fixed-point (18) has a unique solution and how it can be numerically calculated. First, we can recognize that (18) is a renewal equation, as in Sect. V.2 of [4]. Thus, the existence of a unique solution to (18) follows from Theorem 2.4 on p. 146 of [4]. However, computation of the solution by this approach seems not elementary. One possible way is to apply Laplace transforms. From (18), we obtain the following equation for the associated Laplace transforms (replacing the variable t by s):
which has explicit solution
Given the transforms \(\mathcal {L}(\hat{a}) (s)\) and \(\mathcal {L}(g) (s)\), the numerical values of the function b(t,0) can be effectively computed by numerical transform inversion, e.g., using the Fourier-series method in [1, 2]; see especially Sect. 13 of [1]. However, this requires computation of the transforms \(\mathcal {L}(\hat{a})(s)\) and \(\mathcal {L}(g) (s)\) for the required arguments s. Since only a few arguments s are required, this approach is feasible, but somewhat cumbersome.
We now present an alternative way to show that (18) has a unique solution and numerically calculate that solution. From (18), it is evident that b(t,0) is a fixed point of the operator \(\mathcal {T}: \mathbb {D}\rightarrow \mathbb {D}\), where
Under regularity conditions, we can show that there exists a unique solution to (18) by applying the Banach (contraction) fixed-point theorem. We will use the complete (nonseparable) normed space \(\mathbb {D}\) with the uniform norm over the interval [0,T], i.e.,
The proof of completeness follows the same argument used for the space ℂ; see pp. 150, 220 of [6].
We will require an additional bound on the tail of the initial service content density b(0,⋅). Recall that we have assumed that \(\bar{G} (x) > 0\) for all x.
Assumption 8
(Tail of b(0,⋅))
The tail of b(0,⋅) is bounded relative to the service-time pdf g via
Assumption 8 warrants discussion, because it is unappealing. At first glance, it passes the requirement that the assumptions be on the model data, because the service density g, the associated cdf G and the initial fluid content in service b(0,⋅) are all part of the model data. However, in application we will be applying the algorithm recursively over several UL and OL intervals. We would thus not know in advance the function b(0,⋅) in all OL intervals after an initial one. It is thus important that we provide readily available sufficient conditions for Assumption 8 to hold; we do that after we state the theorem. For now, we point out that there is a simple practical condition implying Assumption 8 to hold: It suffices for the service hazard-rate function h G to be bounded. (See below.)
Theorem 2
(Service content in the overloaded case)
Consider an overloaded interval [0,T]. If Assumption 8 holds, then the operator \(\mathcal {T}\) in (22) is a monotone contraction operator on \(\mathbb {D}\) with contraction modulus G(T) for the norm ∥⋅∥ T defined in (23), so that a finite function b(t,0) is uniquely characterized via equation (18). Hence, for any \(u \in \mathbb {D}\), the fixed point can be approximated by the n-fold iteration \(\mathcal {T}^{(n)}\) of the operator \(\mathcal {T}\) applied to u, with
and, if \(u \le(\ge)\mathcal {T}(u)\), then \(\mathcal {T}^{(n-1)} (u) \le(\ge) \mathcal {T}^{(n)} (u) \le(\ge) \hat{b}\) for all n≥1.
Proof
Clearly, Assumption 8 implies that \(\|\hat{a} \|_{T} < \infty\), so that \(\mathcal {T}\) maps \(\mathbb {D}\) into \(\mathbb {D}\). Moreover, the contraction property follows from

□
Remark 3
(Weakening the condition on G)
Note that we require G(T)<1 in the proof of Theorem 2, which holds because we have assumed that \(\bar{G}(x) >0\) for all x. However, that requirement is actually not necessary, because we can always work in an interval [0,δ] as long as G(δ)<1 for some δ>0. We can show the uniqueness of b(⋅,0) for all 0≤t≤T by recursively considering successive intervals of length δ.
We can deduce from Theorem 2 that an analog of Proposition 2 holds in OL intervals.
Corollary 1
(The integral representation (2) in an OL interval)
The integral representation in (2) is valid in OL intervals as well as in UL intervals.
We now return to Assumption 8, which restricts the class of allowed service cdf’s in a rather complicated way. We will show that it suffices for the service hazard rate h G to be bounded. But even that is often not necessary in practice. It is important to note that Assumption 8 is always satisfied in a case of principal interest: if there exists y 0 such that b(0,y)=0 for all y≥y 0. That case occurs whenever the system started empty at some (finite) time in the past. That case occurs if the overloaded interval of interest begins at time t, 0≤t<T, after the system has begun empty with b(0,y)≡0 for all y; then necessarily b(t,y)=0 for all y>t, by virtue of Assumption 6. Then
where x ↑(t)≡sup{x(s):0≤s≤t}.
Nevertheless, other initial conditions are interesting. For example, for the stationary model, we might start with the stationary fluid content, which has the form we have \(b(0,y) = \bar{G}(y)\), y≥0, because \(\bar{G}\) is the stationary-excess or equilibrium-residual-lifetime density of the service-time distribution; see [37]. Thus we now present other sufficient conditions for Assumption 8.
Remark 4
(Sufficient conditions for the bound when B(t)−B(0,y)>0 for all y)
Clearly, we need to control the initial content density b(0,y) and/or the service pdf g(y) in order for Assumption 8 to hold. An easy sufficient condition directly related to the stationary fluid content density for the stationary model is that there exist a constant K such that \(b(0,y) \le K\bar{G} (y)\) for all y≥0. Another easy sufficient condition for the bound in Assumption 8 is that we should have
In turn, three different sufficient conditions for (26) are:
-
(i)
$$\sup_{x \ge0}{\bigl\{h_G (x)\bigr\}} < \infty\quad\bigl(\mbox{bounded hazard rate, using } B(0) < \infty\bigr);$$
-
(ii)
there exist β>0 and K such that
$$\int_{0}^{\infty} b(0,y) e^{\beta y} \, dy <\infty\quad \mbox{and}\quad h_G(x) \le K e^\beta x \quad \mbox{for all } x\ge0;$$ -
(iii)

So far, we can only conclude that the function \(b(t,0) \in \mathbb {D}\). We can obtain additional smoothness properties by imposing additional smoothness conditions on the model elements s and g. We use these properties for b(⋅,0) to establish properties of the ODE to calculate the BWT w in Sect. 4 of [20].
Corollary 2
(Smoothness of service content in the overloaded case)
If s′ and g are continuous, then b(⋅,0) is continuous as well. In that case, b(⋅,x) and b(t,x) are elements of ℂ p for each x≥0 and t≥0.
Proof
Under the extra smoothness conditions, we can apply the contraction fixed-point theorem on the closed subspace ℂ of continuous functions in \(\mathbb {D}\), with the same uniform norm. Then the fixed point b(t,0) is necessarily in ℂ as well, from which we deduce that b(⋅,x) and b(t,x) are elements of ℂ p for each x≥0 and t≥0. □
We discuss alternative algorithms to calculate b in Appendix C in [24].
7 The queue performance functions
We now turn to the queue during an overload interval. To do so, it is convenient to initially ignore the flow into service.
7.1 The queue content ignoring flow into service
Let \(\tilde{q} (t,x)\) be q(t,x) during the overload interval [0,T) under the assumption that no fluid enters service from queue. We can once again invoke the connection to the M t /GI/∞ stochastic model, discussed in Sect. 4 to treat \(\tilde{q} (t,x)\) just as we treated b in Sect. 5, because we can let the general patience cdf F play the role of the general service-time cdf G. Instead of (5), we can write
to obtain the following proposition. The proof is just like the proof of Proposition 2 for B.
Proposition 6
(Queue content without transfer into service in the overloaded case)
In the overloaded case, the integral representation in (2) is valid for \(\tilde{Q}\) and \(\tilde{q}\), with

Remark 5
Just as we observed for b in an underloaded interval in Remark 2, in an overloaded interval \(\tilde{q}\) satisfies a version of the generic scalar transport PDE.
Paralleling Proposition 3, we have the following comparison result, proved in the same way.
Proposition 7
(Comparison result for \(\tilde{q}\))
Consider two overloaded fluid models. If λ 1≤λ 2, q 1(0,⋅)≤q 2(0,⋅) and \(h_{F_{1}} \ge h_{F_{2}}\) as functions, then \(\tilde{q}_{1} \le\tilde{q}_{2}\), i.e., \(\tilde{q}_{1} (t, x) \le \tilde{q}_{2} (t,x)\) for all t≥0 and x≥0.
We now derive q and w. The proper definition and characterization of the BWT w is somewhat complicated. We easily get an expression for q provided that we can find w.
Corollary 3
(From \(\tilde{q}\) to q)
Given the BWT w,

Moreover, q(t,⋅)∈ℂ p for all t≥0.
Proof
Combine Proposition 6 and (29) to deduce that q(t,⋅)∈ℂ p for all t, x. □
7.2 The boundary waiting time w
It now remains to define and characterize the BWT w. We can define the BWT w by exploiting flow conservation, in particular, by exploiting the fact that two expressions for the amount of fluid to enter service over any interval [t,t+δ] coincide; i.e.,
where
is the amount of fluid removed from the right boundary of \(\tilde{q}\), starting at x=w(t)−ϵ(t,δ) and ending at x=w(t), during the time interval [t,t+δ] (where ϵ(t,δ) is yet to be determined) and A(t,t+δ) is the amount of the fluid content in I that abandons in the interval [t,t+δ]. We define the BWT w by letting δ↓0 in (30). We will show in Theorem 3 below that, under regularity conditions, the relation in (30) determines an ODE for w that has a unique solution. Hence, we will show that the relation (30) serves to properly define w and characterize it.
We need two more regularity conditions. First, we assume that the initial value w(0) for the interval we consider is finite. We will be representing w as the solution of an initial value problem involving an ODE, so this is needed.
Assumption 9
(Finite initial BWT)
0≤w(0)<∞.
Second, we require that the functions λ(t) and q(0,x) be appropriately bounded away from 0.
Assumption 10
(Positive arrival rate and initial queue density)
For all t≥0,

By (28) for \(\tilde{q}\), Assumption 10 for λ implies that \(\tilde{q} (t, x) > \epsilon\bar{F} (x) > 0\) on [0,T) for some positive ϵ. That is useful because \(\tilde{q} (t, x)\) appears in the denominator in an expression for the derivative of w in (32) below. The BWT w can be discontinuous if these functions are 0 over subintervals; we give examples in Appendix E of [24]. We show that w can be discontinuous if λ(t)=0 or q(0,⋅)=0 over a subinterval, while w can have an infinite derivative corresponding to zeros of these functions. However, we obtain the following positive result, proved in Sect. 11. Let x(t+) and x(t−) denote the right and left limits of a function x at t, respectively. We can obtain a more elementary statement and proof if we assume even more regularity conditions; see Appendix D in [24].
Theorem 3
(The BWT ODE)
Consider an overloaded interval [0,T). If Assumptions 9–10 hold, then the BWT w is well defined being the unique solution of the initial value problem (IVP) on [0,T) based on the ODE
and any initial value w(0). In addition, w is Lipschitz continuous on [0,T] with w(t+u)≤w(t)+u for all t≥0 and u≥0 with t+u≤T. Moreover, w is right differentiable everywhere with right derivative w′(t+) given in (32) and left differentiable everywhere (but not necessarily differentiable) with value

Overall, w is continuously differentiable everywhere except for finitely many t.
Remark 6
(Different roles of b(t,0) and F in shaping q)
Our use of \(\tilde{q}\) as an intermediate step in constructing q helps show the different roles played by b(t,0) and F in producing q. First, the abandonment (F) controls the shape of \(\tilde{q}(t,x)\) and thus q(t,x) only for x<w(t). Second, the transportation rate b(t,0) controls only w(t), the right boundary or the truncation of \(\tilde{q}(t,x)\) on x; it does not affect \(\tilde{q}(t,x)\) itself, and thus q(t,x) for any 0≤x<w(t).
We give closed-form formulas for some special cases in the next corollary, proved in Appendix D of [24].
Corollary 4
Suppose the system is overloaded for 0≤t<T and w(0)=0.
-
(a)
For the G t /M/s t fluid model without customer abandonment (\(\bar{F}(x)=1\) for x≥0),

for Λ −1(x)≡inf{y>0:Λ(y)=x}, and \(\bar{t} \equiv \inf\{t>0:\varLambda (t)=\int_{0}^{t}b(y,0)\,dy\}\).
-
(b)
For the G t /M/s t +M fluid model, where the abandonment-time cdf is exponential \((\bar{F}(x)=e^{-\theta x}\), x≥0),
 (34)
(34)where \(\tilde{\varLambda }(t)\equiv\int_{0}^{t}\lambda(y)e^{\theta y}\,dy\), \(\tilde{\varLambda }^{-1}(x)\equiv\inf\{y>0:\tilde{\varLambda }(y)=x\}\), and \(\tilde{t}\equiv \inf\{t>0:\tilde{\varLambda }(t)=\int_{t_{1}}^{t}b(y,0)e^{\theta y}\,dy\}\).
We conclude this section by combining Proposition 6, Corollary 3 and Theorem 3 to deduce that the integral representation in (2) is valid for Q as well as B and \(\tilde{Q}\).
Corollary 5
(Integral representation for Q)
In the overloaded case, the integral representation in (2) is valid for Q and q, with w in Theorem 3 and q in Corollary 3.
7.3 The potential waiting time
In the previous subsection, we characterized the dynamics of the BWT w. Now we want to connect w to the PWT v, the waiting time of an arriving quantum of fluid at time t that is infinitely patient.
As shown in [29], the PWT v can be defined as a first passage time, with abandonment after time t computed with the input turned off; also see [34]. Let A t (u) be the total fluid abandoning in the interval [t,t+u] in our fluid model, modified by having the input shut off after time t. Paralleling (7),
where α t (s) is the abandonment rate of the fluid that arrives before time t, at time s.
With (35), we can define v(t) as
where E(t) is the amount of fluid to enter service in the interval [0,t], as in (8), i.e., \(E(t) \equiv\int_{0}^{t} b(u,0) \, du\), t≥0. However, in general, so far, we have not assumed enough to guarantee that the PWT v is finite. It is possible for fluid to arrive and never be served; we need to rule that out.
First, we show that any initial fluid content in the system eventually must leave. Let B 0(t) be the portion of the initial fluid content in service, B(0), that is still in service at time t; let Q 0(t) be the portion of the initial fluid content in queue, Q(0), that is still in queue at time t.
Proposition 8
(Dissipation of initial fluid content)
For t≥0,

Proof
The representation is immediate. It is elementary that B 0(t)≤B(0) and \(\tilde{Q}_{0} (t) \le\tilde{Q}(0) = Q(0)\). By Assumption 1, B(0)<∞ and Q(0)<∞. The convergence then follows from the Lebesgue dominated convergence theorem. □
However, the queue will not dissipate in finite time by abandonment alone, because \(\bar{F} (x) > 0\) for all x≥0. Hence we need to have fluid enter service from the queue. Even if we invoke Assumption 9, and have w(0)<∞, so that we have w(t)≤w(0)+t<∞ for all t≥0, we cannot guarantee that v(0)<∞. Indeed, we would have v(t)=∞ for all t≥0 if no fluid from queue were ever admitted into service. That in turn would be the case if we used the feasible staffing function s(t)≡B 0(t), which is positive for all t when B(0)>0, because \(\bar{G} (x) >0\) for all x≥0. In order to avoid such problems, we introduce two more regularity conditions:
Assumption 11
(Minimum staffing level)
There exists a constant s L such that s(t)≥s L >0 for all t≥0.
Assumption 12
(Minimum service hazard rate)] There exists a constant h G,L such that h G (x)≥h G,L >0 for all x≥0.
Theorem 4
(Finite PWT)
Under Assumptions 11 and 12, the rate of service completion is bounded below: σ(t)≥s L h G,L for all t≥0. As a consequence,
We give the proof in Appendix D of [24]. Given that the PWT v is indeed bounded above as in Theorem 4, we can obtain it from our algorithm for w. The idea is simple: If, at time t, the elapsed waiting time of the quantum of fluid that is entering service is w(t), then this quantum of fluid arrived in queue w(t) units of time ago. That implies that the PWT at t−w(t) is w(t). We prove the following in Sect. 11.
Theorem 5
(The PWT v and the BWT w)
Consider an overloaded interval with Assumptions 9–10 holding and w(0)=0. If v(t)<∞ for all t≥0 (for which Assumption 11 is a sufficient condition, by Theorem 4), then v is the unique function in \(\mathbb {D}\) satisfying the equation
as depicted in Fig. 5. Moreover, v is discontinuous at t if and only if there exists ϵ>0 such that w(t+v(t)+ϵ)=w(t+v(t))+ϵ, which in turn holds if and only if b(u,0)=0 for t+v(t)≤u≤t+v(t)+ϵ. If b(⋅,0)>0 a.e. with respect to Lebesgue measure, then v is continuous.
The proof of Theorem 5 directly gives an algorithm to compute the PWT v given the BWT w. Similarly, the second equation in (37) can provide an algorithm to construct w given v. We now provide an alternative characterization of v via its own ODE, but this alternative characterization involves an extra condition. We give the proof in Sect. 11.
Theorem 6
(Right derivative and ODE for v)
Under the conditions in Theorem 5, the right derivative of v always exists (except possibly infinite), with value

The right derivative at t is finite if and only if b(t+v(t),0)>0. If t is a continuity point of v, then the left derivative exists as well, with
If Φ is continuous at t, then v is differentiable at t, and v satisfies the first ODE. If, in addition, b(t,0)>0 for all t, then v is continuous. Then v is differentiable except at only finitely many t, and there exists a unique solution to the first ODE.
Remark 7
(Algorithm for v and w)
In an algorithm, it is convenient to avoid the complications for w and v that occur when b(t,0)=0. To do so, we can introduce an ϵ-approximation, letting b ϵ (t,0)≡b(t,0)+ϵ, 0≤t≤T, only to be used in the calculation of w and v. Let w ϵ be w and v ϵ be v with b(t,0) replaced by b ϵ (t,0). Since \(w' \ge w_{\epsilon}'\) and \(v' \ge v_{\epsilon}'\), we have w ϵ ↑w and v ϵ ↑v as ϵ↓0.
We could also enforce a lower bound for b(t,0) directly in our model by imposing a constraint on our staffing. We could require that b(t,0)≥b ∗>0 for all t in order for the staffing function s to be feasible. Since b(t,0)=s′(t)+σ(t), that translates into the staffing constraint
In Appendix D of [24] we give closed-form formulas for the PWT v in some special cases, paralleling those for the BWT w given in Corollary 4.
8 Overview of the total algorithm
We now summarize the full algorithm for the G t /GI/s t +GI fluid model. We alternately consider successive underloaded and overloaded intervals (under the assumption that any finite interval can be partitioned into finitely many of these, which can be verified in the computation). For each underloaded interval, we start with initial conditions as indicated in Sect. 3. We can compute the single key performance measure b directly by applying Proposition 2. We then end the underloaded interval the first time B(t) exceeds s(t). Since the queue is empty, the functions q, w and v do not appear.
8.1 An overloaded interval with M service
An overloaded interval is more complicated. There are two cases: (i) M service and (ii) non-M GI service. For M service, we do not need to solve the fixed-point equation (18) for the rate fluid enters service from the queue, b(t,0). With M service (at rate 1), we know that b(t,0)=s′(t)+s(t), by Proposition 5. The algorithm starts with initial conditions as in Sect. 3. The algorithm begins by calculating \(\tilde{q}\) via Proposition 6 and b and b(t,0) via Proposition 5. We then calculate w by solving the ODE (32) and then the function v (37), as explained in the proof of Theorem 5. We consider terminating the overloaded interval the first time that w(t)=0. At that time we check to see if the interval actually remains overloaded, by looking at the net flow rate into the queue r(t)≡λ(t)−s′(t)−σ(t) (see (10)). If r(t)>0, then we continue the overloaded interval. Otherwise, we shift to the next underloaded interval. We present additional details about the algorithm for M service in Appendix G of [24].
8.2 An overloaded interval with GI service
With non-M service, we need to solve the fixed-point equation (18) for the rate fluid enters service from the queue, b(t,0), in addition to the other steps with M service. We now formally state the algorithm to compute all performance functions in an overloaded interval of the G t /GI/s t +GI fluid model. Consider an interval [0,T] and assume that the system is overloaded at t=0, i.e., Q(0)>0 and B(0)=s(0). However, we typically do not know when the overloaded interval ends in advance. The objective is to determine the overload termination time T 1 defined in (10) with t 1=0 along with the other performance functions. Hence, we determine q(t,⋅) and b(t,⋅) for 0≤t≤T∧T 1. If T 1<T, the system simply switches to an underloaded interval; otherwise, the system stays overloaded in [0,T].
The input functions are the model parameters F, G, λ(t) and s(t) for 0≤t≤T and initial condition q(0,⋅), b(0,⋅) and w(0). We require that these conditions satisfy (i) \(s(0)=B(0)=\int_{0}^{\infty}b(0,y)\,dy\) and (ii) \(Q(0)=\int_{0}^{w(0)}q(0,y)\,dy>0\). Applying the fixed-point operator discussed in Sect. 6, we have the following algorithm:
-
1.
u (0)(t)←0, \(a(t)\leftarrow s'(t) +\int_{0}^{\infty}b(0,y)\frac{g(t+y)}{\bar{G}(y)}\,dy\), i←1
-
2.
\(u^{(i)}(t)\leftarrow a(t) + \int_{0}^{t}u^{(i-1)}(y)g(t-y)\,dy\) for 0≤t≤T
-
3.
If ∥u (i)−u (i−1)∥ T >ϵ, then i←i+1 and go to Step 2; otherwise b(t,0)←u (i)(t) for 0≤t≤T
-
4.
Solve the BWT ODE and determine T 1
-
5.
Compute b(t,x) using (15) for 0≤t≤T∧T 1. End
Note that ϵ is the (small positive) error threshold level that we specify in advance. Here we let the contraction iteration in Step 2 end when the uniform distance between the u functions in two consecutive iterations is small.
The algorithm above requires that the given staffing function s be feasible. However, we can also easily modify the algorithm so that infeasibility can be detected. That extension is discussed in Appendix G of [24]. With the algorithm above, we will see that s is infeasible (if it is) in Step 4 by observing that b(t,0)≤0 for some 0≤t≤T; see the next section.
9 Feasibility of the staffing function
So far, we have assumed that the staffing function s is feasible, yielding
for all t≥0 such that B(t)=s(t). This requirement is automatically satisfied in underloaded intervals when B(t)=s(t), because in that case we require that s′(t)+σ(t)≥λ(t) where necessarily λ(t)≥0. Feasibility is only a concern during overloaded intervals, and then only when the staffing function is decreasing, i.e., when s′(t)<0.
The first violation is easy to detect: Let t ∗ be the time of first violation. Let I n be the nth overloaded subinterval in [0,∞) determined under the assumption that the original staffing function s is feasible. Let I be the union of these subintervals, i.e., the subset of [0,∞) during which the system is overloaded. Then
Even though we require (39), so far we have done nothing to prevent having t ∗<∞ (violation). Thus, we compute b and detect the first violation.
Correcting the staffing function is not difficult either (by which we mean replacing it with a higher feasible staffing function): We simply construct a new staffing function s ∗ consistent with turning off the input into the queue (setting b(t,0)=0) starting at time t ∗ and lasting until the first time t after t ∗ at which s ∗(t)=s(t). (By the adjustment, we will have made s ∗(t ∗+)>s(t ∗+).) Since the system has operated differently during the time interval [t ∗,t], we must recalculate all the performance measures after time t, but we have now determined a feasible staffing function up to time t>t ∗. By successive applications of this correction method (adjusting the staffing function s and recalculating b), we can construct the minimum feasible staffing function overall.
To make this precise, let \(\mathcal {S}_{f,s} (t)\) be the set of all feasible staffing functions for the system over the time interval [0,t], t>t ∗, that coincide with s over [0,t ∗]; i.e., with \(\mathbb {C}^{2}_{p} (t)\) denoting the set of twice differentiable positive real-valued functions on [0,t] with second derivatives in ℂ p , let

for t ∗ in (40), where \(b_{\tilde{s}}\) is the function b associated with the model with staffing function \(\tilde{s}\).
Theorem 7
(Minimum feasible staffing function)
Assume that \(s \in \mathbb {C}^{2}_{p}\) and \(b_{\tilde{s}}(\cdot,0)\) exists and is continuous for each \(\tilde{s} \in \mathcal {S}_{f,s} (t))\). Then there exist δ>0 and \(s^{*} \in \mathcal {S}_{f,s} (t^{*}+ \delta)\) in (41) for t ∗ in (40) such that
i.e., \(s^{*} \in \mathcal {S}_{f,s} (t^{*} + \delta)\) and \(s^{*} (u) \le\tilde{s}(u)\), 0≤u≤t ∗+δ, for all \(\tilde{s} \in \mathcal {S}_{f,s}(t^{*}+ \delta)\). In particular,
Moreover, δ can be chosen so that
with δ≡∞ if the infimum in (44) is not attained.
Proof
First, since b s (⋅,0) is continuous for our original s, the violation in (40) must persist for a positive interval after t ∗; that ensures that a strictly positive δ can be found.
We shall prove that \(\tilde{s}\geq s^{*}\) over [t ∗,t ∗+δ] for s ∗ in (43) and any feasible function \(\tilde{s}\), and we will show that s ∗ itself is feasible. For 0≤t≤t ∗+δ, suppose \(\tilde{s}\) is feasible. Since the system is overloaded, system being in the overloaded regime implies that

where equality on the second line holds because of the fundamental evolution equations in Assumption 6 and because \(b_{\tilde{s}} (t^{*}, x) = b_{s} (t^{*}, x)\) for all x, and the inequality holds because \(b_{\tilde{s}}\geq0\). On the other hand, the equality holds when \(b_{\tilde{s}}(t^{*} + u,0)=0\) for all u, which yields B(t ∗+u)=s ∗(t+u). Therefore, the proof is complete. □
Corollary 6
(Minimum feasible staffing with exponential service times)
For the special case of exponential service times, i.e., with \(\bar{G}(x) \equiv e^{-x}\), (43) becomes simply s ∗(t ∗+u)=B(t ∗)e −u, 0≤u≤δ.
We have constructed a minimal feasible staffing function by requiring that the new staffing function agree with the original one up until the time of the first violation. We have shown that assumption leads to a unique minimum feasible staffing function. However, it may be desirable to consider other approaches to feasibility, where we have the freedom to revise the staffing function before t ∗ as well as afterwards. It is natural to frame the issue as an optimization problem; e.g., as in productions smoothing, we might want to impose costs for fluctuations of the staffing function as well high values. We leave such investigations for future work.
10 Staffing the G t /GI/s t +GI fluid model to stabilize delays
So far, we have discussed the performance analysis of the G t /GI/s t +GI fluid model with the staffing function s regarded as a given function. In this section, we assume that we are free to choose the staffing function s, and do so with the objective of stabilizing the potential waiting time v at some (constant) target v ∗>0. This delay stabilization problem is a variant of one considered previously for many-server queueing models with time-varying arrival rates in [12]. In [12], the goal was to stabilize the probability an arrival experiences any delay. in contrast, here we stabilize the delay of all fluid at precisely v ∗>0. Now everybody must wait, but only v ∗.
As a consequence of Theorem 5, we see that, in order to stabilize v at v ∗, it suffices to stabilize w at v ∗. By Theorem 3, we see that we will be able to do so if and only if we can find a staffing functions s for which the resulting performance satisfies the equation
which implies that we must have b(t,0)=q(t,v ∗) when w(t)=v ∗.
Suppose that the system is initially empty, i.e., b(0,x)=q(0,x)=0 for all x>0. Thus, we do not start staffing the service facility until time v ∗, so that no input enters service during [0,v ∗]; i.e., we let b(t,0)=0 for 0≤t≤v ∗, in order to let w increase from 0 to v ∗. At time v ∗, the input at time 0 is sent to the queue, after waiting precisely time v ∗.
With the initial conditions q(t,0)=λ(t) and q(0,x)=0, the queue instantly becomes overloaded at time 0, and we can apply Proposition 6 and Corollary 3 (or (5)) to obtain
Combining (45) and (46), we obtain the transportation rate after t=v ∗:

With the explicit expression of b(t,0) and b(0,x)≡0, x≥0, (5) implies that
Therefore, we can easily compute B(t), σ(t), q(t,x), Q(t) and α(t) for t>v ∗. We have just proved the following theorem.
Theorem 8
Consider the G t /GI/s t +GI fluid model with a general arrival-rate function λ. Suppose the system is initially empty. For any specified constant v ∗>0, we can make the system overloaded such that the PWT is fixed at v ∗, i.e., v(t)=v ∗ for all t≥0, by
-
(i)
not allowing any input to enter service until time t=v ∗,
-
(ii)
letting the service-capacity function be
 (48)
(48) -
(iii)
operating the queue in the usual FCFS manner after time v ∗ with b(t,0)>0. If we do so, then w(t)=v ∗ for t≥v ∗ and w(t)=t for t≤v ∗,

If λ is a periodic function, then so are b(⋅,x), B(⋅)=s ∗(⋅), σ, q(⋅,x), Q(⋅) and α after time v ∗, with the same period.
Remark 8
(Connection to the QED regime when v ∗=0)
All the analysis in this section can be extended to the delay target v ∗=0. In this case, the staffing function in Theorem 8 is just sufficient to guarantee that all fluid enters service immediately upon arrival (thus with 0 delay in the queue) and that the system is CL for all t (the service capacity is fully occupied, i.e., B(t)=s(t)). This scenario corresponds to the heavy-traffic QED system regime.
Remark 9
(General initial conditions or no delay)
Theorem 8 is based on starting empty. However, it is possible to stabilize delays with arbitrary initial conditions. We present the details in Appendix H of [24]. We can also achieve the minimum staffing level so that there is no delay at all by simply staffing at the fluid content B(t) in the underloaded regime. These two variants may involve having an atom of initial fluid content enter service at time 0, so that we leave the smooth framework.
11 Proofs of the main results
Proof of Theorem 3
We establish the different results in turn:
(a) (Rate of growth) Consider an interval [t,t+δ] that is overloaded. If no fluid enters service during this interval, i.e., if b(s,0)=0 for t≤s≤t+δ, then the waiting time of a quantum of fluid at the front of the queue will increase with rate 1, i.e., w(t+δ)=w(t)+δ, provided that quantum does not abandon. Hence, we have the claimed bound on the rate of growth: w(t+u)≤w(t)+u for all t≥0 and u≥0 with t+u≤T. A more formal argument follows from (5) in Assumption 6.
(b) (Characterization) However, we will have w(t+δ)<w(t)+δ if b(t,0)>0 because the FCFS service discipline implies that the queue is being eaten away from the head. In other words, fluid is being transported from the queue to the service facility from the right boundary of q(t,x). Therefore,

where ϵ(t,δ) is the amount of boundary waiting time w(t) that is pushed back (eaten up) by b(t,0) from t to t+δ, see Fig. 6. (Note that δ>0 and ϵ(t,δ)≥0.) To determine ϵ(t,δ), we apply (30), with (31). We will bound ϵ(t,δ) in (51) below.
(c) (Controlling the abandonment term) We will show that the abandonment term A(t,t+δ) in (30) is asymptotically negligible, so that it can be ignored when computing the derivative, but we use it to establish Lipschitz continuity. Even though A(t,t+δ) is somewhat complicated, we can easily bound it above. Moreover, we can do so uniformly in t over the entire interval [0,T]. First let w ↑≡sup{w(t):0≤t≤T}. We necessarily have w ↑≤w(0)+T<∞ by virtue of the bound on the growth rate growth determined above. Next let \(h_{F}^{\uparrow} \equiv\sup{\{h_{F}(x): 0 \le x \le w^{\uparrow}\}}\) which necessarily is finite, since f∈ℂ p and \(\bar{F} (w^{\uparrow}) > 0\); and let \(\tilde{q}^{\uparrow} \equiv\sup{\{\tilde{q} (t, x): 0 \le x \le w^{\uparrow}\}}\), which again necessarily is finite because \(\tilde{q}(t, \cdot) \in \mathbb {C}_{p}\). We thus have the bound
for 0≤t≤t+δ≤T, where \(C_{1} \equiv h_{F}^{\uparrow}\tilde{q}^{\uparrow} w^{\uparrow}\), because ϵ(t,δ)≤w ↑ δ.
(d) (Lipschitz continuity) By (49), we can show that w is Lipschitz continuous by showing that ϵ(t,δ)≤Cδ for some constant C. Recall that b(⋅,0) is an element of \(\mathbb {D}\) by Theorem 2. Hence, ∥b(⋅,0)∥ T <∞, so that there exists a constant C 2 such that E(t+δ)−E(t)≤C 2 δ for 0≤t≤t+δ≤T. Together with (50), that implies that the integral \(I(t, w(t), \tilde{q}, \delta)\) is bounded above by Cδ for 0≤t≤t+δ≤T, where C≡C 1+C 2. Since the integrand of I is bounded below by c>0 by virtue of Assumption 10,
for 0≤t≤t+δ≤T, so that indeed
as claimed.
(e) (The derivative) Since w is Lipschitz continuous, w necessarily is differentiable a.e., but we will establish a stronger result. Given that ϵ(t,δ)=cδ+o(δ) as δ↓0, from the first inequality in (50) we see that A(t,t+δ)=O(δ 2)+o(δ 2), so that the abandonment term can be ignored when we consider the derivative. Together with (30) and (31), that implies that a right derivative of w exists at t with value in (32). The convergence as δ↓0 in the definition of that right derivative will be uniform over a neighborhood of t if \(\tilde{q}(t, x)\) is continuous function of x at x=w(t), but not otherwise.
To show (33) is similar. We consider an interval [t−δ,t] that is overloaded. Similarly, we have

and
where
and

A closer look at K implies

where the first equality follows from (52) and fundamental evolution equations, the second equality holds by change of variable. It is easy to see that K=o(δ) as δ↓0. Therefore, together with (53), that implies that a left derivative of w exists at t with value in (33).
The stronger differentiability conclusion depends on the discontinuities of \(\tilde{q} (t,x)\). From Proposition 6, all discontinuity points lie on finitely many 45 degree lines in the upper right quadrant [0,∞)×[0,∞); i.e., in the set \(\{(t,x): x = t +c \mbox{ and } c \in \mathcal {S}\}\) where \(\mathcal {S}\) contains c=0 and the finite set of discontinuities of λ for c<0 and the finite subset of discontinuities of q(0,⋅) for c>0. Since w(t+u)≤w(t)+u for 0≤t≤t+u≤T, the trajectory of \(\tilde{q} (t, w(t))\) crosses over each of these lines at most once. Moreover, it stays on each line for at most a finite interval. If the trajectory immediately crosses over the line, then the crossing time t constitutes the sole discontinuity point for w′ associated with that line. If the trajectory stays on the line for an interval, then the two endpoints constitute discontinuity points for w′ associated with that line.
(f) (Existence of a solution) The solution can be constructed by considering the successive intervals between discontinuity points and piecing together the solutions. The function Ψ in (32) is continuous in each continuity interval. Hence, existence follows from Peano’s theorem; see Sect. 2.6 of [35]. We apply Assumption 9 to ensure that w(0)<∞.
(g) (Uniqueness of a solution) Under extra regularity conditions, the function Ψ in (32) will be locally Lipschitz on each continuity interval of w′, so that each piece constructed in the existence argument above will be unique, by virtue of the classical Picard–Lindelöf theorem; e.g., Theorem 2.2 of [35]. Specifically, it suffices to assume that λ and q(0,⋅) (already assumed to be in ℂ p ) are differentiable on the subintervals where they are continuous with derivatives in ℂ p over these subintervals.
However, we can actually prove uniqueness without resorting to extra assumptions. To do so, we exploit the special structure of the ODE in (32). By (29) in Corollary 3, q(t,w(t)−) in the denominator or (32) takes one of two forms, depending on whether w(t)≤t or not. Our proof applies to both cases in the same way, so we only consider one case: we suppose that w(t)≤t. Then \(q(t, w(t)-) = \lambda((t - w(t))-)\bar{F}(w(t))\). Then ODE (32) implies that

Now suppose there is another function \(\tilde{w}\) that also satisfies ODE (32) with \(\tilde{w}(t_{1})=0\). Then, by the same reasoning, we get
Equations (54) and (55) imply that
Now suppose function w and \(\tilde{w}\) are different. Since \(w(t_{1})=\tilde{w}(t_{1})=0\), let \(\tilde{t}\equiv\inf\{{t>t_{1}}:w(t)\neq \tilde{w}(t)\}\), which implies that \(w'(\tilde{t})\neq\tilde {w}'(\tilde{t})\). Without loss of generality suppose that \(w'(\tilde{t})<\tilde{w}'(\tilde{t})\); hence there exists a δ>0 such that \(w(t)<\tilde{w}(t)\) for all \(\tilde{t}<t\leq\tilde{t}+\delta\). Then we have \(1/\bar{F}(w(t))<1/\bar{F}(\tilde{w}(t))\) for all \(\tilde{t}<t\leq\tilde{t}+\delta\) and \(\tilde{t}+\delta-\tilde{w}(\tilde{t}+\delta)<\tilde{t}+\delta-w(\tilde{t}+\delta)\). Therefore, (56) implies that
which is a contradiction. Hence the solution to ODE (32) must be unique. □
Proof of Theorem 5
To show that the two equations in (37) are equivalent, make the change of variables s≡t−w(t). Then the first equation gives v(s)=w(t)=w(s+w(t))=w(s+v(s)), which is the second equation. The other direction is similar.
For a given w, we shall do three things: (i) construct v given the first equation in (37), (ii) show that this construction gives a function v that is right-continuous and has limits from the left, and (iii) show that the construction in (i) is the unique one that satisfies (ii).
For an arbitrary t, we draw a 45-degree ray starting from point (t,0): L(s)=s−t, s≥t. Let v(t) be the largest t w such that L(t w )=w(t w ), as shown in Fig. 5. We first show that there necessarily exists at least one time t w ≥t such that L(t w )=w(t w ). If w(t)=0, then t w =t is a solution. Otherwise, we have w(t)>0=L(t), and w starts above the line L at time t. By Theorem 3, w is a continuous function. In general, we could have w(t)>L(t) for all t, but then we would have v(t)=∞. Since v(t)<∞, there necessarily is a time t w such that L(t w )=w(t w ).
By Theorem 3, w′(t)≤1. Therefore, once L(t w )=w(t w ) for the first time, it either stays there or leaves, never to return. In other words, there are two cases: First, as always occurs if w′(t w )<1, there may be a unique t w ≥t such that L(t w )=w(t w ). Second, there may exist an interval I≡[t 1,t 2] such that L(t)=w(t) for t∈I, i.e., L(t 1)=w(t 1) and w′(t)=1 for t∈I; see Fig. 5. In the first case, we let v(t)≡t w ; in the second case, we let v(t)≡w(t w ) where t w ≡inf{s>t 1:L(s)≠w(s)}. That completes our construction.
Next we show right-continuity. For any ϵ>0, our construction shows that it is possible to choose δ>0 sufficiently small that v(t+δ)=w(t w +δ+ϵ) such that w(t w +δ+ϵ)−w(t w )=ϵ, where ϵ≡ϵ(t,δ), as shown in Fig. 7. Our construction implies that

for some \(t_{w}\leq\hat{t} \leq t_{w}+\delta+ \epsilon\) and \(w'(\hat{t})<1\), which implies that

Therefore, as δ→0,

by the continuity of w. Therefore, v is right-continuous. Similarly, we can show that v has limits from the left.
It is evident that, by this construction, we have ensured that v is right-continuous with left limits and unique. Moreover, v is discontinuous at t if and only if we are in the second case with an interval of solutions. □
Proof of Theorem 6
For δ>0, the second equation in (37) yields

where ϵ(t,δ)≡v(t+δ)−v(t)+δ. Simple algebra implies that

Letting δ↓0, we obtain

where the second equality holds since right-continuity of v implies that ϵ(t,δ)→0 as δ→0, the third equality follows from ODE (32), the fourth equality follows from the second equation in (37), the last equality holds because the system being overloaded at time t+v(t) implies that \(\tilde{q}(t+v(t),v(t)) =q(t,0)\bar{F}(v(t))=\lambda(t)\bar{F}(v(t))\). The similar argument applies to the left derivative with (v(t)−v(t−δ))/δ when t is a continuity point of v.
By Theorem 5, v is continuous under the extra condition that b(t,0)>0 for all t. That clearly makes the right derivative finite for all t. Hence, v is differentiable wherever Φ is continuous. We can now exploit Theorem 3 and its proof. Since b(t,0)>0 for all t, there will be a one-to-one correspondence between the finitely many points where Ψ in (32) is discontinuous and the points where Φ is discontinuous. Now we have the relations (for the right derivatives everywhere)
with the denominators positive in both cases. Directly, we can establish existence and uniqueness of a solution to the ODE by the same reasoning as used for ODE (32) for w. □
12 Conclusions
In this paper we have characterized all the standard performance functions for the G t /GI/s t +GI fluid model. Our results were obtained under two important regularity conditions: (i) Assumption 2, requiring that we have a smooth model, and (ii) Assumption 7, requiring that there be only finitely many switches between overloaded (OL) and underloaded (UL) intervals in finite time. There also is a restriction on the service distribution in Assumption 8 in order to guarantee that the fixed-point equation (18) for the rate of flow from queue into service, b(t,0), has a unique solution that can be computed iteratively. It suffices for either (i) the service hazard function h G to be bounded or (ii) the system to have started empty at some time in the (finite) past; see Sect. 6. Additional regularity conditions were imposed in Sect. 7 to obtain results for the waiting times.
For M service, the relatively simple algorithm primarily requires solving the ODE for the BWT w in Theorem 3 and the equation for the PWT v in Theorem 5 during each OL interval. For non-exponential service, in addition we must solve the fixed-point equation (18) for the flow rate into service b(t,0), which is needed to determine the full service content density b(t,x). The algorithm is summarized in Sect. 8. We characterized the model, as just reviewed, under the assumption that the staffing function s is feasible, but in Theorem 7 we also characterized the minimum feasible staffing function greater than or equal to any given staffing function, provided that it is not changed prior to the first infeasibility time. In Sect. 10 we showed that we can construct a staffing function to stabilize the potential waiting time v at any desired target v ∗>0.
The fluid model is well defined directly, but it is intended to serve as an approximation for large-scale many-server queueing systems. We performed extensive simulation experiments to confirm that the fluid model can provide a useful approximation for such stochastic queueing systems. One of these experiments is described in Sect. 2; others are described in [24]. The simulation results show that, first, the fluid approximation is essentially exact for very large queueing systems and, second, it can be effective as an approximation for mean values even when the scale is not too large; e.g., the number of servers might be only 20. The approximation tends to be more accurate when the system is either overloaded or underloaded, rather than critically loaded, as illustrated by Fig. 3.
The results here even contribute to our understanding of the stationary G/GI/s+GI fluid model introduced in [37]. For the special case of the G/M/s+GI fluid model, building on the present paper, in [21] we prove that the time-dependent performance of the fluid model converges to that steady-state performance as time evolves for any finite initial condition. Moreover, we provide bounds on the rate of convergence. In [21] we also establish convergence to a periodic steady state for periodic models and we establish asymptotic loss of memory (ALOM) for more general time-varying models.
There are many directions for future research. (i) It remains to consider alternative approaches to obtaining feasible staffing functions. The method in Sect. 9 detects any infeasibility of a candidate staffing function and removes the problem by increasing the staffing after the violation point. Alternative methods could modify the entire staffing function, aiming to achieve minimum cost subject to constraints. (ii) It remains to establish existence, uniqueness and algorithm results for the more general model in which many of the regularity conditions imposed here are relaxed. (iii) It remains to extend the model to represented more complicated service systems with multiple service pools and multiple customer classes. Building on the present paper, a first step has been made for single-class networks of queues with time-varying Markovian routing among the queues in [20]. (iv) Finally, it remains to develop alternative approximations and many-server heavy-traffic limits for G t /GI/s t +GI systems that tend to be nearly critically loaded at all times, instead of switching back and forth between OL and UL intervals.
References
Abate, J., Whitt, W.: The Fourier-series method for inverting transforms of probability distributions. Queueing Syst. 10, 5–88 (1992)
Abate, J., Whitt, W.: Numerical inversion of Laplace transforms of probability distributions. ORSA J. Comput. 7, 36–43 (1995)
Aksin, Z., Armony, M., Mehrotra, V.: The modern call center: a multi-disciplinary perspective on operations management research. Prod. Oper. Manag. 16, 665–688 (2007)
Asmussen, S.: Applied Probability and Queues., second edn. Springer, New York (2003)
Bassamboo, A., Randhawa, R.S.: On the accuracy of fluid models for capacity sizing in queueing systems with impatient customers. Oper. Res. 58, 1398–1413 (2010)
Billingsley, P.: Convergence of Probability Measures. Wiley, New York (1968)
Billingsley, P.: Convergence of Probability Measures., second edn. Wiley, New York (1999)
Brown, L., Gans, N., Mandelbaum, A., Sakov, A., Shen, H., Zeltyn, S., Zhao, L.: Statistical analysis of a telephone call center: a queueing-science perspective. J. Am. Stat. Assoc. 100, 36–50 (2005)
Davis, J.L., Massey, W.A., Whitt, W.: Sensitivity to the service-time distribution in the nonstationary Erlang loss model. Manag. Sci. 41, 1107–1116 (1995)
Eick, S.G., Massey, W.A., Whitt, W.: The physics of the M t /G/∞ queue. Oper. Res. 41, 731–742 (1993)
Eick, S.G., Massey, W.A., Whitt, W.: M t /G/∞ queues with sinusoidal arrival rates. Manag. Sci. 39, 241–252 (1993)
Feldman, Z., Mandelbaum, A., Massey, W.A., Whitt, W.: Staffing of time-varying queues to achieve time-stable performance. Manag. Sci. 54, 324–338 (2008)
Garnett, O., Mandelbaum, A., Reiman, M.I.: Designing a call center with impatient customers. Manuf. Serv. Oper. Manag. 4, 208–227 (2002)
Green, L.V., Kolesar, P.J., Whitt, W.: Coping with time-varying demand when setting staffing requirements for a service system. Prod. Oper. Manag. 16, 13–39 (2007)
Hall, R.W.: Queueing Methods for Services and Manufacturing. Prentice Hall, Englewood Cliffs (1991)
Ibrahim, R., Whitt, W.: Wait-time predictors for customer service systems with time-varying demand and capacity. Oper. Res. 59, 1106–1118 (2011). http://www.columbia.edu/~ww2040/allpapers.html
Jennings, O.B., Mandelbaum, A., Massey, W.A., Whitt, W.: Server staffing to meet time-varying demand. Manag. Sci. 42, 1383–1394 (1996)
Kang, W., Ramanan, K.: Fluid limits of many-server queues with reneging. Ann. Appl. Probab. 20, 2204–2260 (2010)
Kaspi, H., Ramanan, K.: Law of large numbers limits for many-server queues. Ann. Appl. Probab. 21, 33–114 (2011)
Liu, Y., Whitt, W.: A network of time-varying many-server fluid queues with customer abandonment. Oper. Res. 59, 835–846 (2011)
Liu, Y., Whitt, W.: Large-time asymptotics for the G t /M t /s t +GI t many-server fluid queue with abandonment. Queueing Syst. 59, 835–846 (2011)
Liu, Y., Whitt, W.: Many-server heavy-traffic limit for queues with time-varying parameters. Columbia University, NY (2011). http://www.columbia.edu/~ww2040/allpapers.html
Liu, Y., Whitt, W.: A many-server fluid limit for the G t /GI/s t +GI queueing model experiencing periods of overloading. Columbia University, NY (2011). http://www.columbia.edu/~ww2040/allpapers.html
Liu, Y., Whitt, W.: The G t /GI/s t +GI many-server fluid queue: longer online version with appendix. http://www.columbia.edu/ww2040/allpapers.html
Mandelbaum, A., Zeltyn, S.: The impact of customers patience on delay and abandonment: some empirically-driven experiments with the M/M/n+G queue. OR Spektrum 26, 377–411 (2004)
Massey, W.A., Whitt, W.: Networks of infinite-server queues with nonstationary Poisson input. Queueing Syst. 13, 183–250 (1993)
Mandelbaum, A., Massey, W.A., Reiman, M.I.: Strong approximations for Markovian service networks. Queueing Syst. 30, 149–201 (1998)
Mandelbaum, A., Massey, W.A., Reiman, M.I., Rider, B.: Time varying multiserver queues with abandonments and retrials. In: Key, P., Smith, D. (eds.) Proceedings of the 16th International Teletraffic Congress (1999)
Mandelbaum, A., Massey, W.A., Reiman, M.I., Stolyar, A.: Waiting time asymptotics for time varying multiserver queues with abandonment and retrials. In: Proceedings of the 37 Annual Allerton Conference on Communication, Control and Computing, Allerton, IL, pp. 1095–1104 (1999)
Newell, G.F.: Applications of Queueing Theory, second edn. Chapman & Hall, London (1982)
Pang, G., Whitt, W.: Two-parameter heavy-traffic limits for infinite-server queues. Queueing Syst. 65, 325–364 (2010)
Prabhu, N.U.: Stochastic Storage Processes: Queues, Insurance Risk, Dams, and Data Communication, second edn. Springer, New York (1998)
Reed, J., Talreja, R.: Distribution-Valued Heavy-Traffic Limits for the G/GI/∞ Queue. New York University, New York (2009)
Talreja, R., Whitt, W.: Heavy-traffic limits for waiting times in many-server queues with abandonments. Ann. Appl. Probab. 19, 2137–2175 (2009)
Teschl, G.: Ordinary differential equations and dynamical systems. Universität Wien (2009). Available online: www.mat.univie.ac.at/~gerald/ftp/book-ode/ode.pdf
Whitt, W.: Engineering solution of a basic call-center model. Manag. Sci. 51, 221–235 (2005)
Whitt, W.: Fluid models for multiserver queues with abandonments. Oper. Res. 54, 37–54 (2006)
Yom-Tov, G., Mandelbaum, A.: The Erlang-R queue: time-varying QED queues with re-entrant customers in support of healthcare staffing. Working paper, the Technion, Israel (2010)
Zeltyn, S., Mandelbaum, A.: Call centers with impatient customers: many-server asymptotics of the M/M/n+G queue. Queueing Syst. 51, 361–402 (2005)
Acknowledgements
This research was supported by NSF grants DMI 0457095, CMMI 0948190 and CMMI 1066372.
Open Access
This article is distributed under the terms of the Creative Commons Attribution License which permits any use, distribution, and reproduction in any medium, provided the original author(s) and the source are credited.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 2.0 International License (https://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
About this article
Cite this article
Liu, Y., Whitt, W. The G t /GI/s t +GI many-server fluid queue. Queueing Syst 71, 405–444 (2012). https://doi.org/10.1007/s11134-012-9291-0
Received:
Revised:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11134-012-9291-0
Keywords
- Queues with time-varying arrivals
- Nonstationary queues
- Transient behavior
- Many-server queues
- Deterministic fluid model
- Customer abandonment
- Non-Markovian queues